基于三维Lorenz混沌系统的数字图像水印算法

康钦清（湖南涉外经济学院信息科学与工程学院,长沙410205）

基于三维Lorenz混沌系统的数字图像水印算法

康钦清
（湖南涉外经济学院信息科学与工程学院,长沙410205）

摘要：数字水印技术是知识产权保护和数字多媒体防伪的有效手段。分析比较数字图像水印算法中常见的混沌系统，选取三维Lorenz混沌系统产生的混沌序列对数字水印信息进行加密处理，增强水印信号的鲁棒性。水印图像的嵌入选用三级小波分解的系数，均衡不可见性和鲁棒性。水印图像的提取需要原始载体图像。

关键字：数字水印;混沌;Lorenz混沌系统;小波分解

1引言

计算机网络技术的发展，带来了数字多媒体产品（如图像、音频、视频、文本信息等）的广泛传播。便捷的同时带来严重的安全问题，如数字多媒体产品的版权侵犯、非法拷贝和篡改。数字水印技术成为解决这一问题的有效方法之一。数字水印技术就是将具有特定意义的标记（水印），利用数字嵌入的方法隐藏在数字图像、声音、文档、图书和视频等数字产品中，用以证明创作者对其作品的所有权，并作为鉴定、起诉非法侵权的证据，同时通过对水印的检测和分析来保证数字信息的完整可靠性，从而成为知识产权保护和数字多媒体防伪的有效手段[1]。̓̓

数字水印技术按水印特性分为可见水印、不可见易碎性水印、不可见稳健性水印。本文研究的是不可见稳健性水印。不可见稳健性水印的特性有：（1）水印不可感知性：嵌入的水印信息不影响原始载体图像的视觉效果，不能用统计方法恢复出水印，只能用专门的检测器检测或提取水印；（2）鲁棒性：嵌入水印信息的载体图像经过基本图像处理技术或被恶意攻击后仍能检测或提取出水印信息。̓̓

数字水印技术按嵌入位置还可以分为空域数字水印技术和变换域数字水印技术。空域数字水印技术直接对像素值进行处理，算法操作简单，水印容量大，可嵌入的信息多，但算法的鲁棒性不理想，抵抗基本图像处理能力差；变换域数字水印技术就是将空域转换到其他的变换域来进行水印的嵌入。此类方法鲁棒性好，但水印容量较空域要低。̓̓

本文利用Lorenz混沌系统产生三维混沌序列，对水印图像进行预处理，借助Lorenz混沌系统密钥空间大，增强水印信号的鲁棒性。由于人眼对小波分解高频系数敏感性较低，对低频系数较为敏感。为了保证嵌入的水印信息既具有良好的不可见性，又可以有较好的鲁棒性，本文采用文献[2]将载体图像三级小波分解，把预处理后的水印信号嵌入水平方向上的高频系数的位置。实验结果显示，水印信号解决了鲁棒性与不可见性之间的矛盾。

2Lorenz混沌系统

2.1混沌的定义

混沌是一个完全确定的系统中出现的一类类随机过程的现象，是有序与无序的统一，确定性与随机性的统一[3]。这种过程非周期、不收敛但有界，并且对初始状态具有极其敏感的依赖性，即初始状态只有微小差别的两个同构混沌系统在较短时间后就会产生两组完全不同的、互不相关的混沌序列值。

2.2常见的混沌系统̓̓

越来越多的人开展了对混沌系统的研究。在数字水印技术中，常见使用的混沌系统有以下几类：̓̓

简单常见的一类一维混沌系统是Logistic映射，其定义如下[4]： ̓

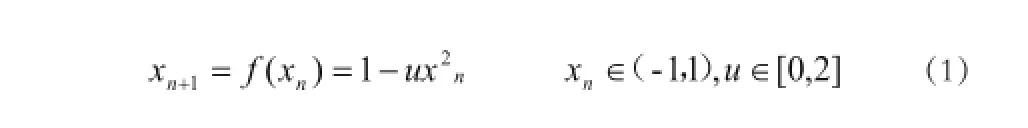
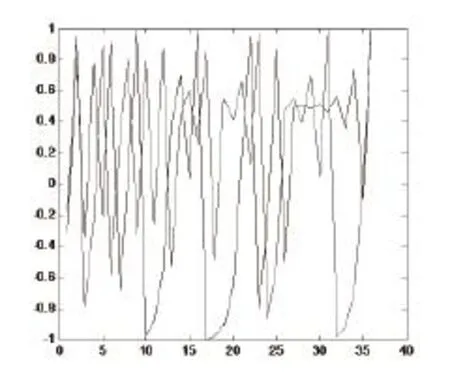
图1初始值相差0.001的两个混沌序列

随着计算机技术的发展，一维混沌系统的使用安全性难以保障，因此二维混沌系统得以发展。文献[5]采用二维Logistic映射。

。只有给定密码和控制参数产生的混沌序列才能生成正确的置乱坐标，使图像还原，大大增强了其安全性。

文献[6]提出混沌信号的质量是加密效果的关键。低维混沌系统有被预测风险。文中给出的三维Lorenz混沌系统结构较一维、二维混沌系统更为复杂，系统变量和参数有多个，系统变量的时间序列更加无规律性，不可预测。可对多个系统变量进行处理产生序列密码，可提供的密钥空间大大增加。三维混沌系统Lorenz系统的动力学方程为̓̓

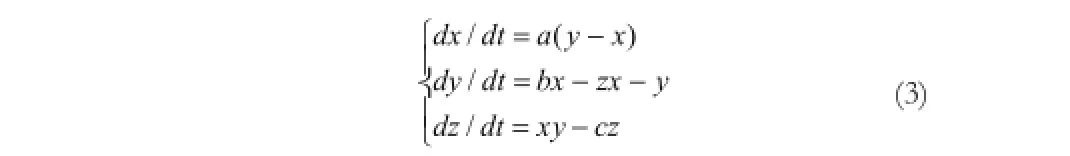
其中，a,b,c为系统参数，当a=10，c=8/3，b=28时，系统进入混沌状态。对于初始条件（x0,y0,z0），可得到三维混沌序列。初始参数和系统变量初值可作为密钥。本文选择三维Lorenz混沌系统产生的混沌序列对数字水印信息进行预处理，增强水印信号的鲁棒性。

2.3混沌系统在数字水印技术中的应用̓̓

文献[7]归纳混沌理论在数字水印的应用分为混沌序列数字水印、混沌映射数字水印和混沌系统数字水印。其中依靠混沌序列生成水印或者加密水印的混沌序列数字水印是研究热点。混沌序列数字水印的使用有三种常见方式：一类是单混沌序列水印。这种方式生成的水印属于无意义水印。无意义水印是指水印信息没有具体含义，只用于检测嵌入水印的宿主对象是否被篡改。文献[4]采用Logistic混沌系统产生的混沌序列进行适当截取生成二值序列作为无意义数字水印信号，嵌入到载体图像中。与扩频序列产生的伪随机信号相比，混沌序列以初值敏感性、获得更好的安全性。二值化处理后的混沌系列保密性增强，具备了数字水印信号的不可逆性。但在遭受有意或无意攻击后，混沌序列的正确检测难以实现，算法鲁棒性差。̓̓

一类是混沌置乱水印。嵌入载体图像中的水印信息为有意义水印。有意义水印包括徽章、标志和二进制小图像等下。有意义水印在版权证明上较无意义水印更具有直观性和可验证性。利用混沌序列对水印进行置乱后再嵌入到载体图像中，提取水印时，先照算法还原水印，再利用混沌序列还原水印。文献[5]利用二维Logistic混沌映射置乱加密方法进行水印预处理来加强水印信号的鲁棒性。此类方法优点是攻击者不知道混沌方程的初始值和方程参数无法提取正确的水印。

还有一类是双混沌序列水印。嵌入水印时，利用一个混沌序列对水印对象进行置乱，另一个混沌序列确定水印嵌入的位置。这类方法是三种方法中安全性最高的，缺点是运算量太大，有些情况下解决不了抗攻击能力对水印嵌入算法的依赖。

本文均衡安全性与运算量的要求，采用混沌置乱水印的方法。选择三维Lorenz混沌系统产生的混沌序列对数字水印信息进行置乱，增强水印信号的鲁棒性。

3数字图像水印的实现

3.1水印嵌入

本算法的基本思想用三维Lorenz混沌系统生成的混沌序列对水印图像进行置乱加密处理，然后对原始载体图像进行3级小波分解，将置乱后的水印图像嵌入到第3级小波分解的水平高频和垂直高频子带绝对值较大系数中，最后进行逆小波变换得到含水印的载体图像。具体实施步骤如下

步骤2对原始载体图像进行3级小波分解，在第3级的水平高频分量子带LH3和垂直高频分量子带HL3中，找出绝对值较大的系数作为水印的嵌入位置。

步骤3按照式嵌入水印图像

步骤4把所有小波系数进行小波逆变换，得到含水印的载体图像。

3.3水印提取

水印提取是水印嵌入的逆过程。本算法是非盲水印检测算法，提取过程中需要原始载体图像。将原始载体图像与待检测图像小波系数比较，得到加密后水印图像，最后根据密钥，对提取的水印信息进行解密。具体提取步骤如下。

步骤3解密。用密钥生成的三维Lorenz混沌序列对杂乱无章的水印图像进行解密，恢复出水印图像。

为客观评价提取水印与原始水印的相似程度，采用以下计算公式(6)-(8)：

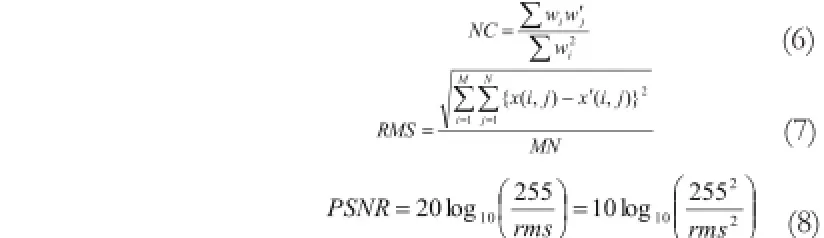
4实验结果及分析

本文采用512*512的lena作为原始图像，水印图像采用64*64大小的二值图像，三维Lorenz系统的系统参数a=10，c=8/3，b=28和初始条件(x0,y0,z0)=(12.1052,7.8090,35.8921)，小波分解选用Haar小波基，图2给出了仿真结果。

在无攻击条件下，水印图像可以完整提取出来。表1给出不同图像处理PSNR和提取的水印的NC值。

5结论

本文给出了基于Lorenz混沌系统的数字图像水印算法。三维Lorenz混沌系统结构较一维、二维混沌系统更为复杂，系统变量和参数有多个，系统变量的时间序列更加无规律性，不可预测。三维Lorenz混沌系统产生的混沌序列对数字水印信息进行置乱，增强水印信号的鲁棒性。

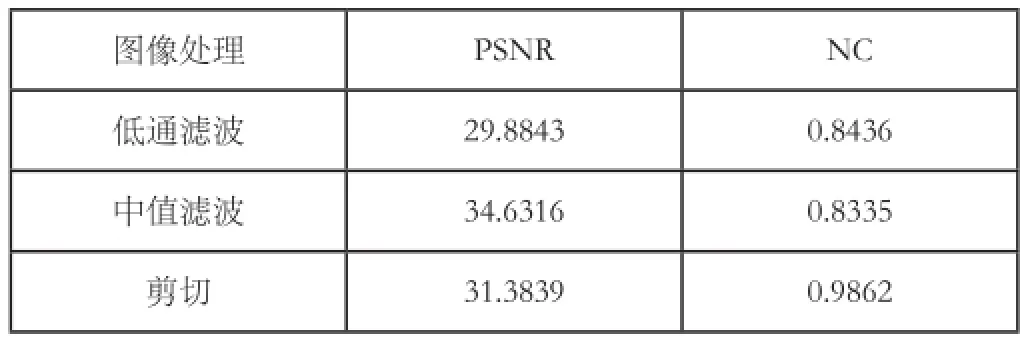
表1不同图像处理PSNR和提取的水印的NC

参考文献:

[1]孙圣和,陆哲明,牛夏牧.数字水印技术及应用(第1版)[M].科学出版社,2004:32-37.

[2]陈河山,吕珍珍,罗伟.一个基于离散混沌加密的数字水印算法[J].计算机科学,2014,12(41):48-52.

[3]吕金虎,陆君安,陈士华.混沌时间序列分析及其应用(第1版) [M].武汉：武汉大学出版社,2002:1-10.

[4]纪震,李慧慧,肖薇薇.基于混沌序列的数字水印信号研究[J].电子学报,2004,7(32):1132-1134.

[5]陈善学,彭娟,李方伟.基于二维Logistic混沌映射的DWT数字水印算法[J].重庆邮电大学学报(自然科学版),2012,4(24):495-500.

[6]叶菲,罗景青.基于Lorenz混沌加密的彩色图像水印算法[J].计算机应用与软件,2008,12(25):278-280.

[7]刘竹松,陈平华,刘怡俊.混沌数字水印技术研究进展[J].计算机应用研究,2011,1(28):1-5.

项目支持：湖南涉外经济学院2011年度校级科研一般项目立项资助，项目编号： 201111

作者简介：康钦清（1982-），女，湖南邵阳人，硕士,讲师，主要研究方向：数字水印、信息安全。