有压输水管涵检修时的气液二相流瞬变研究
孟国强
(河北省南运河河务管理处,河北 沧州061001)
有压输水管涵检修时的气液二相流瞬变研究
孟国强
(河北省南运河河务管理处,河北 沧州061001)
结合wylie的自由气体离散模型,构建了分段低压输水系统因检修操作导致检修箱涵进气的瞬变流数学模型,并结合实例对计算结果进行了分析。该研究可以为长距离有压输水系统的设计和运行管理提供理论依据和技术支持,同时也为二相流的气泡模拟提供一种可供借鉴的思路和方法。
有压管涵;气液二相流;水力瞬变
随着经济的发展、人口的增长及城市进程的加快,人们对水资源的需求量越来越多,加之水资源时空分布不均,不同地区尤其一些大中型城市都出现了水资源短缺问题,而修建长距离调水工程是调节水资源时空分布不均,解决水资源供需矛盾的最有效、最直接的手段。其中有压管道输水因其响应快、无渗漏和蒸发等损失、可以保障水质安全等优点,得到了广泛应用。也正是因为有压管道输水的波速大、水力响应快,使得输水管道在工况转换时会产生剧烈的水力波动,严重时会影响输水安全,因此水力瞬变控制一直是有压输水系统设计和运行管理关注的重要问题。
以往人们对于有压管道的水力控制研究多集中在流量调节、事故停泵等工况方面,而对于关闸检修工况则关注不多。长距离有压输水系统常在管道沿线设置若干的检修井和检修闸,以备工程检修。在实施检修时,需要关闭检修闸门,使系统停水。因关闸检修所引起的水力瞬变过程是水力控制中需要重点关注的问题之一。长距离有压输水系统在检修时如果检修闸关闭过快,将导致瞬变过程更为剧烈,检修井后接管涵会出现局部的短暂脱空,空气会被吸入形成气泡,产生气液两相流,将使水力瞬变过程更为复杂,其控制难度也就更大。
对于有压管道气液两相瞬变流的研究兴起于20世纪60年代[1],主要有两种数学模型,一种是自由气体-液体离散模型[2],该方法将气泡限制在固定的截面上,而认为各气泡截面之间不含有气体,仍然采用固定的水击波速对瞬变流进行计算;另一种模型是气体释放模型[3],假定液体中的空气均匀的分布在整个区域上,在瞬变流的计算过程中需要根据压力及空穴率的变化采用变化的水击波速进行计算,同时可以考虑瞬变过程中的气体释放。这两种数学模型根据模拟的实际条件的不同有其各自的应用范围,在某些特殊的情况下,这两种数学模型可以相互结合,即在考虑变波速的情况下,在特殊断面建立气体-液体离散模型的内部边界,使得模拟更接近于实际情况。
本文根据长距离有压输水系统检修井处的水流连续方程推导了过渡过程中有压箱涵进气量的计算公式,并对气体在管道中的运动进行了模拟,并根据有压管道进气的实际情况,结合wylie的自由气体-液体离散模型,构建了分段低压输水系统因检修操作导致检修箱涵进气的瞬变流数学模型,并对计算结果进行了分析。本文的研究可以为有压输水系统的设计和运行管理提供理论依据和技术支持,同时也为二相流的气泡模拟提供一种可供借鉴的思路。
1 检修箱涵进气量的计算
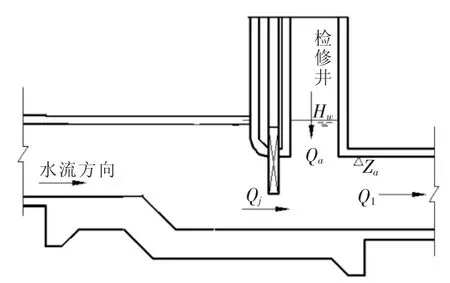
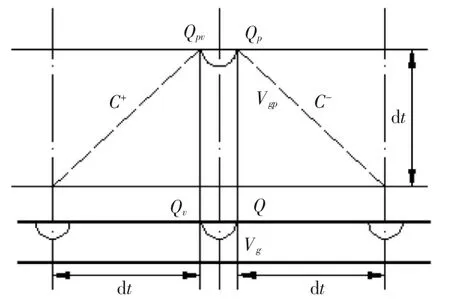
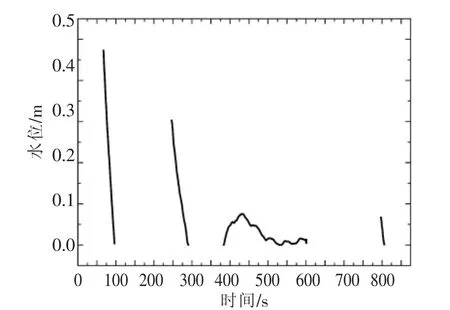
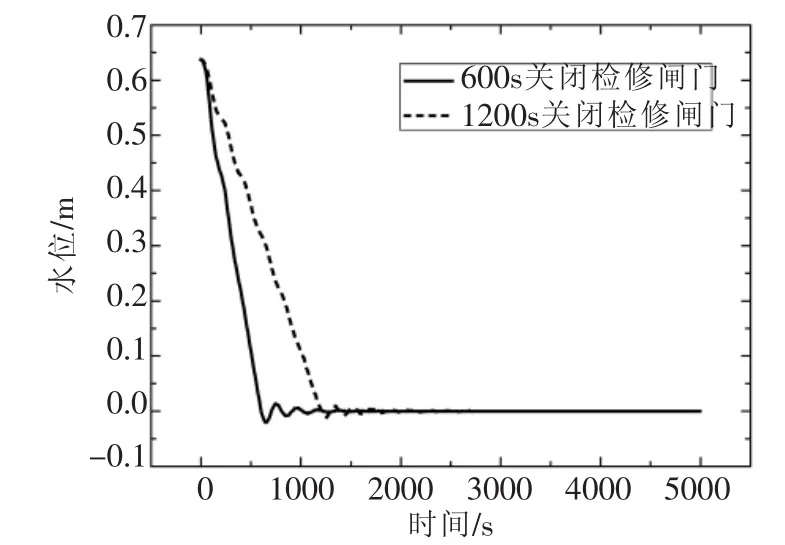
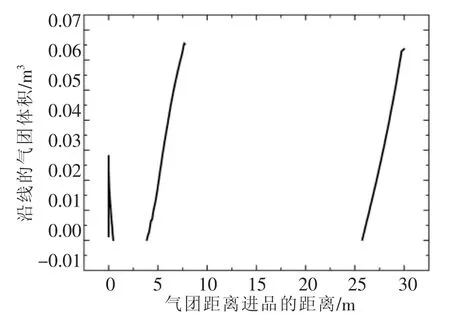
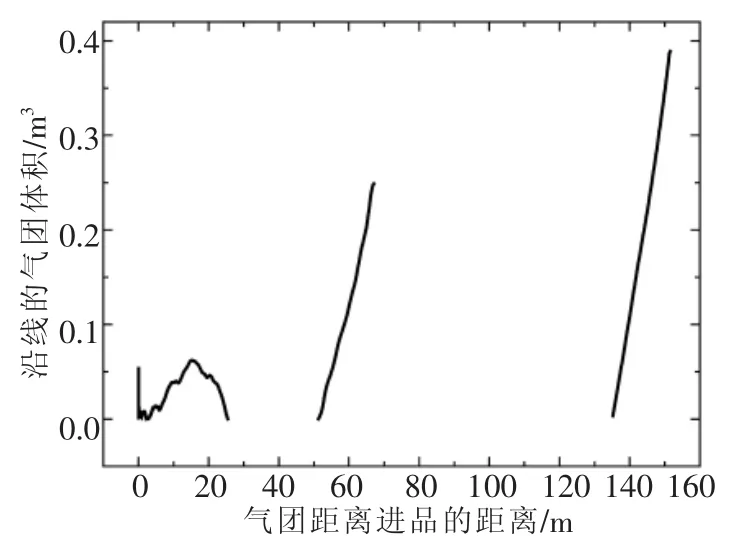
假定当检修井的水位小于检修井后接管顶高程时,而且过检修闸的流量小于检修井后接箱涵进口流量时,即Hw 根据检修井的连续方程,进入箱涵的空气流量为: 式中 Hw为检修井水位;Za为检修井后接管顶高程;Qj为过检修闸的流量;Q1为检修井后接箱涵进口流量。 检修箱涵进气示意图如图1。 图1 检修箱涵进气示意图 正负特征线方程为: 式中 CP,BP,CM,BM为特征线系数,由上一时步的已知量确定。 假定进入箱涵的气体为完善气体,由于空气的惯性力很小,可以忽略不计,气体一元流动的伯努里方程为: 式中 p为进入检修井的气体的压力;pa为大气压力;ρa为大气压下的空气密度,由于ρa密度很小,所以公式左边的第2项可以忽略不计,所以p≈pa,即进入检修井的空气压力在初始时刻可以看作是正常大气压。 将一个时步内,即ti+1-ti=Δt期间进入箱涵的空气视为一个气团[4],那么该气团在大气压下的体积为: 式中 Qa,i为ti时刻进入箱涵的空气流量。 在对气团的运动进行数学描述之前,先做如下假设: (1)气团在运动过程中始终视为一个整体,其质量始终保持不变。 (2)气团的体积变化遵循等温的完善的气体状态方程。 (3)根据检修时,检修井后接箱涵中的水流在闸门完全关闭之前流速较大,闸门完全关闭之后流速较小的特点,设定气团在闸门完全关闭之前随水流运行,其运动速度等于所在点的流速。在闸门完全关闭之后,所有的气团将停在管线当前的位置。 根据以上假定,在闸门完全关闭之前,任意时刻ti+1气团k在压力管道中的位置xk为: 式中 k为气团的编号;xk0为ti时刻气团所在的位置,在每一时步的计算过程中,为已知值,以箱涵进口为坐标原点;vk0为ti时刻气团的运动速度。 ti时刻气团的运动速度vk0需要根据气团k所在的位置xk0通过内差求得。假设气团k位于箱涵计算断面j和j+1之间,其位置坐标分别为xj和xj+1,断面j出口侧的流速为vj,2,断面j进口侧的流速为vi+1,1,那么气团k的运动速度vk0可用式(8)表示: 式(7)和式(8)联立可以求得气团k所在的位置坐标,从而可以对气团在有压箱涵中的运动进行描述。 如果在水中存有被截留的气团或是夹杂自由气泡,那么水击波速将变成时间和压力的函数,从而使得瞬变流的分析变得大为复杂。wylie的自由气体-液体离散模型[2]不把注意力集中在两相流的气泡动力学上,而是从宏观着眼来处理含有气团或自由气泡的瞬变流。该模型把气团限制相应的固定计算断面上,气团体积随压力的变化规律符合等温的完善气体状态方程,而断面与断面之间认为不存在气团,仍然采用固定波速。如果管道中有气团可能聚结的高位部分或是只有管系的一部分存在气团或自由气泡,那么这种假设就是合理的,所以该模型也适用于模拟本文的分段低压检修所造成的箱涵进气现象。 在计算得到ti+1时刻每一气团的位置xk后,就能计算断面j和j+1之间的箱涵中在该时刻的所有气团的量。 式中 V0,i为断面j和j+1之间的气团在大气压下的体积;V0,j+1即为ti+1时刻固定在j+1断面的气团在大气压下的体积。 根据等温的完善气体状态方程,有以下关系: 式中 Pa为大气压力;Pg为箱涵中的气团压力;Vj+1为压力Pg下的气团体积。 而气团压力与测压管水头的关系如下: 式中 γa为气体容重;HP为测压管水头;Z为该截面的管顶高程;Ha为气压计压头。 采用图2所示的矩形网格,其特征线的相容性方程如下: 图2 自由气体—液体离散模型 由断面处的连续方程可得以下关系式: 式中 QP和QPU分别为(t+dt)时刻的计算节点的来流和出流流量;Q和QU分别为t时刻计算节点的来流和出流流量;Vgp和Vg分别为(t+dt)和t时刻计算节点处气团的体积;φ为加权因子,将其引入是为了控制数值求解过程中的数值振荡,0.5≤φ≤1。 通过式(9)~式(14)联立即可求得瞬变过程中的含有气泡的有压箱涵的压力变化过程。 3孔并联有压输水系统如图3所示,由首端控制的流量经调节池进入有压箱涵,沿线设置有8个检修井,以1#~8#表示。其中2#、4#、6#、8#检修井通过设置连通孔实现了并联管段之间的水力连通,而并联输水单元在1#、3#、5#、7#检修井处则不连通。 此外在每座检修井内均设置有一个堰,其堰顶高程高于上游管涵的出口,可以在停水时将水体挡在上游管涵内,使未参与检修的管道不至于全部排空,可以避免大面积的排空和再运行时的充水。 图3 多孔并联有压输水系统计算概化 由于每段箱涵出口设有堰顶高于其出口的挡水堰。上述有压输水系统的正常检修操作程序是:先关闭箱涵上游的检修闸门,然后等到箱涵内的过渡过程停止,水体静止后,再关闭箱涵出口的检修闸门。由于双号检修闸设置有连通孔,因此检修操作并不影响非检修管道的正常输水。 在算例中,正常输水工况下,各管涵出口的挡水堰均为自有堰流的流态,计算时仅模拟了3#不连通检修闸门的关闭情况。当堰前水位低于堰顶高程时,保水堰前后水体断开,堰前堰后水体互不相关的波动,否则堰前堰后水体相连,按照自由堰流计算。 运行过程中的检修操作往往会引起剧烈的水力波动,这是因为运行过程中输水流量较大,而检修时,输水流量会在很短的时间内减为零,所以引起的过渡过程比较剧烈。如果检修闸关闭较为迅速,检修井后接箱涵会出现局部的短暂脱空,空气会被吸入形成气泡,产生气液两相流。利用本文所设计的数学模型对分段低压输水系统的检修操作进行模拟,其计算结果如下。 图4是不同关闸速度下检修井的水位波动,箱涵进口的顶高程为3.6m,关闸的总时间分别为600s和1200s,可以看出关闸的速度越快,检修井的水位波动就越剧烈,造成的检修井后接箱涵进口出现的短暂局部脱空程度就越大,从而进气量也就越大。图5和图6所示是不同关闸速度下的,检修过程中箱涵的进气过程。可以看出在过渡过程中,进气过程分为几个阶段,每次一般持续几十秒钟。1200s关闸时最大的进气流量为0.08m3/s,当关闸速度变快时,进气流量明显加大,在600s关闸时,最大的进气流量为0.47m3/s。 图7是不同关闸速度下箱涵进口的流速变化情况,可以看出在关闸的过程中进口的流速开始减小,当闸门全部关闭后,进口流速只是经过轻微的波动便稳定为零,所以数学模型中的假设,即“气团在闸门完全关闭之前随水流运动,其运动速度等于其所在点的流速。在闸门完全关闭之后,所有的气团将停在当前的位置”是合理的。 图4 不同关闸速度下检修井的水位波动 图5 检修闸1200s关闭,进入箱涵的空气流量过程 图6 检修闸600s关闭,进入箱涵的空气流量过程 图7 不同关闸速度下箱涵进口的流速 图8 检修闸1200s关闭,稳定后的气团分布 图9 检修闸600s关闭,稳定后的气团分布 图8和图9是不同关闸速度下瞬变流稳定后,沿线气团的分布情况,从中可以看出,关闸的速度越快,引起的水力瞬变就越剧烈,箱涵的进气量就越大,气团在管线的分布范围也就越大。1200s关闸检修的情况下,气团最远运动到距离管口30m处,沿线最大的气团体积为0.068m3,而在600s关闸检修的情况下,气团最远运动到距离管口151m处,沿线最大的气团体积为0.39m3。 由以上分析可以看出,有压输水系统在检修时如果检修闸关闭过快,将导致瞬变过程变得更为剧烈,检修井后接箱涵会出现局部的短暂脱空,空气会被吸入形成气泡,产生气液两相流。本文根据检修井处的水流连续方程推导了过渡过程中有压箱涵进气量的计算公式,并对气体在管道中的运动进行了模拟,并结合wylie的自由气体离散模型,构建了分段低压输水系统因检修操作导致检修箱涵进气的瞬变流数学模型,瞬变过程的加剧将导致箱涵进气量的增加,而气泡在箱涵中的运动距离也将更远,影响的范围也会增加。同时也证明了该方法可以较好地模拟分段低压输水系统因检修操作而导致箱涵进气的瞬变过程。可以为有压输水系统的设计和运行管理提供理论依据和技术支持,同时也为二相流的气泡模拟提供一种可供借鉴的思路和方法。 [1]郑源,刘德有,张健,等.有压输水管道系统气液两相瞬变流研究综述[J].河海大学学报(自然科学版),2002,30(6):21-25. [2]E.Benjamin Wylie ,Victor L.Streeter.Fluid transients[M].New York:McGraw-Hill International Book Co., 1978. [3]Fox J.A.Hydraulic Analysis of Unsteady Flow in Pipe Networks[M].London:The Macmilan Press LTD,1977. [4]杨开林,董兴林.水电站长输水道管流气泡动力特性研究[J].水利学报,1998(11):6-16. Study on gas-liquid two phase transient flow in the maintenance operation of pressure water transportation pipe culvert MENG Guo-qiang This paper combined with the free gas discrete model of wylie, constructed a transient flow mathematical model of an air inflow to the box culvert result in the maintenance operation of segmented low pressure water system,combining the instance and analysis of the calculation results.The research can provide the theory basis and technical support for the design and operation management of long distance water diversion system,also provide an ideas and methods that can be used for a bubble simulation of two phase flow. pressure pipe culvert; gas-liquid two phase flow; hydraulic transient TV222 B 1672-9900(2015)02-0027-05 2015-02-25 孟国强(1968-),男(汉族),河北海兴人,高级工程师,主要从事工程管理、引黄输水管理、调度与冰期输水研究、工程设计及审批等工作,(Tel)15303177222。
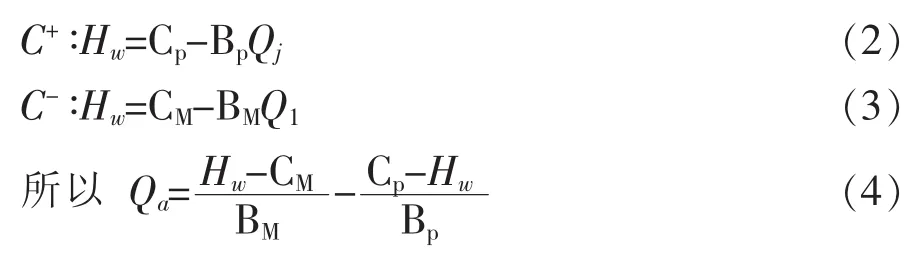

2 气体在箱涵中的运动

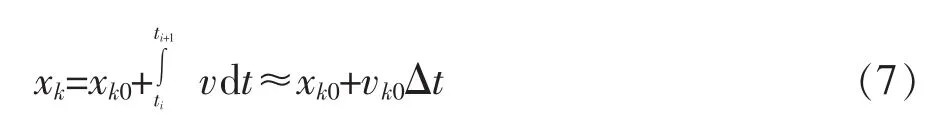
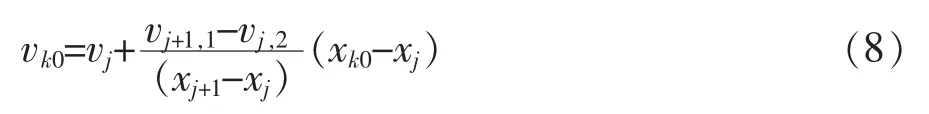
3 自由气体—液体离散模型




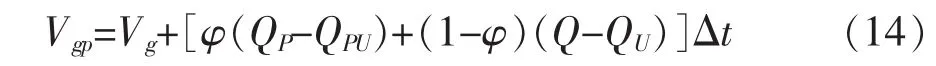
4 实例分析



5 结语
(Management Office of Nanyun River in Hebei Province,Cangzhou 061001,China)

