注入流体诱导应力场模拟计算

（1.中国石油大学（北京）非常规天然气研究院，北京 102249； 2.中国石油勘探开发研究院采油工程研究所，北京100083； 3.英国赫瑞·瓦特大学石油工程研究院，爱丁堡EH14 4AS； 4.中国石油勘探开发研究院廊坊分院压裂酸化技术服务中心，河北廊坊 065007）

（1.中国石油大学（北京）非常规天然气研究院，北京 102249； 2.中国石油勘探开发研究院采油工程研究所，北京100083； 3.英国赫瑞·瓦特大学石油工程研究院，爱丁堡EH14 4AS； 4.中国石油勘探开发研究院廊坊分院压裂酸化技术服务中心，河北廊坊 065007）

对油气井压裂改造时，向井眼内注入大量流体，井筒周围应力场重新分布，主要通过积分形式求解，过程繁杂，且对应力场的影响因素分析较少.利用拉氏变换，以流固耦合控制方程和应力平衡方程等为基础，结合注入流体诱导应力场的积分形式解，在定压条件下推导内、外边界拉氏变换解；利用Stephfest拉氏数值反演方法对变换解进行数值求解.数值模拟结果表明，切向应力场在最小水平主应力方向上变化较大，距离井壁越近，注入流体诱导的切向应力场值越大，随着距离增加，其值变小；在一定条件下（如地应力差较小），切向应力场发生反转，使得压裂裂缝转向.切向应力场与注入时间、流体黏度和地层渗透率等因素有关：延长注入时间、增加注入体积、较低的液体黏度和较高地层渗透率有利于使切向应力场增加，诱导切向应力场发生反转，有利于人工裂缝转向.

拉氏变换；注入流体；诱导应力场；数学模型；切向应力；径向应力

0 引言

油气井长期生产将导致地层孔隙压力下降，引起原地应力状态的改变.Elbel J L等采用流固耦合二维数值模型，研究前次裂缝周围孔隙压力随时间变化的影响［1］，证明长期生产逐渐改变地应力场，使得应力发生90°的反转.范学平等利用流固耦合二维数值模拟方法，研究油气井生产对地应力的影响［2］.张丁涌等利用多孔弹性模型估计孔隙压力衰竭对地应力的影响，结果表明孔隙压力减少使水平应力降低［3］.Weng X等研究生产诱导的地应力场对重复压裂裂缝延伸及压力响应的影响，如果生产诱导的应力场引起一条原始最小水平主应力方向的新裂缝起裂，那么其增加伴随快速增长的压力.原因是初始裂缝附近存在较高的应力梯度［4］，压力增加使初始裂缝张开，且一旦形成后，裂缝将消耗大部分注入流体，直到它到达初始裂缝端部为止；之后，与它垂直的裂缝开始增长.Sadegh Badakhshan Raz等给出天然气水合物（Gas Hydrate）气井生产过程中温度、孔隙压力、应变和应力分布的解析解，模拟生产对孔隙压力的应力场的影响［5］.Liu S等研究煤层气藏（CBM）生产诱导的应力场和割理渗透率的变化规律，结果表明气藏压力减少引起水平应力场明显减小、煤层渗透率增加［6］.Schutjens P M T M等应用地质力学模型研究盐丘构造周围生产诱导的应力场变化，采用地质力学有限元模拟器GEOMEC模拟盐丘的地质力学参数和生产对应力场的影响，分析井壁稳定和注入诱导的裂缝延伸［7］.

这些研究主要采用实验和数值模拟分析注入流体诱导的地应力场变化规律.笔者利用拉氏变换，以弹性力学理论为基础，结合注入流体诱导应力场的积分形式解，推导内、外边界在定压条件下拉氏变换解，并利用拉氏数值反演进行数值求解.

1 物理模型

当对油气井进行压裂改造或向注水井注水时，流体渗透到地层并引起孔隙压力升高，导致井筒周围应力场重新分布，使井周应力场发生变化，即为注入流体诱导的应力场［8－13］.注入流体诱导的应力场的物理模型见图1.假设条件：

（1）地层为无限大，井眼半径为rw，外边界半径为re，地层为均质油藏，地层渗透率K为各向同性；

（2）内、外边界定压，在井壁处压力为pw，在外边界处压力为pe；

（3）注入流体为微可压缩，其黏度μ和综合压缩系数Ct保持不变，不随压力变化；

（4）水平原始应力为各向异性，最大水平主应力为σH，最小水平主应力为σh；

（5）在注入过程中不考虑温度变化对地应力的影响；

（6）由于油藏厚度比泄油半径小得多，因此可以近似成平面应变（即二维情况）［13］；

（7）不考虑流固耦合，认为地层渗透率K、孔隙度不随压力或应力变化；

（8）极坐标系下径向应力为σr，周向应力或切向应力为σθ.

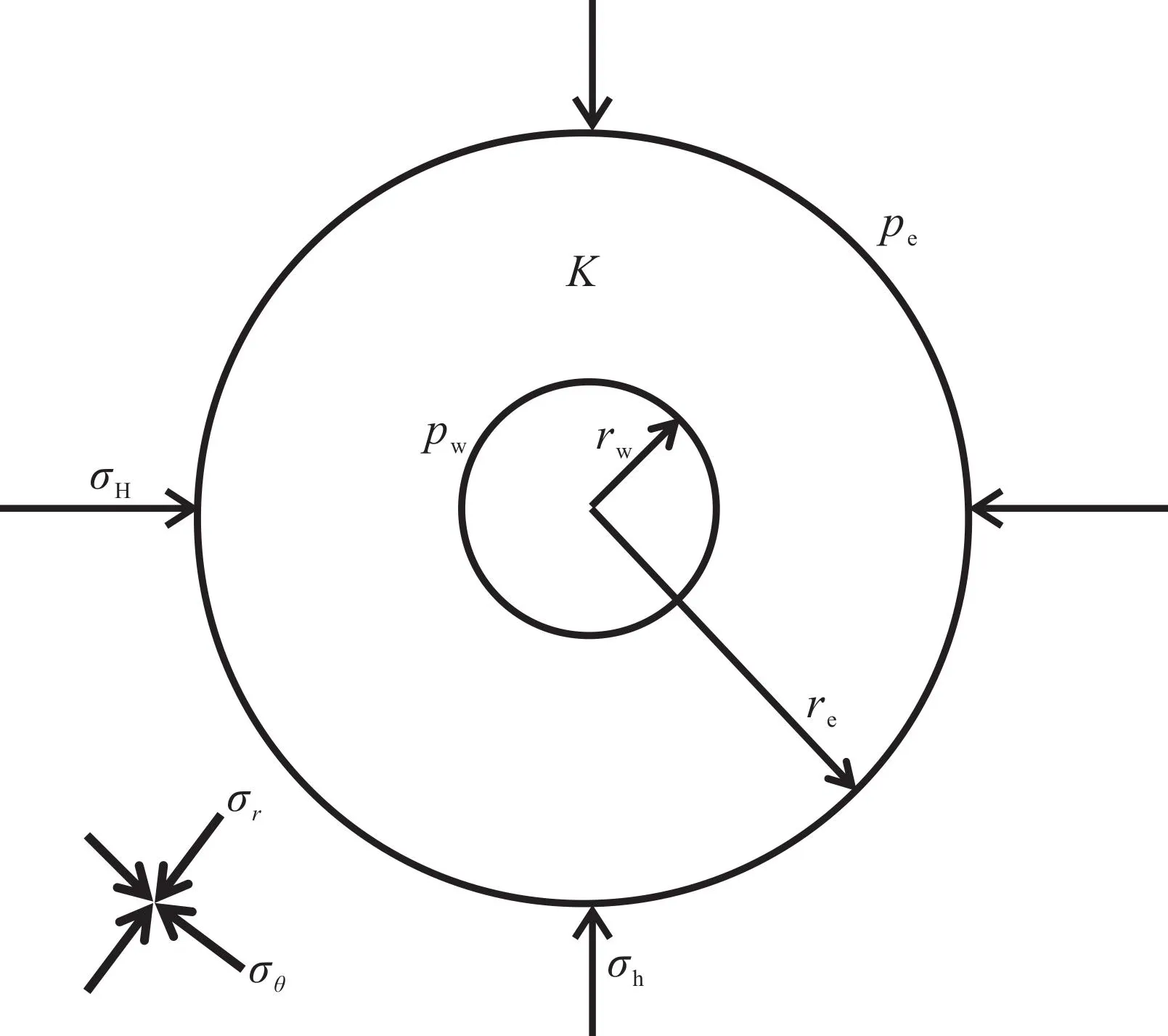
图1 注入流体诱导应力场的物理模型Fig.1 Physical model of the stress field induced by injection fluid

2 数学模型

2.1 计算公式

扩散方程［8］为

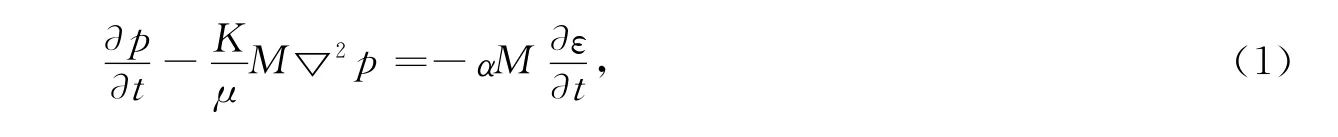
压力—应变关系式为

应力—应变关系式为

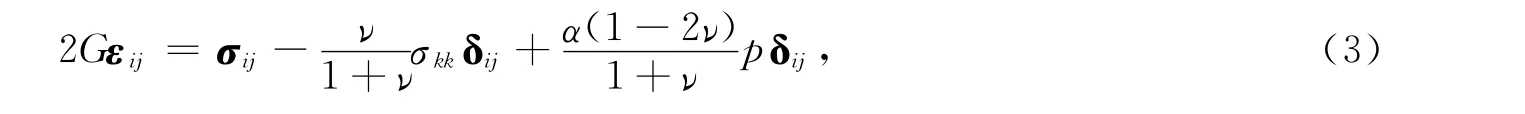
应变—位移关系式为

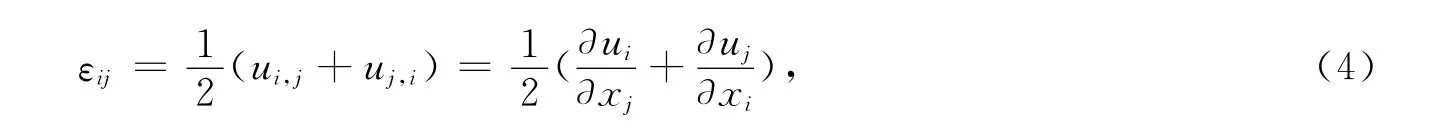
应力平衡方程为

连续性方程为

达西定律为

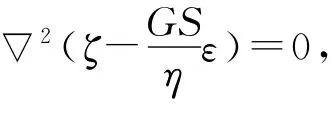
2.2 公式推导

因此通解为

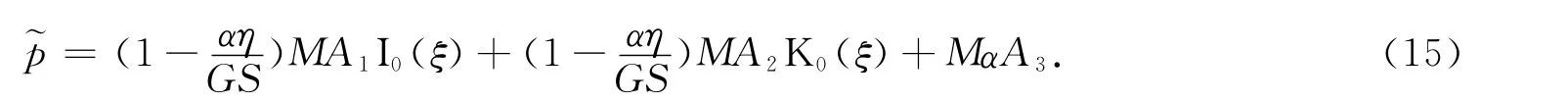
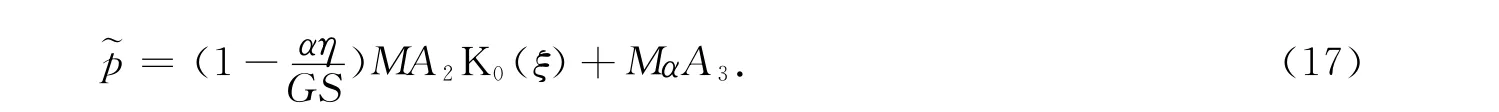
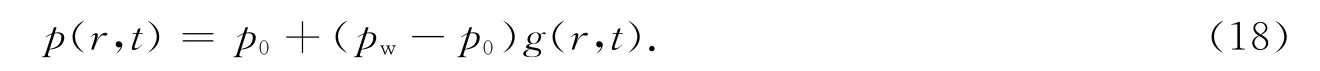
令pf（r，t）＝p（r，t）－p0，由文献［13－15］知注入流体诱导应力场积分形式解为

注入流体诱导径向应力

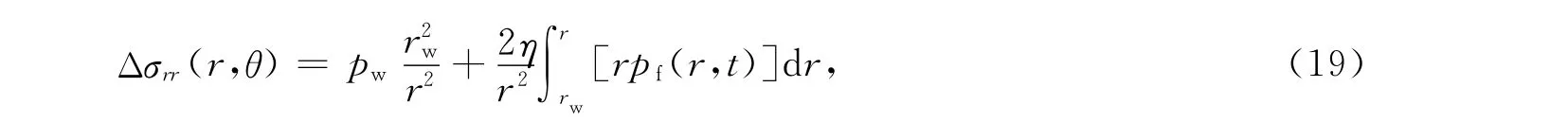
注入流体诱导切向应力

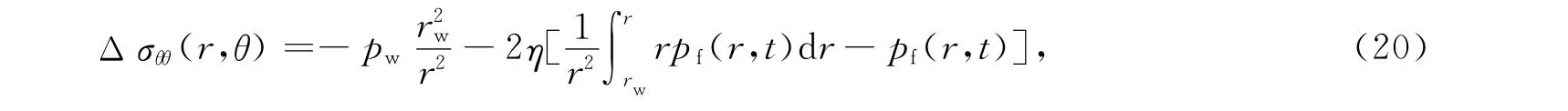
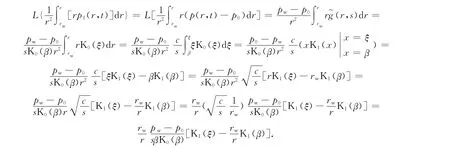
其中L－1（r，s））为g（r，t）的拉氏反演变换；K0（ξ）、K1（ξ）为零阶虚宗量第二类贝塞尔函数；I0（ξ）为零阶虚宗量第一类贝塞尔函数；A1、A2为s的函数.

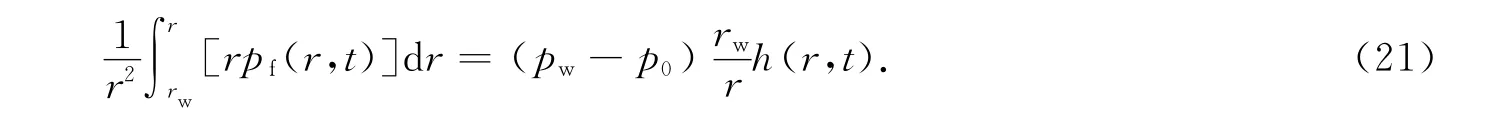
将式（22）分别代入式（19）和式（20）得到：

注入流体诱导径向应力

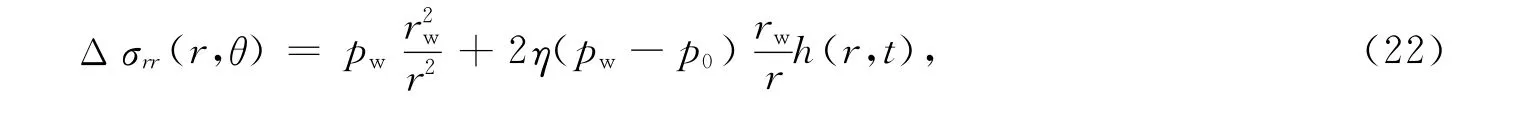
注入流体诱导切向应力

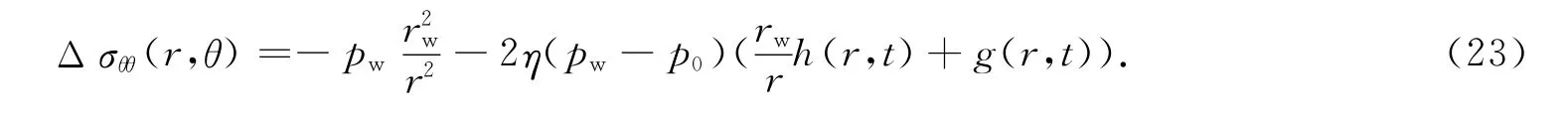
钻井后径向和切向地应力场分别为

2.3 求解方法

式（18）、式（22）和式（23）为拉氏变换解，应用Stephfest拉氏数值反演变换求其数值解［16］.

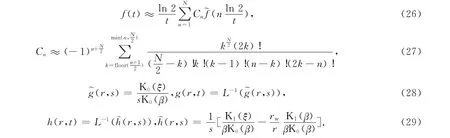
2.4 模型验证

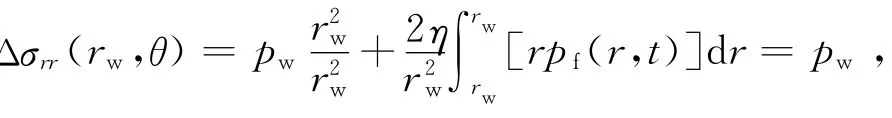
由式（23）得，Δσθθ（rw，θ）＝－pw－2η（pw－p0）；再由式（20）得，Δσθθ（rw，θ）＝－pw－2η（pw－p0），两者结果一致，并且与文献［17］式（12）与式（13）中代入r＝rw后结果一致，验证数学模型的可靠性.

3 切向应力场数值模拟

根据岩石张性破裂准则，人工裂缝的起裂主要与切向应力场相关，因此主要讨论注入流体后切向应力场的分布规律.地层和流体的基本参数见表1，利用式（25）模拟计算钻井后井筒周围原始切向应力（见图2）；根据式（23）、式（26－29）计算注入流体2.0h的诱导切向应力场分布，将它与钻井后井周原始切向应力场迭加，得到注入流体2.0h的新切向应力场（见图3）.由图2和图3可以看出，由于孔隙压力变化，使得切向应力场在最小水平主应力方向上变化较大，距离井壁越近，注入流体诱导的切向应力场值越大；随着距离井壁增加，其值变小.因此，注入流体后，孔隙压力的变化导致井筒周围切向应力场重新定向分布.

表1 地层和流体的基本参数Table 1 Basic parameters of formation and fluid

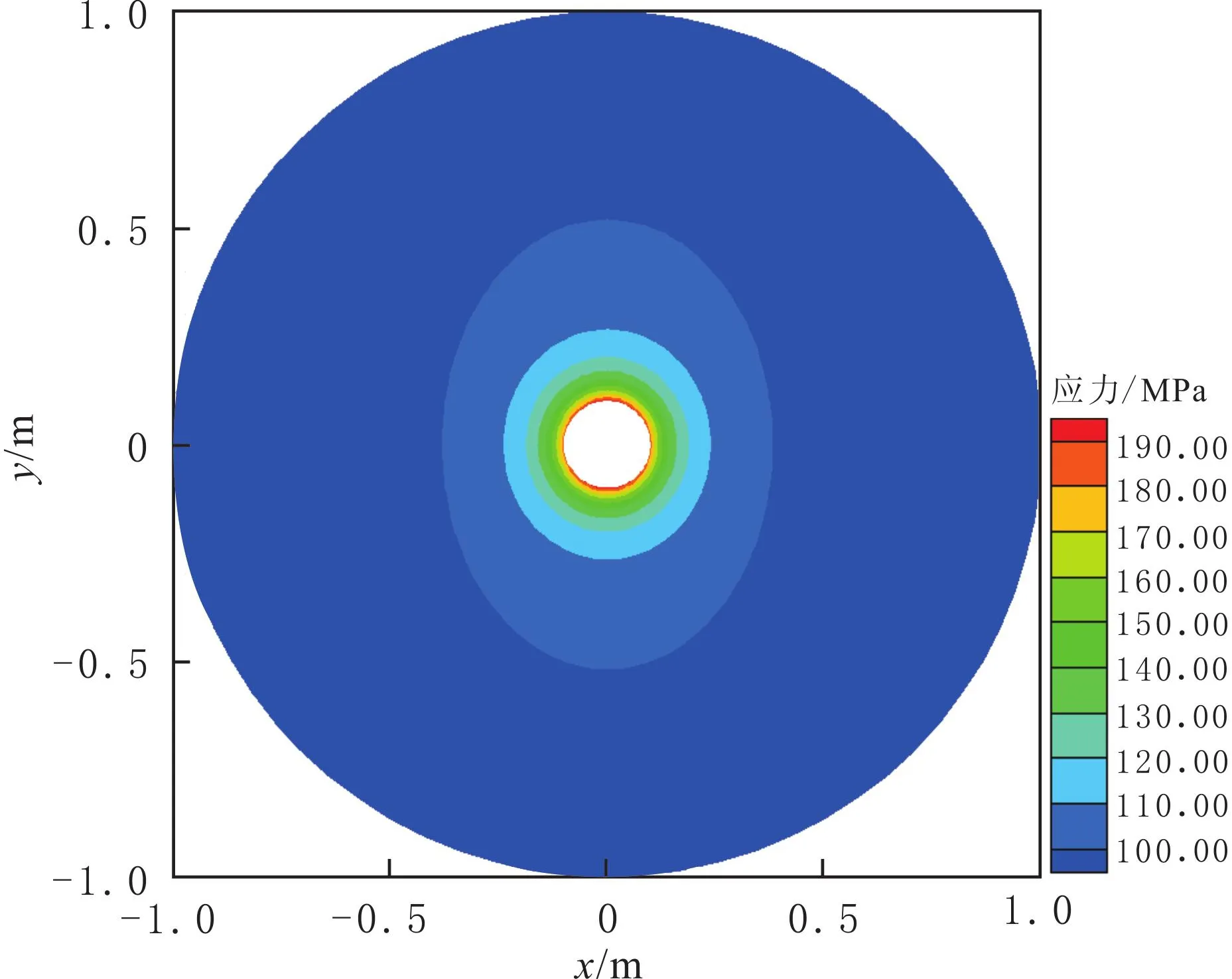
图2 钻井后原始切向应力场平面Fig.2 The original 2Dmap of tangential stress field distributon after drilling a borehole

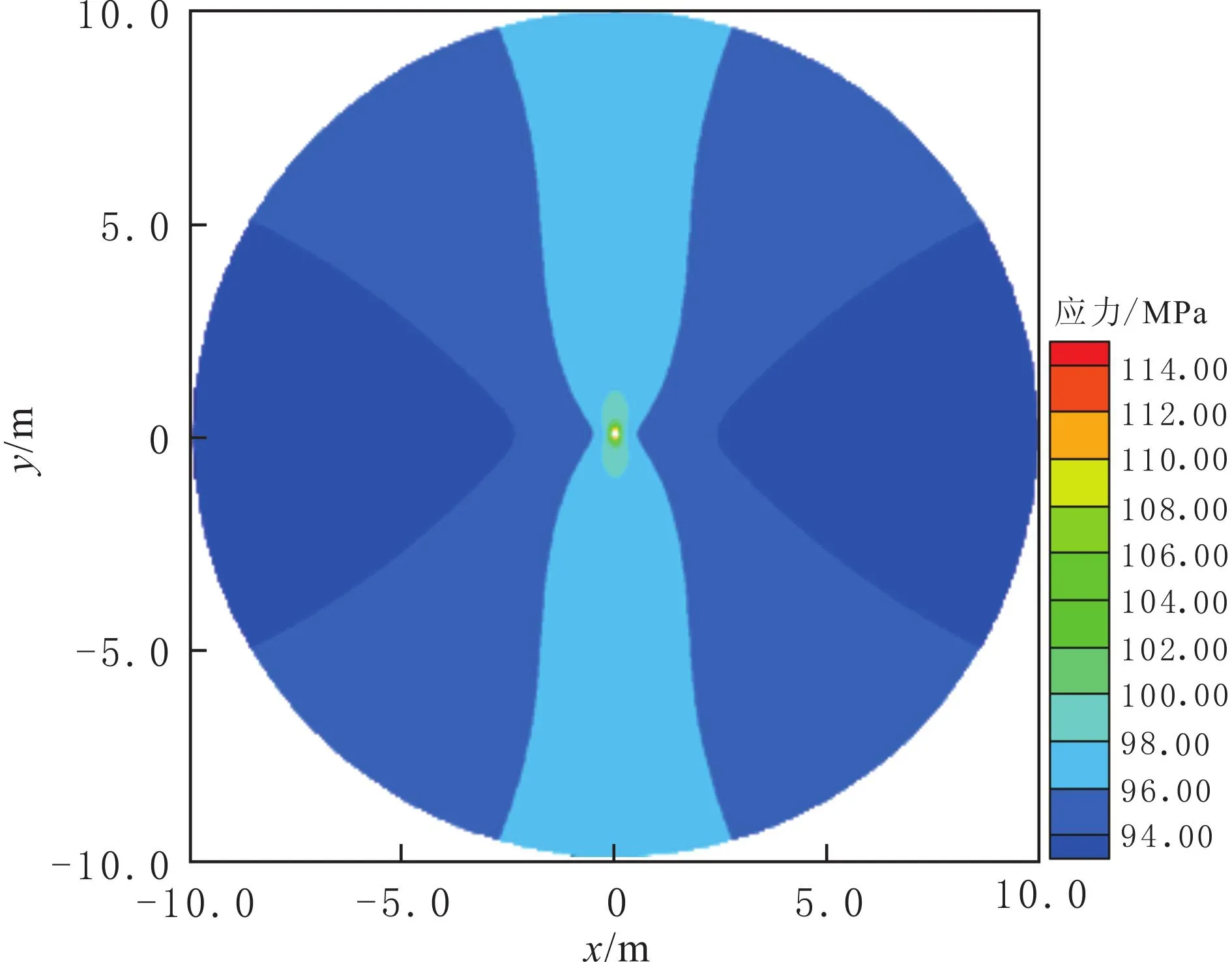
图3 注入流体2.0h的切向应力场平面Fig.3 The 2Dmap of tangential stress field distributon after injection fluid for 2.0hours

由于90°方向（对应最小水平主应力方向）上切向应力场变化明显，只需要讨论注入时间、流体黏度和地层渗透率对90°方向上切向应力场的影响规律.

3.1 注入时间

注入时间分别为0.5、2.0、4.0h的90°方向的切向应力场变化曲线见图4.由图4可以看出，随着注入时间增加，切向应力值增大，说明延长注入时间，增大注入体积，有利于增大90°方向的切向应力场值.这是由于随着注入时间增加，井底压力逐渐增加，井眼周围的孔隙压力也逐渐增加，从而导致切向应力值增大；并且90°方向上的切向应力场变化值大于0°方向上的，因此达到某一注入时间或注入量后，90°方向上的切向应力场值可能等于0°方向上的，使得原应力场重新定向［17－18］.这说明增大注入时间或注入体积使应力场重新定向反转、使压裂裂缝发生转向成为可能.

3.2 流体黏度

流体黏度分别为10.0、100.0、500.0mPa·s时90°方向上切向应力场变化曲线见图5.由图5可以看出，随着液体黏度提高，切向应力值变小.这是由于流体黏度越低，流动阻力越小，越容易进入更多的岩石孔隙，更容易改变孔隙压力分布，从而导致切向应力值增大，即将清水或低黏度流体（如滑溜水等）注入地层后，由于90°方向上的切向应力场变化值大于0°方向上的，使得原应力场重新定向.这说明注入低黏度流体使应力场重新定向反转、使压裂裂缝发生转向成为可能［17－18］，在非常规油气藏体积压裂中使用低黏度流体造缝可以增大裂缝复杂程度.

3.3 地层渗透率

地层渗透率分别为1.0×10－3、10.0×10－3、100.0×10－3μm2时90°方向上切向应力场变化曲线见图6.由图6可以看出，随着地层渗透率增加，切向应力场值变大.这是由于地层渗透率越高，孔隙压力传播越快，更容易改变孔隙压力分布，从而导致切向应力值增大.这说明对于高渗透油气藏，由于90°方向上的切向应力场变化值大于0°方向上的，注入一定体积流体或者生产一段时间后，原应力场较容易重新定向，使得重复压裂时机较短，应更早进行重复压裂施工［17－18］.

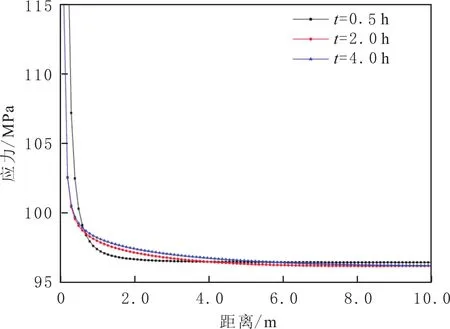
图4 注入时间对90°方向切向应力场影响曲线Fig.4 The curves between injection time and tangential stress field in the 90°direction

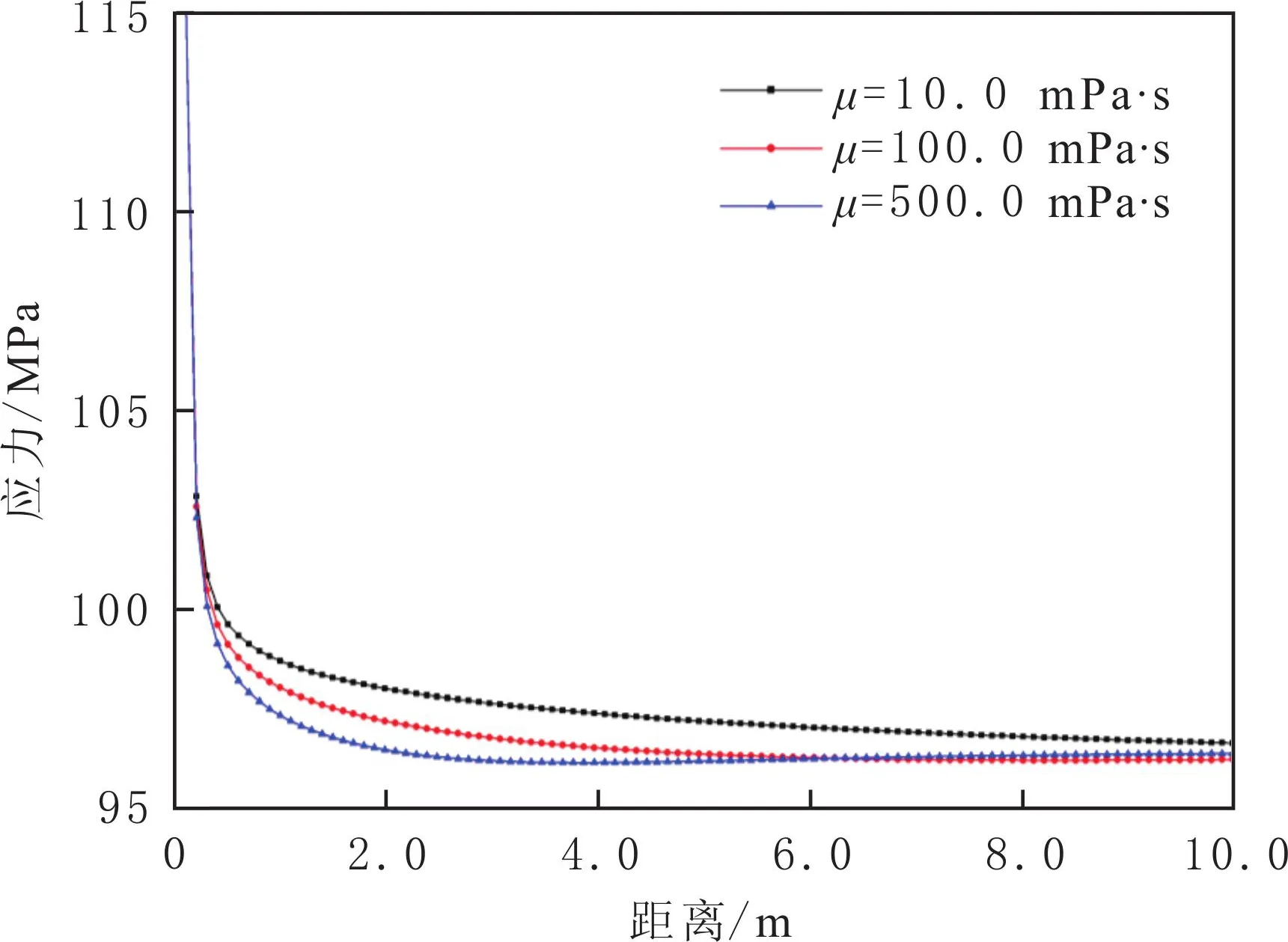
图5 流体黏度对90°方向切向应力场影响曲线Fig.5 The curves between fluid viscosity and tangential stress field in the 90°direction

3.4 现场应用效果

A井为我国某盆地某油田的油井，其油层段的水平主应力差值为3.00MPa，最大主应力方向为NE40°±，其储层段最大主应力方向为NW300°～330°，两者之间的夹角为85°±，储集体在显示段最大主应力方向上距离井眼55m（见图7）.2010年9月，进行可降解纤维暂堵转向酸压施工，第一级前置液无沟通显示，纤维暂堵转向剂到达位置后，在低挤入地层过程中，泵压上升约20.00MPa；在第二级压裂液注入过程中，排量未达到第一级排量，但泵压高于第一级的，虽无沟通显示，但注酸后泵压大幅下降，反应储层为裂缝型，已经实现转向造缝［24］.

基于注入流体诱导应力场、人工裂缝裂缝诱导应力场理论［17－24］，模拟A井的转向裂缝形态（见图8），产生转向半径为62.0m、与初压裂缝垂直的转向裂缝；当转向裂缝距初压裂缝的垂向距离超过62.0m后，应力场恢复到远场地应力状态，转向裂缝延伸方向与初压裂缝方向平行.

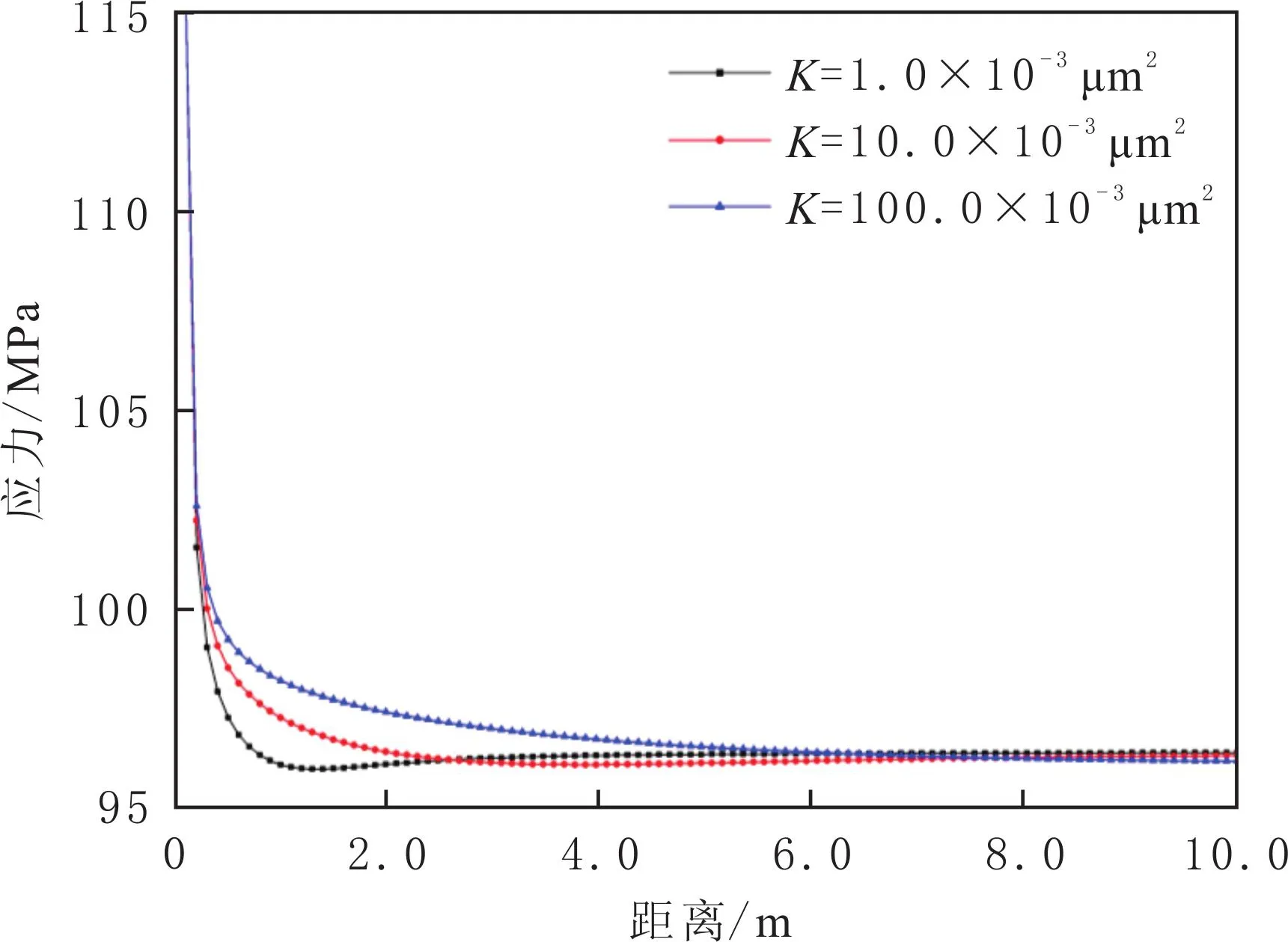
图6 地层渗透率对90°方向切向应力场影响曲线Fig.6 The curves between formation permeability and tangential stress field in the 90°direction

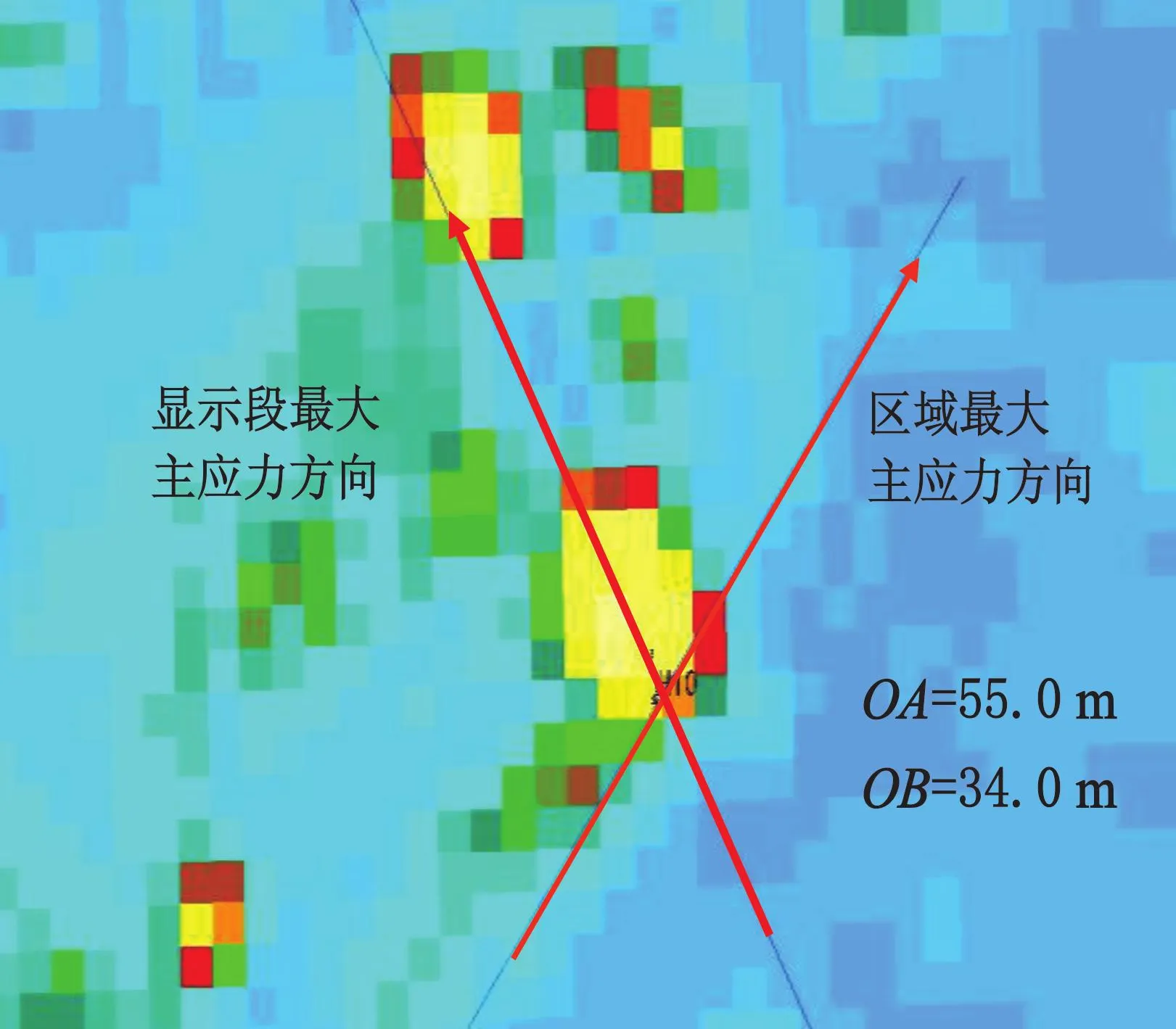
图7 A井储集体与最大水平主应力方位匹配关系Fig.7 The matching graph of reservoir and the maximum horizontal stress orientation in Well A

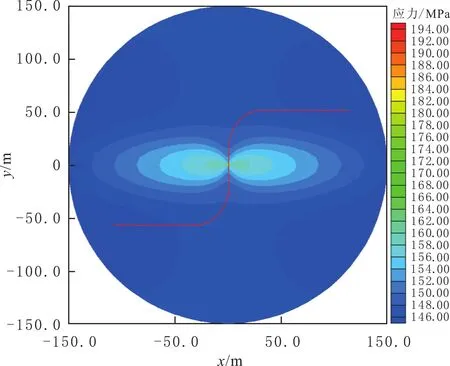
图8 A井转向裂缝形态平面Fig.8 The plane graph of fracture reorientation propagation path in Well A

模拟转向裂缝启裂角约为90°，转向半径为62.0m，A井储层段最大主应力方向与区域最大主应力方向夹角为85°，井眼距离串珠55.0m，两者结果基本接近，从而验证文中应力场数学模型的正确性［24］.

4 结论

（1）利用拉氏变换，以弹性力学的流固耦合控制方程和应力平衡方程为基础，结合注入流体诱导应力场的积分形式解，推导内、外边界在定压条件下的拉氏变换解，最后利用Stephfest拉氏数值反演对变换解进行数值求解.

（2）向井眼注入流体后，由于岩石孔隙压力发生变化，切向应力场重新定向.切向应力场在最小水平主应力方向上变化较大，距离井壁越近，注入流体诱导的切向应力场值较大，随着距离增加，其值变小；在一定条件下（如地应力差较小），切向应力场发生反转，使得压裂裂缝发生转向.

（3）切向应力场与注入时间、流体黏度和地层渗透率等因素有关：延长注液时间、增加注入流体体积、较低的液体黏度和较高地层渗透率有利于切向应力场增加，诱导切向应力场发生反转，使得压裂裂缝发生转向，增加泄油（气）面积与沟通机率.

（4）利用应力场拉氏变换解推导井壁周围的流体诱导应力场解，与文献的积分形式解得出的结果一致，从而验证数学模型的可靠性；将模型应用于油田现场，数值模拟结果与A井真实地质情况接近，从而验证数学模型的正确性.

（

）：

［1］ Elbel J L，Mack M G.Refracturing：Observations and theories［C］.SPE 25464，1993.

［2］ 范学平，徐向荣，张士诚.用流固藕合方法研究油藏压裂后应力应变和孔渗特性变化［J］.岩土力学，2001，22（1）：47－50.

Fan Xueping，Xu Xiangrong，Zhang Shicheng.Analysis on changes of stress strain porosity and permeability in multiphase reservoir with fluid－solid coupled and geomechanical mathematic simulation［J］.Rock and Soil Mechanics，2001，22（1）：47－50.

［3］ 张丁涌，赵金洲，赵磊，等.重复压裂造缝的应力场分析［J］.油气地质与采收率，2004，11（4）：58－59.

Zhang Dingyong，Zhao Jinzhou，Zhao Lei，et al.Analysis on stress field of refracturing fissure generation［J］.Petroleum Geology and Recovery Efficiency，2004，11（4）：58－59.

［4］ Weng X，Siebrits E.Effect of production－induced stress field on refracture propagation and pressure response［C］.SPE 106043，2007.

［5］ Sadegh Badakhshan Raz，Ahmad Ghassemi.Stress around a production well in gas hydtate－bearing formation［C］.AMRA 11－540，2011.

［6］ Liu S，Harpalani S.Gas prodution induced stress and permeability variations in coalbed methane reservoirs［C］.ARMA 12－642，2012.

［7］ Schutjens P M T M，Snippe J R，Mahani H，et al.Prodution－induced stress change in and above a reservoir pierced by two slat domes：A geomechanical model and its applications［C］.SPE 131590－PA－P，2012.

［8］ Emmanuel Detournay，Alexander H，Cheng D.Fundamentals of poroelasticity［M］.Fairhurst：Pergamon Press，1993：113－171.

［9］ Cui Lizheng，Younane Abousleiman.Time－dependent poromechanical responses of saturated cylinders［J］.Journal of Engineering Mechanics，2001，127（4）：391－398.

［10］ Jourine S，Valko P P，Kronenberg A K.Modelling poroelastic hollow cylinder experiments with realistic boundery conditions［J］.Int.J.Numer.Anal.Mech.Geomech，2004，28：1189－1205.

［11］ Chen Guizhong，Chenevert M E，Sharma M M，et al.A study of wellbore stability in shales including poroelastic，chemical，and thermal effects［J］.Journal of Petroleum Science and Engineering，2003，38：167－176.

［12］ Michael J E，Kenneth G N.Reservoir Stimulation［M］.3rd ed.New York，NY：Wiley，2000：80－85.

［13］ Zhai Zongyu.Fracturing and fracture reorientation in unconsolidated sands and sandstones［D］.PhD Dissertaiotion：The University of Texas at Austin，2006.

［14］ 孙庆友.大庆油田低渗透裂缝性油藏重复压裂造缝机理研究［D］.大庆：东北石油大学，2011.

Sun Qingyou.Research on the multiple fracturing mechanism of low permeability fractured reservoir in Daqing oilfield［D］.Daqing：Northeast Petroleum University，2011.

［15］ 刘洪，胡永全，赵金洲，等.重复压裂气井诱导应力场模拟研究［J］.岩石力学与工程学报，2004，23（3）：4022－4027.

Liu Hong，Hu Yongquan，Zhao Jinzhou，et al.Simulation study of induced stress field in refracturing gas well［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23（3）：4022－4027.

［16］ 严涛.压裂井试井理论与方法研究［D］.成都：西南石油学院，2004.

Yan Tao.Study on well test theory and method of fracturing wells［D］.Chengdu：Southwest Petroleum Institute，2004.

［17］ 宁淑霞.重复压裂井裂缝周围应力的重定向［J］.大庆石油学院学报，2007，31（4）：37－40.

Ning Shuxia.Stress re－orientation around fracturing of re－fractured wells［J］.Journal of Daqing Petroleum Institute，2007，31（4）：37－40.

［18］ 李玉伟，李修辅，刘佳，等.深井重复压裂裂缝起裂模型［J］.大庆石油学院学报，2009，33（5）：64－67.

Li Yuwei，Li Xiufu，Liu Jia，et al.Model of fracture initiation of the refracturing deep wells［J］.Journal of Daqing Petroleum Institute，2009，33（5）：64－67.

［19］ 田冷，肖聪，刘明进，等.考虑页岩气扩散的多级压裂水平井产能模型［J］.东北石油大学学报，2014，38（5）：93－102.

Tian Leng，Xiao Cong，Liu Mingjin，et al.Productivity model for multi－stage fractured horizontal well for shale gas reservoirs taking diffusion into consideration［J］.Journal of Northeast Petroleum University，2014，38（5）：93－102.

［20］ 孙学增，孙茂凤，张文，等.椭圆度对井眼拉伸和挤毁破坏的影响［J］.大庆石油学院学报，1998，22（3）：14－17.

Sun Xuezeng，Sun Maofeng，Zhang Wen，et al.Effects of ellipticity on the tensile and collapse failure of a borehole［J］.Journal of Daqing Petroleum Institute，1998，22（3）：14－17.

［21］ 蔡明金，贾永禄，陈得寿，等.三重介质油藏垂直裂缝井产量递减曲线［J］.大庆石油学院学报，2009，33（5）：60－63.

Cai Mingjin，Jia Yonglu，Chen Deshou，et al.Production decline curve for wells with vertical fractures in triple－porosity reservoir［J］.Journal of Daqing Petroleum Institute，2009，33（5）：60－63.

［22］ 郑宪宝，李文娟，刘振宇.人工压裂井数值模型［J］.大庆石油学院学报，2008，32（4）：31－48.

Zheng Xianbao，Li Wenjuan，Liu Zhenyu.Numerical modeling of artificial fractured wells［J］.Journal of Daqing Petroleum Institute，2008，32（4）：31－48.

［23］ Gong X，Wan R，Mohamadi M.Coupled fluid flow－thermoplastic deformation of oil sand and shale in SAGD process［C］.SPE 165501－MS，2013.

［24］ 汪道兵.直井纤维暂堵转向压裂裂缝启裂与延伸数学模型研究［D］.成都：成都理工大学，2013.

Wang Daobing.Study on the mathematical model about the fiber temporary plugging diverting fracturing crack initiation and propagation of the vertical wells［D］.Chengdu：Chengdu University of Technology，2013.

注入流体诱导应力场模拟计算

汪道兵1，2，葛洪魁1，周福建1，熊春明2，张景臣3，严星明4

DOI 10.3969／j.issn.2095－4107.2015.02.011

TE312

A

2095 4107（2015）02 0085 09

2014 11 10；编辑：任志平

国家重点基础研究发展计划项目（2015CB250903）；国家自然科学基金重大项目（51490652）；中国石油天然气股份有限公司科学研究与技术开发项目（2010E－2105）

汪道兵（1985－），男，博士研究生，主要从事非常规储层缝网形成与控制机理方面的研究.