基于遥感影像的地表三维可视化技术研究

蒋诗龙，白 林

(成都理工大学 数学地质四川省重点实验室，四川 成都 610059)

0 引 言

三维重建技术能精确地对物体进行模拟构建，可以给用户带来更真实的体验.其实际应用主要有3 个方面:一是在虚拟地理环境、城市规划、旅游规划、“数字地球"、地理信息系统等实际应用方面;二是三维地震资料的解释和矿产勘查方面的地质三维景观模拟;三是大气、海洋科学中的科学计算可视化［1］.三维重建技术为人与自然交互和探索提供了新的平台，通过各种数学模型、算法和理论在计算机上建立三维可视化模型，已经预示了其美好的应用前景.由于地质问题的复杂性和应用的特殊性，实际中难以提出通用的三维数据模型，往往根据研究领域具体描述对象的特点或功能要求进行特别考虑而设计出各具特色的三维数据模型.目前，三维地质建模方法主要划分为基于面的建模方法、基于体的建模方法、混合建模方法［2－3］.基于面的建模方法表示的模型众多［4－11］，如规则格网(Grid)、不规则三角网(Triangulated Irregular Network，TIN)、边界表示法(Boundary Representation，BRep)和参数函数等，侧重于三维实体的表面表示.

随着电子计算机技术和航天科技的日益发展，人们对认识大气、陆地、海洋等的需求不断提高，遥感技术不断发展，在空间测量、资源勘查、城市导航、军事侦察等领域得到了广泛的应用.遥感影像的三维重建技术是三维地形模拟中的一个重要研究热点.由于地表景观通常较为复杂，采用一般的纹理映射难以达到真实的三维效果，而遥感影像能真实表现地形地貌特征，因此被广泛应用于地表三维可视化中.通过几何校正、辐射校正、噪声消除等处理，将高分辨率的正射遥感影像作为纹理映射到三维数据模型表面，实现真实景观环境的数字化虚拟［12］，可以大大增加三维地表模型的真实感与临场感.

1 遥感影像的预处理

在遥感成像的过程中，由于各种因素使遥感影像失真，为了使遥感影像更好反映原始地物特征，在进行分析应用之前，都必须进行相应的影像预处理.作为研究对象的大巴山地区的遥感影像(见图1(a))在中心区域的色彩丰富、饱和度高、灰度较均匀，但是可以明显看出左边部分曝光度过高，灰度过于集中，层次较少，明度和饱和度较低，不适合直接用于三维叠加.因此需要对原始图像进行辐射增强的处理.

首先使用Photoshop 对左边亮度过高部分进行了灰度系数校正，校正系数为0.55，同时设置了曝光度为0.16，使显示亮度和其他区域相对统一.在处理过程中发现图像的灰度直方图主要集中在左侧，整幅图色调偏暗，因此对直方图进行了均衡化处理［13］，使影像的灰度概率密度均匀分布.基本原理如下:设非均匀概率密度函数为P(r)，变换函数为T(r)，均匀概率密度函数为P(s)，其中，s=T(r)，可知直方图均衡化的关键是求得T(r).

假定T(r)满足:1)在区间0≤r≤1 内是单调递增函数，且满足0≤T(r)≤1;2)反变换r=T－1(s)存在.那么由概率论知，P(s)=P(r)dr/ds，又因为直方图均衡化时P(s)=1，所以有ds=P(r)dr，两边积分得s=P(r)dr=T(r)，显而易见s 在定义域内是均匀分布的.

经过辐射增强后可以看出高亮度区被压缩，低亮度区被扩展，图像质量明显改善.图1(a)为原始图像，1(b)为辐射增强后的图像.

图1 辐射增强前后影像图

为了保证影像校正后的质量，分别对1∶ 50 000大巴山地区地形图和TIN 模型进行控制点选取.在选取过程中发现影像图范围过大，因此对影像图进行了适当裁切.在TIN 模型中选择了容易识别的点如河流的交叉点、山脊线的交叉点等.多项式校正控制点的最少数目是((t +1)×(t +2))/2 个，其中t是多项式阶数.为了提高精度，选择了二次多项式，控制点为图中均匀分布的6 个点.本研究遥感图像的几何校正使用ERDAS IMAGINE 9.0，其中的AutoSync 模块能通过动态监测不同分辨率精确判断纠正点的位置.

2 基于不规则三角网的DEM 生成

DEM 的数据来源大致有2 种，第一种是通过航摄法，二是通过地形图生产DEM 数据.由于地形图相对较为便宜，并且有较高的精度，也容易获得.因此本研究利用数字化软件的自动跟踪采集功能处理大巴山该区域的地形图.目前很多GIS 厂商推出的商业软件都支持扫描的功能，比如ArcMap、PCI、ScanIn 等都可以采集和编辑等高线;ScanIn 软件的特点体现于人机交互式跟踪，进行扫描时能够自动跟踪线状要素，当遇到毛刺、文字、污点或断点时就会自动停止跟踪.若人工指出继续跟踪的方向，则会继续工作.

广义上等高线模型、不规则三角网(Triangulated Irregular Network，TIN)和规则格网(Grid)都可以称为数字高程模型，其中TIN 是将有限、无重复的离散数据点集进行三角剖分，使得离散点形成连续的非重叠的三角网格，进而构成一个面.每个三角网点都包含了该点的平面位置信息和高程信息.Delaunay三角网是在有限点集中具有最优性的三角网，相对于规则格网具有数据冗余少的特点.目前Delaunay三角形常用的生成算法有3 种，分别为逐点插入算法、三角网生长算法和分治算法.本研究主要分析和对比了前2 种算法.

为了比较这2 种算法，分别使用2 种算法在内存为3.43 GB、显存为2 547 MB 的微机上对等高线离散化的200 个离散点进行不规则三角网生成，如图2 所示，并计算了其消耗的时间，对比结果见表1.

图2 离散点生成TIN

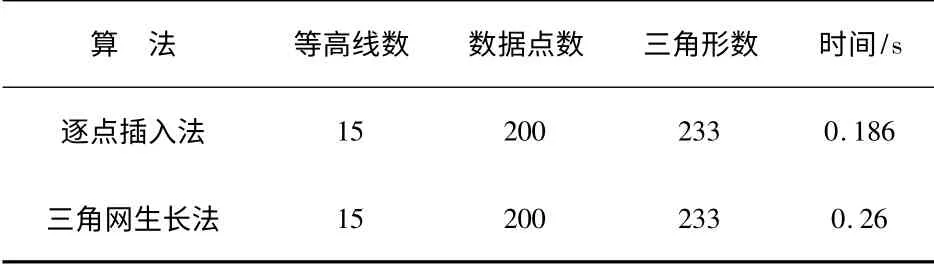
表1 离散点三角网生成的时间消耗

实验发现，逐点插入法的效率高于三角网生长法，这是因为三角网生长法在每个三角形的形成时都会判断一次待处理点.在改进的三角网生长算法中，虽然可以通过分块或排序提高效率，但是很难彻底解决问题，当数据点较多时，时间复杂度比逐点插入法更高，同时逐点插入法由于建立了线性链表保证了相邻数据点的逐次插入，提高了构建三角形的效率.考虑到本研究的离散点较多，因此采用逐点插入法对大巴山地区1∶ 50 000 等高线进行TIN 的转换.根据ArcMap 中的计算可知其中等高线4436 条，离散点1 154 717个，生成三角面2 309 230个.利用ArcToolbox 中的插值工具可以很容易计算出TIN.

虽然TIN 的精度很高，但是TIN 的数据存储方式比较复杂，不仅要存储每个点的高程信息，并且还需要存储点的平面坐标、节点间的拓扑结构、三角形之间的关系［14］，所以导入TIN 的速度相对较慢.为了使DEM 模型在和遥感影像叠加的过程中能更加流畅，本研究将TIN 通过自然邻域插值法转化为栅格图形，再利用栅格图形中的高程值使遥感影像具有三维效果.这样能大大提高叠加的速度.自然邻域插值法(Natural Neighbors)是对最临近查询点的样本子集的区域大小加权平均.正因为这个方法只使用查询点周围的样本子集，所以其插值范围比较固定.本研究中定义的采样距离是当栅格最长边为250 个单位时，像元大小为1.888268，像元越小图像越细腻，但是占用内存就会越大.转换后的栅格图像如图3 所示.

图3 DEM 栅格图

3 一阶多项式地理配准与误差分析

设x、y 为DEM 坐标，X、Y 为对应遥感影像坐标，m1、m2为横向与纵向比例尺，α 为两坐标系夹角，则可以得到变换的旋转矩阵为，

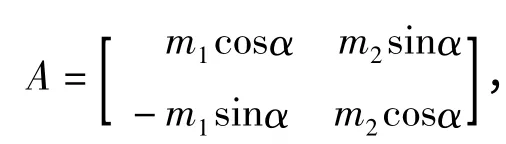
得出一阶多项式变换公式，

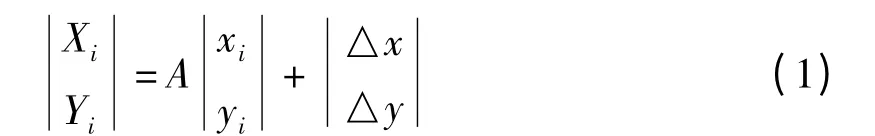
其中，△x、△y 为两坐标原点的平移量.设△x =a0，m1cosα= a1，m2sinα = a2，△y = b0，－ m1sinα = b1，m2cosα=b2.

由式(1)可知当有3 对控制点时，就能计算出a0、a1、a2、b0、b1、b2，也就实现了一阶多项式变换.通过3 对控制点的DEM 坐标与对应的遥感影像图坐标(见表2)计算出的RPC 参数如下:

a0=19973.74888，a1=0.97612，a2=－0.00013698，

b0=4721277.43093，b1=－1.454853，b2=－0.0029587.

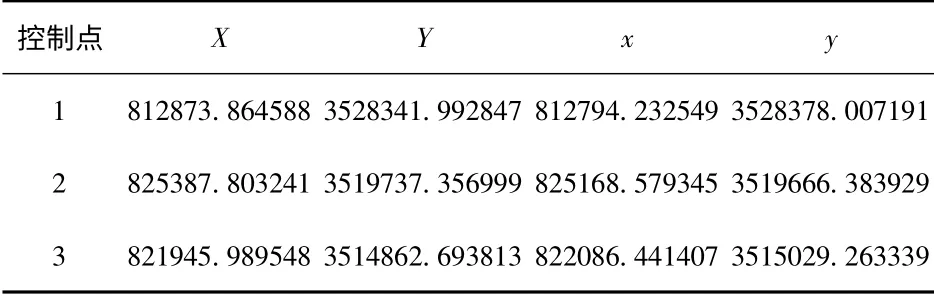
表2 3 对控制点的坐标

根据上述3 个控制点的坐标，计算出残差与RMS 数据见表3.可以看出，总误差满足精度要求.

4 遥感影像三维可视化

ArcScene 是一个具有3D 要素的显示、编辑、分析功能的三维模块，广泛用于GIS 影像处理中，其最主要用来对要素进行立体显示与分析，包括二维要素和三维要素.常见的有点要素、线状要素和多边形要素，遥感影像属于二维的多边形要素.在ArcScene中想要以三维形式显示要素，必须将要素赋予高程值，缺少高程值的要素可以通过叠加的方式在三维场景中显示.本研究采用该方式，将遥感影像所在区域的数字高程模型的高程值作为影像的高程值，就可以显示出立体效果.图4 为大巴山地区最终生成的三维效果图.

图4 大巴山地区三维效果图(局部)

5 结 论

本研究对基于遥感影像的地表三维可视化技术进行了研究与实现，主要实现了高程数据的获取和数字高程模型的构建，对比了2 种三角网生成算法，利用自然邻域法对TIN 构建了DEM 栅格图，提高了叠加过程的效率.在此基础上，研究出快速构建地表三维模型的技术流程，其可为地质勘查、城市选址、灾害评估等领域快速生成地表的三维基础资料.

［1］王明孝，张志华.地理空间数据可视化［M］.北京:科学出版社，2012.

［2］郑贵洲，申永利.地质特征三维分析及三维地质模拟现状研究［J］.地球科学进展，2004，19(2):218－223.

［3］Boissonnat J D.Geometries structures for three-dimensional shape representation［J］.ACM Trans Graph，1984，3(4):266－286.

［4］潘懋，方裕，屈红刚.三维地质建模若干基本问题探讨［J］.地理与地理信息科学，2007，23(3):1－5.

［5］Moore Ross R，Johnson S E.Three-dimensional reconstruction and modeling of complexly olded surfaces using mathematica［J］.Comp ＆ Geosci，2001，27(4):401－418.

［6］王宝军，施斌，宋震.基于GIS 与虚拟现实的三维地质建模方法［J］.岩石力学和工程学报，2008，27(S2):3563－3568.

［7］张晓坤，章浩.三维地质建模在矿产资源开发中的应用［J］.金属矿山，2010，45(3):106－110.

［8］张宝一，尚建嘎，吴鸿敏，等.三维地质建模及可视化技术在固体矿产储量估算中的应用［J］.地质与勘探，2007，43(2):76－81.

［9］刘文玉，吴湘滨，张宝一，等.红透山矿区三维地质建模与可视化研究［J］.科技导报，2011，29(11):48－51.

［10］陈学工，李源，曹建，等.Delaunay 三角网剖分的约束边嵌入改进算法［J］.计算机工程与应用，2009，45(24):235－237.

［11］僧德文，李仲学.地矿工程三维可视化仿真系统设计及实现［J］.辽宁工程技术大学学报(自然科学版)，2008，27(1):9－12.

［12］刘颂.基于遥感影像的三维地形景观模拟技术初探［J］.系统仿真技术，2005，1(2)，116－119.

［13］邓书斌.ENVI 遥感图像处理方法［M］.北京:科学出版社，2012.

［14］侯波.卫星遥感影像三维可视化处理［J］.中国体视学与图像分析，2001，6(1):29－32.