俄罗斯经济发展形势的分析与预测

徐坡岭　刘来会

摘 要：本文采用俄罗斯2002—2013年的季度数据作为样本，主要分析了季节性差分自回归模型——SARIMA模型在俄罗斯季度GDP预测中的应用，通过相应的分析最终得到了SARIMA（1，1，0）（1，1，0）4为俄罗斯季度GDP的最优预测模型。通过该模型对俄罗斯短期和长期经济发展形势进行了预测，得出俄罗斯未来四年的GDP年增长率在2.3%左右，长期的经济增长率在2.1%左右，经济形势依然不容乐观。

关键词：俄罗斯经济； SARIMA模型； 季度GDP

中图分类号：F753 文献标识码：A 文章编号：1000-176X（2015）02-0117-06

一、引 言

2008年以来俄罗斯经济陷入持续低迷状态，观察俄罗斯近几年GDP增长率的变化，可以看出，在2009年GDP增长率存在一个明显的断点，在2009年之前GDP年均增长率为7.1%，2009—2013年年均增长率仅为1.1%，显著低于之前的水平。尤其2013年俄罗斯GDP的增长率只有1.3%，这是经济增长的急剧减速，同时1.3%的经济增长水平低于当年世界3%的平均增长率1.7个百分点，在过去12年中，除2009年外这是从来没有过的。在经历了2009年短暂复苏之后似乎又陷入严重低迷状态。俄罗斯经济增长的这种低迷状态引起了各国学者的广泛关注，对俄罗斯经济未来发展形势的分析，是当今研究的一个热点问题，许多学者也提出了自己的看法。 Замараев[1]等认为，俄罗斯在2008—2009年经济恢复性增长已经完成，但原料经济以及国外资本流入减少等因素的限制，影响了国民经济的整体表现，俄罗斯经济增长将会再现不同于“塌陷的”1990年和“肥胖的”2000年的第三条经济增长轨迹。 Мау[2]指出，俄罗斯未来会形成新的经济增长模式，而新的经济增长模式正是经济危机的产物。 Алексашенко和 Миронов[3]认为，2008—2009年的经济危机是第一次严重影响俄罗斯经济的世界性危机，但是这可能不是最后一次，俄罗斯已成为世界经济的一份子，在这过程中任何不稳定因素都可能严重影响俄罗斯经济，如果俄罗斯不进行结构性改革，下一次经济危机俄罗斯将受到双倍打击。国内外学者对于俄罗斯经济的研究主要集中于俄罗斯经济低迷的原因和未来经济结构调整。邢国繁和张曙霄[4]认为，俄罗斯经济2009年以来发生逆转的根本原因在于俄罗斯单一的资源型经济，造成对外部环境的过度依赖，发展创新型经济是其未来经济发展的必然选择。苗华寿[5]在对俄罗斯经济低迷原因进行分析的基础上指出，俄罗斯经济目前还难以摆脱对自然资源和外部市场的依赖，作为一个资源型超级大国、一个有着较高教育和科技水平的国家，俄罗斯当局振兴经济的能力还是不能低估的。通过以上的研究笔者发现，大多数学者的研究集中在对俄罗斯发展形势的理论分析，很少涉及到对俄罗斯经济的定量分析，因此笔者认为有必要利用相应的数据，对俄罗斯未来经济的发展做一个系统的分析与预测。

二、 数据来源及方法选择

1.数据来源及说明

为提高模型预测的准确性，本文采用2002—2013年俄罗斯季度GDP，数据来源于俄罗斯联邦统计局，以2008年价格作为基期，同时为了对所建立预测模型的准确性进行分析，本文选取2002—2012年的季度数据用于模型的构建，2013年的季度数据用于检验模型预测的精确度，

2.模型比较与选择

时间序列分析方法是把统计资料，按时间发生的先后进行排序得出一连串数据，利用该数据序列外推到预测对象未来的发展趋势。常用的有指数平滑法、差分自回归移动平均模型、自回归移动平均模型、移动平均模型和季节性差分自回归滑动平均模型等。

指数平滑法又称指数加权平均法，在1959年由美国学者布朗首先提出，它是通过计算指数平滑值，配合一定的时间序列预测模型对现象的未来进行预测。其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均，也就是根据已有变量预测未来变量的发展趋势。它主要包括：一次指数平滑法、二次指数平滑法和三次指数平滑法。指数平滑法在实际中得到了广泛的应用，但是这种方法并不适合具有周期性和季节性数据的预测。

ARMA模型也就是自回归移动平均模型，它是自回归过程（AR）与移动平均过程的组合得到ARMA（p，q），它的模型可以表示为：

其中，εt为白噪声的序列，p和q分别为自回归和移动平均阶数，βp和θq为待估参数。运用ARMA模型要求序列必须平稳，因此ARMA模型主要对平稳时间序列进行分析。

ARIMA模型是在ARMA模型基础上进行的改进，如果序列不是平稳时间序列，需要进行d阶差分才可以变为平稳时间序列，这就需要建立ARIMA（p，d，q）模型，即不平稳的时间序列通过d阶差分变为平稳时间序列。这种模型不考虑以经济理论为依据的解释变量的作用，而是依据变量本身的变化规律，利用外推机制描述时间序列的变化[6]。在实际应用中很多时间序列呈现出季节性周期变化，对于这类数据，可以通过季节ARIMA模型（Seasonal ARIMA，简记为SARIMA）进行拟合，模型为：

其中，下标p、q分别为非季节自回归、移动平均算子的最大滞后阶数，P、Q分别表示季节自回归、移动平均算子的最大滞后阶数；d、D分别为非季节和季节性差分次数[7]。

SARIMA模型可以消除季节性和周期性影响[8]，由于本文的数据是来自俄罗斯的季度GDP数据，在以下的分析中可以看到，该数据呈现明显的周期为4的季节性，因此，本文的分析主要建立在SARIMA模型基础之上。

三、经验分析

1.平稳性与季节性检验与处理

时间序列模型的预测，要求数据必须是平稳的，因此需要对数据进行平稳性检验，在此之前，为了增强数据的稳定性，需要对数据进行对数化处理。图1是对数化季度GDP的时间趋势图。从图1可以看出，季度GDP变动具有明显的时间趋势和周期性，可以直观地根据经验判断序列是非平稳的。

为了确定lnGDP的单整阶数，需要进一步检验lnGDP的一阶差分dlnGDP的平稳性，同时由图1还可以看出时间序列具有明显的季节周期性，由于笔者使用的是周期为4的季度数据，因此，为进一步消除季节性，笔者尝试同时使用s=4的季节差分处理，图2为经过一阶差分和四阶季节差分的时间序列趋势图。由图2可以看出，经过一阶差分和四阶季节性差分后的lnGDP的时间序列在0附近波动，因此可以初步判断时间序列是平稳的，再次使用ADF检验进一步实际验证时间序列的平稳性，检验结果如表3所示。由表3可以看出，ADF统计量Z（t）值，可以在1%的显著性水平上拒绝存在单位根的原假设（Z（t）<-3.7），可以认为经过季节性差分的时间序列是平稳的时间序列。

2.模型的识别

由上述分析可以得出，原序列是非平稳序列，并且存在4期的滞后。经过一阶差分和一阶季节差分后序列通过了平稳性检验，符合建模的平稳性要求，同时，因为其具有明显的季节性，适合建立季节调整的SARIMA模型。

（1）模型的建立

SARIMA的建立首先要进行选择才能建立模型，所以要建立SARIMA（p，d，q）（P，D，Q）s模型就要涉及到p，q以及P，Q的确定问题。通过前文分析已经知道，序列经过一阶差分和四步季节差分可以通过平稳性检验，因此这里的d=D=1，s=4，所以剩下的问题就是确定p，q以及P，Q的值。图3和图4分别是一阶差分和四阶季节差分后的自相关和偏自相关图。

根据自相关函数和偏自相关函数的特征，可以综合考虑预选模型，对SARIMA（1，1，1）（0，1，1）4 ，SARIMA（2，1，1）（0，1，1）4 ，SARIMA（0，1，1）（0，1，1）4 ，SARIMA（1，1，0） （0，1，1）4，SARIMA（1，1，0）（1，1，0）4 分别进行比较。通过分析只有SARIMA（0，1，1）（0，1，1）4、SARIMA（1，1，0）（0，1，1）4和SARIMA（1，1，0）（1，1，0）4的系数在5%的显著性水平下全部通过了检验。进一步通过AIC、BIC准则来选择判定模型，模型根据AIC、BIC最小准则进行选择。

由表4可以得出，SARIMA（1，1，0）（1，1，0）4的AIC和BIC最小，分别为-192.5、-187.5，根据AIC、BIC最小准则，而且根据这三个模型预测值与实际值的比较，该模型的拟合效果是最好的，可以选择该模型作为最优预测模型。最终得到的SARIMA模型如下：

（2）模型的诊断

SARIMA模型建立之后还需要进行模型的显著性检验，即对模型的残差进行白噪声检验，若残差为白噪声，则意味着所建立的模型包含了原始序列的所有趋势从而模型应用预测是合适的，反之若残差不是白噪声序列说明模型还需要进行改进[9-10]。

通过残差检验结果可以得出，Q统计量为12.8，概率>χ2（17）为0.7，因此，不能拒绝残差为白噪声的原假设，说明模型的拟合效果是不错的，可以使用该模型作为预测模型。

四、模型的预测

1.模型的预测精度分析

通过2002—2012年俄罗斯季度数据的分析，笔者得出俄罗斯季度GDP的预测模型SARIMA（1，1，0）（1，1，0）4，笔者利用该模型对2013年1—4季度的GDP进行预测，将预测值与官方公布数据进行比较，数据结果如表5所示。

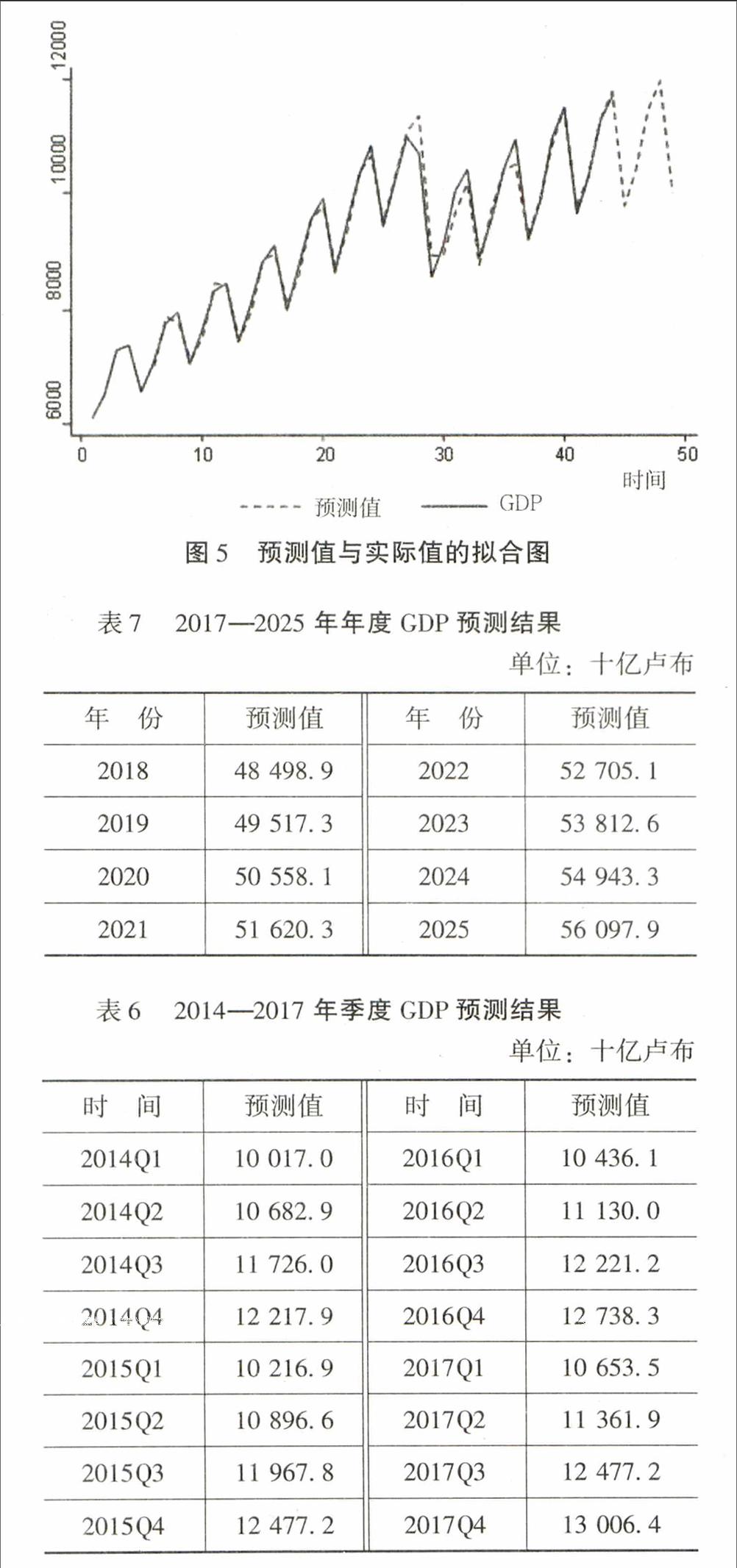
预测结果表明，预测值和实际值很接近，预测的相对误差很小，而且通过图5预测值和实际值的拟合图，可以看出，该模型预测值基本较好的拟合了实际GDP的发展趋势，由于模型仅仅考虑时间序列自身变动的规律，未考虑其他外在因素的变化，再加上建立模型本身的误差，偏差不可避免，但总体来说所建立的预测模型可行。

2.预测结果的分析

在以上分析结果的基础之上，本文使用该模型对俄罗斯未来十年的经济形势进行了预测，当然鉴于模型的预测结果随着时间的推移准确度会下降，因此，本模型长期的分析结果还是需要进一步的完善。表6列出了2014—2017年俄罗斯的季度GDP的预测结果。

根据表6预测结果，2014—2017年的季度GDP呈现缓慢增长趋势，根据预测，2014—2017年第一季度的GDP同比平均增长率为2.3%，第二季度GDP平均增长率为2.3%，第三季度平均增长率为2.3%，第4季度平均增长率为2.2%。

而且，更进一步通过季度数据可以得到2014—2017年度GDP增长率分别为2.8%、2.0%、2.1%和2.1%。四年的GDP年平均增长率为2.3%，因此，在没有重大外部环境变化和结构调整的情况下，未来四年俄罗斯的年均增长率为2.3%。

本文还利用该模型对俄罗斯未来2018—2025年更长期的经济增长趋势进行了预测，表7是通过该模型预测的2017—2025年的年度GDP。

由表7预测结果可以得出，该时间段的年度平均增长率大概为2.1%左右，这个结果要大大低于2009年之前的水平，但是需要指出的是由于模型精确度随时间的推移下降。因此，该结果还需要运用新的数据进一步地更新和完善，但不可否认的是俄罗斯经济低迷状态在没有大的结构调整和外部改善的情况下将会持续。

还需指出的是，2014年4月份国际货币基金组织对2014—2015年世界经济形势进行了预测，根据该结果，2014年俄罗斯GDP年增长率为2.0%，2015年的GDP年增长率为2.5%，从2014年来看的话，笔者的预测结果要略高于国际货币基金组织的预测，从2015年来看，要稍微低于其预测，但该预测的两年平均增长率基本符合笔者预测的未来四年GDP的2.3%的平均增长率，这也在一定程度上，验证笔者预测结果的准确性[11]。

五、结论和政策建议

本文使用时间序列预测分析方法，得到了一个较为精确的俄罗斯季度GDP的预测模型，并且使用该模型分析可以得出，在没有大的外部冲击和结构性变化的情况下，仅考虑GDP的自身运动规律，俄罗斯经济增长的低迷状态依然会持续下去，而且在长期内不会有很大的改善。俄罗斯经济增长形势依然严峻。

俄罗斯要想摆脱这种经济的低迷状态，就需要注重发展内需，降低进出口贸易在GDP中所占的比重，俄罗斯是一个典型的外向型经济国家，2013年出口额占GDP的比重达到1/4，这使得俄罗斯经济很容易受到外部经济环境变化的影响。2008—2009年的世界性经济危机，很大程度上说明了这一问题[12]。因此俄罗斯未来经济发展在注重对外贸易的过程中，强调发展内需的重要性是很重要的。

要加大发展高科技产业，增加出口产品的科技含量，目前俄罗斯出口产品中原材料占了接近70%，尤其是石油及石油制品占了接近一半，虽然这可以充分发挥俄罗斯的资源禀赋优势，但是并不利于俄罗斯经济的长期发展，使得俄罗斯经济面临着外部环境对原材料需求的限制，增强了经济的不稳定性。

俄罗斯要改变这种现状，最根本的还是要进行经济结构调整，发展创新型经济，改变单一的能源型经济结构，这是俄罗斯经济未来改革和发展的方向[13]。

参考文献：

[1] Замараев，Б.，Киюцевская，А.，Назарова， А.，Суханов，Е.Замедление экономи-ческого роста в России[J]. Вопросы экономики， 2013， （8）： 4-34.

[2] Мау， В.Между модернизацией и застоем： экономическая политика 2012 года[J]. Вопросы экономики， 2013， （2）： 4-23.

[3] Алексашенко，С.，Миронов，В.Д.Мирошничерко. Российский кризис и антикризисрый пакет： цели， масштабЫ， эффективность[J]. Вопросы экономики， 2011， （2）： 23-49.

[4] 邢国繁， 张曙霄. 资源禀赋、创新经济与俄罗斯未来 [J]. 东北亚学刊， 2012， （3）： 83-90.

[5] 苗华寿. 对当前俄罗斯经济持续低迷的评析 [J]. 东北亚学刊， 2014， （1）： 43-48.

[6] 杨伟传. 中国能源消费的 ARIMA 模型预测分析 [J]. 统计与决策， 2009， （11）： 71-72.

[7] 周广肃，Stata统计分析与应用[M]. 北京：机械工业出版社， 2011.

[8] 白雪梅， 赵松山. 关于对时序模型定阶方法的研究 [J]. 统计研究 ， 1999， （12）： 31-35.

[9] 谢佳利， 杨善朝， 梁鑫. 我国CPI时间序列预测模型的比较及实证检验 [J]. 统计与决策， 2008， （9）： 4-6.

[10] 朱颜杰， 樊顺厚， 雷怀英. 基于SARIMA模型的居民消费价格指数的预测 [J]. 统计与决策， 2014， （4）： 37-39.

[11] 国际货币基金组织. 2014年世界经济展望[M]. 莫斯科：盖达尔研究所出版社， 2014.

[12] 盖达尔经济政策研究所. 2013年俄罗斯经济形势与前景[M]. 莫斯科：盖达尔研究所出版社， 2014.

[13] 徐坡岭. 决定俄罗斯 2012 年后经济前景的两个关键因素： 社会政治改革与经济现代化模式 [J]. 辽宁大学学报（哲学社会科学版），2012， 40（1）： 140-149.

（责任编辑：巴红静）