响应面优化算法在建筑结构设计中的应用
焦 柯 梁施铭 贾 苏
(广东省建筑设计研究院, 广州 510010)
响应面优化算法在建筑结构设计中的应用
焦 柯 梁施铭 贾 苏
(广东省建筑设计研究院, 广州 510010)
本文介绍了响应面算法在建筑结构优化设计中的程序实现,包括响应面数据获取、数据拟合和数学规划。针对在实际工程应用中遇到的壁垒厚度、多峰值、初始点不在可行域等技术问题提出了解决办法。结合计算机技术,详细讨论了响应面算法的实现过程,并对程序进行验证,说明响应面算法适用于建筑结构优化设计。
响应面;建筑结构设计;编程技术;数学规划
1 前言
高层结构设计和优化的难点在于计算规模大,结构体系多样,需要满足的规范控制约束条件较多,不同物理量之间关系错综复杂,同时需要考虑抗震构造要求。响应面算法作为数学分析与统计方法的结合物,能对多变量多约束的大型工程问题进行拟合和分析,非常适用于计算量大并且变量关系复杂的工程优化问题。工程师不仅能透过这种智能的分析方法看到各变量的相互作用关系,也能得到各类设计指标对于变量的敏感度,并基于结构设计概念,通过优化程序自动实现结构调整。在此过程中工程师也能对结构有更深入的认识。响应面算法在工程优化的应用范围和作用越来越大。1960年,Schmit将数学规划引入到结构优化领域中。1998年Roux等对两杆、三杆和十杆的桁架结构进行优化,发现试验点的数量和位置对响应面精度有较大影响,而且对设计区域大小比较敏感。2006年隋允康等将中心复合和单纯形法引入到桁架截面优化中[1]。
目前响应面算法在结构分析中的应用研究多数着重于钢结构的分析上,对于混凝土结构的应用还不多。随着现代计算机技术的发展,通过响应面分析法与计算机技术的结合,实现对复杂的混凝土结构进行优化分析具有十分重要的意义。国外某些通用软件(如HyperStudy)能对各种结构工程问题进行响应面分析,但国内还未见类似软件。本文通过编程将响应面算法应用到混凝土结构设计优化中,能快速得到混凝土结构优化方向,提高设计优化效率,及节省建材,相比通用软件HyperStudy具有针对性强、效率高,并且更加适用于结构设计专业等优势。
2 响应面算法的编程实现
一个结构设计优化问题由设计变量、优化目标和约束条件组成。因为响应面算法是一种统计学与数值方法结合的算法,所以对于实验数据的数量和质量会显得比较敏感,通过尽可能少的实验次数,获得尽可能高质量的实验数据,能提高一个算法流程的效率。本文结合结构设计专业,设计数据实验方法。获得实验数据以后,便可以对目标和约束进行显式近似拟合,建立优化模型,从而为下一步的数学规划提供条件。
2.1 数据拟合方法
在计算机编程中,要对响应面有一个统一的输出和表达格式,这样有利于数据处理和分析。假设采用了二次响应面,并通过用向量来表达响应面的方式,对数据进行处理和运算。首先规定二次响应面的统一表达方式,如式(1)所示:
(1)
式(1)中对应各变量(包括线性项,交互项以及二次项)的系数用向量A来储存,代表一个响应面。规定了系数顺序之后,把所得n次实验数据,代入式(1)当中,将变量值统一放在矩阵X中,并改用矩阵表达,式(1)可改写为式(2)。
Y=XA
(2)
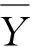
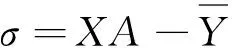
(3)
以系数向量A为变量,式(4)对误差平方求导,可求误差的平方最小值,从而推出式(5)系数向量[1]:
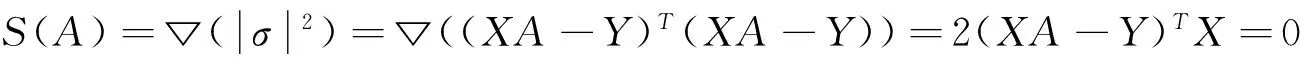
(4)
A=(XTX)-1XTY
(5)
为了验证拟合程序的准确性,通过表1对自定义方程与拟合方程进行对比,拟合方程采用全因子试验,生成试验数据。从表1中3个例子里可以看出对于3次方程,用2次曲面模拟的效果不太好,拟合结果是线性方程,而对于2次多项式方程,拟合出来的方程是与原方程一模一样的。对于4次方程,图1是自定义方程曲面,图2是拟合方程曲面,两者特征基本一致。

表1 自定义方程与拟合方程对比
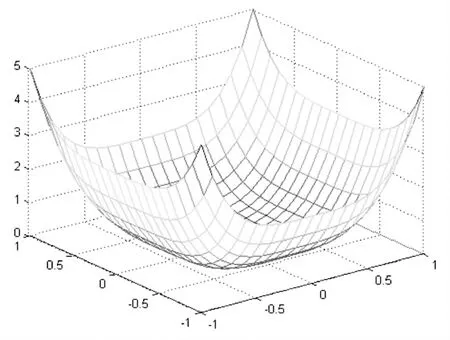
图1 自定义方程曲面
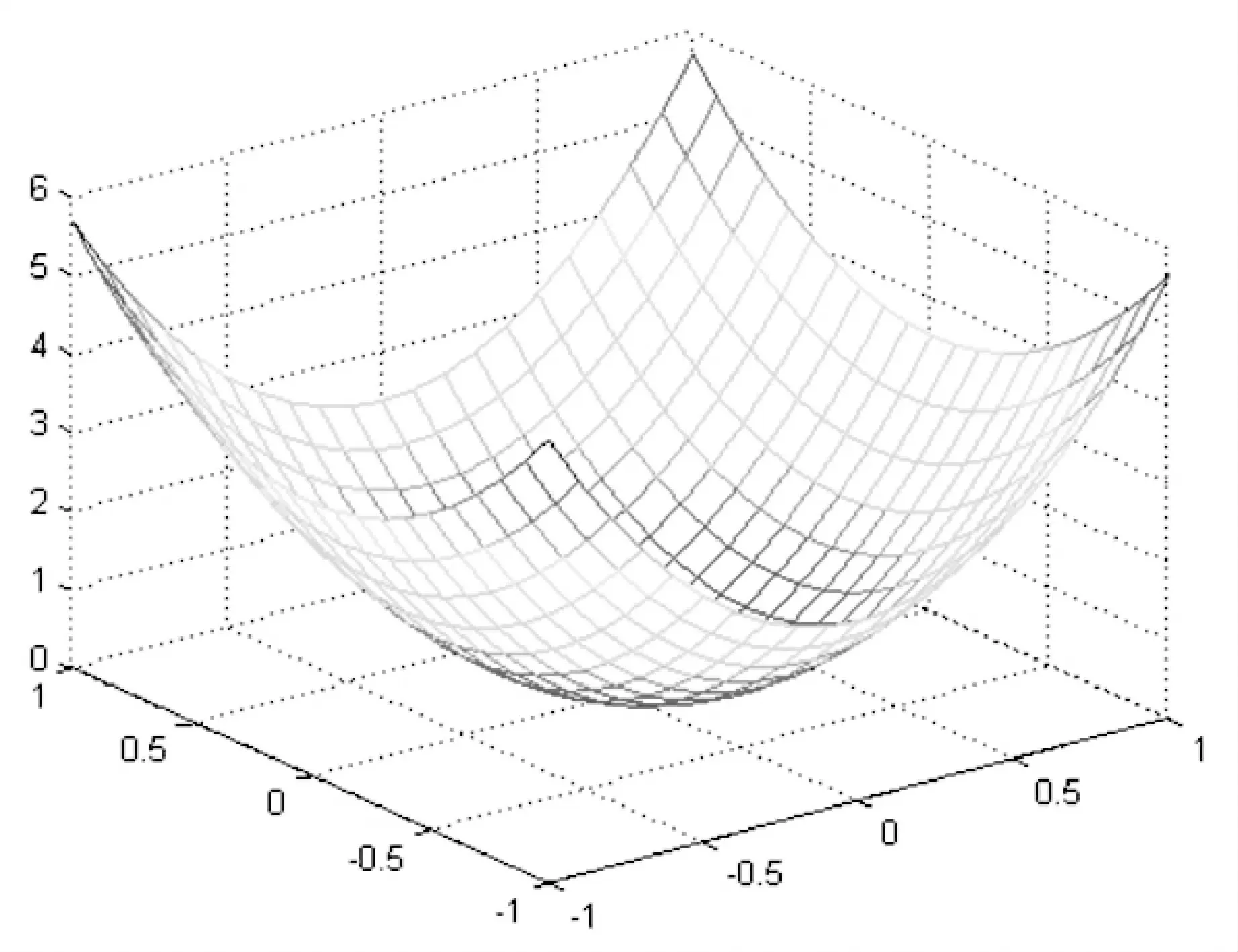
图2 拟合方程曲面
2.2 二次规划
本文中二次规划主要采用内点法,即在可行域内选取一个初始点,并在可行域边界上设置一道屏障,当迭代过程靠近可行域的边界时,新的目标函数数值迅速增大,从而在边界处斜率陡然变大,程序就停止往边界搜寻,而转往其他下降方向搜寻。假设有目标函数f(X),同时有不等式约束集g(X)≥0,搜寻目标函数的最小或最大值,构造新的函数形式,如式(6)所示:
(6)
3 二次规划中难点分析
3.1 壁垒厚度问题
内点法通过构造罚函数来控制每个迭代点都落在可行域中,然而在编程操作上,由于涉及到迭代步长的问题,程序可能会因为步长过大,跨过约束,从而造成无法收敛或在不可行域内迭代等问题。
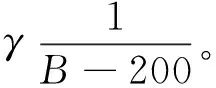
针对此问题,本文使用了阶级函数的方法,也就是一旦变量越过边界,函数会自动取一大值(如9999)形成壁垒。同时,当迭代点仍在可行域内时,保留罚函数形式,而只当变量刚好等于或已越过边界时,才会自动取大值,这是为了使函数靠近约束时,需要有一个平滑过渡,而不会有函数值突变。
3.2 数值求导问题
函数导数为0是程序迭代终止其中一个条件,说明函数已经处于局部极值,算法便会停止迭代。然而,如果变量已经非常接近边界,虽然边界处存在平滑山谷,但由于步长问题,数值求导的其中一点可能落在壁垒上,使得导数非常大,故而无法收敛。
对此,程序采用了邻域法来判断一个点是否局部最大或最小,也就是在x1, x2…. xn的前后方向,求函数值,若均比此点的值大或均比此点的值小,说明达到了极值点,停止迭代。
3.3 多峰值问题
对于多峰值曲面,由于局部极值点不一定等于全局最优点,存在不同起始点收敛到不同点的问题。一种比较有效的方法是采用截平面的方法。就是在每次求得局部最优点的时候,以该值为一个阀值,对响应面进行修剪,建立新的约束条件,然后再重新找起始点进行运算。本文采用二次响应面,故以二次曲面为例。具体方法是对每个变量进行二次修剪,以xk为变量,其他变量保持不变,然后在该维度上求出与此值相等的对应点,式(7)、式(8)、式(9)分别是单维度的常数项、线性项及二次项系数,解二次方程后看对应点是否落在可行域上,如果是,判断是否可以继续搜索寻找最优点;如果不是,说明此点是全局最优点,停止迭代。这样通过解二次方程,每次可以在单变量的一维空间里进行修剪。
a=akk
(7)
(8)
(9)
3.4 起始点不在可行域问题
变量的初始值可能落在可行域外,一旦初始点落在不可行域中,如果罚函数的值均只是一大值(如上文的9999),导数却是0,不会诱使搜索往可行域走,程序便会停止迭代。
传统内点法规定每一个迭代点均落在可行域中,本文对罚函数进行适当修改,使得阶级函数在大值基础上再递增,离边界越远,罚函数越大,这样既保留了起始点在可行域内的运动特征,也能让起始点落在不可行域时让其滑回到可行域内。本文采取的策略就是以离约束函数的距离(当约束函数值小于0时,求约束函数的绝对值)为标准,绝对值越大,说明偏离越大,罚函数的值就越大,从而人工制造一个负梯度,让点滑回到可行域。
3.5整体效应问题
式(5)表达式是通式,也就是不但适用于二次响应面,同时也适用于线性或高次响应面,结构设计中的变量众多,考虑到计算效率问题,一般采用线性响应面。假设采用线性响应面,如果问题含有n个变量,则需要做n+1次实验,但从结构设计专业来看,结构主要问题通常由三个方面引起,第一是整体刚度不足或过大,结构过柔或过刚,其次是平面内结构刚度或质量分布不均匀,造成结构扭转或其他问题,第三则是不同层之间刚度突变或不均匀,使得水平力无法传导。针对这三方面问题的优化,简单的线性响应面无法考虑多变量的交互作用,也就是说当结构整体刚度不足,需要多个变量同时增大或减小时,一般线性响应面无法得出优化方向。针对此问题,本文在常规线性实验完成后,增加一次整体效应实验。通过多个实际算例的验证,此方法能有效解决一般线性甚至高次响应面无法得到的整体优化效果。
4 算例
某10层框架结构的计算模型如图3所示。地面以上共10层,屋面高度34.6m,首层平面见图4所示。首层柱构件尺寸为600×800mm、600×600mm,主要梁构件尺寸为300×700mm、200×600mm。

图3 结构三维模型
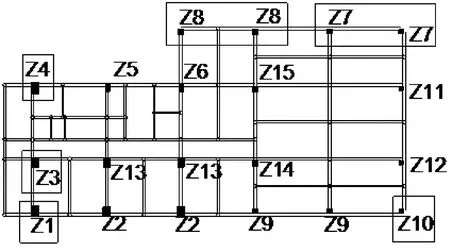
图4 首层结构平面布置图
结构前三个周期分别为1.486s(X向平动)、1.437s(Y向平动)、1.150s(扭转),扭转效应明显,结构楼层最大位移比为1.5。整体结构偏刚,X、Y向地震最大层间位移角分别为1/986和1/872。按照框架结构规范要求,取结构刚度比、承载力比和周期比作为约束条件,结构X和Y向最大层间位移角1/550为目标进行优化。
限于篇幅,只选取敏感度最高的前6个分组进行说明。这6组构件在图4用方框标出。表2列出各变量敏感度及优化结果,表中组号与图4中柱号对应。每组均有宽高两个变量共12个变量。表中变量敏感度采用初始敏感度除以所有变量的敏感度平方和计算得到,后两列是变量的初始值和优化后的数值。
本结构由于首层刚度分布不均匀,造成Y向位移比较大,对于Y向位移比,敏感度最大的五个变量依次为:1~2标准层组1柱高、组4柱高、组3柱高、组7柱高、组8柱高、组10柱高。其中组1、3、4组柱截面对Y向位移比呈负相关,组7、8、10组柱高对Y向位移比呈正相关,意味着组1、3、4组柱高增大,Y向位移比减小,而组7、8、10组柱高增大,Y向位移比增大。表2可见左侧角柱截面增幅较大(如组1、组4),原因是结构左侧刚度较弱,导致结构扭转效应较大,而增大左侧角柱能最有效提高结构抗扭刚度,故1、4组柱高敏感度最高。
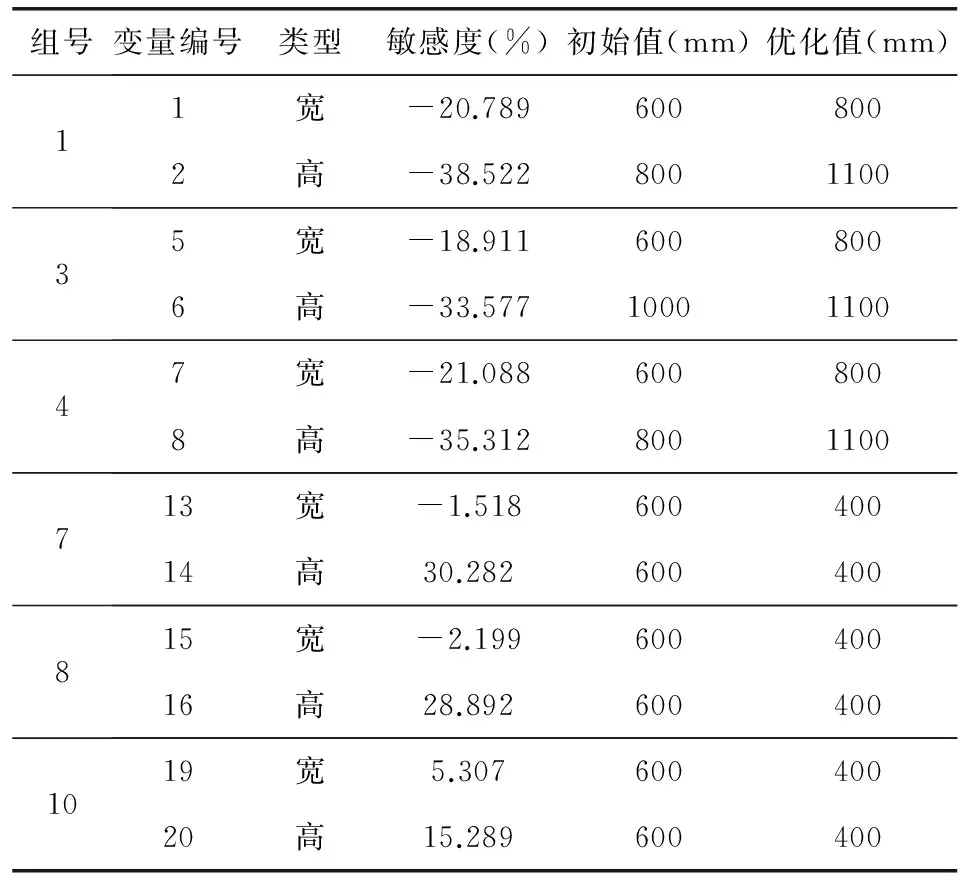
表2 各变量敏感度及优化结果
优化前后结构总体指标见表3,可见优化后X、Y向地震位移角分别为1/658和1/747,比优化前明显增大,解决了整体刚度偏大的问题,同时首层位移比降为1.18,显著降低了扭转效应。
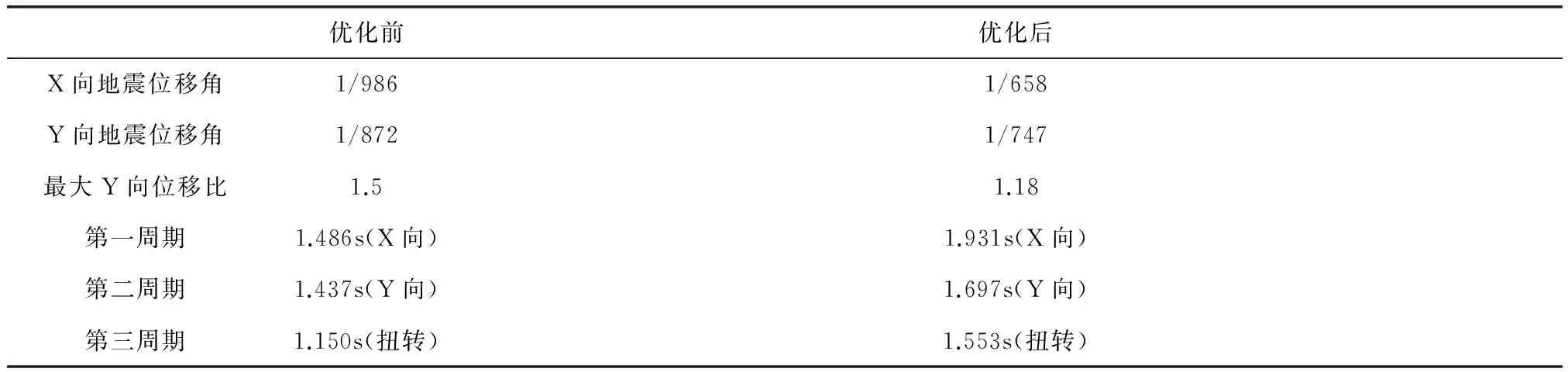
表3 优化前后总体指标
5 小结
(1)本文采用的响应面算法可用于建筑结构的设计优化计算,能直观地揭示多变量与目标之间的关系,同时收敛性好。
(2)传统内点惩罚法规定每个迭代点都需要在可行域内,本文对其进行了适当修改以适应建筑结构特点,无论初始值在可行域上或者不可行域上,都能搜寻到最优点。
(3)内点法中镶嵌的梯度法,能够用其他无约束的优化方法替代,例如共轭梯度法或者牛顿法,针对不同情况程序能够自动选择合适的算法,从而提高算法效率。
(4)修剪平面的方法效率高,因为这种方法不用考虑变量之间的交互作用,而是对各变量分开修剪。即使优化问题中有100个变量,也只是进行一百次修剪运算,效率较高。
(5)通过对某框架结构进行优化,达到了节省材料,提高抗震性能的目的,验证了响应面算法能应用于实际建筑结构优化设计。
[1]隋允康, 宇慧平. 响应面方法的改进及其对工程优化的应用[M]. 北京:科学出版社, 2011.
[2]马昌凤. 最优化方法及其Matlab程序设计[M]. 第一版. 科学出版社, 2010.
Application of Respond Surface Method in Structural Design
Jiao Ke,Liang Shiming, Jia Su
(TheInstituteofArchitectureDesign&ResearchofGuangdongProvince,Guangzhou510010,China)
Implementation of respond surface method in structural design is depicted in this article, including data experiment, data fitting and mathematical programming. Difficulties encountered are discussed as well, and solutions for problems caused by thin restricted barrier, multi-peak values and iteration in infeasible space are introduced. Details of the implementation are described with programming techniques. Feasibility is tested by a frame structure to verify that respond surface method is adapted to structural optimization design.
Respond Surface; Building Structural; Programming Techniques; Mathematical Programming
焦柯(1968-),男,教授级高工。主要从事结构分析软件研发和复杂结构计算分析工作。
TU311·4;O221
A
1674-7461(2015)01-0065-04

