不完全信息下基于随机抽样的群组评价法*
闫英等

摘 要:针对不完全信息下的群组评价问题,借鉴D-S证据理论的表达方式和思想,通过计算专家评价意见间的相似度矩阵,得到专家意见的客观权重,以此为依据对不完全信息进行融合,根据融合后的信息构造评价对象的累积分布函数,采用Monte Carlo随机抽样法得到最终的评价值,对评价对象进行排序。实例分析表明新方法正确、有效,且能较好的保留专家原始评价信息,得到更为客观的评价结果。
关键词:不完全信息; 群组评价; 随机抽样; D-S证据理论; 证据融合
中图分类号:N945.25 文献标识码:A 文章编号:
A Group Evaluation Method Based on Random Sampling under Incomplete Information
YAN Ying1, SUO Bin2, YUAN Ming1, GAN Mi3
(1. School of Economics and Management, Southwest University of Science and Technology, Mianyang 621010;
2. China Academy of Engineering Physics, Mianyang 621900, China;
3. School of Traffic Transportation & Logistics, Southwest Jiaotong University, Chengdu 610031, China)
Abstract: Aiming at group evaluation problem under incomplete information, a new method based on random sampling was proposed. Drawing on the expressment and thoughts of D-S evidence theory, similarity matrix between each two experts opinions was calculated to determine the objective weights of experts opinions, with which imcomplete information were fused. Cumulative distribution functions of evaluation objects were constructed based on fused information. Monte Carlo sampling was used to get the final values of objects, and then objects were sorted according to these values. Example shows the effectiveness and correctiveness of the new method. With this method, raw information in experts opinions are retained, and the evaluation results are more obejective.
Key words: incomplete information; group evaluation; random sampling; D-S evidence theory; evidence fusion
引言
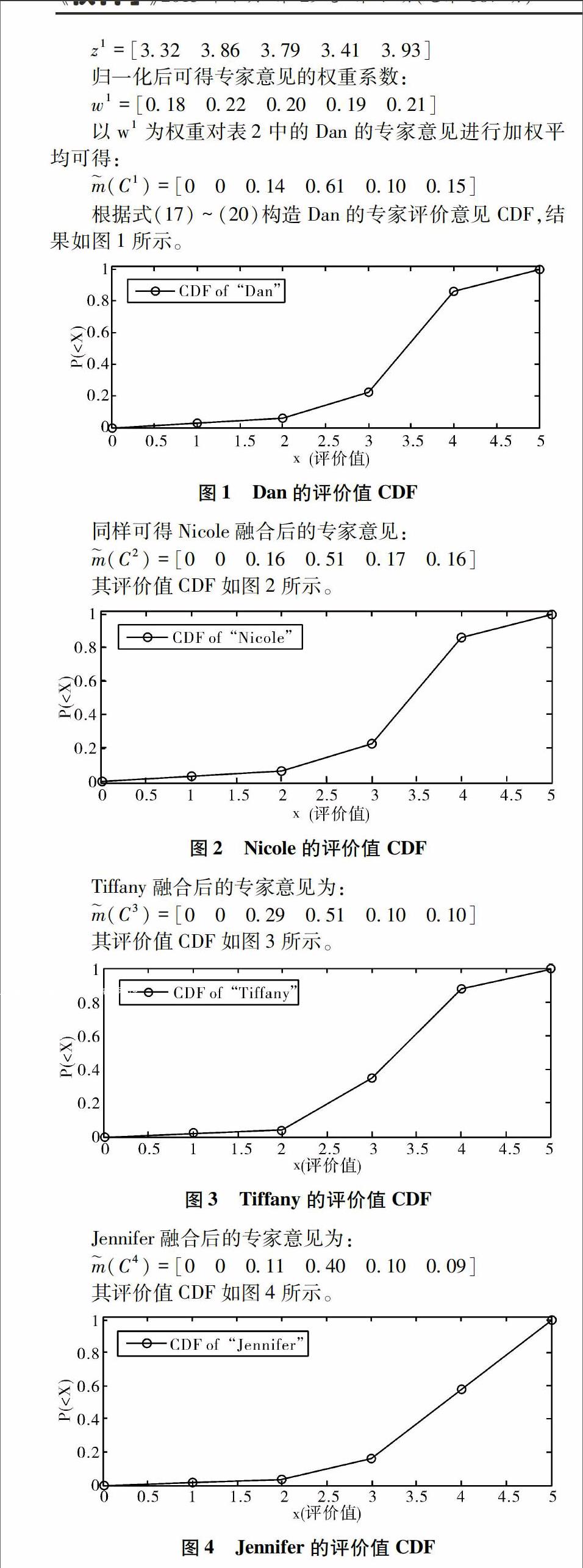
在实际的群组评价过程中,由于决策者自身知识和经验的局限性、时间的紧迫性,在面临复杂评价问题时,往往存在评价信息不完全的现象。例如,对于几个不同类型的项目进行投资风险评价,从中选择一项风险小、前景好的项目进行投资,不同的决策者可能仅对其中一两个项目涉及的行业比较熟悉,其他项目并不熟悉,但仍要做出评价,此时决策者往往倾向于对不熟悉的项目给出不完全评价信息。由于不完全信息评价问题有着重要的实际应用价值,近年来成为决策和评价领域的热点问题[1~11],其中基于D-S证据理论的方法受到了国内外学者的广泛关注[5~11]。文献[5]、[6]将D-S证据理论与AHP法相结合,通过AHP法求解判断矩阵的特征向量,将决策者的不完全信息转化为证据理论下的基本概率分配,进而采用Dempster规则对信息进行融合;文献[7]、[8]主要针对权系数不完全确定且方案的部分准则值位于两个语言等级之间的情况,提出了D-S证据理论融合决策信息、构造非线性规划模型的方法计算各方案的排序;文献[9]、[10]采用D-S证据理论将专家信息融合,并将融合后的信息转化为区间数,利用区间数排序做出最终的决策;文献[11]针对评价信息为定性、定量信息混合情况下的不完全信息多属性决策问题,提出了先利用信息熵原理确定专家的客观权重、再利用D-S证据理论集结多源信息的方法,对方案进行排序。
虽然基于D-S证据理论的不完全信息群决策、群组评价方法已有较多研究,但仍然存在不足。例如,文献[7]、[8]在信息融合时认为专家意见的权重相等,没有考虑到不同专家知识、经验等不同引起的差异化;文献[9]、[10]将融合后的信息转化为区间数的过程会损失较多有效信息,可能会影响最终决策的准确性;文献[11]利用D-S证据理论的信任函数和似然函数构造了评价对象的直觉模糊信任区间,再根据区间数排序的可能度公式得出最终的排序,该方法有一定的合理性,但构造的直觉模糊信任区间跨度过大,使得评价结果的可信度较低。此外,由于D-S证据理论的核心——证据合成规则在多源信息高度冲突的情况下存在缺陷,有可能得到有悖常理的结果[12~14],因此关于高冲突证据的合成规则目前仍然是国际上研究的热点问题[12~16],至今仍没有一个统一的、公认的方法,而文献[5]~[11]无一例外在决策信息融合时采用了D-S证据合成规则,当决策者的意见高度冲突时无疑会影响到评价结果的准确性。
为此,本文借鉴D-S证据理论的表达方式和基本思想,通过计算相似度矩阵得到专家评价意见的客观权重,进而对专家信息进行融合。在信息融合时,为避免信息损失和高度冲突意见合成带来的不利影响,本文将不采用D-S证据合成规则,最大限度的保留原始信息。最后,根据融合后的信息构造评价对象的累积分布函数,通过Monte Carlo随机抽样得到最终的评价结果。
4 结论
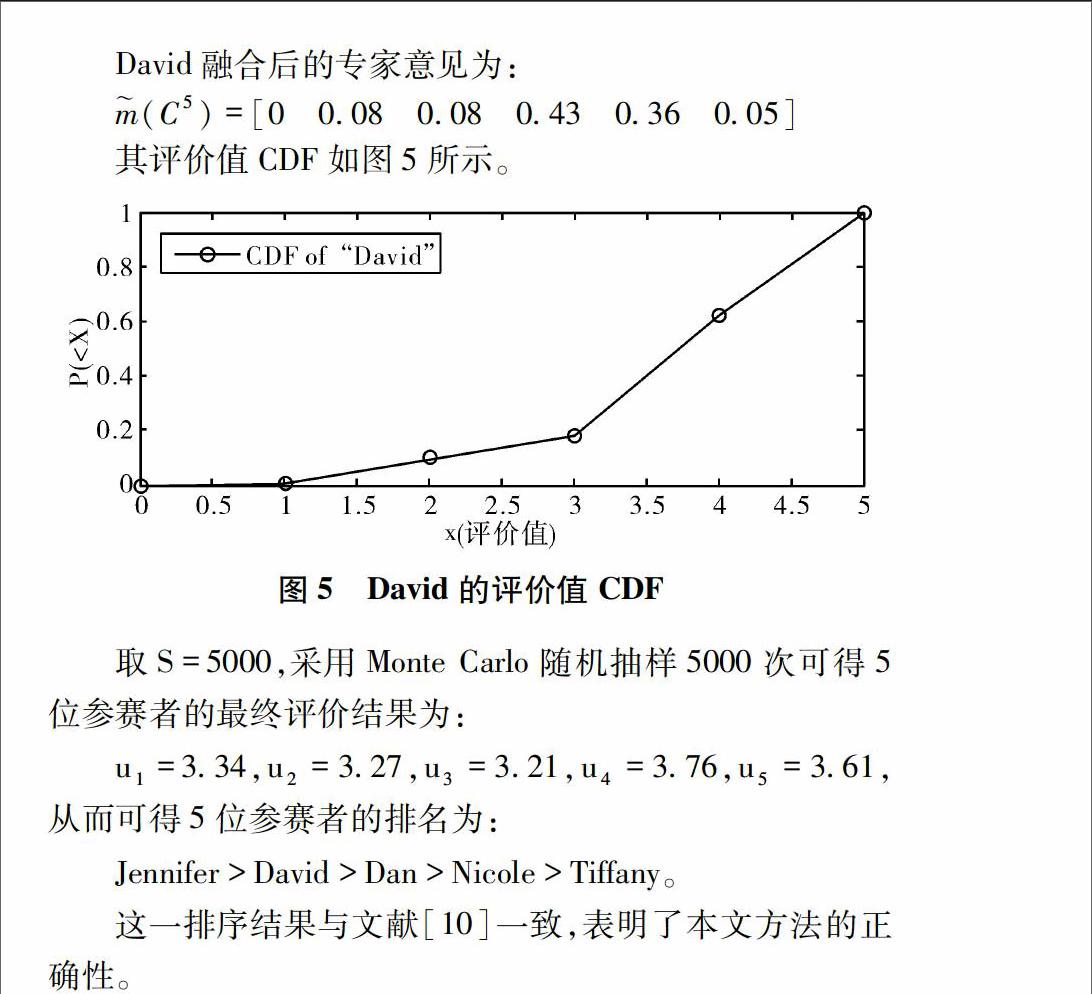
本文针对专家评价意见存在缺失的不完全信息下的群组评价问题,借鉴D-S证据理论的表达方式和思想,通过计算评价意见之间的相似度矩阵确定专家意见权重、对专家评价意见进行融合,进而构造各个评价对象的累积分布函数,通过Monte Carlo随机抽样得到各个对象的最终评价值,从而对评价对象进行排序。实例分析结果表明,本文方法正确有效,且能较好的保留专家原始评价信息,得到更为客观的评价结果。另外,基于随机抽样的方法简洁明了、易于计算机程序实现,因此便于在各类实际评价、决策问题中推广,具有广泛的应用价值。
另外,当评价问题更为复杂、群组意见的不确定性更大时,将可能引入多区间概率的形式来表达专家的意见。如何在多区间概率形式、不完全信息下进行群组评价,将是下一步的重点研究方向。
参考文献:
[1] Jacek S. Multi-criteria group decision making under uncertainty with application to air traffic safety [J]. Expert Systems with Applications, 2014, 41(16): 7406-7414.
[2] 李金鹏, 岳超源, 李武. 一类基于优势关系的不完全信息多属性决策方法[J]. 控制与决策, 2013, 28(2):229-234.
[3] 程铁军, 吴凤平, 李锦波. 基于累积前景理论的不完全信息下应急风险决策模型[J]. 系统工程, 2014, 32(4):70-75.
[4] 汪新凡,王坚强,杨小娟. 基于二元联系数的信息不完全的群决策方法[J]. 管理工程学报, 2014, 28(1):202-213.
[5] Bynon M. DS-AHP method: a mathematical analysis, including and understanding of uncertainty [J]. European Journal of Operational Research, 2002, 140:148-164.
[6] Hua Z S, Gong B G, Xu X Y. A DS-AHP approach for multi-attribute decision making problem with incomplete information [J]. Expert Systems with Applications, 2008, 34:2221-2227.
[7] 王坚强. 基于证据推理的信息不完全的多准则排序方法[J]. 系统工程学报, 2006, 21(4):419-423.
[8] 王坚强.一种信息不完全确定的多准则语言群决策方法[J]. 控制与决策, 2007, 22(4):394-398.
[9] 梁昌勇, 张恩桥, 戚筱雯等. 不完全信息下基于证据推理的竞争对手分析[J]. 系统工程, 2010, 28(2):44-48.
[10] 郭亚军, 姚爽, 黄玮强. 基于变权的语言评价信息不完全的群组评价方法[J]. 控制与决策, 2009, 24(9):1351-1355.
[11] 梁昌勇, 张恩桥, 戚筱雯等. 一种评价信息不完全的混合型多属性决策方法[J]. 中国管理科学, 2009, 17(4):129-132.
[12] Haenni R. Are alternatives to Dempsters rule of combination real alternatives [J]. Information Fusion, 2002, 3(4):237-239.
[13] Si L, Wang Z B, Tan C, et al. A novel approach for coal seam terrain prediction through information fusion of improved D-S evidence theory and neural network [J]. Measurement, 2014, 54(7):140-151.
[14] Mehena L, John K, Olivier C, et al. New distances between bodies of evidence based on Dempsterian specialization matrices and their consistency with the conjunctive combination rule [J]. International Journal of Approximate Reasoning, 2014, 55(5):1093-1112.
[15] 刘哲席, 阳建宏, 杨德斌等. 基于信息总不确定度的冲突证据组合修正方法[J]. 电子与信息学报, 2014, 26(12):2909-2914.
[16] 陈圣群, 王应明. 区间值信念结构下冲突证据组合[J].系统工程理论与实践, 2014, 34(1):256-261.
[17] 李仕峰, 杨乃定, 刘效广. 基于熵和证据理论的项目复杂性模糊评价[J]. 管理工程学报, 2013, 27(1):121-127.
[18] Montserrat C, José M. Fuzzy aggregation operators in decision making with Dempster-Shafer belief structure [J]. Expert Systems with Applications, 2012, 39(18): 7138-7149.
[19] 朱春江, 唐德善. 基于古林灰色证据理论的农业产值因素分析研究[J]. 软科学, 2006, 20(4):16-18.
[20] 陈星光, 笪佳敏. 基于证据理论的全过程多级群决策模型[J]. 软科学, 2012, 26(5):132-135.
[21] A.P. Dempster. Upper and lower probabilities induced by a multi-valued mapping. Annals of Mathematical Statistics, 1967, 38(4):325-339.
作者简介:
闫英(1979-),女,西南科技大学经济管理学院讲师、博士,研究方向为物流系统规划与管理、决策分析。
通信地址:四川省绵阳市西南科技大学经济管理学院
邮编:621010
Email:yanying_527@163.com
电话:13558990352

