基于组合核函数相关向量机的体育成绩预测

刘 昊

0 引言

体育成绩预测可以反映体育项目运动成绩的变化态势，帮助学校、运动队、体育培训机构制定科学的训练方法，为运动员和教练提供有价值的参考意见，以促进体育教学和体育训练的改革，因此体育成绩预测一直是体育研究领域的热点[1]。

针对体育成绩预测问题，国内许多研究机构和科研院所都进行了广泛、深入的研究，涌现出了许多体育成绩预测模型。当前体育成绩预测主要分为两类：线性预测模型和非线性预测模型，线性预测模型主要包括多元线性回归分析、自回归求和滑动平均等[2]，取得了不错的应用效果，而体育成绩与多种因素有联系，各种因素之间又相互作用，导致体育成绩变化十分复杂，但是线性模型假设体育成绩一种周期性或上升的变化趋势，这与体育成绩实际变化特点不相符，应用范围具有局限性[3]。非线性体育模型主要包括神经网络、灰色模型、马尔可夫链以及支持向量机等[4]，它们对体育成绩与影响因子之间的变化关系进行拟合，它们以较高的精度逼近体育成绩变化函数，取得了比线性模型更高的预测精度。然而在实际应用中，这些模型也存在一定的缺陷，如灰色模型、马尔可夫链要求体育成绩与历史数据变化是相吻合的，而且体育具有一定的非线性变化特点，这样假设常常不能够满足；当学习本数量有限时，神经网络的预测精度比较低，而当学习本数量比较大时，却易出现“维数灾”、“过拟合”等问题；支持向量机的泛化能力好，但是学习速度比较慢，当训练样本比较大时，建模时间十分惊人，实际应用价值差[5,6]。相关向量机(RVM)是一种新发展起来的非线性学习算法，是一种基于高斯过程模型的稀疏概率模型，解决了神经网路“过拟”等不足，同时具有较好的学习效率，避免了支持向量机学习过程耗时的缺陷，在网络流量、陀螺仪随机漂移补偿等非线性预测领域取得了成功的应用[6]。然而相关向量机作为一种新型的学习算法，在应用实际中，核函数选择十分关键，当前还没有一个统一指导理论，全凭经验进行设置，影响相关向量机的预测性能[7]。

结合体育成绩复杂的变化特点，利用相关向量机的非线性建模优势，建立了一种基于组合核函数相关向量机的体育成绩预测模型，并通过多个预测实例对模型的性能进行综合测试与分析。

1 体育成绩预测的原理

设收集到的体育成绩组成一个序列{y1,y2,…,yn}，由于当前体育成绩yi与其影响因子有关，它们之间存在一定的非线性变化关系，即有：

式中，d为输入向量的嵌入维数，其通过主成分分析进行选择；f()为非线性映射函数。

对式(1)进行分析可知，在体育成绩建模过程中，非线性映射函数f()的拟合是关键，当前拟合该函数的算法相当多，本文采用相关向量机进行逼近非线性映射函数f()，建立体育成绩预测模型。

2 组合核函数相关向量机的体育成绩预测模型

2.1 相关向量机算法

式中，ωi为噪声。

可以通过核函数K(x,xi)的线性组合形式描述相关向量机，即

其中，w=[w0,w1,…,wN]T为权值向量。

相关向量机的概率模型可以描述为：

引入一个超参数β，将整个训练样本数据组的似然函数表示为：

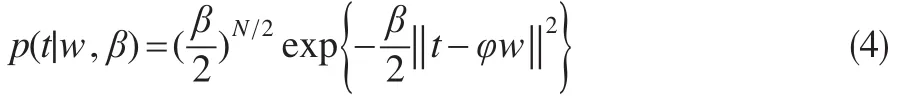
其中t=[t0,t1,…,tN]T，φ∈RN×(N+1)为设计矩阵。

将wj的先验分布定义为满足0为均值，为方差的高斯分布，表示为：

其中，a=[a0,a1,…,aN]T为超参数。

利用式(4)和(5)，根据贝叶斯公式即可得到w后验分布的数学表达式：

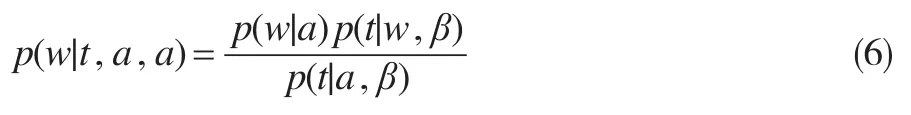
式中，p(w|a)与p(t|w,β)皆为高斯分布。

p(t|a,β)中不含有w,则可将其看作一个系数，因此可写为：

式中，∑是协方差矩阵，μ是均值向量，它们分别为：

其中，A=diag(a0,a1,…,aN)。

w的后验分布就必须对β和aj进行优化，可得到aj和β的计算公式：

其中，μj为μ的第j个元素，∑jj是矩阵∑的第j个对角元。

重复上述步骤进行相向量机训练，同时更新∑和μ，直到达到最大迭代次数，对于新输入的一组数据x*，其对应的输出为t*。

2.2 组合核函数的构建

在相关向量的体育成绩建模与预测过程，首先要解决的一个问题就是核函数的选择。由于任何函数均可以作为相关向量机的核函数，然而不同核函数可以建模不同类别和性能的相关向量，目前核函数众多，不同核函数均有各自的优缺点，当前相向量机的核函数主要为多项式和径向基核函数，它们分别定义如下：

多项式核函数泛化能力比较强，但学习能力差，径向基核函数刚好相反，学习能力强，泛化能力差，利用两者的优势，构造一种组合核函数，具体形式如下：

式中，ρ1和ρ2为两个函数权重。

2.3 组合核函数相关向量机的体育成绩建模步骤

(1)首先进行体育成绩历史样本收集，并采用主成分分析选择输入向量，建立将体育成绩的训练集和测试集，然后根据式(17)对它们进行归一化处理。

式中，xmin和xmax分别为最小和最大值函数。

(2)分别令ρ1=1，ρ2=0和ρ1=0，ρ2=1计算多项式核函数和径向基核函数最优核参数。

(3)根据多项式核函数和径向基核函数最优核参数，采用粒子群算法对最优ρ1和ρ2的值进行确定。

(4)根据最优组合核函数参数，采用训练集对组合核函相关向量机进行训练，建立基于组合核函数的相关向量成绩成体预测模型模型，并对测试集进行预测，输出体育成绩的预测结果。

综合上述可知，基于组合核函数相关向量机的体育成绩预测模型工作流程如图1所示。

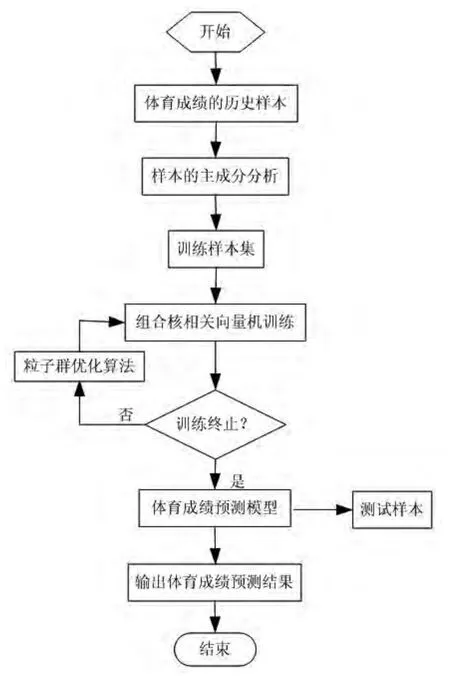
图1 体育成绩的组合核函数相关向量机的工作流程

3 组合核函数相关向量机的体育成绩预测实例

3.1 数据来源

本文数据采用中南财经政法大学的1000个学生（女生）立定跳远成绩(y)，影响因子为：身高(x1:cm)、体重(x2:kg)、肺活量(x3:ml)、50米跑(x4:s)、坐位体前屈(x5:cm)、800米跑(x6:s)、一分钟仰卧起坐(x7:次)，部分数据见表1所示。

表1 立定跳远成绩与其影响因子的值

3.2 建立体育成绩的学习样本

表1中的身高、体重、肺活量、50米跑、坐位体前屈、800米跑、一分钟仰卧起坐之间影响，而且存在一定的重复消息，因此对它们进行主成分分析，影响因子的相关系数如表2所示，主成分方差累计贡献率如图2所示，从图2可知，前4个主成分的累计贡献率达到90%以上，因此可以选择这4个主成分作为立定跳远成绩预测模型的输入向量，从而建立立定跳远成绩的学习样本。

表2 影响因子的相关系数分析结果

图2 体育成绩的主成分方差累计贡献率

3.3 结果与分析

3.3.1 组合核函数相关向量机的预测性能分析

随机选择900个样本组成立定跳远成绩的训练集，对组合核函数相关向量机进行训练，并采用对粒子群算法确定最优的ρ1=0.45，ρ2=0.55，建立立定跳远成绩的预测模型，然后对100个立定跳远成绩测试样本进行预测，预测结果与预测偏差变化曲线如图3和图4所示，从图3可知，立定跳远成绩的预测值与实际值变化趋势十分相似，组合核函数相关向量机得到了十分理想的立定跳远成绩结果，同时从图4可知，立定跳远成绩的预测值与实际值之间的偏差比较小，而且预测偏差变化幅度也比较小，实验结果表明，本文将组合核函数相关向量机引入到立定跳远成绩预测中是可行的、有效的。

图3 组合核函数相关向量机的预测值与实际值拟合曲线

图4 组合核函数相关向量机的预测偏差变化曲线

3.3.2 与其它体育预测模型的性能对比

为了使组合核函数相关向量机的预测结果更具有说服力，选择自回归求和滑动平均、组合核函数支持向量机、RBF神经网络作为对比模型，并采用采用均方根误差(RMSE)和平均相对百分比误差(MPAE)进行衡量，它们定义为：

式中，n表示样本数。

自回归求和滑动平均、支持向量机、RBF神经网络和组合核函数相关向量机的RMSE、MAPE的值如表3所示。从表3知：

(1)ARIMA预测结果的RMSE、MAPE值均较大，这主要是由于ARMA假设立定跳远成绩是一种规律性的变化趋势，难以描述立定跳远成绩中的非线性变化趋势，导致预测的误差较大。

(2)RBF神经网络预测结果的RMSE、MAPE值也比较大，主要是由于RBF神经网络是一种基于经验风险最小化的学习算法，易出现“过拟合”、“欠学习”缺陷，不能有效建立准确描述立定跳远成绩变化特点的预测模型，而且预测结果极不稳定，有时偏差超过立定跳远成绩的实际应用要求。

(3)组合核函数支持向量机和组合核函数相关向量机预测结果的RMSE、MAPE相对较小，主要是由于它们均是基于结构风险最小化原则建模，较好的拟合了立定跳远成绩的变化特点，提高了立定跳远成绩的预测精度，预测结果更加理想，但是和组合核函数相关向量机预测性能要优于支持向量机，而且克服支持向量机的学习速度慢的缺陷，提高体育成绩的建模效率。

表3 不同模型的立定跳远成绩预测误差对比

3.3.3 组合核函数相关向量机的通用性测试

选择学生的50米跑成绩、（女生）800米跑成绩、（男生）1000米跑成绩、（女生）一分钟仰卧起坐成绩进行通用性测试，组合核函数相关向量机预测结果的RMSE、MAPE如表4所示。从表4可知，对于所有的体育成绩，组合核函数相关向量机预测的RMSE均比较小，而且MAPE的值控制在了5%以内，可以满足体育成绩实际应用要求。

表4 组合核函数相关向量机的不同体育成绩预测误差

4 结束语

为了对体育成绩进行准确预测，避免单一核函数的不足，建立了一种基于组合核函数相关向量机的体育成绩预测模型，实验结果表明，组合核函数相关向量机不仅获得了较好的体育预测精度，而且具有优良的通用性，为体育成绩预测提供了一种建模工具。

[1] 赵波.十项全能世界顶尖男子运动员成绩分析及预测研究[J].体育文化导刊,2013,3(3).

[2] 邓美兰等.奥运会男子十项全能前三名成绩的灰色预测模型的研究[J].数学的实践与认识,2009,(18).

[3] 孙群,刘国璧,程伟等.基于模糊神经网络的刘翔110m栏成绩预测[J].重庆科技学院学报(自然科学版),2011,10(2).

[4] 龙斌.基于支持向量机的刘翔110m栏成绩预测[J].天津体育学院学报,2009,24(4).

[5] 李征宇,闫生.神经网络模型在运动成绩预测中的应用[J].哈尔滨体育学院学报,2009,27(2).

[6] 马登武,范庚,张继军.相关向量机及其在故障诊断与预测中的应用[J].海军航空工程学院学报,2013,28(2).

[7] 杨柳,张磊,张少勋等.单核和多核相关向量机的比较研究[J].计算机工程,2010,36(12).