基于ELM的成本预测方法实证检验

朱 正，陶 岚

0 引言

会计成本预测一直是学术界比较关心的问题，不论企业的大小，在对企业生产，特别是进行新的产品研发和上线过程中，会计成本预测成为企业决策的重要参考，因此，关于会计成本预测也是学界一直研究的热点问题。通过对以往关于会计成本预测方法的研究和总结可以看出，首先，会计成本预测过程中影响因素众多，各因素之间的关联性很强，具有很强的非线性关系，因此简单的线性预测方法是不可行的，必须利用能有效反映各因素之间非线性关系的非线性预测方法，对会计成本预测的精度才会高；其次，所使用的预测方法，有人工神经网络方法，有模糊粗糙集成本预测方法，这些方法虽然能有效提升成本预测的精度，但是其共同特点是计算复杂，计算量大，不便于实际的应用。因此，构建一套新的简单、快速、又能反映会计成本预测中非线性关系是后期成本预测方法的主要研究和发展趋势。本文结合最新研究成果，利用最新提出的一种基于单隐层前馈神经网络的极限机器学习法（ELM），该方法既能反映出成本预测中各因素之间的非线性关系，还能有效提升成本预测速度，结构简单，因此，基于ELM的成本预测是最适合作为成本预测的模型。

1 极限学习机（ELM）建模原理

最近基于神经网络提出的一种新的极限学习机（ELM)通过随机产生隐曾结点参数,然后利用得到的外权决定输出，大大简化了传统神经网络复杂的迭代过程，使得在保证高精度拟合的基础上大大简化了运算过程。下面给出极限学习机的建模原理。

对N个任意确定样本 (xi，yi)，其中 xi=[xi1，xi2，…xin]Τ∈Rn，yi=[yi1，yi2，…yim]Τ∈Rm，标准的单隐层前馈神经网络(SLFNs)学习算法有个隐含结点，选取适当的激活函数g(x)，则根据神经网络的结构原理结构图为：

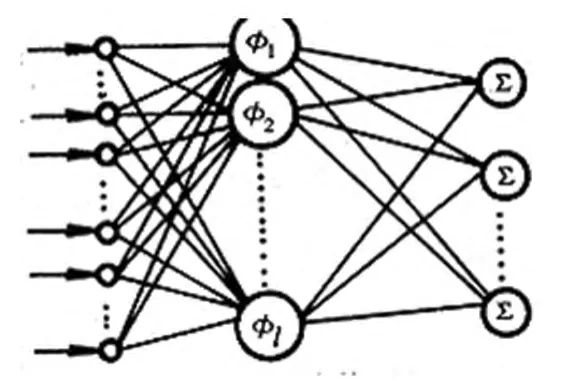
图1 单隐层前馈神经网络(SLFNs)结构图

其对应的神经网络的数学模型描述如下：

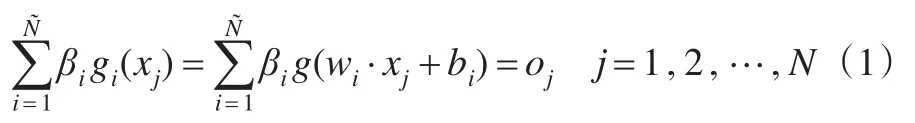
其中 wi=[wi1，wi2，…win]Τ∈Rn是第 i个隐含层结点和所有n个输入结点的连接权重向量，βi=[βi1，βi2，…βim]Τ∈Rm是第 i个隐含结点和所有m个输出结点的连接权重向量，并且常数bi是第i个隐含结点的阈值，其中wi·xj表示向量wi和向量xj的内积。

g(w1·x1+b1)β1+g(w2·x1+b2)β2+ …+g(w·x1+b)β=y1

g(w1·x2+b1)β1+g(w2·x2+b2)β2+ … +g(w·x2+b)β=y2

利用矩阵的形式将上面的方程进行简写，得到线性矩阵方程：

其中

H一般称为神经网络隐含层输出矩阵，其中H的第i个列是第i个关于输入x1，x2，…，xN的隐含层结点输出。

为了训练一个SLFNs，其实就是通过不断的学习训练，找到理想的向量和常数使得以下最优化函数有解：

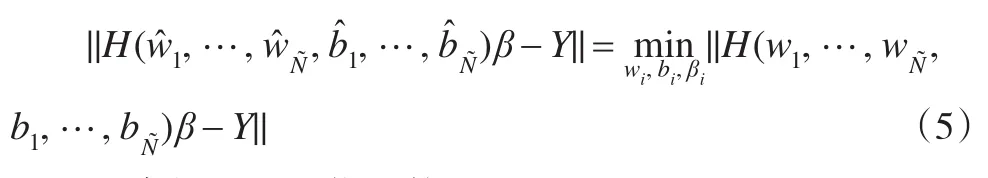
即求解以下最优函数：

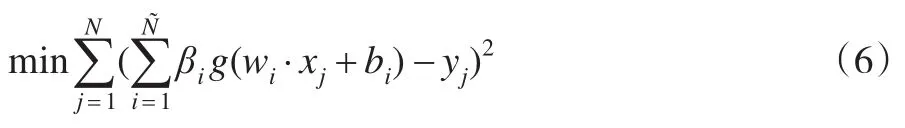
该函数的求解，通过证明，当给定加权向量wi和bi后，其最优解等价对线性方程组Hβ=Y求解。考虑到样本个数N和隐层结点数不同，因此，在对线性方程组Hβ=Y的求解过程中，可以采用广义逆的方法进行求解。

2 基于ELM的成本预测算法设计

通过以上的分析可以看出，极限学习机是基于单隐层前馈神经网络构建的预测模型，因此具有神经网络的非线性特性，但是通过最终的推导可以看出，最终ELM方法在对隐层权重的求解简化为对线性方程组的求解上，大大简化了预测的计算速度，下面基于ELM的原理，给出基于ELM的会计成本预测算法设计过程。

设对某企业的会计成本进行预测，选择L个时期内的企业成本历史数据为：

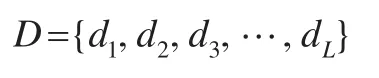
其中向量xi代表第i次随机选择成本历史数据所对应的时间，而yi则是第i次随机选择成本历史数据所对应的成本值。

③选定激活函数g(x)，计算隐含层输出矩阵H。

⑤预测：选择所要预测的时间，如预测未来p个时期内的企业会计成本数值，则选择

x*=(L-n+p+1，…，L-2，L-1，L，L+1，L+2，…，L+p)将基于ELM的预测值为：

语言不是独立的，是与社会文化相关的，因而语言表达方式存在差异。汉语是话题突出型语言，需说明的对象总是放在句子开头处，采用隐性连贯，句子间没有过多的连接词，短句之间靠整个话题维系；而英语是主语突出型语言，常采用主语-谓语的句式，采用显性连接，可用多种的连接手段表达时序和逻辑关系，复合长句是英语的一个主要特色。因此，汉英翻译时须做好语序的调整和句型结构的转换。

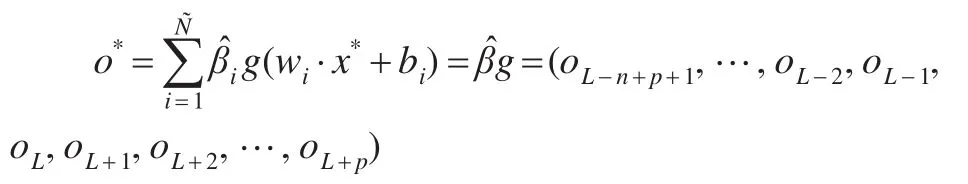
其中

则oL+1，oL+2，…，oL+p就是利用ELM得到的未来 p个时期内的企业会计成本预测数值。

3 基于ELM的成本预测实证检验

在对企业成本预测过程中，必须选择简单可据操作性的预测方法。某企业为了对企业的成本进行监测和控制，必须定期对企业成本进行预测，现在采集近20个时期的成本作为成本历史数据，建立企业的成本预测模型，采集到的成本数据如表1所示。

表1 某企业近20个时期内的成本预测数据 （单位：十万元）

首先构建训练样本集，在20组成本数据中，随机选择7组数据构成一个训练样本，共随机产生50个训练样本构成训练样本集：

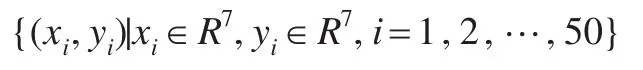
其中xi代表第i次随机产生训练样本中的时间序列构成的向量，yi代表第i次随机产生训练样本中的成本数值序列构成的成本向量，选取激活函数为高斯函数，即：

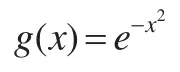
设定隐层结点个数为10个，随机产生加权向量值，随机给定偏置值bi（ i=1，2，…，10 ）为 ：b=(7.27，7.94， 1.36， 5.82， 2.97，4.15， 2.96， 6.83，4.54， 6.8)

表2 随机给出的加权向量矩阵

将随机产生的50个样本值 (xi，yi) ，(i=1，2，…，50)，随机给定的隐含层结点和所有输入结点的连接权重向量W（表2）、隐层结点偏置值b，激活函数g(x)=e-x2带入下式：

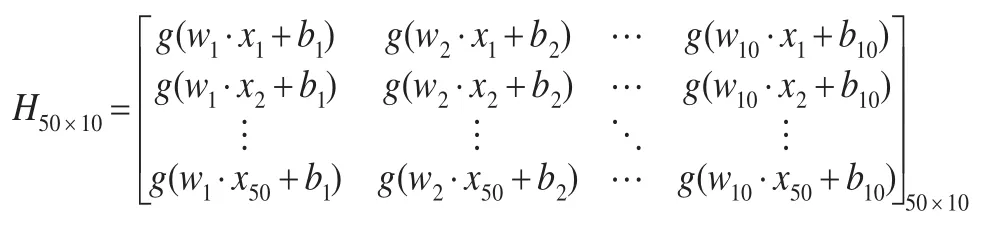
从而得到一个常数型的神经网络隐含层输出矩阵H50×10。将50个训练样本的输出成本向量排列构成成本输出矩阵：

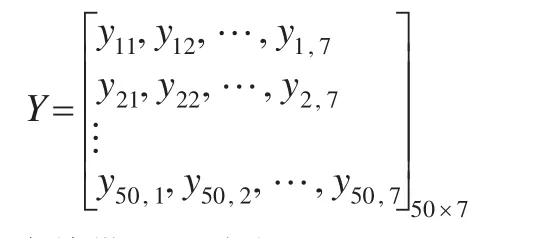
Hβ=Y

为了检验本预测模型的精度，选取验证序列对

xtest=(14，15 ，16，17，18，19，20)

ytest=（26.31，26.01，24.15，23.14，25.89，24.98，26.12）

将 xtest，w1，w2，…，w10，b 带入下式：

从而得到对成本预测数据的模拟值为：

通过计算实际成本数据ytest与模拟成本数据otest的平均误差为：

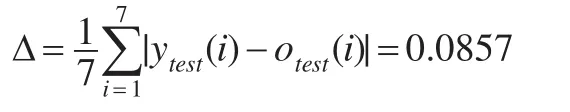
实际成本数据ytest与模拟成本数据otest的平均相对误差为：

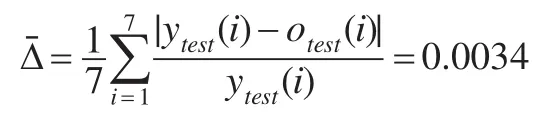
说明通过基于ELM方法训练出来的企业成本预测模型的拟合精度较高，因此，该模型是可以作为该企业的成本预测模型的。

为了预测未来连续三个时期内的企业成本，选择预测输入向量为：

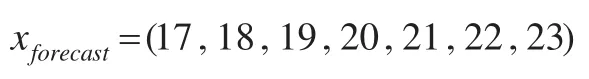
将 xforecast，w1，w2，…，w10，b带入下式：

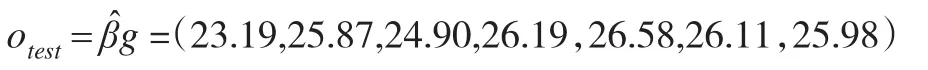
通过以上的基于ELM预测模型得到，未来三个时期内，该企业的成本预测结果为：

表3 某企业未来3个时期内的成本预测数据 （单位：十万元）

说明在第21个月内企业的会计成本将为26.58（十万元），22个月的企业会计成本为26.11（十万元）,第23个月的会计成本为25.98（十万元）。即表明该企业的成本在未来的使用中将会呈现减少趋势。

4 结语

成本预测从最初的定性预测方法为主到以数学模型为主的预测方法，考虑到成本预测过程中各影响因素的复杂性和多样性，使得成本预测呈现多样性和非线性，基于非线性的成本预测方法应该是未来成本预测的重心，本文对现有的非线性预测方法进行了分析，指出现有非线性预测方法的突出问题是模型复杂、计算量大，不利于成本预测模型的推广和实际使用，而本文所提出的基于极限学习机原理的成本预测方法，其模型简单，计算方便，易于掌握，且能反映出成本影响因素之间的非线性关系，因此，作为将ELM方法作为成本预测模型，能有效提升成本预测精度和使用范围。

[1] 刘崇欣.基于模糊粗糙集的模具成本预测方法[J].计算机集成制造系统,2012，(10).

[2] 訾书宇,魏汝祥,林名驰.成本预测系统中的自变量约简方法[J].统计与决策,2012，(18).

[3] 李敬.基于TOPSIS的成本组合预测方法及其应用[J].统计与决策,2013，(4).

[4] Huang G B,Zhu Q Y,Siew C K.Extreme Learning Machine:Theory and Applications[J].Neurocomputing.2006,70(1).

[5] Huang G B,Chen L,Siew C K.Universal approximation using incre⁃mental constructive feedforward networks with random hidden modes[J].IEEE Transactions on Convexincrementalextremelearningmachine NeuralNetworks,2006,17(4).

[6] Huang G B,Chen L.Convexincre Mentalex Tremelearning Machine[J].Neurocomputing,2007,70(1).

[7] Huang G B,Li M B,Chen L,et al.Incremental Extreme Learning Ma⁃chine With Fully Complex Hidden Nodes[J].Neurocomputing.2008,71(4).

[8] uangG B,Li M B,Chen L,et al.Enhancedr and Omsearch Base Dvncremental Extre Melearning Machine[J].Neurocomputing,2008,71(4).