数学化视角下的数量关系表征例谈
张敏

近日,看到朋友正在上六年级的儿子小朱的一份批改过的数学试卷,上面有这样一道题目引起了笔者的注意,如图1:
这是一道找规律的题目,要求学生能从简单情况入手,进行观察、比较、思考,进而发现小棒的根数与八边形的个数之间的数量关系,并能将这种关系以比较抽象的数学方式加以表征。题目中括号里填写的“8n-(n-1)”是小朱考试时写出的答案,很显然老师给他判了个“×”,后面是小朱订正后写出的答案“7n+1”,订正时在每一个图形的下面还标出了“8、15、22”几个数据。
于是我们有了下面一段对话:
笔者:你这道题怎么错了?
小朱:我的答案可能不简便吧。
笔者:为什么?
小朱:如果把8n-(n-1)的括号去掉后,后面的减号变成加号,再用8n减去n,就是7n+1了,这个答案比较简洁。
笔者:那你的8n-(n-1)这个答案是怎么想出来的?
小朱:从第二个图形开始就是八边形重合在一起了,2个八边形有1条边重合,3个八边形有2条边重合,以此类推n个八边形有n-1条边重合,n个八边形原来有8n条边,减去重合的n-1条边,那么就需要8n-(n-1)根小棒了。
笔者:你的想法很好啊,这个答案正好体现了你的思考过程。那老师所说的7n+1是从你的答案化简来的吗?
小朱:不是,老师是这样讲的:1个八边形是8根,2个八边形是15根,3个八边形是22根,小棒的根数是八边形个数的7倍多1,所以n个八边形就是7n+1根。
笔者:你觉得,老师的答案比你的答案好吗?
小朱:好。
笔者:老师讲的思考方法和你的相比,谁的好?
小朱:我的方法也挺好。要是我把答案化简一下就好了。
笔者:你觉得老师这样批改有道理吗?
小朱:应该有吧。
……
这一段对话引起了笔者的思考。从上述对话中可以看出,小朱对这道题的思考是完全正确的,他发现了图形的变化规律以及变化过程中小棒的排列特点,并且依据这种特点,很自然、很准确地表征了小棒的根数与八边形的个数之间的关系,显得水到渠成。然而教师却轻易地将孩子的答案判为错误,毫无疑问,教师的这种评判是不对的,这种误判折射出了我们很多教师在认识上的偏差。
一、 原生态表征与精致化表征孰高孰低
小朱所写出的答案8n-(n-1)可看成是一种对小棒根数与八边形个数之间的数量关系的原生态表征,它是在学生观察比较的基础上,独立探索、自主发现并表征出来的数量关系,反映出学生思维的原始性,它真实、自然地反映了学生的思维过程和对题中数量关系的理解,更多地体现了对思维过程的直接揭示;而从教师的角度理解,教师给出的答案7n+1可以看作是一种在学生原生态表征基础上的进一步精致化,更多地体现了对思维结果的形式化表达。
这两种表征方式在数学学习中都经常地、大量地存在着,它们之间是否存在孰高孰低的问题呢?
从表征的结果上看,它们都正确地揭示和反映了数量之间的本质联系;从表征的过程上看,两种答案呈现出不尽相同的形成路径:小朱的原生态表征是通过观察,发现从第二个图形开始八边形就重合在一起了,2个八边形有1条边重合,3个八边形有2条边重合,以此类推n个八边形有n-1条边重合,n个八边形有8n条边,减去重合的n-1条边,那么就需要8n-(n-1)根小棒了;教师的精致化表征是将每个图形中的小棒个数写出来,然后发现1个八边形是8根,2个八边形是15根,3个八边形是22根,从小棒根数与八边形个数的数据内部关系中得出:小棒的根数是八边形个数的7倍多1,所以n个八边形需要7n+1根小棒。它们都具有其特定的思维视角,各自从不同的角度揭示和反映了两个数量之间的本质联系,应该说都具有独特的内在思维价值,而我们知道内在价值是“无价之宝”,无价之宝是无法进行比较的。从实际操作来看,精致化表征可以从数学情境中生成即直接建构,如老师向学生介绍的这种思路;也可以已有的原生态表征为依托,通过引入数学元素进行化简,形成更凝练的精致化表征即间接建构,如小朱所理解的由8n-(n-1)到7n+1的化简过程,这种间接建构既反映了二者之间的联系,同时也是对原生态表征的内在价值的充分肯定。
综上所述,像本例中教师这样“厚此薄彼”所作出的评判,视原生态表征为未完成品,而视精致化表征为成品,并将精致化表征视为唯一恰当的表征样式的认识无疑是错误的。
二、 横向数学化与纵向数学化何去何从
那么,在我们的教学实践中,如何恰当地处理这两种表征方式之间的关系才能更加有利于学生认知结构的完善,更加有利于学生思维的发展和数学能力的提升?笔者以为,将数量关系的原生态表征与精致化表征并重?并促进两者之间的互补与整合,无疑是数学教学明智的选择。为何要并重,如何互补与整合?弗赖登塔尔的数学化思想应该能给我们以一定的启示。
弗赖登塔尔认为:当我们把数学当成一种活动,它的一个主要特征是数学化。数学化可分为横向数学化与纵向数学化,横向数学化注重从生活到数学,从现实情境到数学体系,而纵向数学化注是数学体系内部的变换、重组。本例中,无论是原生态表征8n-(n-1),还是精致化表征7n+1,都可以直接从横向数学化的维度得到,即都可以对图形观察、分析,然后抽象出关系;与此同时,精致化表征7n+1还可以通过将原生态表征8n-(n-1)以化简的方式进行数学内部的重组即纵向数学化的维度得到。
从横向数学化和纵向数学化进行分类,数学教育可以分成四种类型:缺少横向数学化,也缺乏纵向数学化,是机械主义的教学;横向数学化得到成长,但纵向数学化不足,是经验主义的教学;横向数学化不足,但纵向数学化被培养起来,是结构主义的教学;横向数学化与纵向数学化都得到成长,是现实主义的教学。当下我国基础教育数学课程改革倡导现实主义的教学,横向数学化与纵向数学化要结伴而行、均衡发展。[1]
这样,就从数学化的角度为我们提供了理论依据:数量关系表征应该从单一的精致化转向以两者并重,这就要求教师在教学实践中必须重视学生的原生态表征,但又不能让学生的认知发展仅仅停滞在“自发”的水平上,要及时引导学生由原生态表征向精致化表征提升,并实现两者的互补与整合。所以,当学生得到原生态表征之后,教师可以通过引导学生转换思维方式从横向数学化的维度直接构建精致化的数量关系,也可以引导学生运用已学过的数学定律、性质对原生态的表征进行形式化处理,从纵向数学化的维度逻辑推理出精致化的数量关系。但就这种间接建构的方式而言,教师必须注意的是:尽管学生经历了由原生态向精致化的逻辑推理,但并不意味着学生随之自然而然地建立起与精致化相对应的数学思想方法,还存在知识与方法“分离”的危险。因此,对于形式化推演出来的精致化表征,教师应及时引导学生将其与数学概念、直观图形联系起来综合考查,使学生发现、领悟和建立起与精致化表征相对应的数学思想方法,实现思维方式的转换,建构起精致化数量关系表征的完整意义。[2]
就本例而言,教师在评讲试题时,一方面要充分肯定学生给出的这个答案,并鼓励学生将这种答案及其思考过程向全体同学展示;另一方面,也要引导学生将这个答案进一步化简为7n+1,使之在形式上更加简洁以体现数学的特征。更重要的是引导全体学生从题中的图形出发,从不同的思维视角建构起7n+1的实际意义。
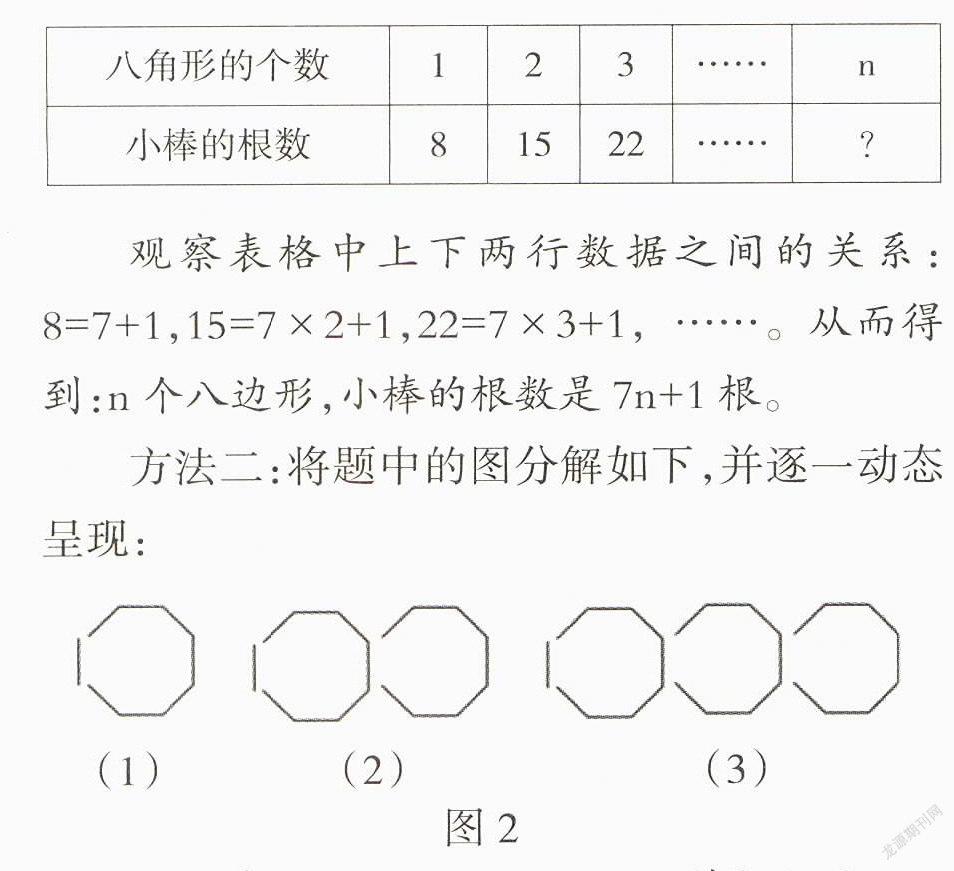
方法一:根据题中的图形,形成下列表格:
观察表格中上下两行数据之间的关系:8=7+1,15=7×2+1,22=7×3+1,……。从而得到:n个八边形,小棒的根数是7n+1根。
方法二:将题中的图分解如下,并逐一动态呈现:
引导学生发现:1个八边形,小棒根数是1+7根,2个八边形,小棒根数是1+7×2根,3个八边形,小棒根数是1+7×3根,……。从而得到:n个八边形,小棒的根数是1+7n根。
从更高的层次来看,坚持数量关系原生态表征与精致化表征并重、横向数学化与纵向数学化结合,不仅仅是为了学生认知结构的完善,更重要的是为了学生智慧的生成与发展。学生可以从多种角度去思考问题,其思维视角是多向的,其思维方式是多样的。如此的数学教学才能真正“使人具有活跃的智慧”,数学学习才能真正成为“智慧之学”。
参考文献
[1] 王永.寻找均衡的数学化[J].人民教育,2006(1).
[2] 张彪.数量关系表征:原生态与精致化的辩证思考[J].福建教育(小学版),2007(12).
【责任编辑:陈国庆】

