回归分析法在水位预测中的应用

王盼秋，曾　丹，孟凡宇

（1.淄博市水文局，山东 淄博 255000；2.临沂市水文局，山东 临沂 276000）

回归分析法在水位预测中的应用

王盼秋1，曾丹2，孟凡宇1

（1.淄博市水文局，山东 淄博 255000；2.临沂市水文局，山东 临沂 276000）

【摘要】通过对大武水源地1986—2011年枯水期水位、开采量、降水量等多个长系列实测资料的统计分析，建立了多元线性回归模型，对模型进行F检验和T检验修正后，利用该模型进行水源地次年枯水期水位预测。结果为实测资料与模拟预测值的误差在5%以内，表明该方法预测精度较高，适用于该水源地水位预测。

【关键词】大武水源地；线性回归；水位预测

地下水动态的分析，尤其是地下水源地水位的精确预报及趋势分析，对水源地的管理和开采布局的适时调控起着至关重要的作用，有利于水资源的可持续利用。另外，对防止地面沉降、地下水污染等地质环境灾害有着积极作用。本文以淄博市大武水源地为例，选用多元线性回归模型，对其枯水期水位进行了分析预测，旨在为水源地的合理调控提供依据。

1　大武水源地概况

大武水源地位于山东省淄博市临淄区境内，指位于临淄区的大武、辛店、南仇3个地下水源地的闭合富水区域，总面积110km2，可开采资源量40万m3/d。

大武水源地开采程度一直较高，供水范围涉及城市生活、工业、农业灌溉等各个方面。从大武水源地历年开采量可知，大致可分4个阶段：开采量大幅度上升期（1980—1996年），开采量缓慢减少期 （1996—2001年），开采量大幅度压减期（2002—2011年），保护性开采期 （2011-07以后）。经统计，1980—2012年大武水源地多年平均开采量14718.3万m3，其中2002年以来年平均开采量11925万m3。

从大武水源地历年地下水位曲线可知，自1980年以来，受高强度开采和降水丰枯变化等影响，大武水源地水位经历了1980—1990年、1991—1996年、1997—2005年3个升降周期，表现为下降（持续或稳步或间断）～回升（急剧或连续）状态。2006—2010年为相对稳定阶段，水源地总体上采补平衡，地下水位变化较平稳，水位一般保持在25～35m。根据1980年运行以来水位动态资料可知，其有以下变化特征：1）地下水位年际变幅大，季节性变化明显。2）各富水段表现出平盘升降的特征，表明富水地段之间存在着密切的水力联系。

2　模型建立与求解

2.1多元线性回归模型介绍

回归分析法是指在掌握了一定量的观测数据的前提下，用数理统计的方法建立变量与自变量之间的回归函数关系。回归分析根据自变量个数的多少可分为一元回归分析和多元回归分析。按照回归表达式的形式又可分为线性回归分析和非线性回归分析。多元线性回归模型就属于回归分析的一种，该方法多用于水文地质条件复杂的地区。

多元线性回归模型的因变量与自变量之间为线性关系，数学模型为：

Y=b0+b1X1+b2X2+……+bpXp+e

其中：Y为因变量，Xi（i=1，2，3，……，p）为自变量，b0，b1，b2，……，bp为未知回归参数，e为随机变量。

对于一组数据（X1，X2，……，Xp，Y），回归模型由两部分组成，即b0+b1X1+b2X2+……+bpXp和e，即观测因素和非观测因素。当随机误差e的平方和最小时，回归方程的拟合程度就最好,基于这种思想求未知参数b0，b1，b2，……，bp的方法叫最小二乘法。

用最小二乘法求得模型参数的估计值后,还需要进行显著性检验。常采用两种方式进行检验，一是对回归参数的显著性检验（T检验），用于检验每个变量Xi对因变量Y影响的显著性；二是回归方程的整体线性显著性检验 （F检验）,用于检验Y与变量Xi之间的线性关系是否显著。

2.2回归模型建立与求解

对水源地1980—2012年因变量Y（次年6 月1日水位）和自变量Xi（当年10月1日水位、当年10.1至次年6.1降水量、当年汛期降水量、时段开采量、黑旺铁矿排水量、当年10月至次年5月补源量、当年7~9月补源量）进行统计，如表1示。通过Matlab对数据进处理计算，用最小二乘法得到模型的回归参数bp见表2和方差分析见表3。

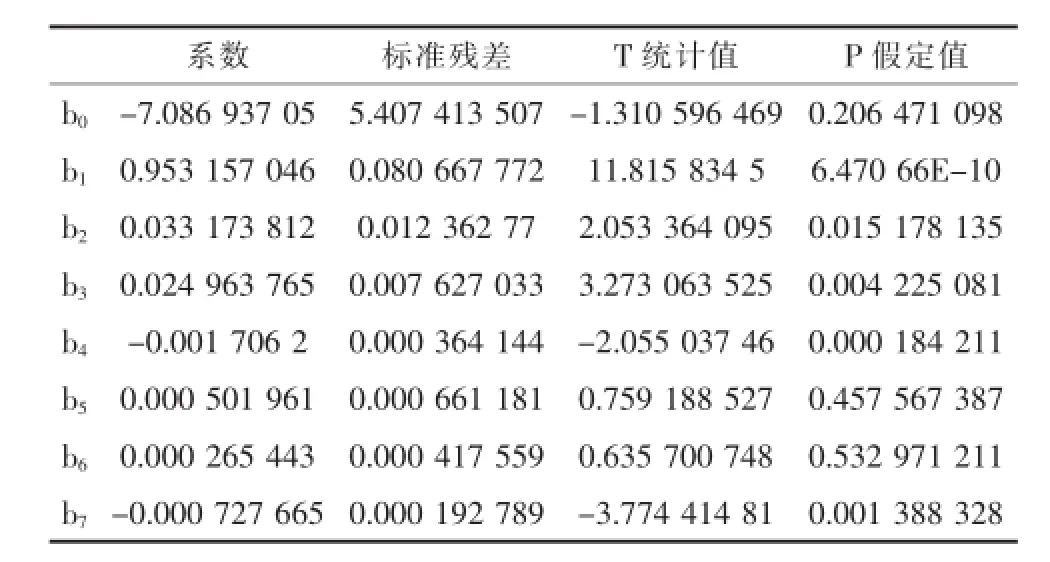
表2　回归方程参数表

由表2得出回归方程为：

Y=-7.087+0.953X1+0.033X2+0.025X3

表3　方差分析表

-0.002X4+0.0005X5+0.0003X6-0.0007X7

在显著性水平为0.05的情况下对方程进行F统计检验，由表3知该方程的F值为76.11，故：

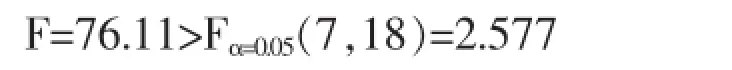
证明该回归方程显著。

在显著性水平为0.05的情况下对各自变量参数进行T检验，查T值表得：

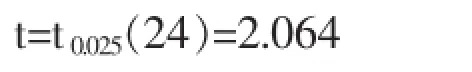
当表2中各参数对应T值的绝对值小于2.064时，即|Ti|＜2.064时自变量对因变量Y有显著性影响。统计结果表明，只有10月1日至次年6月1日降水量、10月1日至次年6月1日开采量、黑旺排水量、10月1日至次年6月1日补源量对水源地次年枯水期水位即6月1日水位有着显著性影响，其他因子对次年6月1日水位的影响显著性稍差。

3　精度检验

利用多元线性回归模型计算得大武水源地1986—2001年次年6月1日水位预测值，并求得预测值的绝对误差和相对误差。从对比情况可见，除极个别年份外预测值绝对误差较小，相对误差在10%以内，对实测水位与预测水位进行曲线拟合，两曲线拟合程度较好，预测结果与实测数据较为符合。

4　结语

1）采用多元线性回归模型，对大武水源地次年枯水期水位进行超前预测，结果表明，预测精度较高，方法可以采用。

2）由结果可知，模型预测值与实测值误差较大的点为序列的极值点，这是吉布斯现象的反应。

3）在预测的过程中，应根据序列的加长和结果的误差精度，对参数值进行合适的调整。同时随着自变量等因素的变化，应不断检验参数影响的显著性，选取不同自变量组合并改变回归方程进行预测。

4）利用多元线性回归模型对水源地次年枯水期水位进行超前预测，对于水源地开采模式及开采量的合理调整，提高供水保证率，水资源的可持续利用等方面均可起到至关重要的作用。

（责任编辑 崔春梅）

【中图分类号】P641.7

【文献标识码】B

【文章编号】1009-6159（2015）-03-0029-03

收稿日期：2014-12-11

作者简介：王盼秋（1987—），男，助理工程师