填方渠堤沉降变形拟合及预测分析

李廷高，赵含雨，张　峰

（1.山东黄河东平湖工程局，山东 泰安 271000；2.山东黄河河务局东平湖管理局，山东 泰安271000）

填方渠堤沉降变形拟合及预测分析

李廷高1，赵含雨2，张峰1

（1.山东黄河东平湖工程局，山东 泰安 271000；2.山东黄河河务局东平湖管理局，山东 泰安271000）

【摘要】根据南水北调安阳段工程渠堤沉降变形资料，用双曲线预测公式对其进行分析，得到了预测公式的各个系数。由于该预测公式的局限性，提出了一种包含堤高的沉降变形预测公式，并对类似工程的沉降变形进行了拟合和预测。

【关键词】南水北调；填方渠堤；沉降变形；拟合

填方渠堤的沉降由瞬时沉降、固结沉降（也称主固结沉降）和次固结沉降3部分组成，由于实际填筑土体与设计和试验的差异性，理论计算的沉降往往与实际值有较大的差异。大量的工程实践表明，要准确地计算填筑渠堤的沉降，特别是预测填筑施工完成后沉降，仍是一个需要解决的关键问题。工程实践中，可利用施工前期观测得到的沉降资料，找出沉降规律，利用有限时间内的沉降观测资料预测沉降的发展趋势并推测未来沉降规律和总沉降量。常用的观测曲线拟合方法有三点法、指数曲线法、时间对数法、双曲线法和修正双曲线法等。河海大学许永明等提出一种抛物线形的时间对数法方程来确定最终沉降量的方法，其公式为s=a（lgt）2+blgt+c，式中参数a、b、c可用优化方法求得。

1　沉降监测资料分析

笔者收集了南水北调安阳段4个渠堤断面的变形监测资料，各断面基本情况见表1。

表1　安阳段部分填筑渠道施工情况

原始观测点如图1、图2所示，由于全部为填筑至渠顶后沉降，所以各组数据可以采用双曲线模拟。但需要说明的是，监测起始时间与填筑至渠顶的时间不一致，监测起始时间较为滞后。

图1　A1和A2两个断面沉降变形过程线

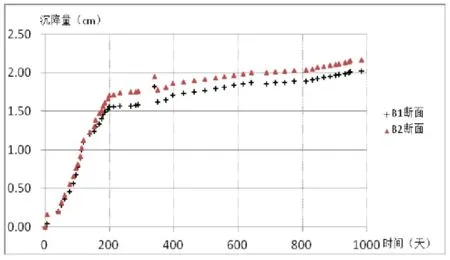
图2　B1和B2两个断面沉降变形过程线

因监测初期的沉降变形值有一定波动，拟合时考虑局部数据的这种特性，进行分段模拟。从图形上看，整体数据按沉降速率的快慢设置分界线为t=200d比较合适，200d以内沉降速率有所波动，但平均沉降速率较大，200d以后沉降速率明显变缓。为使拟合曲线更符合实际，前段用高次幂方程曲线拟合，后段采用双曲线进行模拟。

1.1函数拟合

1）分段函数模拟，经多次试算，拟采用三次曲线和双曲线结合的分段函数，方程为：

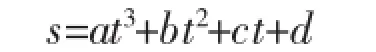
2）双曲线方程为：

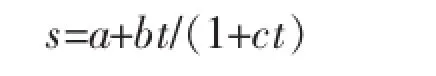
式中：t为基准期后的天数，d；s 为沉降量，cm。

A1（A1－1为测点1，A1－2为测点2，下同）和A2断面数据整理结果及曲线拟合相关参数见表2。

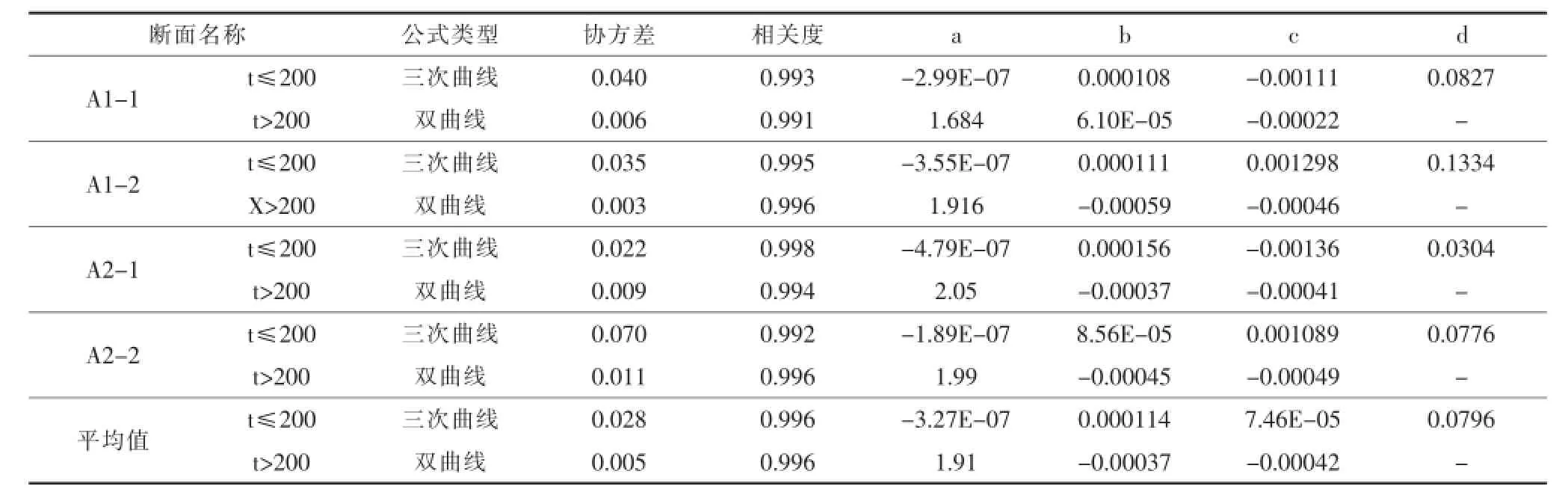
表2　参数及拟合度表

A1和A2监测数据最终拟合的曲线方程为：

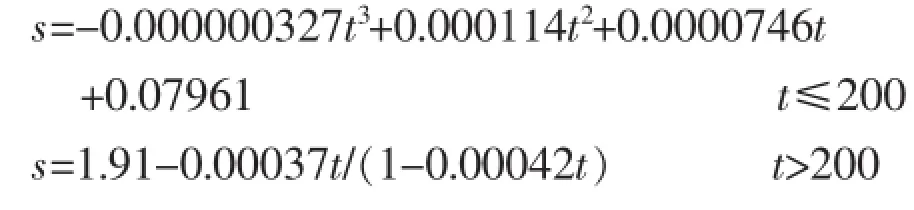
B1和B2监测数据最终拟合的曲线方程为：

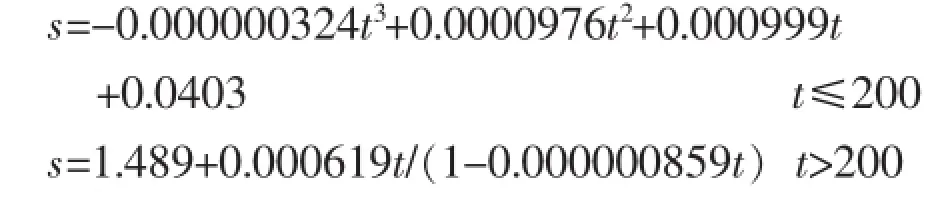
1.2整体函数模拟

采用上述方程虽能模拟填方渠堤沉降变形，但具有一定的局限性，表现在两方面，一是未能反映渠堤填筑完成时刻至监测起始时间内发生的沉降量；二是未能反映与渠堤填筑高度的关系。对填筑材料压实特性、地下水情况等暂不考虑。

为此，笔者对上述方程进行改进，改进公式为：

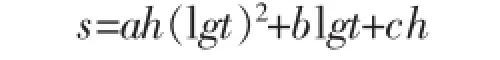
式中：参数a，b，c用优化方法求得；s为最终沉降量，cm；t为填筑至渠顶后的监测时间，d；h为渠堤填筑高度，m。

根据估计的数据系列，用上述改进抛物线公式进行拟合，拟合后的公式为：

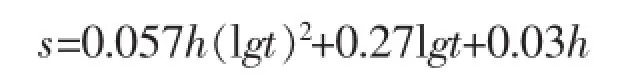
2　施工期沉降量预测应用

采用上述公式对温县段未填筑的缺口渠堤进行沉降计算，其中，根据已有的工程经验，按该式预测计算时，90d以前的不采用上述公式预测，最终沉降量按720d的沉降量进行估算。计算成果见表3。

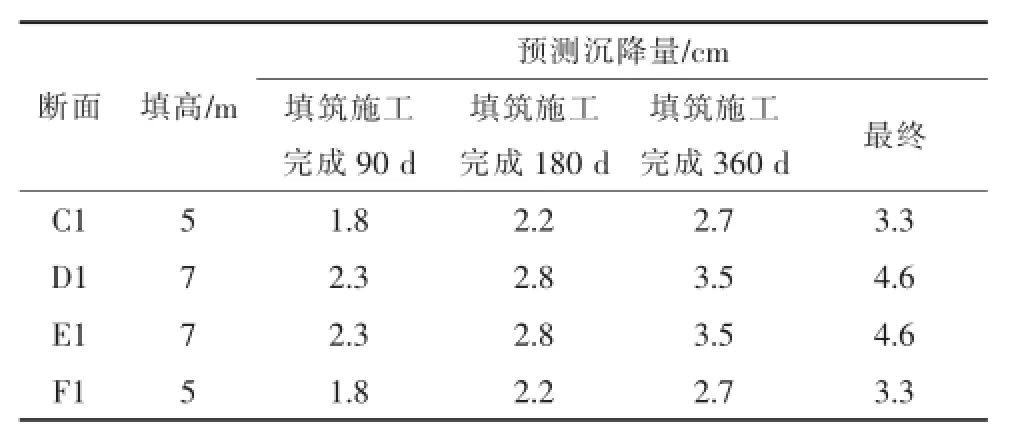
表3　温县段渠道未填筑缺口渠段沉降量预测

从表3可以看出，对于7m高的填筑渠道，预留5cm的沉降超高比较合适，对于5m高的填筑渠道，预留3.5cm的沉降超高比较合适。

3　结语

1）渠堤在填筑施工完成后，均将产生一定量的沉降变形。2）对于一般黏性填土，渠顶沉降变形一般在3年内基本完成，初期6～10个月约完成总沉降量的80%。3）对已有的安全监测资料进行整理分析，预测类似渠堤沉降变形，为预留沉降超高等具有重要意义。

（责任编辑 崔春梅）

【中图分类号】TV672

【文献标识码】B

【文章编号】1009-6159（2015）-03-0034-02

收稿日期：2014-11-12

作者简介：李廷高（1969—），男，高级工程师