基于后置带通滤波的中频信号A／D变换精度提高方法＊

陈 媛 马曼丽 殷勤业

（西安交通大学电子与信息工程学院，西安，710049）

引 言

模／数转换技术作为跨接连续模拟量和离散数字量的桥梁，广泛应用在数字通信、数字测量、多媒体等技术领域。数字技术的不断发展对模／数转换器的性能提出了更高的要求。模／数转换器的主要性能指标包括有效变换位数（分辨率／精度）和最高采样速率，一般来说，高精度模／数转换器只适用于频率不高的信号，而适用于高频信号的高速模／数转换器的精度又不会很高。目前，有两种常用的方法来提高模／数变换器的分辨率：一种见于Σ-Δ型模／数转换器，依靠过采样，把信号基带以内的噪声推到高频处，然后经过低通滤波把高频噪声滤除。然而，这种增量调制型模／数转换器实际上是以速度换取精度，过采样率通常是信号最高频率的几十甚至上百倍，因此，这种方法仅在低频场合得到了广泛应用［1-4］。此外，这种增量调制法还会存在误差累积的问题。另一种提高模／数变换器分辨率的方法是通过增加比较器的数目，然而，这样会增加芯片面积和制造的复杂度［5-6］。

移动通信的迅速发展，对无线接收机提出了严格的要求，目前，绝大多数的无线接收机的前端采用超外差式，把宽频段的射频信号转变为中频信号，以获得高Q值和高中频增益（这比将频率搬移到零中频所获得的增益高很多），再对中频信号直接采样，以进行数字信号处理［7-8］。这其中就涉及到模／数转换过程，其产生的量化噪声（也称量化误差）是衡量模数转换器分辨率的关键指标。由于中频频率较高，这样对模／数转换器的性能就提出了很高的要求。本文采用的是后置的数字带通滤波器，并且要以此滤除A／D转换过程中产生的量化噪声，而目前大部分中频接收机采用的是用来抗混叠的模拟带通滤波器，是针对采样前的信号使用的，该模拟滤波器对A／D量化之后才产生的量化噪声的消除没有任何效果。此外，在较高频率范围内，由于受到工艺条件、设计等方面的限制，国内直接制造高精度模／数转换器的技术与国外存在明显差距，这对我国的国防现代化和民用电子工业的发展非常不利。如何在现有资源和技术条件下提高模／数转换器的精度是很有意义的。因此，本文将着重于研究通过后置数字带通滤波减小中频带通信号A／D量化噪声，应用低位模／数转换器和后置滤波器相结合的办法，来提高模／数转换器的精度。这在目前国内高性能模／数转换器制造技术不高，资源受限，主要依靠进口的条件下，不失为一种行之有效的方法。应该指出的是，这种方法需要针对不同信号的带宽设计相应的后置数字带通滤波器。对于A／D生产商来讲，可能会应用受限，然而对于特定的通信环境，还是有其应用价值的。

1 量化噪声的理论模型分析与处理

模拟信号xa（t）经采样和理想A／D量化，成为离散时间信号x（n），其结果准确地代表采样值；再对x（n）量化，使字长固定在b位，产生的信号用（n）表示，则量化误差为对于定点制补码舍入误差，由于其正负对称性，它总是在-q／2和q／2之间。其中，q＝2-b，称为量化阶［9-10］。

1.1 量化效应的理论模型分析

对信号序列x（n），设量化误差序列e（n）是一个与其不相关的加性噪声序列。一个实际的A／D变换可看作一个理想A／D变换在输出端加入一个噪声序列e（n）［11］，其模型如图1所示。

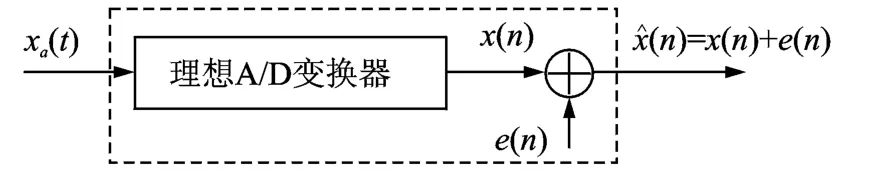
图1 A／D变换的分析模型Fig.1 Analytical model of A／D conversion

被广泛接受的统计学观点认为［12-14］，对大多数不规则的信号来说，图1模型中的e（n）是加性白噪声序列。而本文在模型分析中并不强调e（n）一定要是白噪声序列。事实上，白噪声这一假设对于本文提出的后置带通滤波法提高A／D转换器精度来说，并不是必要的，关键是要看相应的量化噪声谱是否在滤波器的通带范围内，2.3节将以一个简单的单频正弦信号为例来详细说明和证实这一理论。

根据维纳-辛钦定理

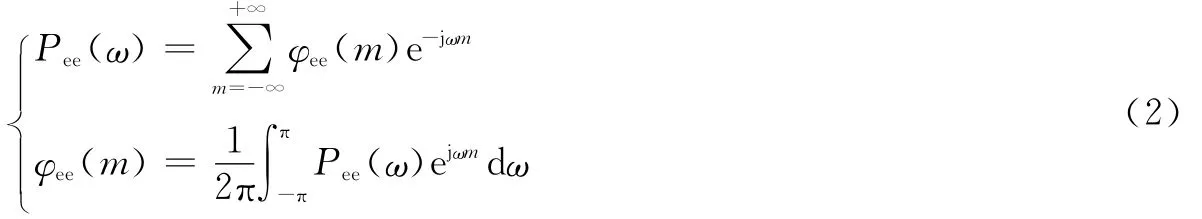
得到量化噪声的总功率

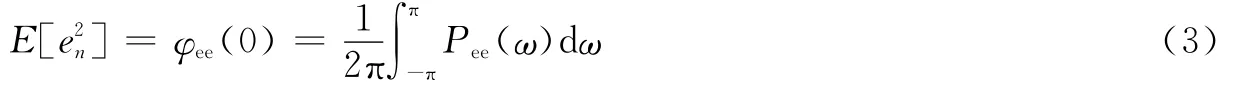
其中，Pee（ω）为e（n）的功率谱密度，φee（m）为自相关函数。

1.2 量化噪声通过线性系统的响应

量化噪声通过线性系统的框图如图2所示，根据线性系统的齐次性和叠加性，可知加性的输入噪声在系统的输出端仍为加性。

图2 量化噪声通过线性系统Fig.2 Quantization noise getting through linear system

量化噪声e（n）通过一个LTI系统H（ejω）后，系统的输出噪声可表示为ef（n）＝e（n）＊h（n）。

功率谱密度变为

所以，通过线性系统后量化噪声的功率为

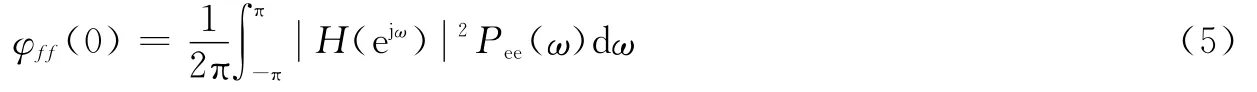
当H（ejω）是理想带通滤波器时，设截止频率分别为ωa和ωb（考虑到信号非理想带限，ωa和ωb的选择应使信号完全在滤波器通带内，并使通带尽可能的窄），则

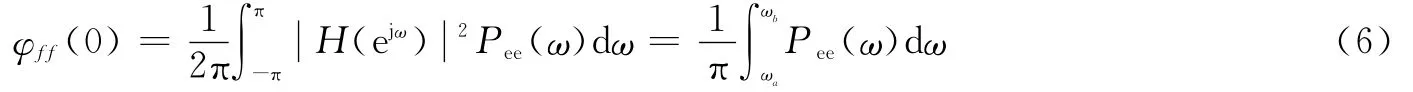
通过上式看出，加入一个不损伤信号的带通滤波器后，量化噪声的减小关键要看相应的量化噪声谱是否在滤波器的通带范围内：落在通带外的量化噪声分量越多，滤波后噪声功率减小的越多，带通滤波的效果就越好；反之，落在通带内的量化噪声分量越多，带通滤波法的效果越不明显。

2 后置带通滤波法对A／D变换性能的改善

目前，采样速率在500MHz以下的8位A／D芯片较为通用，市场售价便宜，性价比高；而高性能的A／D芯片不仅制造技术复杂，价格也相对昂贵。因此，希望能够通过信号处理的方法，以8位A／D芯片为例，用低位A／D芯片获得更高位A／D芯片的量化精度。按统计方法，量化噪声为白噪声序列时的方差可表示为＝q2／12，这样，对于一个8位A／D变换器，量化噪声方差为：而对于一个10位A／D变换器＝7.947×10-8，可见，10位A／D变换器的量化噪声方差比8位的小两个数量级。此外，量化噪声方差与A／D变换的有效位数直接相关：位数越高，q越小，量化噪声方差也就越小，而方差又是功率的表现，因此，要想在不改变A／D芯片的情况下提高A／D变换的精度，可以从减小量化噪声的功率着手。

2.1 通用的中频采样与A／D变换量化系统

加入后置数字带通滤波器后的通用中频采样与A／D变换系统如图3所示。首先，原始模拟信号x（t）通过一个抗混迭滤波器ha（t），变为带通信号xa（t），作为整个A／D变换系统的输入信号，xa（t）是一个带通的中频信号，其频谱如图4所示。然后，对xa（t）进行采样、量化，得到数字信号（n）；最后，加入带通滤波器hd（t）对e（n）进行滤波处理来减小量化噪声，而这种滤波不应伤及信号x（n）。根据式（6），落在通带外的噪声分量越多，滤波法减小量化噪声的效果就越显著。

图3 通用中频采样与A／D变换量化系统Fig.3 Sampling in medium frequency and A／D conversion

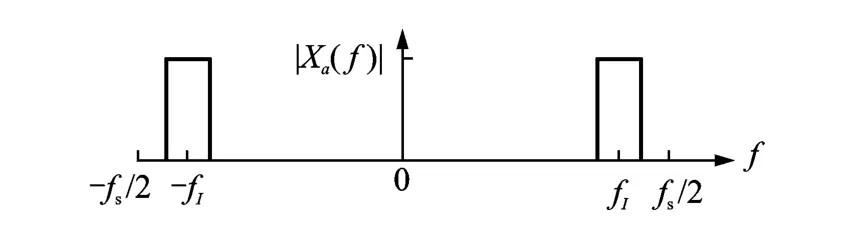
图4 中频信号频谱及采样速率示意图Fig.4 Schematic diagram of IF bandpass signals spectrum and sampling rate

2.2 后置带通滤波法改进A／D量化性能

以实际中常用的中心频率fI＝70MHz的中频信号为例，由于抗混迭滤波器ha（t）是模拟滤波器，不能通过计算机仿真实现，因此需要直接生成一个带通的模拟信号xa（t），图5，6涉及的仿真中，xa（t）由7个不同频率的单频正弦信号叠加而成，落在65～75MHz频带内，带宽近似为10MHz。

为满足奈奎斯特定理，以频率fs＝1／T＝160MHz对xa（t）采样，生成采样序列xa（nT），再进行8位A／D量化（以此来模拟8位A／D变换器的精度）得到量化后的信号为（n）。用（n）与xa（nT）相减得到量化噪声序列e（n），并且做出其功率谱图。然后，加入用频率采样法设计的第二类线性相位FIR带通滤波器，阶数为56，上下截止频率分别为65MHz和75MHz，对量化噪声进行滤波处理，由于信号完全在滤波器通带内，因此滤波过程不会伤及信号。

经过带通滤波器前后，量化噪声的功率谱如图5所示，结果表明：带外的量化噪声被滤除，只剩下通带内的量化噪声。

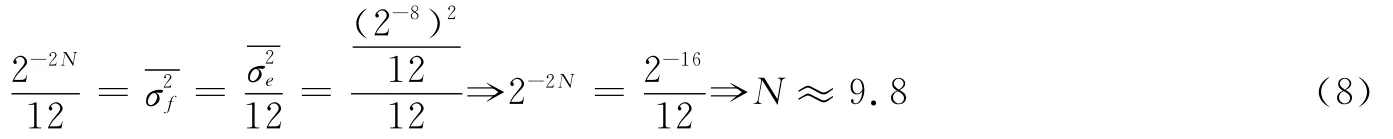
N＝9.8意味着在没有更换A／D芯片，也没有改变采样速率的条件下，通过增加后置带通滤波器，用8位A／D芯片达到了相当于9.8位A／D芯片的性能。提高采样速率为320MHz时，量化噪声如图6。仿真数据结果见表2。

图5 量化噪声通过滤波器前后的功率谱Fig.5 The power spectrums of quantization noise before filtering and after filtering

表1 滤波前后量化噪声的均值和功率Table 1 Means and powers of quantization noise before and after filtering

表2 提高采样率时滤波前后量化噪声的均值和功率Table 2Means and powers of quantization noise before and after filtering when increasing sampling rate

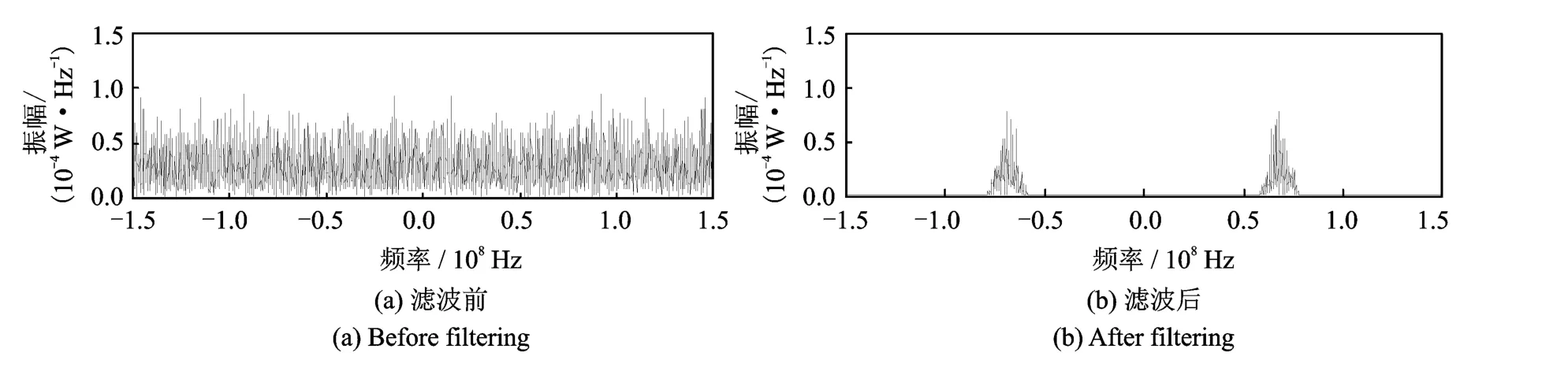
图6 采样频率为320MHz时，量化噪声通过滤波器前后的功率谱Fig.6 Power spectrums of quantization noise before filtering and after filtering when sampling rate is 320 MHz

由表2可见，经过带通滤波器滤波后的量化噪声减小为原来的1／20。类似地，在没有更换A／D芯片，提高采样速率的条件下，结合后置带通滤波器，用8位A／D芯片达到了相当于10.2位A／D芯片的性能。需要说明的是，仿真中没有考虑实际中可能存在于通带内的热噪声等背景噪声，由于通带内背景噪声的功率不会随采样频率的提高而减小，所以，即使采样率无限提高，改善后的A／D精度也不能无限提高。

改变中频信号的带宽为近似16MHz，此时的后置数字带通滤波器的截止频率变为62MHz和78 MHz，阶数仍为56阶，采样频率160MHz。则经过滤波器前后量化噪声的均值和功率见表3。

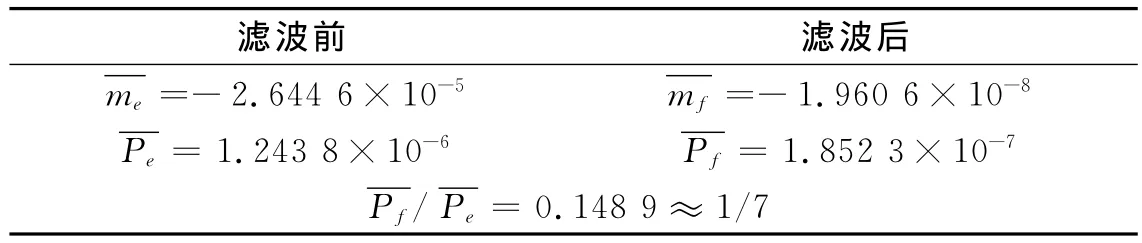
表3 改变信号带宽滤波前后量化噪声的均值和功率Table 3 Means and powers of quantization noise before and after filtering when changing signal bandwidth

此时，经过带通滤波器滤波之后的量化噪声功率减小为原来的1／7，计算可得，经过后置带通滤波器后，8位A／D芯片达到了相当于9.4位A／D芯片的性能。对比表1所示的10MHz信号带宽时的情况，A／D芯片精度的改善程度有所下降。这是因为，信号带宽增加，相应的滤波器通带带宽也增加，落入通带内的量化噪声增多，经过滤波器后滤除的带外噪声减小。然而，相对于原来的8位，A／D芯片的精度还是有了显著提高。

总结输入模拟信号为多个单频正弦信号叠加时的情况，各频率分量的选择使得信号在仿真时间内是非周期的，且量化噪声不呈现周期性；此外，由于量化舍入处理是非线性的，因而量化噪声的功率谱会弥散在整个频域范围内，这样，带通滤波器就可以滤除带外噪声，使噪声功率大大减小。

考虑到数字滤波器多是用FPGA分布式算法实现的，而直接实现高精度A／D变换器的技术复杂度远大于加入数字滤波器的复杂度，因此，通过数字滤波器使低位A／D转换达到高位A／D转换性能而获得的收益是大于其代价的，表明滤波法改善A／D性能很有实际意义。

2.3 对传统理论模型的改进分析和说明

传统的统计学观点将量化噪声当作白噪声处理，然而，这种统计假设并不一定符合实际情况，实际中的量化噪声形式多样，并不一定为白噪声，这时，就不能应用白噪声的假设模型。本文提出的后置带通滤波法对量化噪声的多种情况都适用，没有白噪声假设条件的限制。下面通过几种量化噪声的典型情况来进行后置带通滤波法改善A／D变换精度的性能分析。

以xa（t）为规则的单频正弦信号为例，频率选择仍为中频信号频率70MHz，采样频率为210MHz，恰好是信号频率的整数倍，采样信号和量化噪声的功率谱如图7所示。由图7可知，该信号量化噪声的功率谱是线谱，仅在70MHz处有一个频率分量，即量化噪声谱与信号谱完全重合。然而，若采样频率不是信号频率的整数倍，量化噪声功率谱就可能表现出不同的形式。图8即为信号频率70MHz，采样频率210.3MHz时，采样信号与量化噪声的功率谱。由此看出，其量化噪声有近似白噪声的谱特性。继续改变采样频率为212MHz，采样信号与量化噪声的功率谱如图9所示，此时，量化噪声的功率谱为一系列线谱的组合，并且它在信号频率（70MHz）附近的分量较少。进而，考虑以上3种情况在后置带通滤波法中的适用情况。重复2.2节所述的步骤，分别将3种不同采样频率下的量化噪声通过带通滤波器，滤波后A／D精度改善程度对比如表4所示。

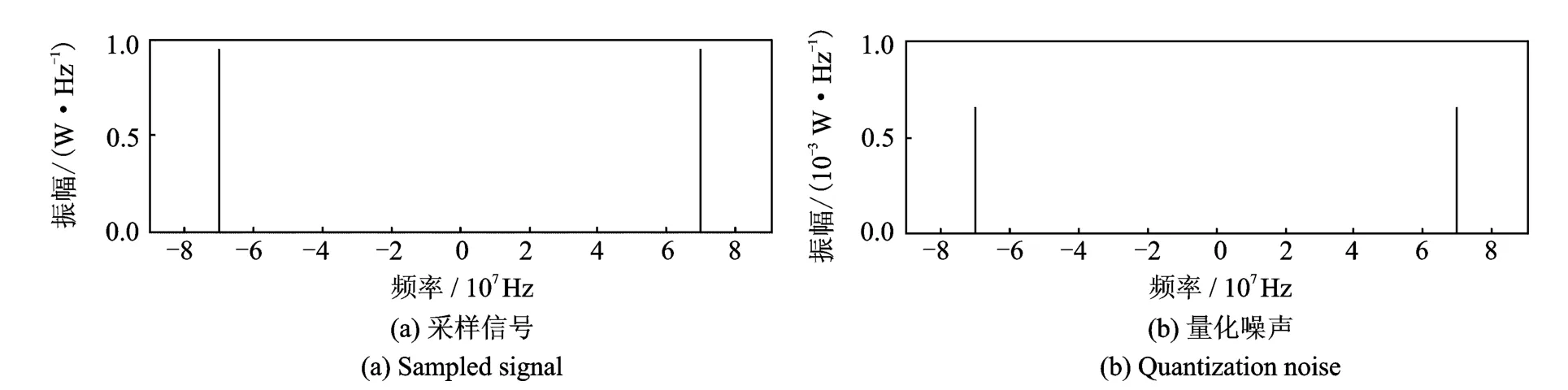
图7 当xa（t）＝sin（2π·70·t），fs＝210MHz时，采样信号与量化噪声的功率谱Fig.7 Power spectrums of sampled signal and quantization noise when xa（t）＝sin（2π·70·t），fs＝210MHz

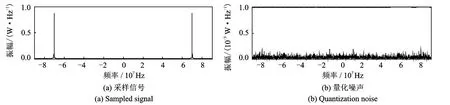
图8 当xa（t）＝sin（2π·70·t），fs＝210.3MHz时，采样信号与量化噪声的功率谱Fig.8 Power spectrums of sampled signal and quantization noise when xa（t）＝sin（2π·70·t），fs ＝210.3MHz

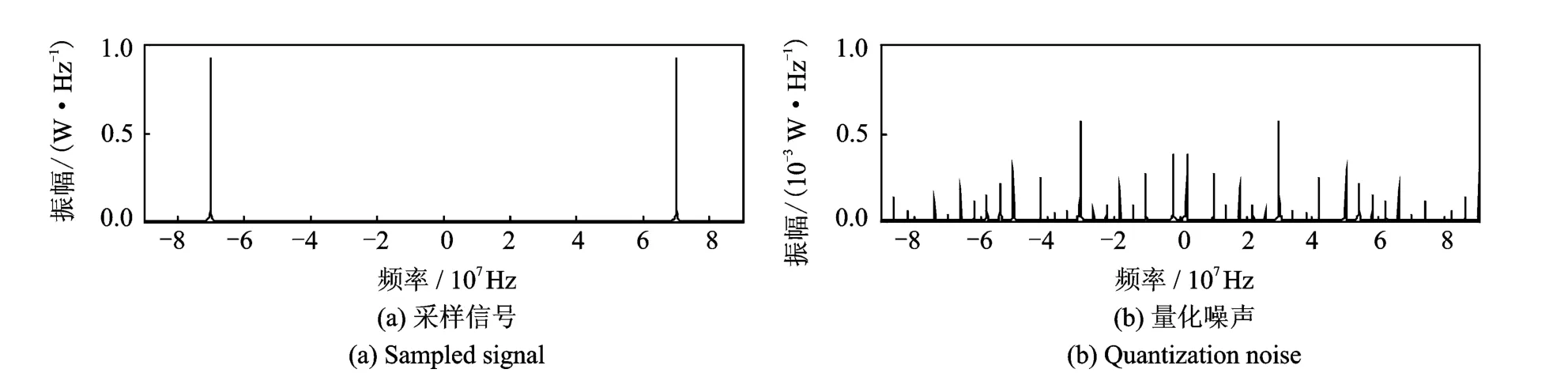
图9 当xa（t）＝sin（2π·70·t），fs＝212MHz时，采样信号与量化噪声的功率谱Fig.9 Power spectrums of sampled signal and quantization noise when xa（t）＝sin（2π·70·t），fs ＝212MHz

表4 不同采样频率下滤波后A／D精度改善程度对比Table 4 Comparison of A／D resolution improvement under different sampling frequencies after filtering

从表4的数据可以看出：采样频率恰好是信号频率的整数倍时，由于量化噪声功率谱与信号谱完全重合了，并且都在带通滤波器的通带范围内，没有弥散到带外，此时，滤波后量化噪声的功率基本不变，这种情况下，整个A／D量化系统的性能不会通过滤波法得到改善。而对于另外两种情况，滤波后量化噪声的功率比滤波前都有显著地减小，A／D变换的位数也得到了显著提高。在实际应用中，由于采样频率很难精确到恰好是信号频率的整数倍，对比前两种情况可以看到，即使是微小的采样频率偏差（0.14%的偏差）也会导致噪声谱的扩散，因此，在实际中出现的往往是后两种情况，而非第一种情况。此外，值得注意的是，采样频率为212MHz时，量化噪声的功率谱为线谱叠加，非白噪声谱，且在信号频率（70MHz）附近的分量较少；从滤波效果上看，此时量化噪声功率的减小以及A／D变换位数的改善程度比白噪声时的效果好很多，这就说明了后置带通滤波法适用范围更广，并不局限于量化噪声为白噪声的条件。

量化噪声的谱特性是模拟信号频率和采样频率综合作用的结果；在后置带通滤波法中，量化噪声并不要求一定是白噪声，关键要看相应的量化噪声谱是否在滤波器的通带范围内：落在通带内的量化噪声比例越小，后置带通滤波法改善A／D变换性能的效果越好，甚至可能好于量化噪声为白噪声时的情况；而落在通带内的量化噪声比例越大，后置带通滤波法的效果越不明显。

3 结束语

本文提出了后置带通滤波法减小中频带通信号经A／D转换带来的量化噪声，从而提高A／D转换器精度的方法，该方法采用后置的数字带通滤波器滤除带通信号在A／D转换过程中产生的带外量化噪声。仿真结果表明，以满足奈奎斯特率的采样频率，对经由A／D转换后的带通信号进行带通滤波处理，就可以令量化噪声大大降低，使低位A／D转换达到高位A／D转换的性能。这在目前高精度、高速A／D转换芯片价格高且资源稀少的市场情况下，为提高A／D转换精度提供了一个有效且相对低成本、易实现的方法。此外，本文还打破了传统模型中量化噪声为白噪声的条件限制，证明了后置带通滤波法不只局限于量化噪声为白噪声的情况，如果落在通带外的量化噪声更多，则带通滤波法改善A／D变换性能的效果会更明显。

［1］ 周化雨，张勤.带余弦预滤波和补偿滤波的抽取滤波器［J］.数据采集与处理，2008，23（z1）：145-151.

Zhou Huayu，Zhang Qin.Decimation filter with cosine prefiltering and compensation filtering［J］.Journal of Data Acquisition and Processing，2008，23（z1）：145-151.

［2］ Ebrahimi M M，Helaoui M，Ghannouchi F M.Delta-Sigma-based transmitters：Advantages and disadvantages［J］.Microwave Magazine，IEEE，2013，14（1）：68-78.

［3］ 李君.基于过采样技术提高 ADC分辨率探析［J］.现代电子技术，2010，33（6）：160-162.

Li Jun.Improving the resolution of ADC based on over-sampling［J］.Modern Electronics Technique，2010，33（6）：160-162.

［4］ Ebrahimi M M，Helaoui M. Reducing quantization noise to boost efficiency and signal bandwidth in Delta-Sigma-based transmitters［J］.Microwave Theory and Techniques，IEEE Transactions on，2013，61（12）：4245-4251.

［5］ Yefim S P.A new approach to increasing sensitivity and resolution of A／Ds［C］∥Aerospace Conference，2009IEEE.Big Sky，MT：IEEE，2009：1-15.

［6］ 王江安，庄奕琪，周清军，等.基于数字后处理算法的并行交替采样ADC系统［J］.数据采集与处理，2010，25（4）：537-542.

Wang Jiangan，Zhuang Yiqi，Zhou Qingjun，et al.8-bit 4-Gsps time-interleaved ADC based on digital post-processing calibration［J］.Journal of Data Acquisition and Processing，2010，25（4）：537-542.

［7］ Mirzaei A，Darabi H，Murphy D.A low-power process-scalable super-Heterodyne receiver with integrated high-Q filters［J］.Solid-State Circuits，IEEE Journal of，2011，46（12）：2920-2932.

［8］ 李天昀，许漫坤，葛临东.取邻抽取任意倍数采样率变换算法［J］.数据采集与处理，2012，27（2）：254-258.

Li Tianyun，Xu Mankun，Ge Lindong.Conversion algorithm between arbitrary sampling rate based on neighbor decimation［J］.Journal of Data Acquisition and Processing，2012，27（2）：254-258.

［9］ Naud J C，Menard D，Caffarena G，et al.A discrete model for correlation between quantization noises［J］.Circuits and Systems II：Express Briefs，IEEE Transactions on，2012，59（11）：800-804.

［10］黄翔东，王兆华.全相位FFT相位测量法的抗噪性能［J］.数据采集与处理，2011，26（3）：286-291.

Huang Xiangdong，Wang Zhaohua.Anti-noise performance of all-phase FFT phase measuring method［J］.Journal of Data Acquisition and Processing，2011，26（3）：286-291.

［11］Kabal P.Correlation properties of quantization noise［C］∥ Acoustics，Speech and Signal Pro-cessing（ICASSP），2011IEEE International Conference on.Prague：IEEE，2011：5244-5247.

［12］Gustavsson U，Eriksson T，Nemati H M，et al.An RF carrier bursting system using partial quantization noise cancellation［J］.Circuits and Systems I：Regular Papers，IEEE Transactions on，2012，59（3）：515-528.

［13］Clemens M Z.Quantization noise as superposition of frequency-modulated sinusoids［J］.Signal Processing Letters，IEEE ，2009，16（11）：933-936.

［14］蔡坤宝.数字信号处理［M］.北京：电子工业出版社，2011：186-188.Cai Kunbao.Digital signal processing［M］.Beijing：Publishing House of Electronics Industry，2011：186-188.