分布式双向中继系统的安全总速率优化*
王慧明 黄 芮 郑通兴
(西安交通大学电子与信息工程学院,西安,710049)
引 言
随着现代社会对信息需求的日益增长,信息传输过程中的安全性也备受关注。近20年来,以信息论为基础的物理层安全已经得到了广泛的研究。不同于传统的密钥加密算法,物理层安全利用无线信道的传输特性,直接在物理层保证了信息的安全传输。Wyner[1]于1975年提出了经典的窃听信道模型,奠定了物理层安全的研究基础。在wiretap信道模型中,如果主信道具有比窃听信道更好的信道质量,可以实现正的保密容量。原始的wiretap信道模型被进一步推广到其他窃听信道模型,比如多天线信道,协作中继信道等。其中协作通信技术已经成为实现物理层安全的一项关键技术。
协作通信通过中继节点间的协同合作提高无线传输的安全性能[2],其中协作波束形成(Cooperative beamforming,CB)和协作干扰(Cooperative jamming,CJ)是该领域的两个重要研究方向[3-4]。协作波束形成的基本思想是通过协作节点进行分布式波束形成来提高合法用户的接收信号质量;协作干扰的基本思想是通过发射人工噪声(Artificial noise,AN)信号来降低窃听方的接收信噪比(Signal-to-noise ratio,SNR)。文献[5,6]研究了基于放大转发(Amplify-and-forward,AF)协议的双向多中继网络中的协作波束形成技术,通过优化中继节点的波束形成向量和功率分配,期望可以使网络安全总速率达到最大化。为了简化问题,文献[7]提出了迫零波束形成方案(即将中继波束形成向量限定在等效窃听信道的零空间内),并且通过交替优化迭代算法,得到了最优的波束形成向量以及两个源节点的发射功率。这种迫零方案虽然有效地降低了计算复杂度,然而文献[8]指出,当窃听方接收天线数达到中继节点数量时,迫零算法的性能将急剧下降。在窃听方的信道状态信息(Channel state information,CSI)未知的情况下,文献[9,10]提出了人工噪声辅助的波束形成发射方案。此外,针对双向中继网络,文献[11]提出了混合波束形成与人工噪声的协作技术,将部分协作节点用于转发信息,而另外一部分用于发射人工噪声干扰窃听方。
在文献[6]中,作者并未考虑源节点的功率优化问题,而是假设源节点以固定功率发射信号。在文献[7]中,作者虽然优化了源节点的发射功率,但是增加了零空间的额外约束条件,从而导致安全性能下降。因此,在双向中继系统中,安全速率的最大化问题没有得到很好的解决。针对文献[6,7]的不足,本文研究了基于AF转发协议的双向多中继系统的物理层安全传输问题。本文提出了基于人工噪声的波束形成(Artificial-noise-aided beamforming,ANBF)发射方案。为了在总发射功率约束下达到最大化系统安全总速率的目标,同时优化了波束形成向量,人工噪声协方差矩阵以及两个源节点的发射功率。在ANBF方案中,通过交替迭代的思想将原优化问题转化为两个子问题,在第一个子问题中采用连续参数凸近似算法(Sequential parametric convex approximation,SPCA)[12]将原来的非凸子问题转化为一系列凸近似问题,在第二个子问题中采用牛顿迭代法进行求解,最终得到局部最优的优化结果。可以证明,现有的零空间波束形成(Null-space beamforming,NSBF)方案以及不加人工噪声的波束形成(Beamforming,BF)方案是ANBF方案的特例。仿真结果和性能分析验证了本文所提方案的有效性,并指出ANBF方案可以得到最高的安全总速率。

1 双向中继系统模型分析
1.1 双向中继系统模型
如图1所示,考虑一个双向中继通信系统,其中包括两个合法节点Tm,m=1,2,一个窃听节点E和N个可靠的中继节点Rn,n=1,2,…,N。该通信系统中的所有节点都只配备一根天线。

图1 双向中继窃听信道模型Fig.1 Two-way relay wiretap channel model
在上述通信系统中,两个合法节点希望能够在中继节点的帮助下互换信息,同时防止信息泄露给窃听方。考虑时分双工模式,并且假设信道互易。此外,假设所有的无线信道服从准静态衰落,并且全局CSI已知。文中涉及的信道系数说明如下:fR,n,gR,n,fE,gE,cE,n分别表示T1到Rn,T2到Rn,T1到E,T2到E以及Rn到E的信道系数,n=1,2,…,N。
该传输模型的信息传输过程由两个阶段组成:多接入信道(Multiple access channel,MAC)阶段和广播通信(Broadcast channel,BC)阶段。在MAC阶段,T1和T2发送各自的信息,中继节点的接收信号可以表示为

窃听节点的接收信号可以表示为
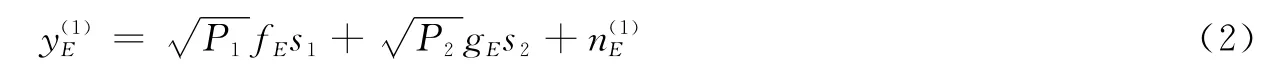
式中是窃听节点处的加性噪声。
在BC阶段,中继节点对接收的信号进行加权处理并嵌入人工噪声,然后将信息转发给源节点。中继节点的发送信号可以表示为

T1和T2节点处接收到的信号分别可以表示为

式中:w= [w1,w2,…,wN]T;FR=diag(fR);GR=diag(gR)。
同样地,在第二个阶段,窃听方的接收信号可以表示为


窃听方在两个阶段收到的信号可以表示为如下的矩阵形式

式中CE=diag(cE)。
假设所有的噪声项nT,1,nT,2,和是零均值、方差σ2的加性高斯白噪声。文中采用高斯输入和随机编码。根据文献[13]指出的双工窃听信道的可达安全速率范围,源节点T1和T2可达的安全总速率是

式中:I(;sj)表示源节点Tj到Ti的互信息,I(yE;s)表示窃听方的总互信息。
源节点T1和T2可达的安全速率分别为



窃听方的互信息可以表示为

从式(6)中可以发现,窃听方的接收模型可以等效为一个MIMO系统,其安全总速率可以表示为

基于上述讨论,将可达安全总速率表示为

在本文中,目标是通过优化P1,P2,Σ,w,使安全总速率达到最大化。直观上,由于不仅优化信号的加权向量,还优化源节点的发射功率,安全性能应该优于文献[6]中固定功率的优化结果。此外,并未对波束形成向量做类似于文献[7]中的迫零约束,所以对波束形成向量的设计可以更灵活,从而实现更优的安全性能。系统安全总速率的优化问题可以描述为


式(13b)表示总功率约束,PM表示系统总功率,P1,P2表示源节点T1和T2的发射功率,Ps=P1+P2,Tr(Σ)是中继节点发送的人工噪声总功率,PR表示中继节点发射的信号总功率,并且

优化问题(13)是一个带约束条件的非凸问题,直接求解十分复杂。本文提出了一种基于SPCA技术的高效迭代算法,通过两步交替优化得到局部最优解。
1.2 SPCA算法
采用SPCA算法[13]对中继节点的波束形成向量w和人工噪声的协方差矩阵Σ进行优化。该算法的核心思想是采用凸的上界来代替原问题中的非凸元素,使该问题可以通过现有凸优化技术求解,再通过迭代得到问题的最优解。
固定P1和P2,优化问题(13)中的目标函数可以表示为

优化问题(13)可以进一步转化为

引入辅助变量c,d和e代替式(16)中目标函数的非凸项,则优化问题可以重新表示为

引入2x的下界近似函数G(x(l),x(l-1))=2x(l-1)ln(2)(x-x(l-1))+2x(l-1),约束条件(17b,17c,17d)可以重新表示为

将式(17a)中的二次型用t1,t2和t3代替,得到

新增约束条件


采用文献[14]中复向量y对于x的一阶泰勒展开

优化问题(13)最终转化为如下的凸优化问题

该优化问题可以通过迭代算法,并且借助现有的凸优化工具箱[15]进行求解。
1.3 可行初始点的选取
采用文献[16]中提出的可行解迭代搜索算法(Iterative feasibility search algorithm,IFSA)算法选取优化问题(21)的可行初始点。具体而言,引入一个松弛变量s≥0,并且在每一步迭代过程中最小化该松弛变量,从而得到优化问题的一个可行初始点。松弛变量s的最小化问题可以描述为如下形式

证明该IFSA算法的可行性。首先将式(22a)不等号左边的部分表示为第l步的目标函数,并记为s(l)(w,Σ,c),并且将第l步的最优解表示为w(l),Σ(l)和c(l)。显然在IFSA算法迭代过程中,如果第l步的最优目标函数值小于或等于第l-1步的最优目标函数值,也就是s(l)(w(l),Σ(l),c(l))≤s(l-1)(w(l-1),Σ(l-1),c(l-1)),那么目标函数值势必随着迭代步数的增加而逐渐减小,最终收敛至0。所以将该算法的可行性证明转化为证明上述不等式成立。
由(22a)可知,将第(l-1)步最优解代入第l步,得到的目标函数值可以表示为

根 据 2x的 下 界 近 似 函 数G(x,x(l-1))= 2x(l-1)ln(2)(x-x(l-1))+2x(l-1),有 2c(l-1)≥2c(l-2)ln(2)(c(l-1)-c(l-2))+2c(l-2)。将上述不等式代入式(23),不难发现

式(24)表明第 (l-1)步最优解是第l步的一个可行解。此外,由于w(l),Σ(l)和c(l)是第l步的最优解,有

综合式(24,25),得到

式(26)的成立,说明该算法是可行性的。
类似地,由于凸函数的泰勒近似是原函数的全局下界估计,同样可以证明t1-2Re{Tr[wH(l-1)Rfg(w-w(l-1))]}-wH(l-1)Rfgw(l-1)≤s的收敛性。
至此,证明了该SPCA算法的可行性。通过求解优化问题(22),得到了可行的初始值w(0)和Σ(0)。
1.4 最优化发射功率
当得到了w和Σ值后,优化问题式(13)可以转化为



上述优化问题可以等效为如下形式

这里,和分别是P1的下界和上界。由式(8)可知,>0和>0,可以得到和

得到和之后,就可以在(,)区间内通过牛顿迭代法求得最优的P1值。
算法1 交替优化迭代算法
(1)设置两个节点的发射功率P1和P2,设定算法终止条件δ为δ=1×10-3,i=0。
(2)开始迭代:
(a)设定固定的P1和P2值,使用SPCA算法解优化问题(15),得到中继节点处的波束形成向量w和中继节点人工噪声的协方差矩阵Σ。
(b)用固定的w和Σ,通过牛顿迭代算法求解优化问题(27),得到发射功率P1和P2。
(c)将得到的w,Σ,P1和P2代入优化问题(13),得到第i步的迭代结果f(i)(w,Σ,P1,P2)。
2 零空间波束形成和无人工噪声辅助的波束形成
2.1 零空间波束形成

可达安全总速率可以表示为

在迫零约束下,优化问题(13)可以转化为

采用与前文相同的方法即可求解该优化问题,这里不再赘述。可以看出,文献[7]所采用的零空间波束形成方案是本文研究的ANBF方案的特例。
2.2 无人工噪声辅助的波束形成
讨论ANBF的另一种特殊情况——常规波束形成,即无人工噪声辅助的波束形成方案。如果不引入人工噪声,则v=0。系统可达安全总速率可以表示为

此时,优化问题(13)可以转化为

同样,采用与前文相同的方法即可求解该优化问题,这里不再赘述。可以看出,文献[6]所采用的无人工噪声的波束形成方案是本文研究的ANBF方案的特例。
3 实验仿真
仿真中所有信道参数均服从瑞利分布,所有节点高斯噪声功率为0dBW。图2描述了在不同中继节点个数时,安全总速率随着系统发射功率的变化情况。可以看到,3种方案的安全总速率均随着中继数目的增加而增大。对于任意给定的发射功率,ANBF方案的安全总速率都要高于其他两种方案。这是因为在ANBF方案中,发送的信号无需限定在等效窃听信道的零空间内,同时引入人工噪声后,中继节点可以针对性地对窃听方进行干扰,从而提高安全总速率。同时可以看到,随着中继数目的增加,NSBF和BF方法的差距在减小,这是因为NSBF算法虽然由于额外的迫零约束而减少了自由度,但更多的中继数目可以提供更高的自由度,使得NSBF自由度的减小对性能的影响变得微乎其微。
通过对比可以看到,本文提出的ANBF方案的算法复杂度与文献[7]相同,然而本文的方案由于去除了文献[7]中的迫零约束,提高了安全性能。为了验证所提ANBF方案的收敛性,图3给出了安全总速率与迭代次数的关系,其中,系统总功率为PM=20dBW。可以看到,在不同的中继数目下,经过5次迭代后,该方法都可以达到一个稳定的安全总速率值。上述仿真结果验证了该算法的收敛性,并且收敛速度与系统中继数目之间并无显著关系。

图2 安全总速率和系统发射功率的关系Fig.2 Secrecy sum rate versus system transmit power under different number of relay nodes

图3 ANBF方案中安全总速率与迭代次数的关系Fig.3 Secrecy sum rate of ANBF scheme vsrsus iterative number
4 结束语
本文研究了双向中继系统中的物理层安全传输问题。在保证系统总发射功率一定的前提下,为了最大化可达的安全总速率,本文提出了ANBF发射方案。在ANBF方案中,首先固定源节点的发射功率,采用具有收敛特性的SPCA算法,优化中继节点的波束形成向量和人工噪声协方差矩阵;再固定波束形成向量和人工噪声协方差矩阵,采用牛顿迭代法得到源节点的发射功率,通过交替迭代求得优化问题的局部最优解。作为本文方案的特例,在复杂度较低的NSBF方案中,将中继波束形成向量限定在等效窃听信道的零空间内,有效地减少了转发阶段的信息泄露,提高了通信过程的安全性;而在常规BF方案中不引入人工噪声。仿真结果和性能分析验证了本文所提方案的有效性,并指出ANBF方案可以得到比NSBF方案和常规BF方案更高的安全总速率。
[1] Wyner A D.The wire-tap channel[J].Bell System Technical Journal,1975,54(8):1355-1387.
[2] 刘琚,王超,许宏吉,等.多源多中继协作网络上行联合波束成形[J].数据采集与处理,2014,29(3):360-365.
Liu Ju,Wang Chao,Xu Hongji,et al.Optimal collaborative beamforming for multi-antenna receiver relay networks[J].Journal of Data Acquisition and Processing,2014,29(3):360-365.
[3] Wang H,Luo M,Xia X G,et al.Joint cooperative beamforming and jamming to secure AF relay systems with individual power constraint and no eavesdropper′s CSI[J].Signal Processing,IEEE Letters,2013,20(1):39-42.
[4] Dong L,Han Z,Petropulu A P,et.al.Improving wireless physical layer security via cooperative relays[J].Signal Processing,IEEE Transactions on,2009,58(3):1875-1888.
[5] Wang H,Yin Q,Xia X G.Improving the physical-layer security of wireless two-way relaying via analog network coding[C]//Global Telecommunications Conference(GLOBECOM 2011),2011IEEE.Houston,TX,USA:IEEE,2011:1-6.
[6] Wang H,Yin Q,Xia X.Distributed beamforming for physical-layer security of two-way relay networks[J].Signal Processing,IEEE Transactions on,2012,60(7):3532-3545.
[7] Yang Y,Sun C,Zhao H,et al.Algorithms for secrecy guarantee with null space beamforming in two-way relay networks[J].Signal Processing,IEEE Transactions on,2014,62(8):2111-2126.
[8] Yang Y,Li Q,Ma W,et al.Cooperative secure beamforming for AF relay networks with multiple eavesdroppers[J].Signal Processing Letters,IEEE,2012,20(1):35-38.
[9] Negi R,Goel S.Secret communication using artificial noise[C]//Vehicular Technology Conference,2005.VTC-2005-Fall.2005IEEE 62nd(Volume:3).Dallas,TX,USA:IEEE,2005:1906-1910.
[10]Goel S,Negi R.Guaranteeing secrecy using artificial noise[J].Wireless Communications,IEEE Transactions on,2008,7(6):2180-2189.
[11]Wang H,Luo M,Yin Q,et al.Hybrid cooperative beamforming and jamming for physical-layer security of two-way relay networks[J].Information Forensics and Security,IEEE Transactions on,2013,8(12):2007-2020.
[12]Amir B,Aharon B T,Luba T.A sequential parametric convex approximation method with applications to nonconvex truss topology design problems[J].Journal of Global Optimization,2010,47(1):29-51.
[13]Tekin E,Yener A.The general Gaussian multiple-access and two-way wiretap channels:achievable rates and cooperative jamming[J].Information Theory,IEEE Transactions on,2008,54(6):2735-2751.
[14]Brandwood D H.A complex gradient operator and its application in adaptive array theory[J].Communications,Radar and Signal Processing,IEE Proceedings F,1983,130(1):11-16.
[15]Grant M,Boyd S.CVX:Matlab software for disciplined convex programming[EB/OL].http://cvxr.com/cvx,2015-03-10.
[16]Yong C,Pesavento M.Joint optimization of source power allocation and distributed relay beamforming in multiuser peer-to peer relay networks[J].Signal Processing,IEEE Transactions on,2012,60(6):2962-2973.

