改进的块复制不等差错保护喷泉码＊

邓在辉 同小军 甘良才

（1.武汉纺织大学数学与计算机学院，武汉，430200；2.武汉大学电子信息学院，武汉，430072）

引 言

喷泉码由于其能很好适应信道变化和具有低的编译码复杂度而受到理论界和产业界的广泛关注，主要包括LT（Luby transform，LT）码、Raptor码［1-3］。其最初的实现方案中，所有的数据是同等被保护的，但在很多情况下，比如多媒体通信、深空通信中，部分数据需要更高的可靠性，因此设计具有不等差错保护（Unequal error protected，UEP）的喷泉码成为研究喷泉码的一个重要方面。

文献［4］首次实现了不等差错保护的喷泉码，在编码时对于给定的度分布在生成度值后，选取原始信息符号时增加重要信息比特（More important bits，MIB）的选择概率，从而提高对MIB的保护程度。文献［5］通过改变原始信息符号的选择策略来实现喷泉码的不等差错保护，让小的度值编码符号偏向MIB。文献［6］采用扩展窗方法实现喷泉码的不等差错保护性能，通过窗口包含使优先级越高的信息符号被包含的窗口越多，通过窗口的选择概率和其采用的度分布来增加对优先级高的信息符号的保护。文献［7］通过一个编码二分图来改变编码符号度值分配以及与原始信息符号的映射关系来实现喷泉码不等差错保护，其完全不能利用已有的好度分布。文献［8-9］在不改变标准喷泉码结构的基础上结合视频流的参数来实现喷泉码的不等差错保护，由于其采用了多个编码二分图，会增大总的传输冗余开销。文献［10］通过对信息符号集复制的方法来使不同优先级的信息符号的复制程度不同以实现不等差错保护，实验表明其性能整体上好于文献［4，6］中的算法。本文采用与或树工具对其性能进行分析，并在其基础上通过改变原始信息符号的选择策略，对于度为1和2的编码符号链接的原始信息符号偏向MIB，使得对MIB有更好的保护能力，而没有损失对次要信息比特（Less important bits，LIB）的保护。

1 LT码编译码原理

重复以上步骤即能产生无限的编码符号，原始信息符号和编码符号的关系如图1所示，度分布通常采用鲁棒孤子分布［1］。

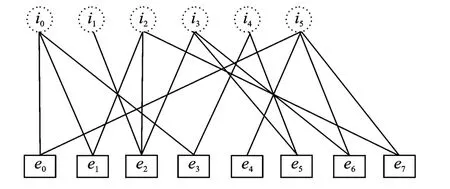
图1 LT码示意图Fig.1 Graph of LT code

其解码过程采用置信传播（Belief propagation，BP）译码算法，在由信息符号和编码符号形成的二分图中，度为1的编码符号能直接恢复出信息符号。（1）找出只有一条边连在原始符号ij的编码符号em，如果没有这样的符号，即停止译码。令ij＝em，恢复出ij。（2）对于所有的连接到ij且x≠m的编码符号ex，令ex＝ex⊕ij（⊕表示异或操作），同时去除所有连接到原始符号ij的边。

重复以上步骤即完成BP译码算法，从中可看出其译码过程为不断去边的过程，所有原始信息符号被成功解码的概率随着接收到的编码符号的增加而增加。

2 改进的块复制UEP喷泉码

传统喷泉码对信息符号的保护是等差错保护，但在许多情形下，如视频传输中往往需要其具有不等差错保护特性。

2.1 块复制UEP喷泉码

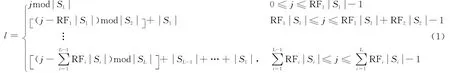
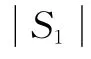
2.2 基于与或树的理论分析

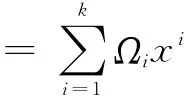
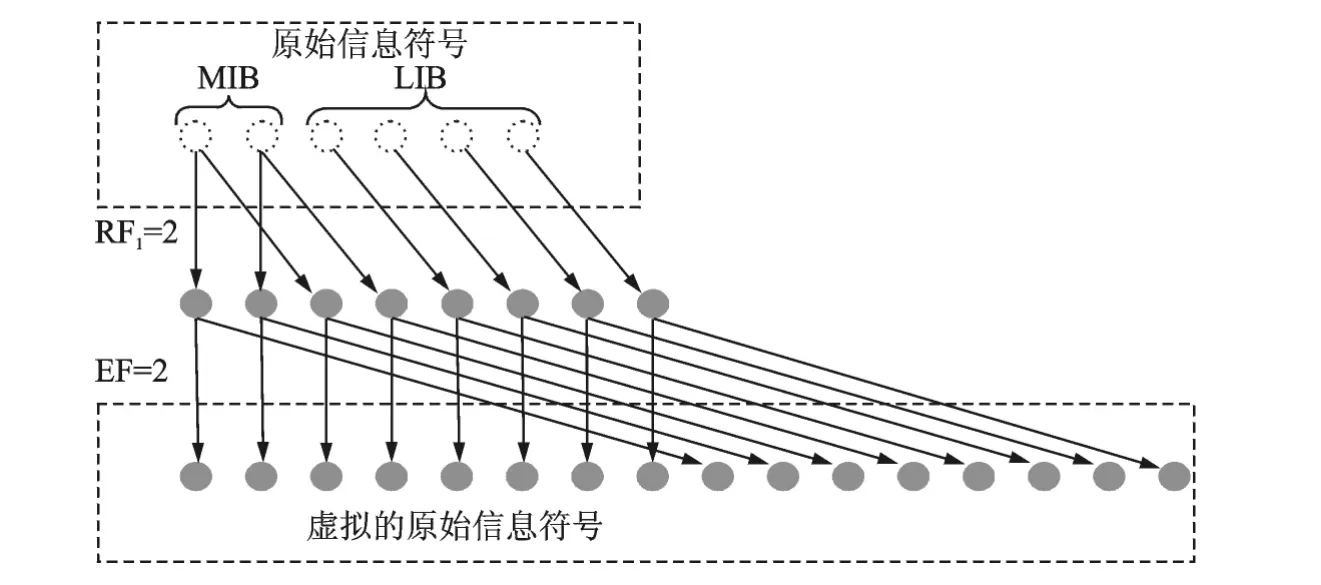
图2 块复制UEP喷泉码的虚拟原始分组构建Fig.2 Building virtual source block with UEP fountain codes based on block duplication

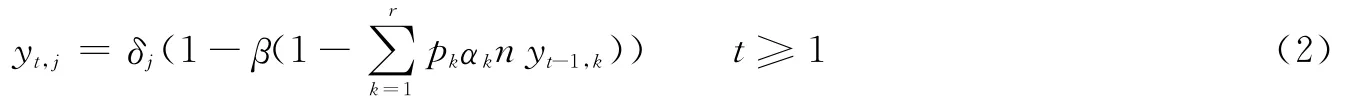
式中y0，j＝1，β（x）＝Ω′（x）／Ω′（1），μ＝Ω′（1），δj（x）＝enpjμγ（x-1）。

显然，在LT码编码过程中，原始信息符号的选择概率能决定其在译码过程中的恢复概率，只要pj＞pi，在t≥1时，则集合sj中的符号的译码成功概率就大于sj中符号的译码成功概率，满足Gt，i，j＞1。

假设原始信息符号的长度为k，其中高优先级信息符号MIB长度为h，复制因子RF1，RF2分别为R1，R2，扩展因子EF为E1，令RF2＝1，则编码过程中MIB中符号的选择概率ph，LIB中符号的选择概率pl分别为式（4）和式（5）

由于R1＞1，于是ph＞pl，据式（4）得Gt，h，l＞1，即相同次数译码迭代后，高优先级信息符号的译码概率要大于低优先级符号的译码概率，实现喷泉码不等差错保护性能。通过增加高优先级符号的选择概率能从整体上提高喷泉码的不等差错保护性能，即度数为1到截断值的编码符号中有边连接到高优先级符号的概率整体上要高于有边连接到低优先级符号的概率。

2.3 改进的块复制UEP喷泉码

文献［10］中将复制扩展的UEP和文献［4，6］中不等差错保护的性能进行比较，文献［10］中的性能在当收到大于k的编码符号时表现较好，但是，在许多应用环境中经常出现收到的编码符号数小于k，如在无线视频实时传输中，接收到的编码符号往往少于码长k，在该情况下希望能尽早地、尽量多地恢复出重要的信息比特。文献［10］通过复制扩展能从整体上改变MIB和LIB的不等保护程度，其思想本质上一方面加大了对MIB的选择概率，另一方面增加了原始信息符号的长度，从而改变了整体上的度分布。在此基础上，本文从局部上进行改进，在对信息符号的选取上改变其选取策略，而不损失整体上的不等差错保护性能。

度为1和2的编码符号对整个原始信息符号的译码起至关重要的作用，因为解码过程是从度为1的编码符号开始，所有的度为1的编码符号直接从高优先级的符号中选取，则在译码过程中，它们能被直接恢复为原始符号，而不需要等到其他的符号先被解码出来，增加了高优先级符号先于低优先级符号被解码出来的可能性，且其所占比例不能太大。并且度数越低的输出符号，其在解码过程中通过去边而成为度为1符号的可能性越大。将度为2的编码符号的一条边连接到优先级高的比特，一边连接着低优先级的原始符号，这样既保证了对优先级高的符号的优先保护，同时也使得整体的原始符号都有边能连接到，因为喷泉码的译码过程实质是不断去边的过程。改变度为1和2的原始符号选取策略从局部加大了对高优先级符号的可靠性保护，而剩下的度为2和更高度数的符号能开始低优先级符号的解码并继续下去，因此，低优先级符号的解码性能基本没有下降。

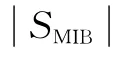
3 实验结果及分析

为了评估本文所提出算法的性能，采用与文献［10］相同的参数进行性能比较，文献［10］中算法记为块复制方法、本文算法记为改进的块复制方法，简称改进方法。假设原始信息符号长度分别为k＝1 000和k＝5 000，信息符号分为两个优先级块，其中MIB块的大小为原始信息符号长度的10%，鲁棒孤子分布的参数为c＝0.1，δ＝0.5，于是，度值为1的编码符号个数远小于MIB块原始符号个数，由于删除信道上的LT码为通用喷泉码，通信信道假设为无损信道［11］。

3.1 比特错误率的比较

采用BP算法对喷泉码进行译码，在迭代过程中，二分图中如果没有了度为1的编码符号，而且这时还有原始符号没有被译码出来，则整个译码过程结束，未被译码出来的原始符号被判决为误码。图3和图4分别反映当k为1 000和5 000时的MIB和LIB的比特错误率（Bit error rate，BER）随信息冗余长度变化的情况。BER表示错误符号个数与总符号个数的比值，即（k1-d）／k1，d表示正确解码出来的符号的个数，k1表示相应的原始符号的个数。由于LT码的编解码具有随机的特性，仿真采用多次仿真求平均值的方法，仿真次数为1 000次。

在k＝1 000时，采用与文献［10］中相同的复制因子RF1＝3，RF2＝1，扩展因子EF＝4。如图3所示，本文提出算法MIB的BER要明显好于文献［3］的仿真结果，当传输冗余开销为t′＝0.21时，MIB的BER值低于10-4，而文献［10］算法MIB的BER的值低于10-4时对应的头部开销t′为0.25，虽然对于LIB的BER相对于文献［10］中的算法有所下降，本文算法在传输冗余开销为0.38时，LIB的BER低于10-3，而文献［10］中此情况下对应的t′为0.37，但是，从图中可以看出，在相同的传输冗余开销时，两种算法对于LIB的BER而言基本相同，所以说从整体上而言，在基本没有损失LIB的性能情况下，很大程度上提高了MIB的BER性能。另外从不等恢复时间上看，所提出的算法加大MIB和LIB的译码不等恢复时间的程度。

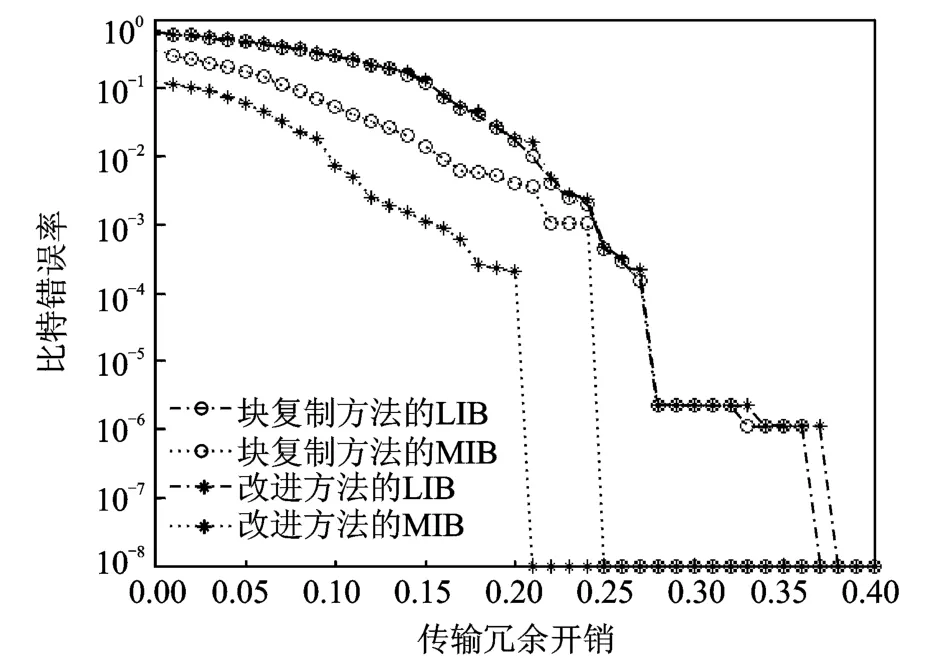
图3 不同传输冗余开销时的BER（k＝1 000）Fig.3 BER versus transmission overhead for improvement approach and method of Ref.［10］（k＝1 000）

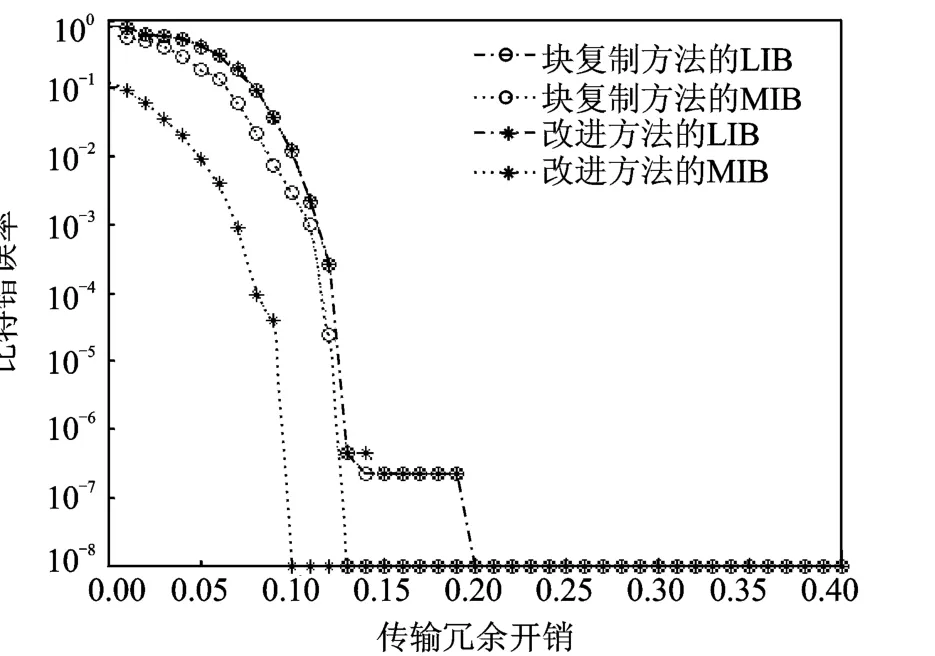
图4 不同传输冗余开销时的BER（k＝5 000）Fig.4 BER versus transmission overhead for improvement approach and method of Ref.［10］（k＝5 000）

在k＝5 000时，采用与文献［10］中相同的复制因子RF1＝2，RF2＝1和扩展因子EF＝4。如图4所示，本文提出算法MIB的BER同样要明显好于文献［10］的仿真结果，当传输冗余开销t′为0.1时，MIB的BER值低于10-5，而文献［10］中块复制算法MIB的BER值低于10-5时对应的传输冗余开销t′为0.13，同样，所提出的算法在整体上没有损失LIB的性能，两种方法都在t′＝0.2时BER值低于10-7。本文所提出的算法在于不同的码长都能更高程度地保护重要的信息比特。

3.2 高优先级符号译码失败分布比较

为评估不等差错保护方法对重要性数据的保护能力，当收到的编码符号个数少于原始信息符号个数时，通过直方图来仿真分析接收MIB数据的失败分布情况，仿真次数为1 000次。

在k＝1 000、传输冗余开销为-0.05时，高优先级符号译码失败分布如图5所示，负号表示接收到的编码符号个数小于原始符号个数。纵坐标表示发生的次数，横坐标表示还有待于译码的高优先级符号个数的百分比，反映在该冗余开销量情况下，没有译码出来的高优先级符号个数所占比重。文献［10］中算法在收到950个编码符号时，至少有95%以上的高优先级符号没有译出的次数约为28，而且，占比重最多的情况发生在70%～75%，约为140。而在本文提出改进算法中最多有70%～75%的高优先级符号未译出，且该次数为4。占比重最多的情况发生在25%～30%，约为210。比较两种方法所得出的优先级符号译码失败分布，从中可得出提出算法相比文献［10］中算法能明显加快MIB的译码，使高优先级符号得到更好的差错保护。

在k＝5 000、传输冗余开销为-0.05时，高优先级符号译码失败分布如图6所示，文献［10］中算法在收到4 500个编码符号时，至少有95%以上的高优先级符号没有译出的次数约为16，而且，占比重最多的情况发生在65%～70%，约为138。而在提出改进算法中最多有55%～60%的高优先级符号未译出，且次数为3。占比重最多的情况发生在15%～20%，约为260。从图6中可得出在k＝5 000时提出算法相比文献［10］中算法同样能明显加快高优先级符号的译码，得到了更好的不等差错保护性能。

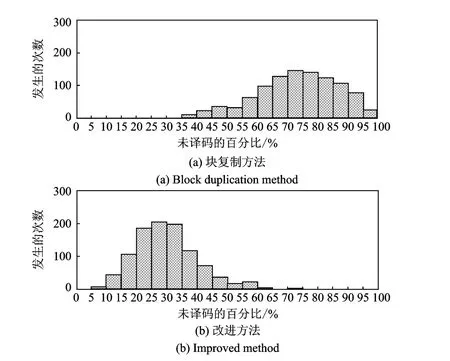
图5 MIB译码失败分布（k＝1 000）Fig.5 Histogram of failure distribution for MIB with improvement approach and method of Ref.［10］（k＝1 000）

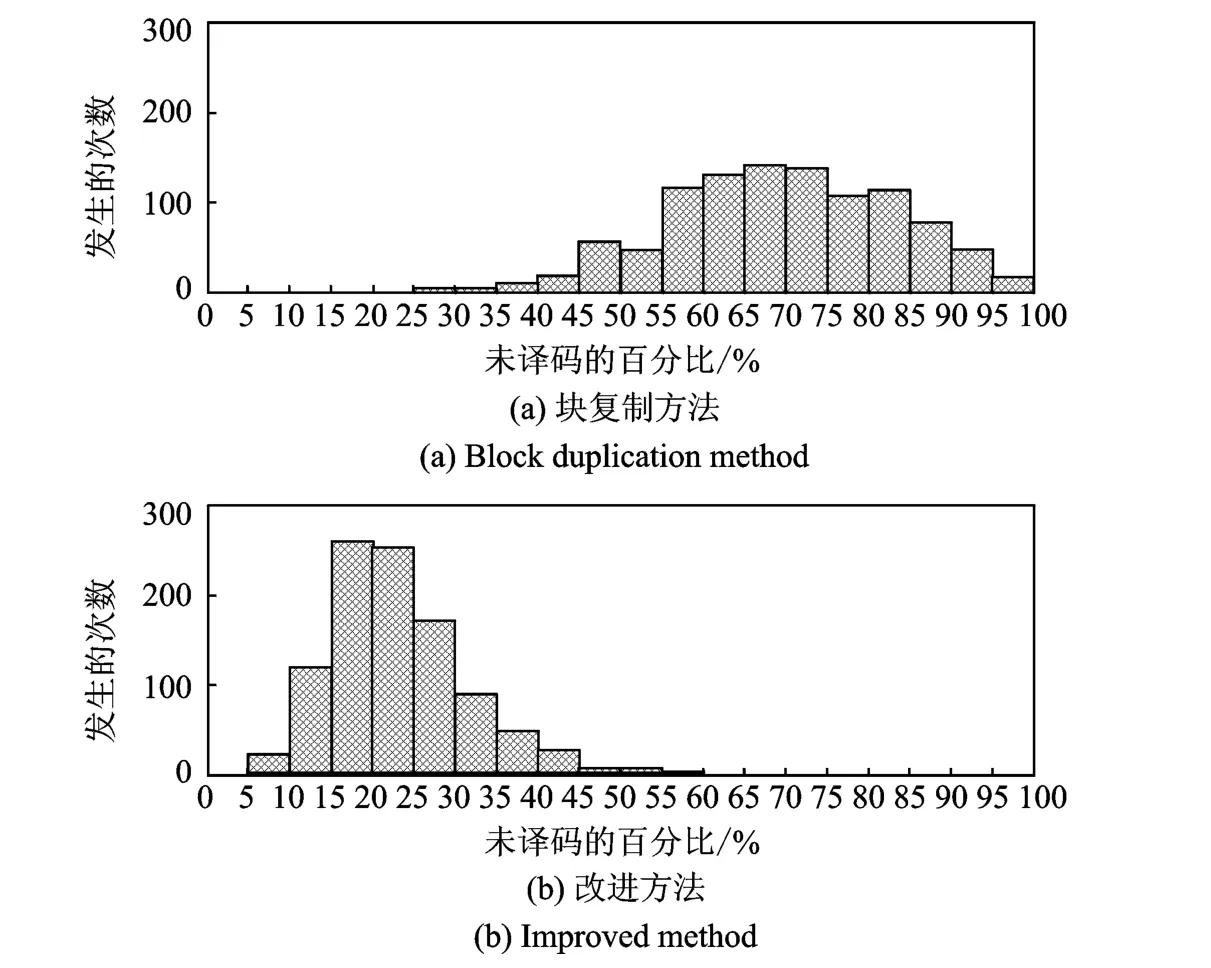
图6 MIB译码失败分布（k＝5 000）Fig.6 Histogram of failure distribution for MIB with improvement approach and method of Ref.［10］（k＝5 000）

4 结束语

本文分析了基于块复制的不等差错保护LT码的实质，在其基础上提出了改进的不等差错保护的LT码。在编码时改变了MIB和编码符号的链接策略，不仅能保持从整体上提高MIB和LIB的差错保护，同时在不损失LIB的保护基础上，能更高程度保护MIB。通过信息符号选择策略从局部增加了对MIB的保护力度，同时提升了MIB和LIB的恢复时间差别。仿真结果表明本文提出的方法要好于文献［10］中的方法。

［1］ Luby M.LT codes［C］∥Proc 2002IEEE Symp Foundations of Computer Science（FOCS）.Vancouver，Canada：IEEE，2002：271-282.

［2］ Mackay D J C.Fountain codes［J］.IEEE Proceedings Communications，2005，152（6）：1062-1068.

［3］ Shokrollahi A.Raptor codes［J］.IEEE Transactions on Information Theory，2006，52（6）：2551-2567.

［4］ Rahnavard N，Vellambi B N，Fekri F.Rateless codes with uneaual error protection protection property［J］.IEEE Transactions on Information Theory，2007，53（4）：1521-1532.

［5］ Simon S W，Cheng M K.Prioritized LT codes［C］∥Proceedings of the 42Annual Information Sciences and Systems.New Jersey，USA：［s.n.］，2008：568-573.

［6］ Vukobratovic D，Stankovic V，Sejdinovic D，et al.Scalable video multicast using expanding window fountain codes［J］.IEEE Transactions on Multimedia，2009，11（6）：1094-1104.

［7］ Cao Y，Blostein S D，Chan W Y.Unequal error protection rateless coding design for multimedia multicasting［C］∥ISIT 2010.Austin，Texas，USA：IEEE，2010：2438-2442.

［8］ Tan A S，Aksay A，Akar G B，et al.Rate-distortion optimization for stereoscopic video streaming with unequal error protection［J］.EURASIP Journal on Advances in Signal Processing，2009，2009：1-14.

［9］ Cataldi P，Grangetto M，Tillo T，et al.Sliding-window raptor codes for efficient scalable wireless video broadcasting with unequal loss protection［J］.IEEE Transactions on Image Processing，2010，19（6）：1491-1503.

［10］Ahmad S，Hanzaoui R，Al-Akaidi M.Unequal error protection using fountain codes with application to video communication［J］.IEEE Transactions on Multimedia，2011，13（1）：92-101.

［11］黄诚，易本顺.基于抛物线映射的混沌LT编码算法 ［J］.电子与信息学报，2009，31（10）：2527-2531.

Huang Cheng，Yi Benshun.Chaotic LT encoding algorithm based on parabolic map［J］.Journal of Electronics ＆Information Technology，2009，31（10）：2527-2531.