基于块稀疏快速重构的MISO活跃用户集与信道联合估计＊

康 凯 钟子发 朱然刚 王 理

（1.电子工程学院通信对抗系，合肥，230037；2.安徽省电子制约技术重点实验室，合肥，230037；3.第二炮兵工程大学信息工程系，西安，710025；4.中国人民解放军空军95865部队，北京，102218）

引 言

用户调度和下行预编码是多用户多入单出（Multi-user multi-input-single-output，MU-MISO）系统充分利用地理上分布的用户带来的丰富空间分集增益和多天线复用增益提高系统容量的关键。理想情况下，基站已知所有用户的下行信道状态信息（Channel state information，CSI），采用集中式用户选择算法并考虑用户需求和公平性等因素完成用户调度。集中式方案中CSI的获取将导致与系统内用户数成正比的上行反馈信道传输负担，基站侧测量所有用户CSI所耗时间也将随用户数目线性增长。当系统内用户数庞大时，集中式方案是不切实际的。如果限定系统工作在时分双工复用模式，则可以应用分布式方案，此方案中基站广播导频信号和信道质量信息（Channel quality information，CQI）门限，每个用户基于下行导频估计各自的信道并与进行CQI门限判决，高于门限的用户发送上行导频信号并请求接入网络，否则保持静默［1］。这样带来的好处是大大减少了上行导频信号传输所需的带宽以及基站进一步实现CSI估计和用户选择的运算量。

值得注意的是，典型的多用户通信系统在实际运行中，处于活跃状态的用户数占用户总数的比例往往比较小（请求接入网络的用户数远小于总用户数），表现为用户发送的上行信号呈现时域稀疏性，这使得基站侧利用此稀疏性并基于稀疏重构算法实现用户识别和信道估计成为可能。对这一问题的研究一般与机会式通信［2］、下行用户调度［3］和信道随机接入控制［4］有关。例如，文献［2］提出基于压缩感知（Compressed sensing，CS）的机会式接入策略，系统将用户判定是否接入信道的CQI比较门限分成多个区间（区间边界值设置由公式推导，与总用户数和用户稀疏向量的稀疏度有关），用户进行区间分布式判定是否发送预留分组包至多址接入共享信道（可以看作信道接入请求），基站稀疏重构出每一区间的强用户，随后随机选择最高活跃区间中的一个强用户接入网络并发送上行数据，最高活跃区间CQI下界即为所选择用户CQI的估计。文献［3］研究单输入单输出（Single input single output，SISO）系统，提出基站能够基于梯度投影稀疏重构算法（Gradient projection for sparse recovery，GPSR）同时得到活跃用户集及其对应的信道增益强度。文献［5，6］进一步推广到MIMO信道下行广播场景，指出基站不再局限于获取用户的CQI，当用户基于归一化的接收波束成形矢量发射上行数据时，基站能够得到各用户的信道方向信息（Channel direction information，CDI）。文献［4］从多用户 MIMO无线网络的PHY／MAC跨层设计角度进行研究，指出用户在随机接入信道时无需严格避免导频冲突，系统可以允许多个用户的多个导频流并发传输，基站利用信道冲激响应的时域稀疏性和用户活跃模式的自然稀疏性基于压缩采样匹配追踪（Compressed sampling matching pursuit，CoSaMP）可以同时获取多个用户精确的信道估计。

本文继续上述文献的工作，限定系统工作在TDD模式，设计一种特定的数据传输帧结构，基于分布式自选择过程，结合用户活跃模式自然稀疏性和信道冲激响应时延域稀疏性，将基站接收上行随机导频序列建模为稀疏线性模型，并利用稀疏矢量呈现的块稀疏特性，基于凸松弛的l2／l1模型提出一种快速的块稀疏重构算法求解问题模型，进而实现上行多用户身份识别（检测）和多用户到基站所有天线的信道估计。由于分布式自选择的用户子集大小远小于总用户数，所提方案大大减少了用于CSI估计的上行反馈信号所需的传输带宽，而且由于候选用户集的减少，基站实现用户再选择的运算量也同比下降。现有的块稀疏信号重构算法可分为两类，一类为贪婪追踪类算法，如块正交匹配追踪（Block orthogonal matching pursuit，Block OMP）［7，8］和块压缩采样匹配追踪（Block compressive sampling matching pursuit，Block CoSaMP）［9］；一类为凸松弛类算法，如基于二阶锥规划（Second-order cone programming，SOCP）和内点法（Interior point，IP）的SOCP＋IP算法［10］、基于半定规划（Semi-definite programming，SDP）和内点法的SDP＋IP算法［11］。贪婪追踪类算法的特点是计算量小，但重构误差大，并且此类算法的计算量随着块稀疏度的增大而急剧增大；凸松弛类算法的重构精度高，但是现有的基于SOCP和SDP的算法计量大，特别是在通信信号处理的实时性要求下，计算量大将是其难以实用的瓶颈。交替方向法（Alternating direction method，ADM）是一种常用的一阶优化方法，在标准稀疏重构中已经得到应用［12，13］。本文将ADM引入块稀疏信号重构中，提出一种基于ADM的块稀疏信号重构算法（Blocksparse recovery based on ADM，ADM-BSR），相比其他算法在保持重构精度的前提下，提高了计算效率。

1 数据传输帧设计与用户选择过程

MU-MISO系统工作在TDD模式，基站配置的天线数为NBS，系统内用户总数为K，且K≥NBS，用户配置单天线。本文提出如图1所示的链路数据传输帧（Frame）结构，各部分均为单比特码元长度Tb的倍数，帧长Tf小于等于信道相干时间Tc（Channel coherence time，CCT），一帧由下行导频时隙（Downlink pilot time slot，DwPTS）、保护时隙（Guard period，GP）、上行导频时隙（Uplink pilot time slot，UpPTS）、系统往返时间（Round-trip time，RTT）、有效数据传输时隙组成。其中，DwPTS用于用户接收基站广播导频并实现对各自信道的估计，GP用于避免上行／下行信号之间的干扰，UpPTS用于用户发送上行导频以供基站进行信道估计，UpPTS和RTT相加称为预留时间Tr，Tr用于用户接入网络和基站应答并在此过程中将此帧预留给最佳用户进行有效数据传输，基站需要在每一帧内选择调度Ks个用户并在RTT末端之前通知用户被选择，被选择用户与基站间将在有效数据传输时间Td内进行上行／下行数据传输。显然，由于CCT是物理信道的自然特性并界定了帧长的上界，而RTT主要由小区覆盖区域大小决定，因此减少上下行导频的数据量将有利于提高系统吞吐量。

参照图1，假定基站基于UpPTS内的上行导频已估计出所有K个用户的CQI，理论上基站可以集中式进行最优的用户选择，但是实际上运算复杂度是难以接受的［14］，而且当基站配置天线数目增加、系统内用户数庞大时，这种最优的方法基本无法实现。本文选择符合实际的次优方法，其用户选择过程分成两步完成：

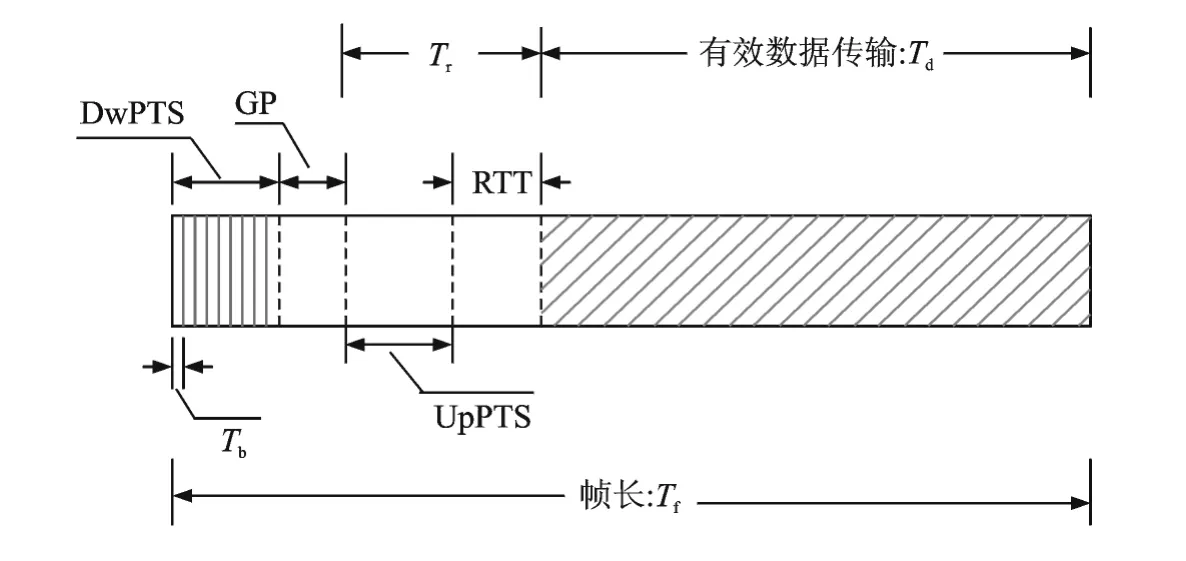
图1 链路数据传输帧结构Fig.1 Data transmission frame structure of communication link

（1）地理上随机分布的K个用户基于DwPTS内的下行导频对各自CQI进行估计，进一步用户通过将此CQI与门限值相比较并考虑用户需求进而做出是否接入网络的决定，实现分布式用户自选择，得到大小为Kss的自选择用户集（Kss≤K）。

（2）基站对自选择用户集进行再选择，得到在Td时间内传输数据的大小为Ks的选择用户集（Ks＜Kss）。

上述第一步的结果是只有一小部分用户发送上行导频并请求信道接入，基站不需要考虑所有K个用户，而只需考虑数目小了很多的Kss个用户，需处理的数据量大大减少。第二步是传统的用户选择问题，目的是按一定准则选择发送数据的用户集最大化系统利用率，例如，总吞吐量，即系统的总容量（单位bps／Hz），需要的信息是所有自选择用户的CQI，可基于最优的暴力穷尽式搜索算法或次优的选择算法，如半正交用户选择算法（Semi-orthogonal user selection，SUS）［14］，贪婪选择（Greedy user selection，GUS）［15］实现。

2 基于稀疏的活跃用户集和信道联合估计

分布式用户自选择过程的结果是Kss个用户在Tr的起始时刻要求接入网络并开始发送上行导频，基站发射端需要识别出ss个用户的集合（ss为Kss的估计），并再选择出Ks＜ss个用户（基于各用户的信道条件并考虑公平性进行调度，且保证所选择的Ks个用户为正交用户）并在RTT末端之前通知用户，且只有自选择的用户需要被通知，被通知的用户将与基站在Td时间段内进行上行／下行数据传输。在此过程中，用户再选择、上行数据相干检测以及下行波束成型（预编码）均需要对上行信道进行估计（下行信道利用信道互易性获得）。

2.1 问题模型

首先对可利用的稀疏性进行分析：

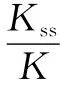
综合上述两种稀疏性，可以将用户间无协作的多址信道随机接入上行信号接收模型建立为稀疏线性模型，并基于稀疏重构方法实现信道接入多用户身份识别（检测）和信道估计（在预留时间Tr内完成）。

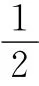
基站的每一个天线都将接收到自选择用户发送的随机标识序列（导频）激励的信道冲激响应的随机线性测量。假定随机导频序列长度等于OFDM子载波数目，导频基于独立的子载波同时发送构成一个OFDM导频符号。基站第t个天线的导频信号接收模型为

其中

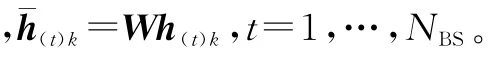
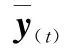
首先，参照文献［17］的做法，将复数域模型等价地变换为实数域模型，同时，为了方便公式推导，省略不相关标识并采用新的符号及索引，可得

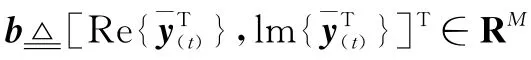
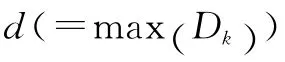
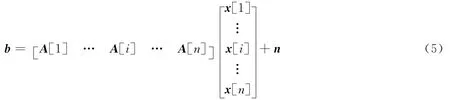
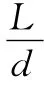
2.2 目标函数

块稀疏重构的数学模型为［10，11］

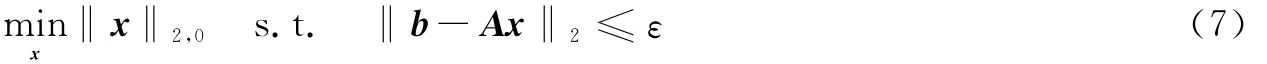
其中，ε为噪声n的均方差。直接求解上式是NP-难的［11］，一类近似求解方法是对式（7）进行凸松弛，转化为凸优化问题［10，11］，即

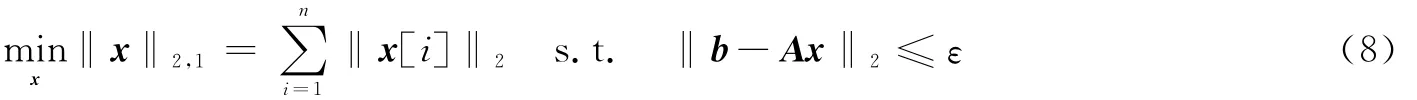
式（8）称为块稀疏重构的l2／l1模型。l2／l1模型进行块稀疏重构的优势在于高精度，但是现有的SOCP＋IP算法和SDP＋IP算法计算量大，例如SOCP＋IP的计算复杂度高达O（N3）［19］，当系统内用户数K很大时信号维数N＝KL很高，此时上述两种方法不再适用。

针对此，本文研究的目标是基于l2／l1模型提出一种快速块稀疏重构算法，在保持较高重构精度的前提下，提升计算效率。在此需要说明的是，在统计学领域Yuan利用变量成组聚集的特性，提出一种称之为group lasso［20］问题模型。在group lasso中，目标函数为

其中，τ为正则化参数。式（8）和式（9）的不同点在于，式（8）中的参数ε具有明确的物理意义，其值大小与噪声的均方差成比例，设置容易；而式（9）中的τ值则很难选择。因此，在信号处理领域研究式（8）的求解更具有实际意义。

2.3 ADM 框架

设f（x）：RM→R和g（y）：RN→R均为凸函数，B∈RP×M，C∈RP×N，w∈RP。考虑下述凸优化问题

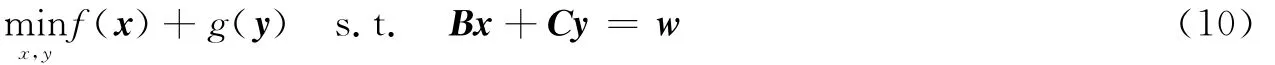
其中变量x和y在目标函数是可以分离单独求解的，而在等式约束中则是相互关联的。式（10）的增广拉格朗日函数为

其中，λ∈RP为乘子，β为惩罚因子。利用ADM求解上式的迭代形式为

2.4 基于ADM的块稀疏信号重构算法

在块稀疏信号重构l2／l1模型的基础上，利用ADM，本节提出一种快速算法，称之为ADM-BSR算法，下面详细介绍ADM-BSR算法的推导过程。对式（8）进行变量分裂，可得

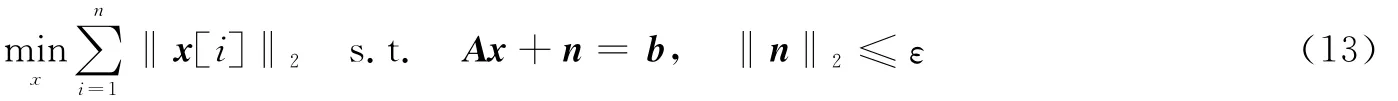
式（13）的增广拉格朗日函数为

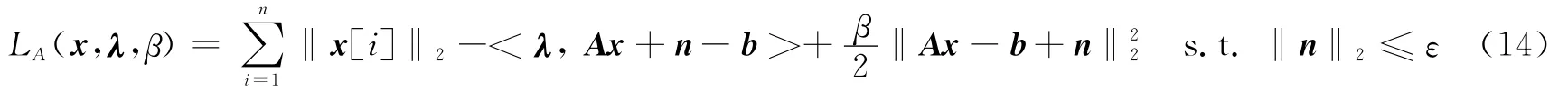
利用ADM求解式（14）的迭代形式为

式（15）的4个子问题中，nk＋1，λk＋1和βk＋1均可得到闭式解，而xk＋1只能通过迭代进行求解。考虑到x［i］，i＝1，…，n是x中互不重叠的子块，因此选择块坐标下降法（Block coordinate descent，BCD）［21］求解xk＋1。为方便描述，定义dk≜nk＋1-b-λk／βk，目标函数转化为

可见F（x）是一个非光滑的凸函数。分别针对x［i］，i＝1，…，n求次梯度，可得

其中

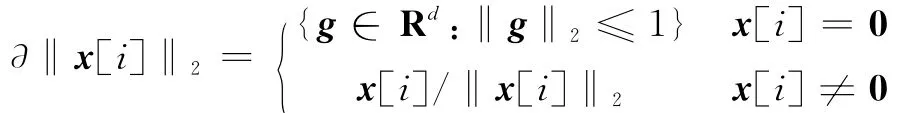
定义

因此，由式可得求解x［i］的KKT条件为

当x［i］≠0时，定义

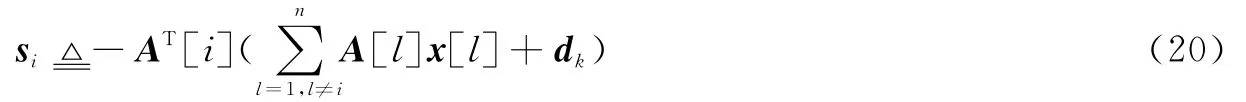
假设AT［i］A［i］＝I，这个条件不难得到，对于随机测量矩阵，对其列进行标准正交化处理后仍具有很好的性质［22］。将式（19）代入式（17），则有

由式（20）可见，si与x［i］共线，因此有

其中，如果x＞0，（x）＋＝x，否则（x）＋＝0。按照i＝1，…，n，1，…，n，1，…循环求解，直到每个x［i］均满足KKT条件。

综上分析，可以得到ADM-BSR的算法步骤。

输入：线性测量值b∈RM，感知矩阵A∈RM×N，噪声均方差ε，块长度d，块个数n＝N／d

输出：重构信号∈RN

迭代：

（1）若outLoop＝＝1，则执行（k＝1，2，…）

（2）nk＋1←PBε（λk／βk-（Axk-b））

（3）dk←nk＋1-b-λk／βk

（4）inLoop＝1，u1＝0

（5）若inLoop＝＝1，则依次执行（t＝1，2，…），否则直接跳到（13）

（6）从i＝1，…，n，依次进行

（7）根据式（18），计算ri

（8）根据式（19），判断ut［i］是否满足KKT条件，如不满足分别计算

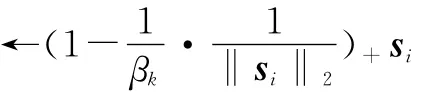
（11）t←t＋1

（12）若ut［i］，i＝1，…，n均满足 KKT条件，则令inLoop＝0，并返回5，否则返回6

（13）xk＋1［i］←ut［i］，i＝1，…，n

（14）λk＋1←λk-βk（Axk＋1＋nk＋1-b）

（15）βk＋1←γβk

（16）k←k＋1

（17）若‖b-Axk＋1‖2≤ε退出迭代，否则令outLoop＝1，返回1

2.5 ADM-BSR算法分析

（1）计算复杂度。对于某一具体问题，无法估计ADM-BSR算法所需要的迭代次数。但是对于每次迭代，从表1可以看出，ADM-BSR算法仅需要向量与标量乘积运算、向量之间相加运算、子矩阵A［l］和AT［l］与向量的乘积运算、矩阵A和向量的乘积运算，不存在矩阵与矩阵乘积运算以及矩阵求逆运算。因此，相比于SOCP＋IP算法和SDP＋IP算法，ADM-BSR算法的计算量大大减少。

（2）收敛性。首先，分析BCD方法求解xk＋1的收敛性。文献［21］中指出，若目标函数由一个光滑的凸函数和一个非光滑的块可分凸函数组成，在Gauss-Seidel循环规则下BCD方法可以收敛于问题的全局最优解。显然，求解xk＋1的目标函数F（x）满足这个要求，并且在ADM-BSR中也采取Gauss-Seidel循环规则。因此，从理论上将随着迭代次数的增加可以保证xk＋1无限接近于F（x）的全局最优解。但是，在算法的实际实施过程中迭代次数往往有限，因此xk＋1将不再是F（x）的最优解，而是次优解。这种情况下，即子问题不能精确求解时，ADM的收敛性将难以证明。然而，ADM-BSR算法中利用BCD方法迭代求解xk＋1时，以每个子块x［i］的KKT条件作为终止条件，因此可以保证xk＋1非常接近于F（x）的最优解，且在迭代过程中不会出现发散现象。因此可以预测ADM-BSR算法是收敛的，通过大量仿真也说明了这点。

3 计算机仿真

由于基站天线数为4，问题模型（式（3））的求解需要进行4次并行的稀疏重构。通过统计每一个成簇状分布的稀疏信道冲激响应中最大幅度的时延径的位置可以得到对用户索引θk，∀k的估计，进而实现活跃用户的检测并可基于，∀k参照式（3）反推出用户身份（用户与随机导频序列一一对应）。值得注意的是，由于不同天线接收到的随机导频信号均来自于相同的活跃用户，因而不同天线对应的，∀k是相同的（具有相同的块支撑集），但是不同天线对应的稀疏信道冲激响应是不同的。比较ADM-BSR，Block OMP与Block CoSaMP三种块稀疏重构算法求解活跃用户集与信道联合估计问题时在块稀疏度变化时的不同性能（块稀疏度与系统内活跃用户集的大小变化相对应，实际系统运行时，该值为随机变量但远小于总用户规模），可以得到以下仿真结果：（1）稀疏用户身份识别性能，评价指标为活跃用户集的检测概率；（2）信道估计性能，评价指标为归一化均方误差（Normalized mean square error，NMSE）；（3）计算耗时。

实验条件：设置系统内总用户数K＝512，基站天线数NBS＝4，信道长度L＝64，非零抽头数目Dk，∀k＝16，用户随机身份标识序列的长度与OFDM子载波数相同Nobs＝Nsubfreq＝128（对Nobs的设置需满足可稀疏重构要求，这与稀疏矢量的稀疏度和感知矩阵的约束等距性质（Restricted isometry property，RIP）特性有关［23］，具体分析略），信噪比设为0dB。假定基于分布式用户自选择之后有Kss＝KB＝［14：2：40］个用户的CQI估计值大于基站广播的门限，进而发送随机导频至基站并请求接入信道，仿真时KB个非零块的位置在［1，n］中随机选取，非零块中元素值服从标准高斯分布。

在ADM-BSR算法实施过程中，考虑到计算机仿真的数值精度这一因素，在采用BCD方法求解xk＋1时，对式（19）的 KKT条件进行松弛，得到

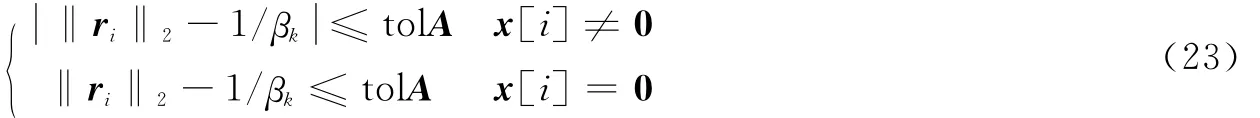
设置tolA＝0.001。仿真环境为 Matlab R2008a，P4 2.6GHz（双核），1GB内存，Windows XP操作系统。

图2～4显示的仿真曲线为50次平均的结果。从图2～4可以看出：（1）在活跃用户集的检测概率和均方误差方面，总的来看，Block OMP的性能最差，ADM-BSR和Block CoSaMP相对较好。对于ADM-BSR和Block CoSaMP，在低块稀疏度（KB＜28）时，两者的性能非常接近（检测概率为1，归一化均方误差基本相等且水平较低），但随着块稀疏度增加，ADM-BSR的性能好于Block CoSaMP。（2）在计算耗时方面，ADM-BSR算法的计算耗时随着块稀疏度增加而基本保持不变，而Block CoSaMP和Block OMP则随着块稀疏度的增加急剧增加，自Kss＝KB＝22起，ADM-BSR算法的计算耗时将小于贪婪追踪类算法。这直观说明在高块稀疏度下，ADM-BSR的计算优势十分明显。

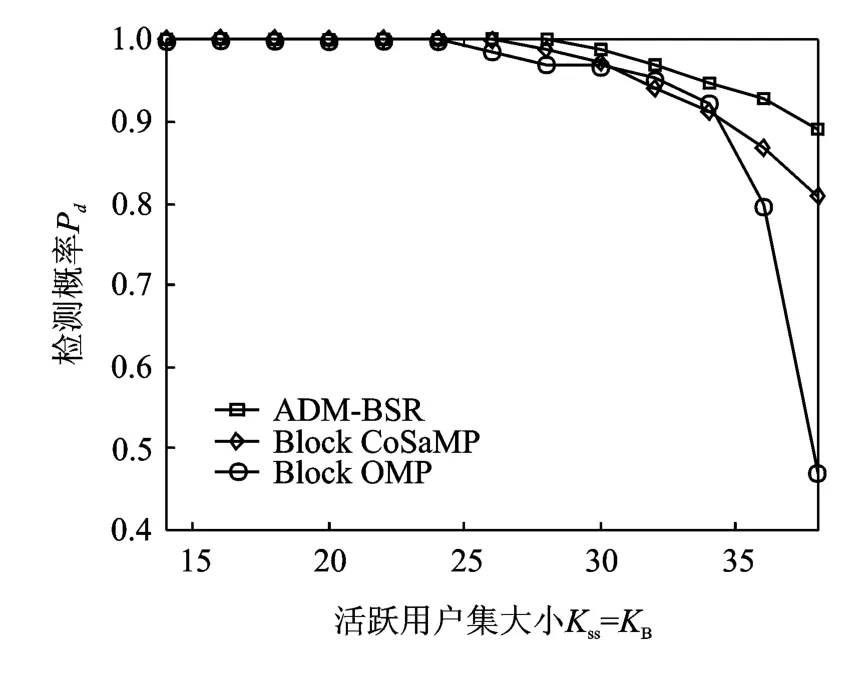
图2 检测概率随活跃用户集大小的变化Fig.2 Probability of detection versus active user set size

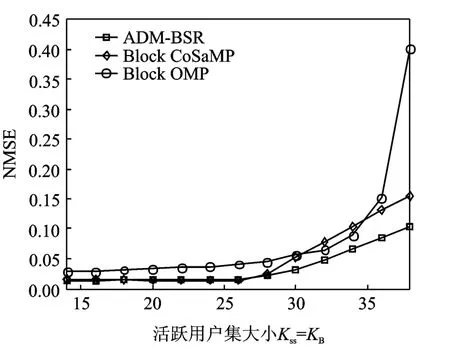
图3 归一化均方误差随活跃用户集大小的变化Fig.3 Normalized mean square error versus active user set size

图4 计算耗时随活跃用户集大小的变化Fig.4 Computing time consumption versus active user set size

4 结束语

本文研究了多用户MISO系统的用户选择与信道估计问题，提出一种新的结合用户分布式自选择信道接入策略的TDD模式数据传输帧结构设计，利用用户活跃模式的自然稀疏性和信道冲激响应时延域稀疏性基站将基站侧的活跃用户集和信道联合估计问题建模为l2／l1模型，并利用交替方向法，提出一种在保持高重构精度的前提下能够获得更快的运算效率的块稀疏重构算法（Block-sparse recovery based on ADM，ADM-BSR）求解问题模型，分析了算法的计算复杂度和收敛性。通过仿真可以看出ADM-BSR算法的重构精度高于基于贪婪追踪的Block CoSaMP和Block OMP，并且在块稀疏较高时，计算耗时也远小于这两种算法。

限于篇幅本文对稀疏多径信道条件下用户自选择过程未做详细分析。在用户自选择过程中，用户并没有是否会被选择的先验信息，且只能对各自的MISO信道进行估计（基于基站广播导频进行下行信道估计），而对其他用户的信道状态信息未知（源于用户间无协作），单用户对各自CQI的计算（一般采用可实时测量的信号干扰噪声功率比（Signal to interference and noise ratio，SINR）表征CQI参数）只与该用户自己的信道信息有关，而CQI门限值将由基站基于广播信道给出统计意义上的最佳值，目的是确定合适目标用户数Ks＜Ktar≤K。有关这部分内容的分析和对仿真感兴趣的读者可联系作者进行讨论。

参考文献：

［1］ Qin X，Berry R A.Distributed approaches for exploiting multiuser diversity in wireless networks［J］.IEEE Transactions on Information Theory，2006，52（2）：392-413.

［2］ Qaseem S T，Al-Naffouri T Y，Al-Murad T M.Compressive sensing based opportunistic protocol for exploiting multiuser diversity in wireless networks［C］∥IEEE 20th International Symposium on Personal，Indoor and Mobile Radio Communications.Riyadh，Saudi Arabia：IEEE，2009：1447-1451.

［3］ Bhaskaran S R，Davis L，Grant A，et al.Downlink scheduling using compressed sensing［C］∥IEEE Information Theory Workshop on Networking and Information Theory.Melbourne，VIC，Australia：IEEE，2009：201-205.

［4］ Lin T H，Kung H.Concurrent channel access and estimation for scalable multiuser MIMO networking［C］∥International Conference on Computer Communications.Turin，Italy：［s.n.］.2013：140-144.

［5］ Davis L M，Hanly S V，Tune P，et al.Multi-antenna downlink broadcast using compressed-sensed medium access［C］∥IEEE International Conference on Communications.Adelaide，SA，Australia：IEEE，2010：1-5.

［6］ Davis L M，Hanly S V，Tune P，et al.Channel estimation and user selection in the MIMO broadcast channel［J］.Digital Signal Processing，2011，21（5）：608-618.

［7］ Eldar C Y，Kuppinger P，Bölcsker H.Block-sparse signals：Uncertainty relations and efficient recovery［J］.IEEE Transactions Signal Processing，2010，57（6）：3042-3054.

［8］ Lv Xiaolei，Wan Chunru，Bi Guoan.Block orthogonal greedy algorithm for stable recovery of block-sparse signal representations［J］.Signal Processing，2010，90（12）：3265-3277.

［9］ Baraniuk R G，Cevher V，Duarte M F，et al.Model-based compressive sensing［J］.IEEE Transactions on Information Theory，2010，56（4）：1982-2001.

［10］Eldar C Y，Mishali M.Robust recovery of signals from a structured union of subspaces［J］.IEEE Transactions on Information Theory，2009，55（11）：5302-5316.

［11］Stojnic M，Parvaresh F，Hassibi B.On the reconstruction of block-sparse signals with an optimal number of measurements［J］.IEEE Transactions Signal Processing，2009，57（8）：3075-3085.

［12］Yang Junfeng，Zhang Yin.Alternating direction algorithms for 11-problems in compressive sensing［J］.SIAM Journal on Scientific Computing，2011，33（1）：250-278.

［13］Afonso M V，Bioucas-Dias J M，Figueiredo M A T.Fast image recovery using variable splitting and constrained optimization［J］.IEEE Transactions on Image Processing，2010，19（9）：2345-2356.

［14］Yoo T，Goldsmith A.On the optimality of multiantenna broadcast scheduling using zero-forcing beamforming［J］.IEEE Journal on Selected Areas in Communications，2006，24（3）：528-541.

［15］Dimic G，Sidiropoulos N D.On downlink beamforming with greedy user selection：Performance analysis and a simple new algorithm［J］.IEEE Transactions on Signal Processing，2005，53（10）：3857-3868.

［16］Vuokko L，Kolmonen V M，Salo J，et al.Measurement of large-scale cluster power characteristics for geometric channel models［J］.IEEE Transactions on Antennas and Propagation，2007，55（11）：3361-3365.

［17］Taubock G，Hlawatsch F.A compressed sensing technique for OFDM channel estimation in mobile environments：Exploiting channel sparsity for reducing pilots［C］∥IEEE International Conference on Acoustics Speech and Signal Processing.Hlawatsch，Frranz：IEEE，2008：2885-2888.

［18］Bajwa W U，Haupt J，Sayeed A M，et al.Compressed channel sensing：A new approach to estimating sparse multipath channels［J］.Proceedings of the IEEE，2010，98（6）：1058-1076.

［19］Rakotomamonjy A.Surveying and comparing simultaneous sparse approximation（or group-lasso）algorithms［J］.Signal Processing，2011，91（7）：1505-1526.

［20］Yuan Ming，Lin Yi.Model selection and estimation in regression with grouped variables［J］.Journal of Royal Statistical Society，Series B，2006，68（1）：49-67.

［21］Tseng P.Convergence of a block coordinate descent method for nondifferentiable minimization［J］.Journal of Optimization Theory and Applications，2001，109（3）：475-494.

［22］Candes E J，Tao T.Near-optimal signal recovery from random projections：Universal encoding strategies？［J］.IEEE Transactions on Information Theory，2006，52（12）：5406-5425.

［23］Candes E J，Romberg J K，Tao T.Stable signal recovery from incomplete and inaccurate measurements［J］.Communications on Pure and Applied Mathematics，2006，59（8）：1207-1223.