行星运动中曲率半径的分析

王璐珠

（湖南师大附中，湖南 长沙 410006）

1 问题的提出

人造地球卫星沿椭圆形轨道绕地球运行，近地点A到地球中心C的距离为r1，远地点B到地球中心的距离为r2，卫星在近地点A处的速率为vA，卫星在远地点B处的速度vB多大？

学生：利用万有引力提供向心力，

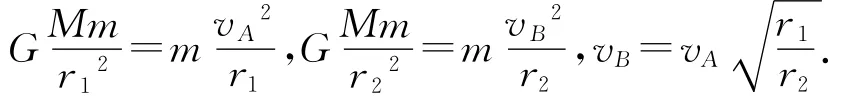
2 椭圆曲率半径的分析

思路1.（根据物理表达式分析计算）：［1］图1所示的椭圆，数学参量方程为x＝acosφ，y＝bsinφ，设质点以φ＝ωt的方式沿椭圆轨道运动，其中ω为常量，联系简谐运动知识，可得

图1

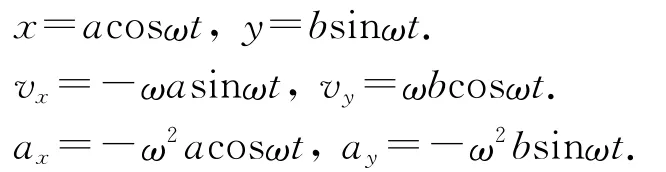
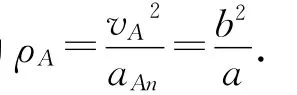
思路2.（根据对称思想定性分析）：曲线上各点的弯曲程度不同，则曲率半径也就不同，并且弯曲程度大的曲率半径越小，反之亦反.但由于椭圆轨道上的长轴两端点处对称，则曲率半径相等，可都用ρ来表示.

当学生有了正确的思路后，解法便呈现了多样性，以下是不同学生对此题的正解.

3 正确的求解

解法1.（万有引力提供向心力）

根据以上思路易证得

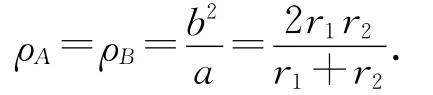
解法2.（开普勒第二定律）

学生的潜力是无限的，正向引导和开发便可找到物理世界无尽的奥妙所在.借用此题他们很快找到解决另一道类题的方法.

4 习题拓展

图2

发射地球同步卫星时，先将卫星发射至近地圆轨道1，然后经点火，使其沿椭圆轨道2运行，最后再次点火，将卫星送入同步圆轨道3，如图2，则卫星分别在1、2、3轨道上正常运行时：

（1）卫星在轨道1上经过Q点的加速度与卫星在轨道2上经过Q点加速度的大小关系.

（2）卫星在轨道1、2上经过Q的速度分别为v1、v2，卫星在轨道2、3上经过P的速度分别为v3、v4，比较这4个速度的大小.

可见，在曲线运动教学中应根据学生情况适当补充曲率圆、曲率半径的知识，并予以一定的定量分析，让其正确理解物理概念，理性分析物理情境，熟练运用物理公式，便可走出思维定势，消除“负迁移”的影响.

1 舒幼生.数学曲率半径的运动学解［J］.物理教学，2004：4－6.