基于多域特征及多传感器网络融合的滚动轴承故障诊断

任学平，辛向志，庞震，邢义通，王建国

(内蒙古科技大学 机械工程学院，内蒙古 包头 014010)

通过对滚动轴承运转状态进行检测与诊断，进而进行预知维修，可以使机械设备运行可靠性大大提升。在实际应用中，对于轴承结构与故障机理的了解，将有助于利用现代分析手段对各种故障进行有效的诊断[1]。

通常对轴承的故障诊断只是利用单一传感器采集到的振动信号进行分析，通过不同的信号处理方法分析轴承的故障特征。单一传感器只能从某一角度反映轴承的振动特征，获得的信息也是片面的。而多传感器技术及信息融合技术应用多个传感器获得不同角度的信息，再将其综合、关联估计，为全面、综合的轴承故障诊断提供了可能。因此，综合多传感器系统的优点，利用轴承多域特征作为特征向量，通过概率神经网络(Probabilistic Neural Network，PNN)进行初级诊断，然后由Dempster-Shafer(D-S)证据理论进行决策层融合诊断，可以提高故障诊断精度。

1 基本理论

1.1 滚动轴承信号特征提取

振动信号的幅值域无量纲参数可以有效反映轴承的故障特征，是特征提取的一种方法。轴承的不同故障信号表现形式及包含的信息量不同，也就是系统的不确定程度不同，而信息熵可以反映系统的不确定程度，可以作为轴承的故障特征。

1.1.1 信号幅值域无量纲特征提取

振动信号常用的幅值域统计特征参数有均值、均方根值、方根幅值、绝对平均幅值、峭度指标、峰值指标、波形指标、脉冲指标和裕度指标等，这些指标对轴承的缺陷足够敏感，但对信号幅值和频率不敏感，即与机器的工作条件无关，只取决于信号的概率密度函数p(x)[2]。无量纲参数基本不受载荷和转速等因素的影响，也无需考虑相对标准值与以前数据的对比，为取得较好的预测效果，将无量纲参数中的峭度指标Kv、峰值指标Cf、波形指标Sf、脉冲指标If、裕度指标CLf引入到特征向量之中。

1.1.2 信号的信息熵特征提取

信息熵是系统状态不确定性的定量评价指标，可以反映系统的复杂度，刻画系统的自身成分。而轴承工作过程中存在不同的故障时，其振动信号的确定性程度不同，所以信息熵值可以定量地反映轴承运行中振动信号的不确定性程度。

根据信息熵的原理及定义[3-5]，奇异谱熵、功率谱熵、小波包空间状态特征谱熵和小波包能量谱熵的构建过程如下。

(1)奇异谱熵。对单通道信号X=[x1x2…xN]采用延时嵌陷技术，将原始信号映射到嵌入空间，设空间的长度为M，则得到一个N-M行M列的轨迹矩阵A，即

(1)

对矩阵A进行奇异值分解，得到其奇异值δi，i=1,2,…,M，则δi构成了单通道振动信号的奇异值谱。奇异值谱{δi}是对振动信号时域中的一种划分。可以定义时域中信号的奇异谱熵为

(2)

式中：pi为第i个奇异值在整个奇异值谱中所占的比重。奇异谱熵反映了轴承振动能量在奇异谱划分下的不确定性。轴承故障越严重，振动信号能量越集中，正常状态下能量最分散。

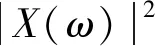
(3)

因此，S={S1，S2，…，SN}是原始信号在频域中的一种划分。则定义频域中信号的功率谱熵为

(4)

式中：pi为第i个谱值在整个功率谱中所占的比重。

功率谱熵反映了轴承振动能量在频域内的分布状况。轴承故障越严重，振动信号能量越集中于部分频率成分之中，功率谱熵值越小；正常状态下能量最分散，不确定度及功率谱熵值最大。

(3)小波变换和小波包变换都是时频分析方法，由于小波分析只对信号的低频分量进行分解，而小波包变换既对信号的低频分量进行分解，又对信号的高频部分进行分解。因此构建小波包空间状态特征谱熵和小波包能谱熵来定量描述时频域中信号的不确定性指标。

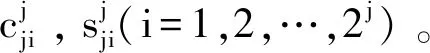
(5)

式中：s为小波包重构系数，i=2j；N为原始信号长度。原则上分解层数j选取越大，频率分辨率越高，但同时计算量增加，文中选择db4小波对信号进行分解，取j=9。则S是对信号在时频域的一种划分，对S进行奇异值分解，可以定义时频域的小波包空间状态特征谱熵为

(6)

式中：pi为第i个特征奇异值在整个特征谱中所占的比重。

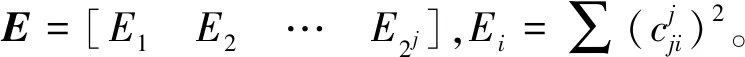
(7)

式中：pi为第i个谱值在整个小波包能谱中所占的比重。

由于小波包分析是一种时频联合分析方法，所以对信号进行小波包分解构造的小波包空间状态特征谱熵和小波包能谱熵同时反映了信号在时域和频域上的分布特征。另一方面，对S进行奇异值分解相当于将彼此关联的小波包空间映射到线性无关的特征空间，所以，小波包空间状态特征谱熵综合了冗余信号，反映了时频域中的分布不确定程度。

1.2 概率神经网络

PNN是以Parzen窗口函数为激活函数的一种前馈网络模型[6]，其融合了径向基神经网络与经典概率密度估计原理的优点，常用于模式分类。与BP神经网络相比，PNN收敛速度快，对于比较复杂的分类问题，也能得到Bayes准则下的最优解，允许增加或减少训练数据而无需重新进行长时间的训练[7]。PNN网络通常由输入层、模式层、累加层和输出层组成，其结构如图1所示。

图1 PNN网络结构图

(1)输入层每个神经元均为单输入、单输出，作用只是将输入信号X用分布的方式表示，把同样的输入值提供给模式层的所有神经元，因此其传递函数是线性的。其中X=[x1x2…xn],n为输入单元总数。

(2)模式层与输入层之间通过权值ωij相连接，该层第j个神经元的实际输入为

(8)

模式层的传递函数为

g(Zj)=exp[(Zj-1)/σ2]，

(9)

式中：σ为平滑参数。

(3)累加层将属于每一模式的概率相加，并计算每一模式的概率值。

(4)输出层将累加层的结果通过竞争函数判别输出结果。

1.3 D-S证据理论

1.3.1 基本概率分配

设Θ是一个样本空间，又称假设空间。在样本空间Θ上的基本概率分配(Basic Probability Assignment， BPA)是一个2Θ→[0,1]的函数m，称为mass函数[8-9]。并且满足

m(

(10)

其中，满足m(A)>0的A称为焦元。

信度函数Bel定义为

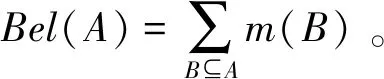
(11)

Bel(A)表示对A的信任度，也称为下线函数，表示命题成立的最小不确定性函数。

1.3.2 证据组合原理

对于∀A⊆Θ，在样本空间Θ上的有限个mass函数如m1,m2,…,mn的Dempster合成规则为

(12)

式中：K为不一致因子。

2 PNN与证据理论的融合故障诊断

基于PNN与D-S证据理论的融合轴承故障诊断流程如图2所示，主要步骤为：

图2 PNN与D-S证据理论的融合故障诊断流程图

(1)计算每个传感器信号的特征参数；

(2)将每个传感器的特征参数作为PNN的特征向量，构建3个PNN初级诊断网络；

(3)获取3个PNN的初级诊断结果；

(4)分别提取出3个PNN累加层输出结果，由D-S证据理论将其进行融合，得出最终的决策级融合诊断结论。

3 试验分析

采用机械故障综合模拟试验台研究基于振动响应的校准、平衡、共振和轴承故障等问题，试验台与传感器测点的位置如图3所示。试验选用ZonicBook/618E型测试系统，可以直接采集振动加速度、振动烈度(速度)、转速等信号，还可以对设备进行实时状态监测和频谱分析。

图3 试验平台

试验轴承型号为MB ER-10K，结构参数见表1。振动信号由安装在轴承座上的3个加速度传感器采集，信号采样频率为2 560 Hz，分析频率为1 000 Hz，分析试验数据所使用的采样个数为2 048，采样时间为0.8 s。

表1 轴承结构参数

3个加速度传感器从3个不同方向同步拾取试验轴承信号，在1 260和1 380 r/min时分别测量10组，共对4种状态(正常状态、钢球点蚀故障、内圈点蚀故障和外圈点蚀故障)轴承测得80组数据。1 260 r/min时各传感器采集的信号如图4所示(图中由上至下分别为正常、钢球故障、内圈故障及外圈故障信号)。

图4 获取信号的时域波形

将1 260 r/min时的数据作为PNN训练样本，1 380 r/min时的数据作为测试样本。从训练样本和测试样本中提取特征，分别计算5个量纲一化参数和4个信息熵值，将所有数据进行归一化处理作为PNN的输入特征向量，部分训练样本见表2。

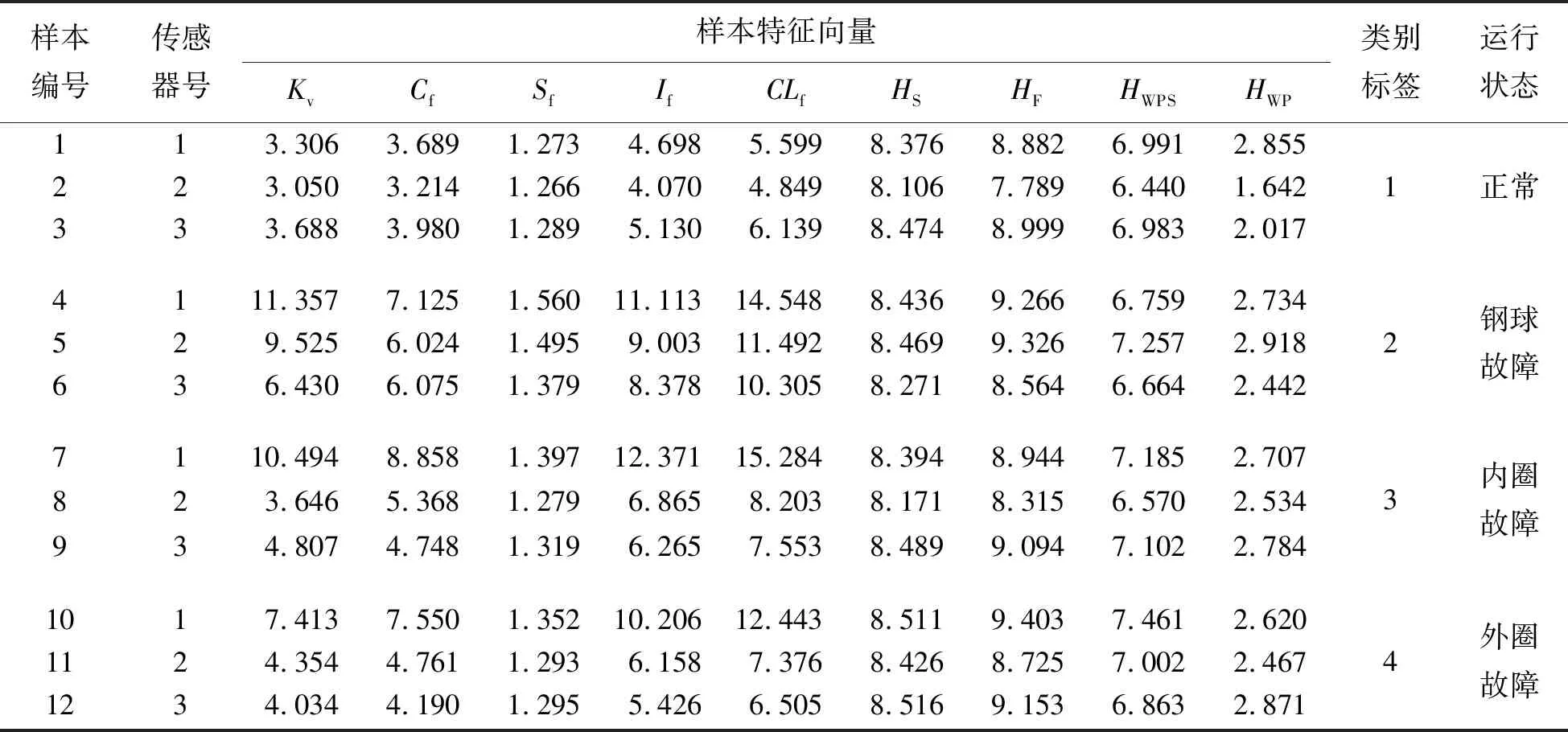
表2 量纲一化参数及信息熵特征向量样本

将3个传感器在1 260 r/min时获取的数据进行归一化处理后训练PNN1～PNN3，通过循环找到最优平滑参数为σ1=0.10，σ2=0.15，σ3=0.15，使用1 380 r/min时的数据进行测试，获取初级诊断结果。然后，对3个PNN累加层输出结果分别进行归一化并求出属于每类的概率值，将其用作构建D-S证据理论的mass函数，并将输出通过D-S证据理论融合，结果见表3。

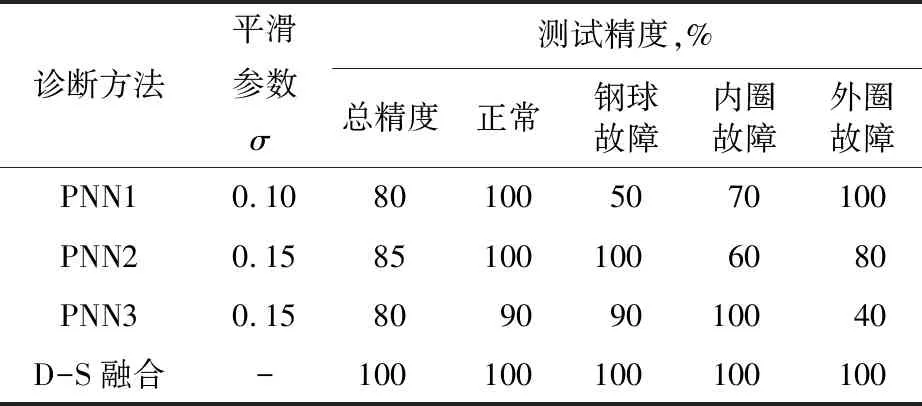
表3 小波包方法PNN测试与D-S证据理论融合识别精度

由表3可知，3个传感器对应的PNN的识别总精度以及对每种状态的识别精度均不一样。传感器1对正常和外圈故障较敏感，传感器2对正常和钢球故障较敏感，而传感器3则对内圈故障较敏感。3个PNN中总识别精度最高为85%，且存在个别识别精度很低的问题，单一网络诊断效果不是很理想。而经D-S证据理论融合后，识别总精度达到100%，效果非常理想。

为说明小波包空间状态特征谱熵和能谱熵作为PNN特征向量的优越性和多传感器网络融合的优越性，用小波空间状态特征谱熵和能谱熵[3-4]替换小波包空间状态特征谱熵和能谱熵作为特征向量，其余条件不变时的结果见表4。通过比较可见，小波包方法相对稳定，而小波方法稳定性不好，总识别精度最低只有47.5%。但经多传感器PNN网络融合决策，识别精度均能达到100%，证明融合诊断方法的可行性与容错性较好。

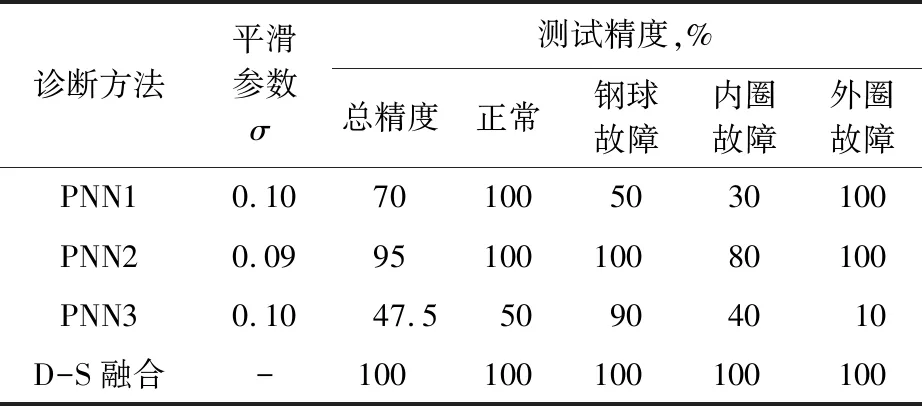
表4 小波方法PNN测试与D-S证据理论融合识别精度

4 现场轧机齿轮座诊断实例

某钢厂精轧机齿轮座在生产中出现周期性的冲击，现场怀疑为轴承故障，因此利用上述方法进行诊断。精轧机齿轮座的输入功率为4 000 kW，输入转速为75～150 r/min，在轧钢过程中进行振动测试。选用4个加速度传感器对齿轮座输入、输出轴的振动同时进行测试。加速度传感器布置在轴承端盖处，其中1#和3#沿径向放置， 2#和4#沿轴向放置，具体布置如图5所示。

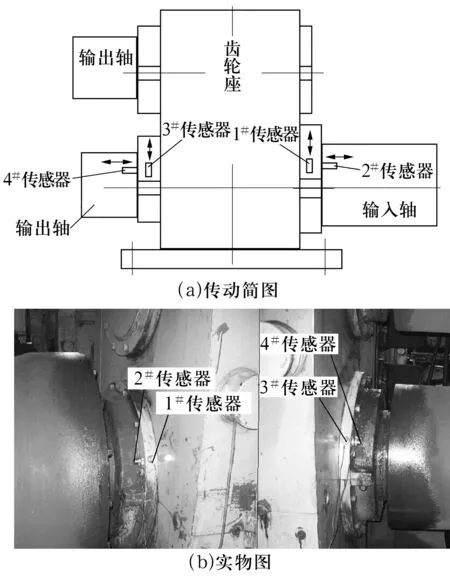
图5 精轧机齿轮座传感器测点布置图

实际测试中，采用与试验相同的采集系统，振动信号采样频率为5 120 Hz，分析频率为1 000 Hz。由于不可预知的原因，1#传感器损坏，未采集到信号，2#～4#传感器采集到振动信号的时域波形如图6所示。其中3#传感器采集信号的周期性冲击比较明显，说明精轧机振动过大，存在周期性故障。

图6 精轧机齿轮座振动信号

由于实验室轴承故障与现场轴承故障具有相似性，故可以使用试验数据分类现场数据。将2#～4#传感器分别对应前文训练好的PNN1～PNN3进行故障识别。为了与试验数据匹配相同的计算复杂度，对每个传感器取10组各2 048个采样点进行分析。首先，计算量纲一化参数及信息熵特征，输入到PNN网络进行初步诊断，部分特征向量见表5。最后，用D-S证据理论对PNN累加层结果进行融合，进行决策级的融合诊断，诊断结果见表6。

表5 精轧机齿轮座部分特征向量样本

表6 精轧机齿轮座轴承诊断结果

由表可知，PNN1和PNN2初步诊断结果可判断为正常，PNN3只有5号识别为正常，但融合诊断结果显示轴承处于正常状态。这是由于试验数据中PNN3为垂直径向数据，径向振动较大；而现场数据中PNN3为轴向数据，轴向振动相对较小。单传感器诊断结果存在差异，融合诊断能够修正差异，容错性较好。根据融合结果判断轴承无故障，经拆机检查发现轴承正常，是其他部件引起的振动，与诊断结果一致，验证了本方法的正确性，也说明多传感器网络诊断的可靠性较高。

5 结论

(1)给出了小波包空间状态特征谱熵和小波包能谱熵定义及计算方法，与小波方法相比，识别精度更高。

(2)建立了多PNN及D-S证据理论融合模型，解决了mass函数构建困难的问题，并且更符合实际。

(3)通过实验室试验和现场精轧机齿轮座实例，验证了多域特征PNN和D-S证据理论融合识别的有效性，该方法融合了不同传感器的多域特征，而且对转速不敏感，提高了轴承故障诊断的精度。