神经网络在水箱液位控制中的应用及Matlab实现

朱丽娟

（盐城师范学院 物理科学与电子技术学院，江苏 盐城 224002）

1 引言

随着控制过程复杂性的提高，控制理论的应用日益广泛。但是它的实际应用不能脱离被控对象的数学模型。然而在多数情况下，被控对象的数学模型是不知道的，或在正常运行期间模型的参数可能发生变化，因此利用控制理论去解决实际问题时，首先需要建立被控对象的数学模型，这是控制理论能否成功地用于实际的关键之一[1-3]。

系统的液位控制是当今工业生产过程中非常重要的问题，直接关系到系统经济、安全运行。常规 PID控制算法对于大部分工业过程的被控对象可取得较好的控制效果，但是对于液位控制的复杂性、变量的关联性、滞后问题，在控制液位时存在曲线振荡和精度低的缺点[4,5]，而神经网络具有并行处理、联想记忆、分布式知识存储、鲁棒性强等特性，尤其是它的自组织、自适应、自学习功能，将神经网络应用于非线性系统控制中，可以不受非线性模型的限制，便于给出工程上易于实现的学习算法。本文设计中以过程控制实验室中三容水箱控制系统为对象，采用BP神经网络的水箱液位控制算法，设计了一种基于BP神经网络液位控制系统[6,7]。

2 Labview平台的水箱液位数据采集

2.1 水箱液位控制系统

本文研究的三容水箱液位控制系统是 A3000过程控制实验系统装置，采用SIEMENS的MICROMASTER 420型变频器，LWGY型涡轮流量计，ALT-P型压力变送器，通过Labview 8.2应用软件进行动态特性测试实验操作，均采用1～5 V DC信号范围。自进水管的水通过变频器送至1号水箱，流经2号水箱最后到3号水箱，最终流入储水箱。采用开环系统，通过改变1号水箱的流量看相应的3号水箱液位变化，而流量的改变是通过变频器来实现的，所以进水流量作为输入量F，输出量为3号水箱液位h，如图1所示。

在图1中，该三容水箱比单容多了两个，产生了容量滞后，由于滞后的存在，当进水流量改变时，3号水箱的液位要经过一段时间才会发生变化，这样将会导致对扰动不能适时反应，也必然会导致较明显的超调量和超调时间，系统对周期性扰动更加敏感，很容易变得不稳定，从而造成数据采集精度的降低，影响控制精度[8]。

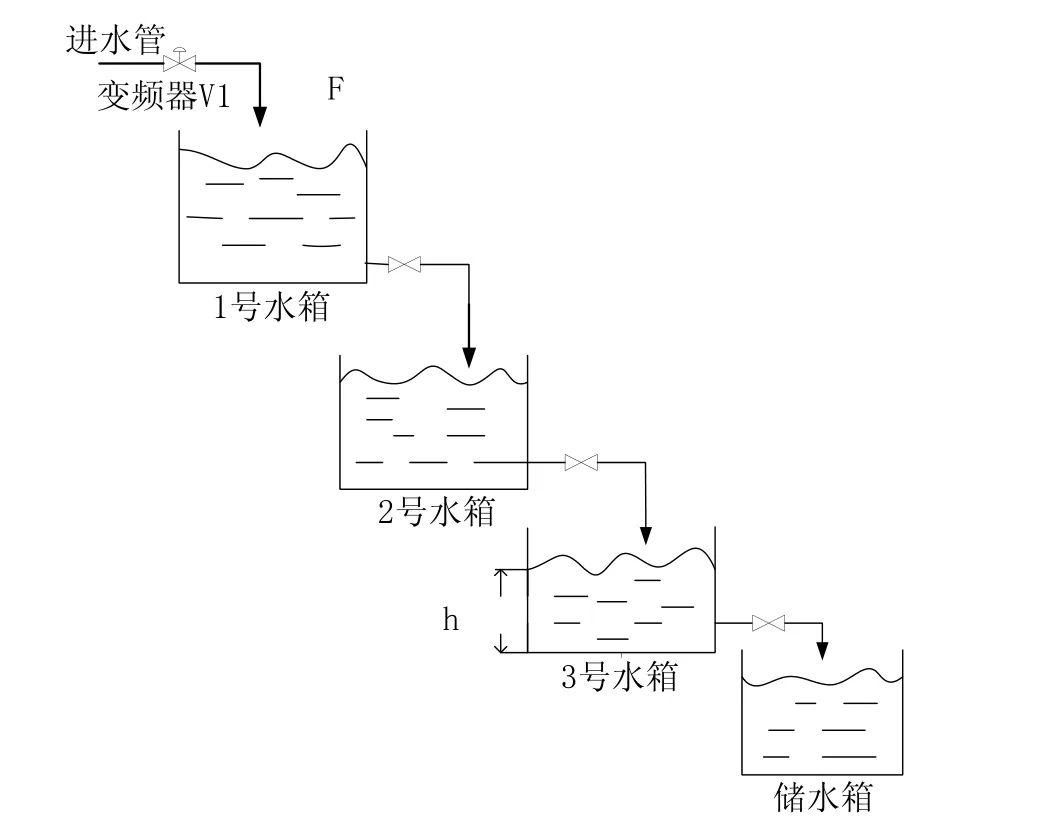
图1 三容水箱液位系统示意图

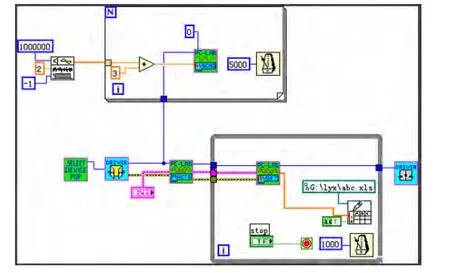
图2 Labview流程设计信号图

2.2 原始数据采集

采用LabVIEW8.2软件平台产生[-1, 1]的白噪声，如图2所示。

采样频率为1 S，变频器的信号范围是1～5 V DC，送至For循环，经过研华PCI1711接口卡的D/A通道送给变频器，信号记录到指定目录路径下的Excel文件ywkz.xls中。

液位变送器的信号经接口卡的 A/D通道信号也记录到Excel文件ywkz.xls中。

3 BP神经网络模型的确定

3.1 BP神经网络结构

BP网络（Back propagation NN）是一种单向传播的多层前向网络，如图3所示，网络除输入输出节点外，还有一层或多层的隐层节点，同层节点间没有任何耦合。输入信号从输入层节点依次传过隐层节点，最后传到输出节点。每层节点输出只影响下一层节点的输出。其节点传递函数通常为Sigmoid型，但在输出层有时为线性[9]。

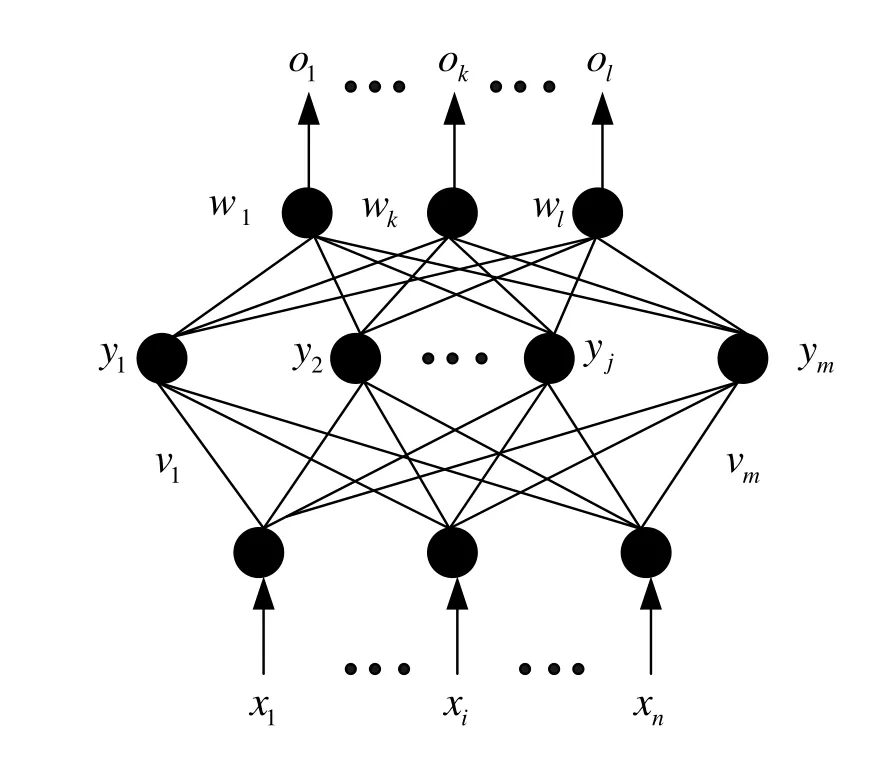
图3 BP神经网络结构图

3.2 BP网络水箱系统输入输出量确定

水箱液位控制系统作为非线性离散时间系统，通过分析只需保持现时以前3个时刻的输入输出即可，所以取(τ- 1 )~(τ-3)时刻的F0和H3作为网络的输入，即BP网络输入层，即l＝6，输出层节点数为现时刻输出流量，即输出节点为n＝1。

3.3 隐含层节点数

隐含层节点个数的设置取决于训练样本数的多少、样本噪声的大小以及样本中蕴涵规律的复杂程度。文中采用试凑法，根据式（1）

确定初始值，对本系统，

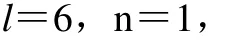
所以隐含层节点数m要大于4，经过试凑训练发现选择m＝16时训练的精度最高。

3.4 BP算法

BP算法把一组样本的输入输出问题转化为一个非线性优化问题。用迭代运算求解网络权值相当于学习记忆问题，加入隐含结点使优化问题的可调整参数增加，因此可得到更精确的解。

BP网络的权值调整使用的是反向传播的学习算法，标准的BP算法使用最速下降静态寻优算法。在修正权值时，学习过程易发生震荡，且收敛很慢；而Levenberg-Marquardt优化算法兼顾最速下降法和高斯-牛顿迭代的长处，既稳定又快速，学习时间较最速下降法短得多，经大量仿真比较，采用训练效果较好的LM算法[10]。

4 实验仿真及分析

4.1 输入输出样本选取

前 10 S训练样本数据如表 1所示。将原始数据ywkz.xls中分别按延时1、2、3秒的输入输出数据对作为输入，取前500秒的数据放在xlyb.xls作为训练样本；把测量剩下的100秒的数据对再按延时1、2、3秒放在csyb.xls作为测试样本。

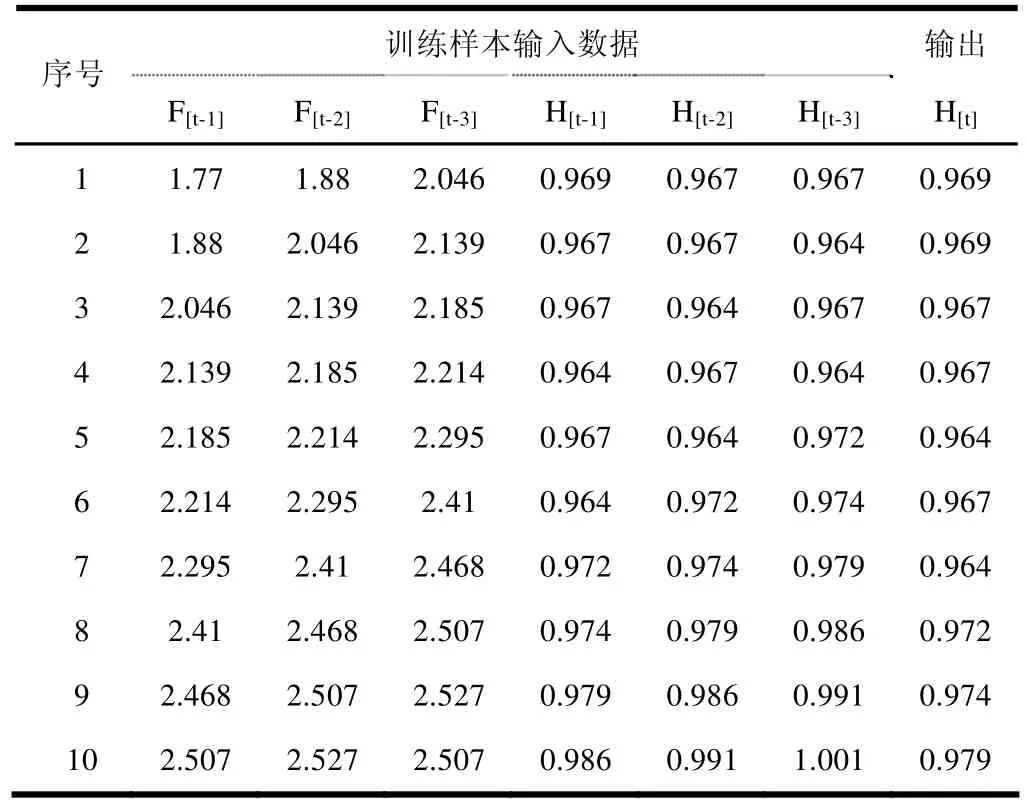
表1 训练样本数据

4.2 样本数据的预处理

样本数据如果直接用于神经网络训练，则可能导致网络不收敛，从而影响网络的性能。为了防止输入数据太大，使神经元迅速饱和而麻痹，因此必须要对样本数据进行预处理（归一化处理），本文的样本数据归一化按式（2）进行：

其中，ix表示输入或输出数据，这样就可以保证所有样本数据的绝对值波动范围在(0,1]之间，而不会影响网络的收敛问题。

4.3 仿真结果分析

利用 Matlab7.0对应的神经网络工具箱提供的newff，train函数设计M程序来建立和训练3层的BP网络水箱液位控制模型。将F[t-1]- F[t-3]、H[t-1]- H[t-3]作为输入样本，对应现时刻 H[t]作为输出样本输入到 BP神经网络中。通过大量仿真分析比较得出隐含层神经元为16个时，水箱液位的BP神经网络模型为6-16-1结构。主要语句如下：

利用已训练好神经网络对样本数据仿真结果如下：

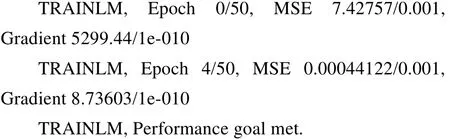
网络训练过程的误差变化曲线如图4所示，仿真测试输出曲线如图5所示。

由图4训练误差曲线可知，LM算法训练到4次就停止，达到目标精度要求。由图5的测试样本仿真响应曲线可以看出，LM算法的BP网络模型已经能很好地拟合系统的响应输出，且具有较高控制精度。结果表明，对于时滞非线性的三容水箱液位系统，采用LM算法的BP网络水箱液位控制模型能有效的控制水箱液位，并且具有较高精度。

图4 BP算法训练误差性能曲线

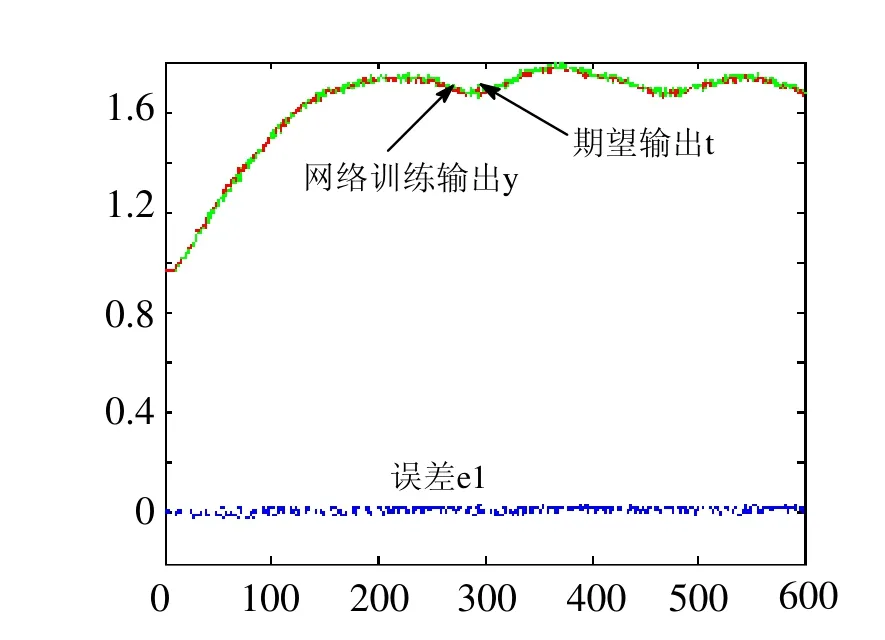
图5 LM算法归一化均方误差测试输出曲线

5 结论

由于三容水箱液位过程控制系统中，水箱液体流量与水箱液位高度之间存在着复杂、滞后的非线性映射关系，通过设计并借助Labview平台采集数据，结合Matlab工具箱函数，搭建BP神经网络水箱液位控制模型，训练拟合出流量与液位之间的关系。大量仿真曲线及实验数据表明，采用LM算法的BP神经网络模型用于水箱液位控制中是可行的，并且具有较高控制精度，能有效的用于工业生产的水箱液位过程控制中。

[1] Guoping P Liu, Visakan Kadirkamanathan, Steve A Billings.On-line identification of nonlinear system using Volterra polynominal basis function neural networks[J]. Trans Neural Networks, 1998, 11(9): 1645-1657.

[2] Yi Cheng, T W Karjala, David M Himmelblan. Closed Loop Nonlinear Process Identification Using Internally Recurrent Nets[J]. Trans Neural Networks, 1997, 10(3): 573-586.

[3] 李丽荣,韩璞,董泽.人工神经网络在系统辨识中的研究与应用[J].华北电力大学学报,2000,27(3):28-33.

[4] Kotaro Hirasawa, Shingo Mabu, Jinglu Hu. Propagation and control of stochastic through Universal Learning Networks[J]. Neural Network, 2006, 19(4): 487-499.

[5] 陈怀忠.基于BP神经网络PID算法的水箱液位控制系统设计[J].实验技术与管理,2012,29(12):81-83.

[6] 乔茂伟,韦永斌.BP基于PSO的神经网络PID在液位控制中的应用[J].自动化与仪表,2012(9):43-47.

[7] 敖茂尧.串级液位控制系统的改进粒子群神经网络PID控制研究[J].计算机测量与控制,2014,22(1):95-99.

[8] 孙红英,颜德文,李斌.基于参数自整定模糊PID的三容水箱液位控制[J].电气应用,2006,25(8):97-99.

[9] 林颐清.过程控制中被控对象神经网络模型的设计[J].山东大学学报,2002,32(2):122-126.

[10] 飞思科技产品研发中心.神经网络与MATLAB7实现[M].北京:电子工业出版社,2005:35-40.