农产品物流园区选址问题研究

牛亚宾，张明齐，高德宝

（黑龙江八一农垦大学 理学院，黑龙江 大庆 163319）

1 引言

中国是农业大国，农产品物流在国家物流体系中占有重要的地位。国内的农产品物流的发展无论在理论上还是在实践中均处于起步阶段，作为农产品物流中重要的配送环节——农产品物流园区的研究也相对比较薄弱。国内的许多学者[1]、专家[2]、企业家已注意到农产品物流研究的迫切性，开始呼吁重视农产品物流。尽管近几年国内的一些学者在农产品物流园区选址问题上做了许多的工作[3-5]，但在实用性方面还有很大的缺陷。选择合理的农产品物流园区地址是农产品物流环节的重中之重，并且农产品物流园区的选址研究对整个物流配送中心都有重要的指导意义。

农产品的流动方向主要是农村或郊区到城市，这就需要建立合适的农产品物流园区在两者之间做好桥梁。除此之外农产品的生产点和消费点比较分散，这需要物流园区作为联系点，从而具有生产到消费点的较高的运输效率和较高的商业价值。

2 模型建立

2.1 模型描述

可以将农产品物流简化成三部分：农产品原产地点，农产品物流园区和消费市场。这三部分之间的物流关系为：农产品由m个原产地点运往不同的物流园区j(j= 1 ,2,… ,n)，农场品物流园区根据各个消费市场的需求把农场品发送到各个需求市场k(k= 1 ,2,… ,p)。在清楚了农产品物流的基本过程后，我们可以根据此过程来构建降低整体费用为目标的数学模型。

2.2 基本假设

（1）农贸市场可由多个园区配送服务，且各个园区不互相周转；

（2）各个园区经调查已经确定其各方面的数据，且真实有效；

（3）运输费用与运输量和运输距离的关系均是线性关系；

（4）不考虑各个需求点的需求量变化问题。

2.3 模型分析与建立

设zj(j= 1 ,2,… ,n)表示是否在备选物流园区j建立物流园区，zj取0时不在此处建立，若取1则建立。假设经调查已经确定了n个备选物流园区，也知道了各个农产品原产地与各个物流园区的距离owdij和单位费用owcostij，各个物流园区到各个消费市场的距离wmdjk与费用wmcostjk，各个物流园区的建造固定成本concostj和单位库存费用custfreej，消费市场的需求量demandk，各个农场品原产地的供应量outputi。

以费用最小为目标，则目标函数为：

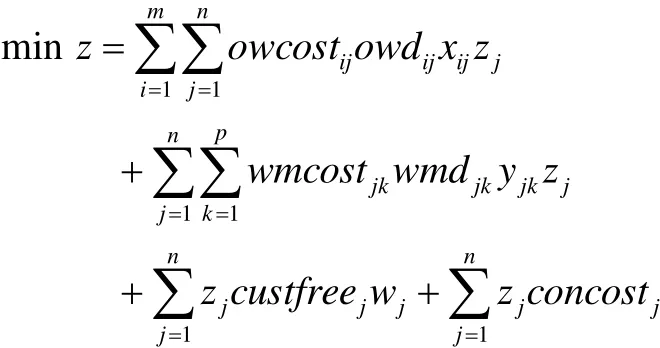
由运到各个物流园区的农产品数量小于农产品生产原地的生产量可知

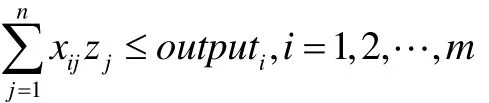
由各个物流园区获得的农产品数量大于该物流园区运出的农产品数量可知

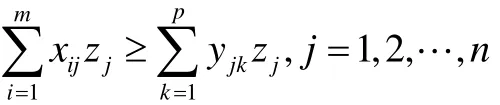
由各个消费市场得到的农产品应满足其需求量可知

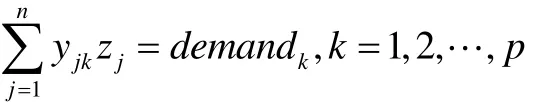
由各个农产品物流园区的库存量值可求得库存费用为

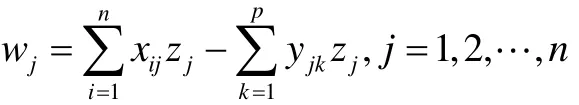
由题意可知至少应建立一个以上的农场品物流园区，故由此可知

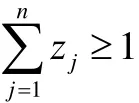
另外一个条件就是zj=0或1。

这是一个典型的混合整数规划模型。其中目标函数就是要求库存费用、运输费用、固定成本费用之和最小。

3 算法设计

针对上面所建立的数学规划模型，可以采用分支定界法来求解。利用变量jz只能取0或1两个值的特性，进行分枝。首先令全部变量取0值，检验解是否可行。若可行，已得最优解；若不可行，则令一个变量取值为0或1（此变量称为固定变量），将问题分成两个子域，其余未被指定取值的变量称为自由变量。由于这些自由变量在目标函数中的系数都是正数，因此令自由变量为0与固定变量组成的子域的解使目标函数值最小。经过几次检验，或者停止分枝，或者将第二个自由变量转为固定变量，令其值为0或1，将此子域再分成两个子域。如此继续进行，直至没有自由变量或全部子域停止分枝为止，就求出了最优解。具体计算步骤如下：

（1）令全部jz都是自由变量且取值为 0，检验解是否可行。若可行，已得最优解；若不可行，进行（2）；

（2）将某一变量转为固定变量，令其取值为 1或0，使问题分成两个子域。令一个子域中的自由变量都取0值，加上固定变量取值，组成此子域的解；

（3）计算此解的目标函数值，与已求出的可行解的最小目标函数值比较。如前者大，则不必检验其是否可行而停止分枝，若子域都检验过，转（7），否则转（6）。因继续分枝即使得到可行解，其目标函数值也较大，不会是最优解；如前者小，进行（4）。对第一次算出的目标函数值，不必进行比较，直接转（4）；

（4）检验解是否可行。如可行，已得一个可行解，计算并记下它的z值，并停止分枝。若子域都检验过，转（7），否则转（6）。因继续分枝，即使得到可行解，目标函数值也比记下的z值大，不会是最优解；如不可行，进行（5）；

（5）将子域固定变量的值代入第一个不等式约束条件方程，并令不等式左端的自由变量当系数为负时取值为1，系数为正时取值为0，这就是左端所能取的最小值。若此最小值大于右端值，则此子域为不可行子域，不再往下分枝。若子域都检验过，转（7），否则转（6）；若此最小值小于右端值，则依次检验下一个不等式约束方程，直至所有的不等式约束方程都通过。若子域都检验过，转（7），否则转（6）；

（6）定出尚未检验过的另一个子域的解，进行（3）至（5），若所有子域都停止分枝，计算停止，目标函数值最小的可行解就是最优解；否则，转（7）；

（7）检查有无自由变量。若有，转（2）；若没有，计算停止。目标函数值最小的可行解就是最优解。由于（3）、（4）、（5）中都有停止分枝的情况，对这些子域自由变量取值为0或1的一切可能组合都被隐含地考虑过了，不必再一一列举。所以，这种方法与穷举法比较，计算量可大大减少。

注意，要应用这种算法，0-1规划模型必须是下述标准型：所有约束条件方程必须是“≤”型式。如果0-1规划模型不是标准型式，则可作下述变换，使其转为标准型式：（1）如目标函数是求最大，可将目标函数乘-1并求最小；（2）如约束条件方程是“≥”型式，可将不等式两端乘-1，变换为“≤”型式；（3）如约束条件方程是“=”型式，则将它变换为一个“≤”型式和一个“≥”型式的约束条件方程，并对后一方程两端乘-1，使其成为“≤”型式。

4 案例分析

根据大庆市拟建的几个农场品物流园区，我们调查了3个农场品物流园区待选地址，有4个农产品原产地，6个消费市场，并且得到了相关数据（见表1与表2，其中距离单位为 Km，单位运费单位为元·Km·t-1，原产地供应量单位为t，农贸市场需求量单位为t，库存费用单位为元·t-1，建造成本单位为元）。根据我们所建立的模型进行案例仿真，运用所设计的算法进行求解，在此我们借助lingo软件进行编程求解，得到如下结果：由lingo运行结果可知当我们选取 1号地址为农产品物流园区地址时的费用最小为394 197.3元。

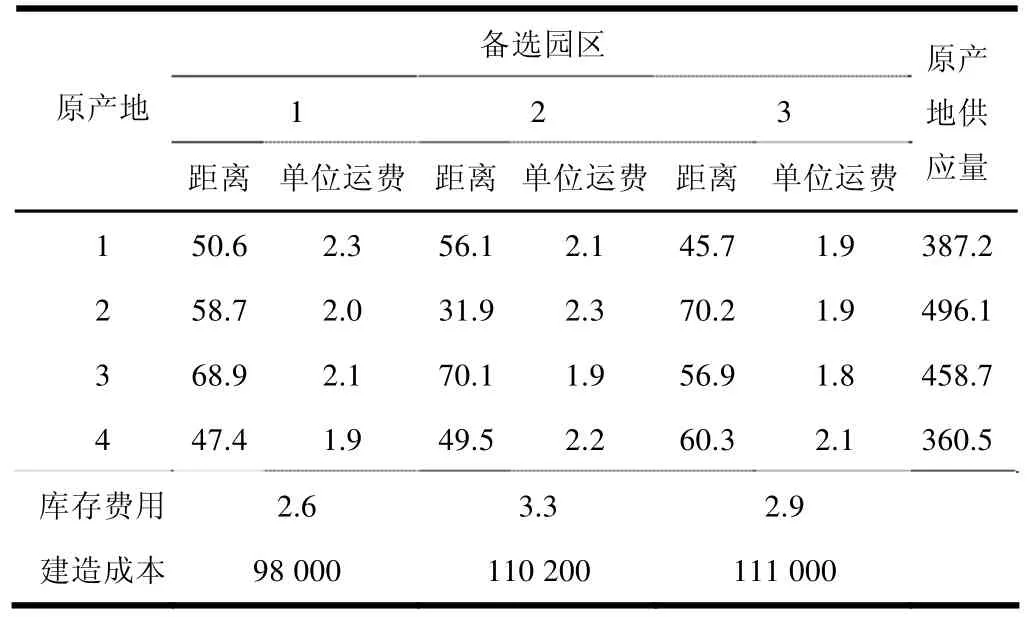
表1 原产地到备选园区的距离及单位运费

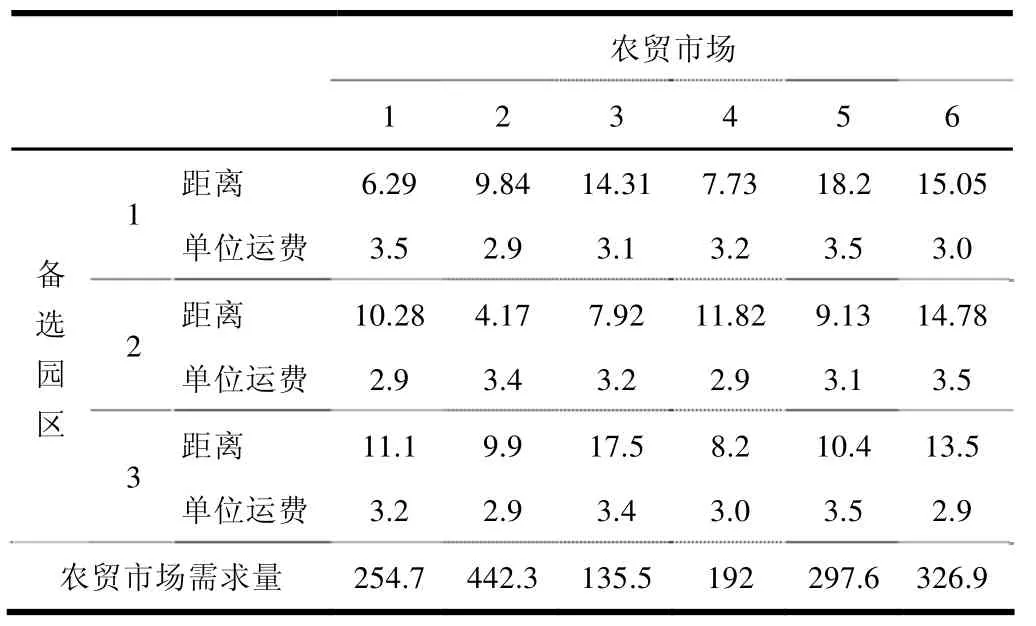
表2 备选园区到农贸市场的距离及单位运费

5 结论

本文采用0-1线性规划来解决农产品物流园区的选址问题，考虑到了有关选址问题的一些基本因素，以较小的费用为目标可以很好地选取较佳的农产品物流园区地址，并且模型求解的所需的数据比较容易获得。我们所使用的分枝定界算法可以很好地解决本文所建立的模型，该算法计算快，可以很好地得出我们想要的结果，并且这种方法不必评价所有可能的操作变量组合而找到最优解。但是，在建立模型时我们并没有考虑到不同农产品具有不同的保鲜期和季节性等特点，在这方面有待进一步改进。

[1] 李兴福.基于第三方物流的大连市农村物流问题研究[D].大连海事大学,2011:33-40.

[2] 刘伟.农产品物流配送中心选址问题研究[J].决策与信息(财经观察),2008,45(9):28-29.

[3] 李楠.农产品物流中心选址问题研究[D].北京交通大学,2009:33-41.

[4] 王林,叶小侠.基于Lingo语言求解物流配送中心选址模型[J].物流技术,2008,27(10):113-115.

[5] 穆英红,王爱云.基于非线性规划的农产品物流园区选址模型[J].山东师范大学学报(自然科学版),2013,28(1):41-43.