OFDM/OFDMA 系统的时域同步干扰方案的研究
张昊,夏文龙,郭庆功
OFDM/OFDMA 系统的时域同步干扰方案的研究
张昊,夏文龙,郭庆功
正交频分复用技术具有频谱利用率高、抗多径能力强、信息传输速率高等优点,已成为第四代移动通信的核心技术,因此,在保密环境下对OFDM通信系统的有效干扰研究也更加迫切。OFDM/OFDMA系统在接收端需要进行准确的定时同步后,才能获得更高的通信质量。常用的同步算法有Schmidl算法、Minn算法和Park算法。针对Minn算法和Park算法这两种OFDM时域同步算法进行了时域干扰方案的研究,最后,通过仿真验证方案的有效性。
OFDM;干扰;时域;同步算法
0 引言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)系统凭借其优秀的性能,广泛应用于无线通信领域中,随着第四代通信技术的普及,为满足特殊保密环境的要求针对OFDM通信系统的高效干扰研究也变得日益迫切。陈西宏、单超等主要研究了多音干扰对OFDM系统干扰效果[1-2],Charles主要研究了对导频音进行消除处理后的干扰效果[3-4]。文献[1]-[4]干扰方案的局限性在于要掌握信道信息且仅适用于快衰落梳状导频OFDM系统,若用于慢衰落块状导频OFDM系统则干扰效果将会降低很多。Matthew等提出了几种OFDM系统对用于时域同步的前导序列干扰的方案[5],此类干扰方案不需要掌握信道信息,且同样适用于慢衰落块状导频OFDM系统,但是只针对Schmidl这一种同步算法进行了研究,而常见的同步算法有Schmidl算法、Minn算法、Park算法。本文首先分析同步算法的数学模型,在此基础上研究了时域干扰对于Minn和Park两种同步算法进行干扰的机制,最后采用Matlab仿真验证了结果的有效性。
1 方案设计
OFDM接收系统框图如图1所示:
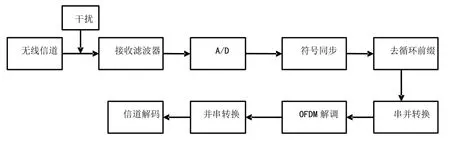
图1 OFDM接收系统框图
系统在进行去循环前缀之前需要进行时域同步以确定循环前缀的准确位置,才能较好的恢复出原有的信息。故本文通过对系统同步过程进行时域干扰,破坏系统的符号定时以达到降低整个接收系统通信质量的目的。
1.1 同步算法
OFDM系统同步有3个组成部分,符号定时、载波频偏估计和校正。同步算法主要包括基于训练序列的算法,基于循环前缀(CP)的算法和盲同步算法。由于盲同步算法较为复杂且可实现性较低,基于CP的算法只能用于符号定时,不能用于帧同步,故本文主要分析基于训练序列的算法。常用的同步算法有Schmidl算法,Minn算法和Park算法。
Timothy M. Schmidl 和 Donald C.Cox提出了一种利用前后两半相同的序列进行定时估计的方法。其训练序列的结构如图2所示:
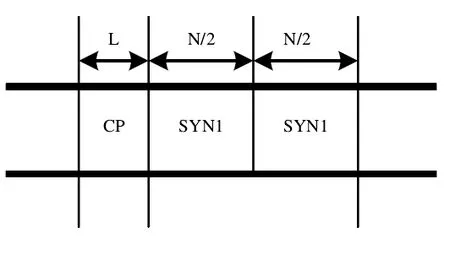
图2 Schmidl算法前导序列结构
此序列的结构可以用在 OFDM 发送端 IFFT 变换之前,在偶数子载波上发射伪噪声序列,奇数子载波上发射0,再经过 IFFT 变换后实现。从图2中可以看出,此训练序列前后两半是相同的,长度均为 N/2,CP为训练符号的循环前缀。
算法描述为:假设接收序列为 r(n) ,则构造以下检测函数位公式(1)、(2)、(3):
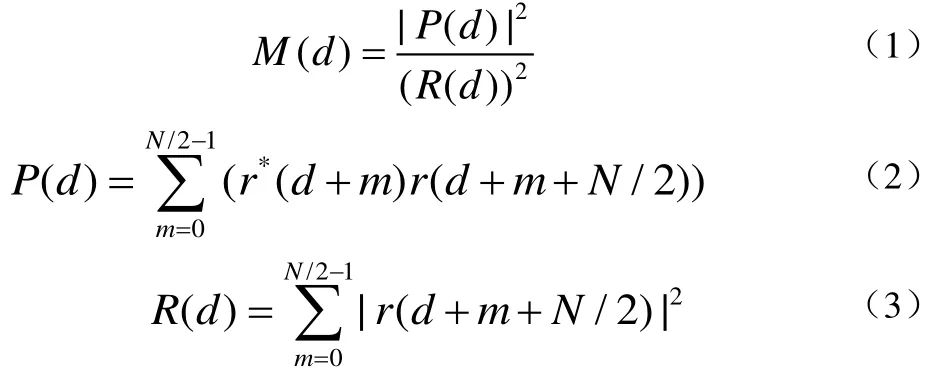
其中,R(d)是指前导序列的后半段能量,是P(d)函数的归一化能量值,P(d)函数是滑动窗内前半段序列与后半段序列的互相关值,当前半段序列与后半段序列结构相同时,即相关值峰值检测函数M(d)达到最大时,可以定位出OFDM符号的起始位置。
由于接收前导训练序列后,前后两段序列互相关性比较高,所以M(d)会产生一个互相关峰值平台区,从而增大了定时误差。
正因为Schmidl算法存在“先天性”的定时误差,所以Minn算法被提出。此训练序列结构如图3所示:

图3 Minn算法前导序列结构
检测函数与Schmidl算法相同。而能量互相关函数P(d)与能量归一化函数R(d)同Schmidl算法有所不同,如公式(4)、(5):
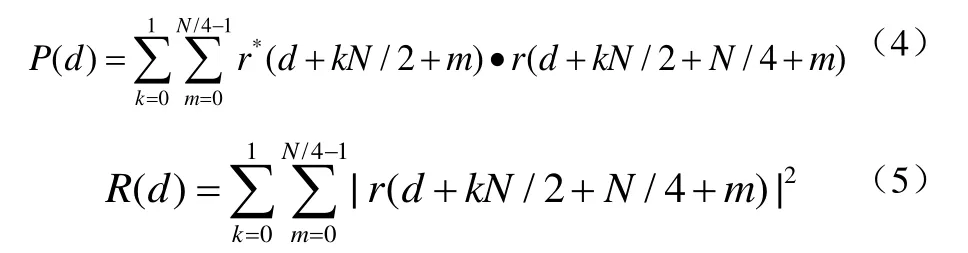
由于Minn算法前后两半序列是相反的,因此当滑动起始点在CP内时,因为CP内序列的符号和前半序列中序列的符号也是相反的,因此窗口在CP内部分的值就是负值,这样就不会出现平台区,提高了定时精度。
Minn算法虽然消除平台区,但是由于存在较多副峰值,所以在进行最大值判决时也容易对判决器产生干扰,从而影响定时的准确性。
Park算法的提出就消除了诸多副峰,只保留了一个峰值,训练序列结构如图4所示:

图4 Park算法序列结构
其中C与C*,D与D*互为共轭序列,C与D互为逆序列。
此时,构造检测函数为如式所公式(1)所示:
相关能量函数和窗口能量函数分别为公式(6)、(7):
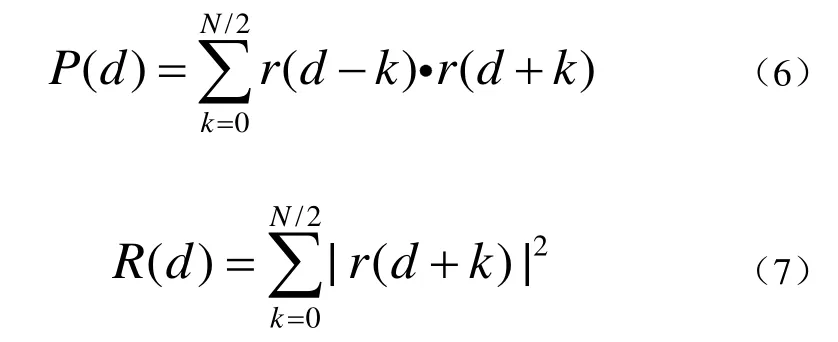
在AWGN信道下的检测函数波形来看,Schmidl算法因为具有平台现象,因此定时偏差最大,Park 算法最为稳定,检测定时偏差最小,如图5所示:
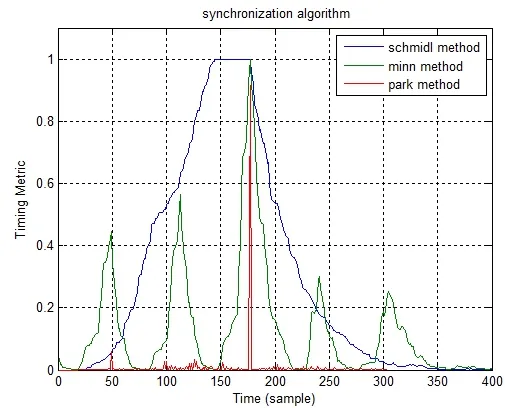
图5 三种算法M(d)波形比较
1.2 干扰分析
由于OFDM系统对频率偏移十分敏感,而导频音常常被用来做信道估计和插值依据,所以常见的高效率干扰方案为多音在导频处的干扰方案,但导频音干扰方案若想达到较好的干扰效果,难度较大,故而本文研究了针对时域OFDM前导符号的干扰。常见的3种同步算法中对Minn算法和Park算法的干扰比较少见,所以本文研究针对这两种算法的干扰。
1.2.1 前导序列白噪化
以往的宽带白噪声干扰是对全时域所有OFDM进行连续时间的噪声干扰。该方法是对宽带白噪声连续干扰的改进。
假设高斯白噪声n(t),服从均值为0,方差为1的高斯分布,即满足公式(8):
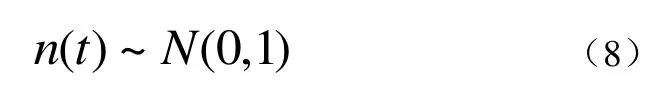
那么接收信号表示为公式(9):
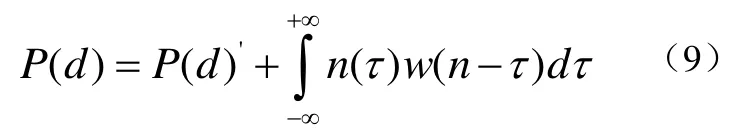
从(9)式可以看出,该干扰手段其主要目的是影响M(d)的幅值,以降低M(d)幅值到判决器阈值以下,从而影响这个OFDM系统的同步。
1.2.2 伪前导序列时域干扰
该方法是基于同步相关算法,使用伪前导序列对接收机进行干扰,以期达到移动M(d)的峰值或者大幅衰减峰值的目的,使整个系统发生定时错误。
对于Minn算法,时域自相关矩阵由(5)式可得,伪前导序列可以由原前导序列进行延时处理得到,也可以是由PN序列组成[5]。本文中选择前导序列循环移位来生成伪前导序列,所以伪前导序列表达式为公式(10):
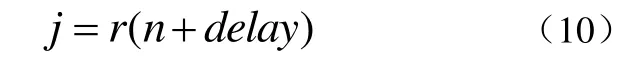
那么接收机接收信号则为公式(11):
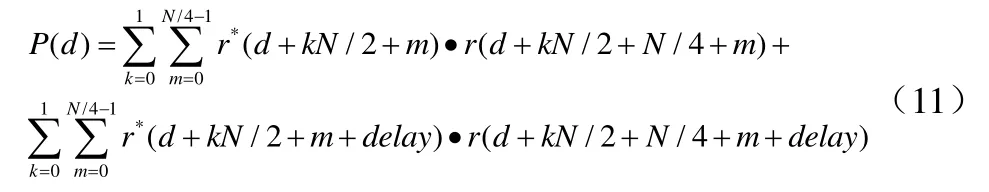
由于Minn算法前导序列结构,根据(11)式,为了简化计算,令k=0,那么可以得到公式(12):
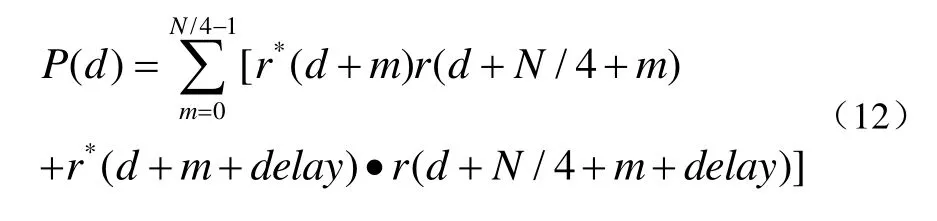
对于Park算法,根据序列结构与式(7)可知,在窗口宽度为N/2条件下,互为共轭,若,那么接收信号与之间的共轭关系被破坏,则M(d)无明显峰值。
1.2.3 前导序列消除
最后一种方法是干扰机在与发射机处于时间上的同步状态时,发射与原前导序列相位相反的序列,从而使接收机接收到的前导序列趋于0,使式(7)中分子为0,从而相关算法过后得到M(d)的幅值也趋于0,致使整个系统无法进行定时。这种方法需要准确的掌握前导序列的信息,并且要求干扰机信道与发射机信道保持一定的一致性,这样才能达到较好的干扰效果。
对于Minn算法,时域自相关矩阵由(5)式可知,干扰信号为公式(13):

则接收序列为公式(14):
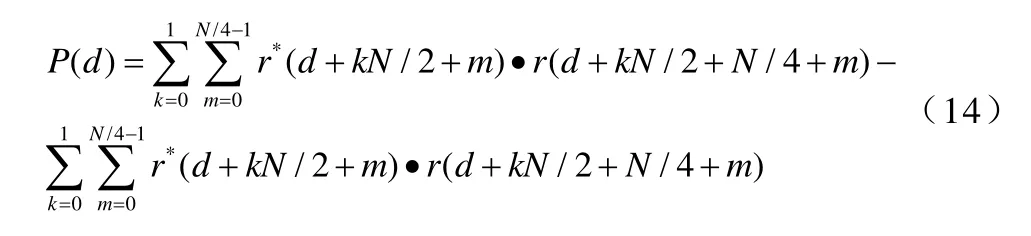
由(14)式可知,P(d)结果趋于0,M(d)没有明显峰值。对于Park算法同理可得。
2 干扰方案仿真
这部分主要是基于Matlab仿真对前导白噪化、伪前导序列时域干扰、前导序列消除三种算法进行了仿真的验证,几种仿真环境中,信干比统一设置为0dB。
2.1 前导白噪化仿真
该方法需要掌握发射机发送信息的帧结构。白噪声分别对Minn算法的前导序列进行干扰,如图6所示:
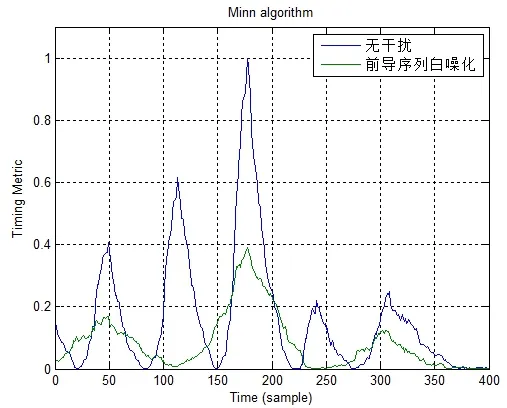
图6 Minn算法前导白噪化
由图6可知,前导白噪化后,相关函数M(d)的峰值大幅降低,在原判决器的阈值条件下,会使判决失效,但若降低判决器阈值仍然有可能搜索到M(d)峰值。
前导白噪化对Park算法的前导序列进行干扰,如图7所示:
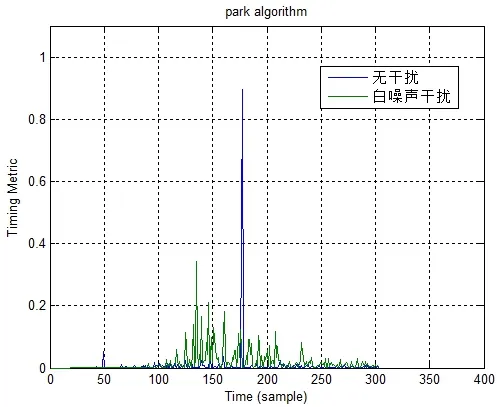
图7 Park算法前导白噪化
由图7同样可得,相关检测M(d)峰值大幅度降低,且有一定定时偏差,所以该方法对Park算法有比较好的干扰效果。
2.2 伪前导序列时域干扰
伪前导序列是由原前导序列经过循环移位产生,该方法需要掌握原前导序列的结构以及发射信息的帧结构。根据前面的推导,得到伪前导与Minn算法的仿真结果,如图8所示:
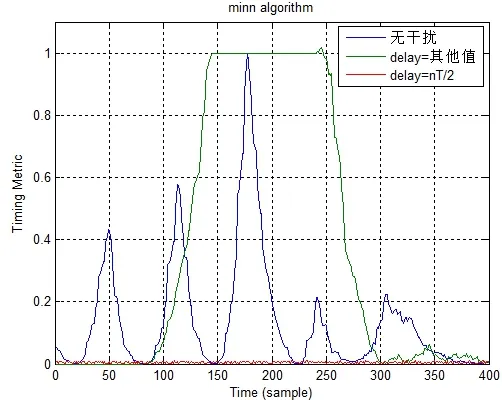
图:8 伪前导干扰Minn算法
在使用delay=nT/2时,相关函数峰值检测函数M(d)为0,dealy为其他值时得到结果出现一个平台区,与Schmidl算法结果比较吻合,符合前面的推导结果。
使用同样的伪前导序列对Park算法进行干扰,结果如图9所示:
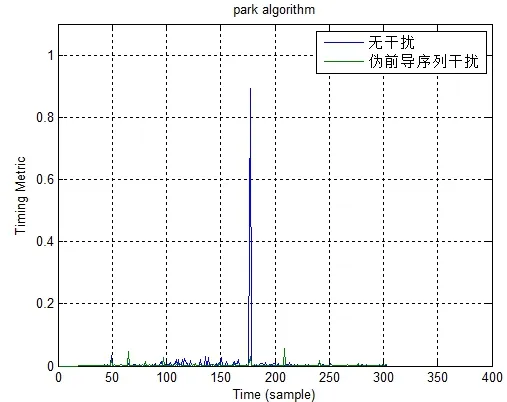
图9 伪前导干扰Park算法
Park算法受到伪前导干扰后,相关峰值检测函数M(d)输出结果与白噪声相符,已无明显的峰值,故系统无法定时。
2.3 前导序列消除
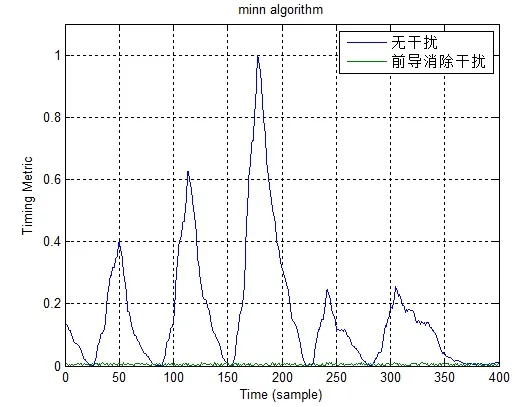
图10 前导消除干扰Minn算法
对Minn算法的干扰,前导消除后,则M(d)的分子为0,故整个M(d)函数的幅值几乎为0,效果与前面的推导一致,M(d)无明显峰值。
对于Park算法,如图11所示:
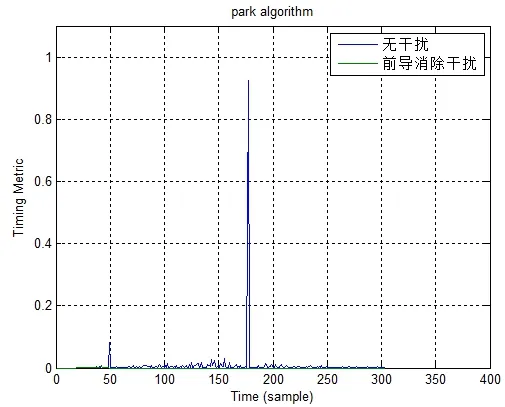
图11 前导消除干扰Park算法
对于Park算法的干扰,前导消除后,则M(d)的分子为0,故整个M(d)函数的幅值几乎为0,仿真结果也符合之前理论推导的结论。
根据以上对Minn算法和Park算法的仿真结果可以看出,前导消除干扰获得的干扰效果最佳,但要求条件较为严格,故在实际应用实现的难度较大。而伪前导序列干扰对Minn算法的效果仅仅是增加了一段误差区间,结果与Schmidl算法一致,而伪前导序列干扰对于Park算法效果较好。前导序列白噪化则是对Minn算法和Park算法都有干扰效果且需要的条件最少。从以上讨论中可知,对与Minn算法,采用前导序列白噪化干扰,对于Park算法,采用伪前导序列干扰。
3 总结
本文针对OFDM的两种同步算法采用了3种时域干扰方法进行研究,通过仿真结果确定出对于Minn算法和Park算法的最佳干扰方案。Minn和Park两种算法都是基于序列的自相关定时估计算法,这类算法提高了带宽利用率和数据传输的效率,而抗干扰性相对于基于本地序列的互相关算法来说有所降低。故未来的研究趋势也是向抗干扰性能更强的同步算法进行干扰研究。
[1] 陈西宏,胡茂凯,孙际哲,等.多径衰落信道下多音干扰OFDM系统性能分析[J].北京理工大学学报.2014,34(1):84-87.
[2] 单超,王娜,王萍. OFDM系统的抗干扰性能研究[J].系统仿真学报,2006,18(6):1618-1622.
[3] T. Clancy, Ef fi cient OFDM Denial: Pilot Jamming and Pilot Nulling[M],IEEE International Conference on Communications (ICC),2011,6.
[4] 解思瑞,黄开枝.OFDM/OFDMA 系统的导频干扰方案[J].计算机应用研究,2012,29(8):3131-3136.
[5] Matthew J. La Pan Jamming Attacks Against OFDM Timing Synchronization and Signal Acquisition[C],MILITARY COMMUNICATIONS CONFERENCE, 2012- MILCOM 2012:1-7.
[6] 常英琳.通信对抗中高效方法研究[D].西安:西安电子科技大学,2010,1:13-35.
[7] APURVA N MODY,GORDON L.Synchronization for MIMO-OFDM systerm [C].Global Telecommunications Conference,2001. GLOBECOM'01. IEEE,2001:509-513.
[8] Kleider J. Gifford S. Maalouli G, Chuprun S. Sadler B. Synchronization for RF Carrier Frequency Hopped OFDM: Analysis and Simulation [M].IEEE Military Communications Conference (MILCOM),2003,10.
[9] Huarong Zheng, Jue Tang, Bo Shen. Low-complexity joint synchronization of symbol timing and carrier frequency for OFDM systems[J]. IEEE Transactions on Consumer Electronics,2005,51(3):783-789.
[10] B. Park, H. Cheon, E. Ko, C. Kang, and D. Hong, A blind OFDM synchronization algorithm based on cyclic correlation[J].IEEE Signal Process. Lett., 2004,11(2):83-85.
[11] 魏子恒.OFDM无线通信系统中的同步研究[D].广州:华南理工大学,2010,5:6-35.
TN914
A
2015.12.23)
1007-757X(2015)06-0001-04
张 昊(1989-),男(汉族),绵阳市人,四川大学,电子信息学院,硕士研究生,研究方向:移动通信的新型干扰技术,成都,610004
夏文龙(1976-),男(汉族),成都市人,四川大学,电子信息学院,讲师,博士,研究方向:无线通信与通信对抗,成都,610004
郭庆功(1968-),男(汉族),青岛市人,四川大学,电子信息学院,教授,硕士研究生导师,研究方向:微波系统工程,成都,610004

