一类可解完备李代数

白瑞蒲，陈双双，王伟东，程荣

（河北大学 数学与信息科学学院，河北 保定 071002）

1 预备知识

幂零李代数、可解李代数是2类非常重要的李代数［1］，并在很多领域有着广泛的应用.任意一个李代数具有一个极大的可解理想与幂零理想，分别称为李代数的可解根基与幂零根基.可解根基为零的李代数，为半单李代数.在复数域上的半单李代数已经得到了较完善的结构理论.因此，可解李代数与幂零李代数是李代数结构理论研究中的重要对象，且其研究结果备受关注［2－5］.完备李代数［6－8］是一类中心为零，所有导子都是内导子的李代数.完备李代数在对称空间上有着重要的应用.本文主要研究一类以特殊的幂零李代数，以Filiform 李代数为幂零根基的可解李代数L，通过其内导子李代数adL、导子代数DerL 的结构研究，证明此类可解李代数是完备李代数，且还讨论了adLN 与adN的结构.假定所讨论的李代数是复数域上的有限维李代数.首先介绍要用到的几个概念.

设L 是域K 上的李代数［1］.如果L 的线性变换D：L→L 满足：D［x，y］＝［Dx，y］＋［x，Dy］，∀x，y∈L，则称D 是L 的一个导子.L 的导子全体记为DerL，是线性李代数.对任意x∈L，ad（x）：L→L，ad（x）（y）＝［x，y］，∀y∈L，称为内导子，ad x 全体记为ad L 称为L 的内导子李代数，内导子李代数ad L 是导子代数DerL 的理想.

如果李代数L 的中心是零，且导子都是内导子，则称其为完备李代数.

设L 是m－维幂零李代数，如果L 具有性质dimLi＝m－i－2，则称L 是Filiform 李代数.

设N 是满足如下条件的m－维的Filiform 李代数.根据乘法表直接计算可得幂零李代数N 的内导子代数ad N 的一组基为

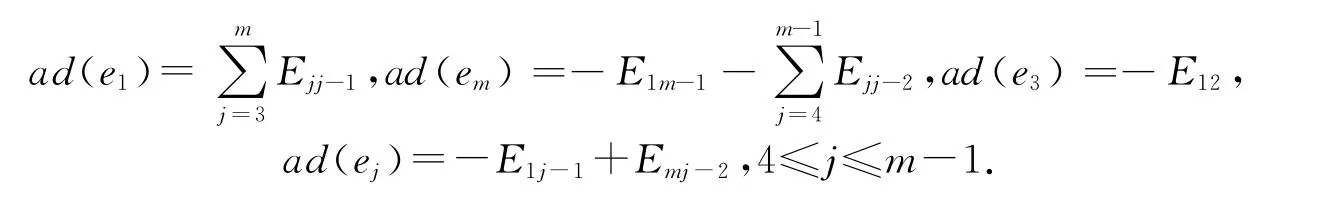
N 的内导子李代数的维数为m－1，dimad N＝m－1＜dim N＝m.

在文献［8］中，利用李代数与3－李代数［3］的结构关系证明了以N 为幂零根基的可解李代数仅有一类.

引理1［8］设L 是（m＋k）－维的以N 为幂零根基的可解李代数（k＞0），则一定有k＝1.且在同构的意义下，有且仅有如下一类：

其中3≤i≤m，4≤j≤m－1，2≤k≤m，｛e1，…，em，em＋1｝是L 的一组基.

2 主要结论

首先研究引理1中李代数L 的内导子代数与导子代数.对L 的任意一个导子D：L→L，设D（ei）＝，即D 在基｛e1，…，em，em＋1｝下的矩阵形式为，其中Eij为（m＋1）×（m＋1）－阶矩阵单位，即第i行第j 列的元素为1，其余元素为0的（m＋1）×（m＋1）－矩阵.

定理1 设L 是引理1中（m＋1）－维的以N 为幂零根基的可解李代数，且在一组基｛e1，…，em，em＋1｝下的乘法表为式（1），则dimad L＝m＋1，L 的内导子代数为

所以L 同构于L 的内导子李代数ad L.

证明：首先由乘法表（1）直接计算可得对4≤i≤m－1（省略计算过程），

由上述计算可知｛ad（e1），ad（e2），…，ad（em＋1）｝线性无关，所以得到｛ad（e1），ad（e2），L，ad（em＋1）｝是内导子代数的一组基.ad：L→ad L 是代数同构.证得L 同构于L 的内导子ad L.证毕.

定理2 设L 是引理1中（m＋1）－维的以N 为幂零根基的可解李代数，在一组基｛e1，L，em，em＋1｝下的乘法表（1），则L 的任意一个导子D：L→L 在基｛e1，…，em，em＋1｝下的矩阵为

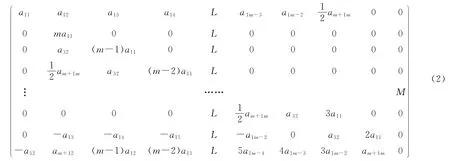
所以，导子代数等于L 的内导子李代数，即 Der L＝ad L.

对任意4≤j≤m－1，

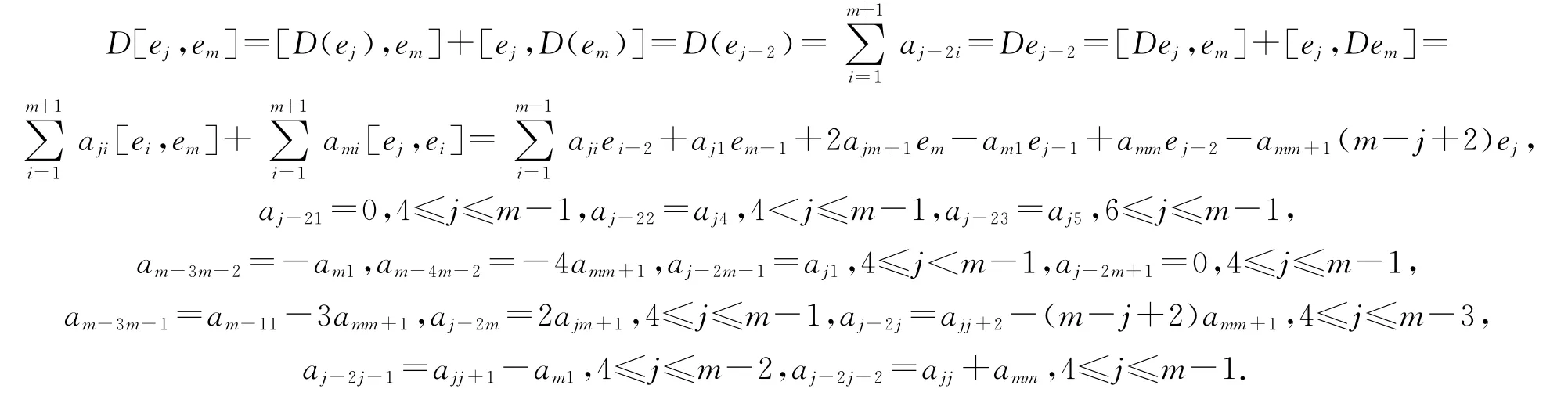
对任意2≤k≤m，

得到a1j＝－am＋1j＋1＋（m－j＋2）a1j，2≤j≤m－1.am＋1m＋1＝0，a1m＋1＝0，a1m＝0，

总结上述结论得到

所以导子在基｛e1，…，em，em＋1｝下的矩阵形式为式（2），即

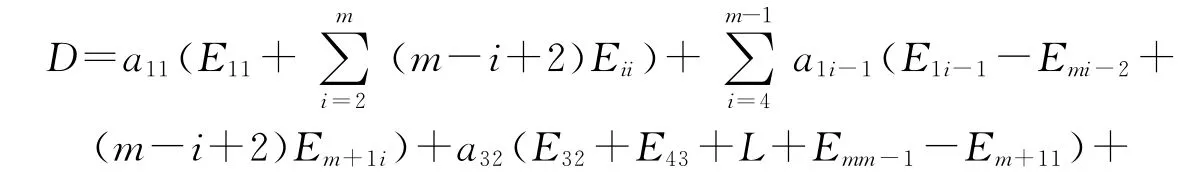
导子代数的维数为m＋1.Der L＝ad L.证毕.

定理3 设L 是引理1中以N 为幂零根基的（m＋1）－维可解李代数，则L 是完备李代数.

证明：由定理1和定理2可知，Der L＝ad L.为证明L 是完备李代数，下面证明L 的中心为零.因为L 以N 为幂零根基，所以如果z是中心元，一定有z∈N.设，则由乘法表（1），可知［e1，z］＝得到z＝a1e1＋a2e2.再由，且m≥5，得到a1＝a2＝0，因此，z＝0.证得L 是完备李代数.证毕.

定理4 设L 是以N 为幂零根基的（m＋1）－维可解李代数，则ad L 由｛ad（e1），ad（e2），L，ad（em）｝张成的子代数是 与N 同 构 的Filliform 李 代 数，且 是Der L 的 幂 零根基.

证明：由定理3可知，L 的内导子李代数同构于L，L 的幂零根基N ＝Fe1＋…＋Fem同构于导子李代数Der L 的幂零根基Der L 的幂零根基为可得结论.证毕.

由定理4可知，李代数L 的一些内导子构成的李代数adLN 与L 的幂零根基N 同构.但是，Filiform李代数N 的内导子李代数ad N 与N 不同构.因此，adLN 与adNN＝ad N 不同构.

［1］ HUMPHREYS J E.Introduction to Lie algebras and representation theory［M］.New York：Springer－Verlag，1972.

［2］ GOZE M，YU K.Nilpotent Lie algebras［M］.London：Kluwer Academic Publishier，1996.

［3］ 白瑞蒲，周恒，李佳倩.矩阵构成的3－李代数的结构［J］.河北大学学报：自然科学版，2012，32（5）：449－452.BAI Ruipu，ZHOU Heng，LI Jiaqian.Structures of 3－Lie algebras constructed by matrices［J］.Journal of Hebei University：Natural Science Edition，2012，32（5）：449－452.

［4］ 白瑞蒲，陈双双，程荣，等.具有1－维导代数的6－维3－李代数的结构［J］.黑龙江大学自然科学学报，2013，30（4）：421－424.BAI Ruipu，CHEN Shuangshuang，CHENG Rong，et al.Structures of six－Dim 3－Lie algebras with one－Dim derived algebras［J］.Journal of Natural Science of Heilongjiang University［J］.2013，30（4）：421－424.

［5］ 白瑞蒲，李奇勇，王伟东，等.素域Fp上的3－李代数［J］.河北大学学报：自然科学报，2013，33（5）：1－4.BAI Ruipu，LI Qiyong，WANG Weidong，et al.Structures of 3－Lie algebras over a prime field［J］.Journal of Hebei University：Natural Science Edition，2013，33（5）：1－4.

［6］ MENG Daoji.Some results on complete Lie algebras［J］.Comm Algebra，1994，22：5457－5507.

［7］ MENG Daoji，ZHU Linsheng，JIANG Cuibo.Complete Lie algebra［M］.Beijing：Beijing Science Press，2001.

［8］ BAI Ruipu，SHEN Caihong，ZHANG Yaozhong.Solvable 3－Lie algebras with an ideal N［J］.Electronic Journal of Linear Algebra，2010，21：43－62.