基于灰色多元线性回归的纺机行业订单预测

杨志杰，郭顺生，郭 钧

(武汉理工大学机电工程学院，湖北武汉430070)

在国际化和市场化条件下，客户需求成为企业生产的核心，严格按照订单生产成为纺机企业的主要生产方式。对订单数量的准确预测可以帮助纺机企业快速地根据订单情况改进企业的生产活动，合理分配产能，降低安全库存，进而压缩生产成本，提高利润。因此，对订单的准确预测对于纺机企业把握商机，提升企业市场竞争力有着极为重要的意义。订单预测方法很多，如神经网络预测、趋势预测和时间序列预测等。神经网络预测对数据样本的要求较高，预测稳定性一般;趋势预测和时间序列预测对外界因素的影响较为敏感，外界变化较大时，容易产生较大的偏差。灰色预测理论可在信息不充分且不确定的系统中，使用少量数据做出较准确的预测。但灰色预测模型主要针对单因素，对于多因素共同变化的现实社会适应性不强［1－3］。针对纺机企业订单易受多种因素影响的情况，基于灰色预测理论，使用多元线性回归方法对灰色预测模型进行检测和修正，得到改进后的灰色多元线性回归组合模型，该模型减弱了原始数据随机波动造成的干扰，并结合影响订单数量的多个因子共同完成订单预测。笔者检验国内某大型纺机制造企业的订单数据，结果表明，其预测的准确性和可靠性有显著提高。

1 灰色预测GM(1，1)模型

邓聚龙于1982年提出的灰色预测理论［4］，针对已知数据少、信息不足的系统，通过对部分已知信息的提取和开发，能够进行较为精确地预测，具有所需样本少、运算简便和易于检验等特点［5－6］。构建灰色预测GM(1，1)模型方法如下:

(3)生成X(1)的紧邻均值序列其中，

则灰色预测GM(1，1)模型为:

其白化方程为一阶微分方程:

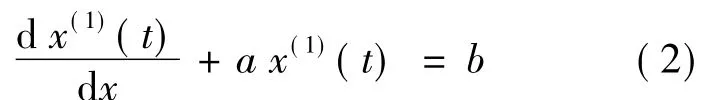
由最小二乘法可知，参数a和b满足:

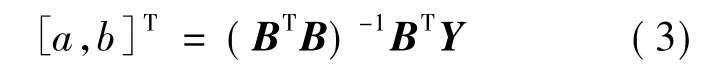
(4)求解式(1)可得:

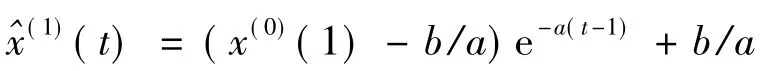
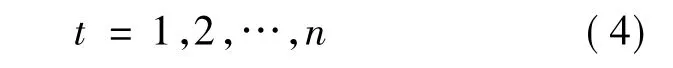
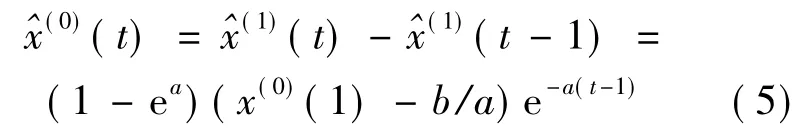
其中，t=1，2，…，n。

2 多元线性回归预测

多元回归分析是以多个原始变量为出发点，通过对数据结构进行分析，建立起原始变量与因变量间的关系并进行研究的一种数理统计分析方法。根据各原始变量的相关关系，即可建立多元线性回归方程进行预测［7－9］。

假设因变量Y与原始变量x1，x2，…，xn之间有显著的线性相关关系，即:

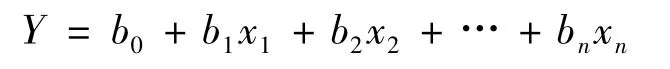
其中:bi为相关系数，i=0，1，…，n;xj为选取的原始变量，j=1，2，…，n;n为原始变量个数。

检测多元线性回归模型的方法如下:

(1)拟合优度检验(判定系数R2检验)。多元线性回归方程的拟合程度需通过判定系数R2的值进行检验，其计算公式为:

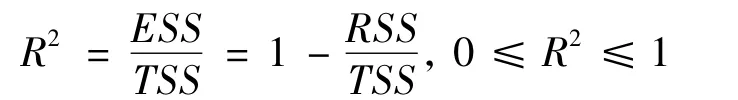
其中:ESS为回归平方和;RSS为残差平方和;TSS为总离差平方和。R2的值越接近1，表明多元线性回归模型的因变量 Y与原始变量xj间的相关程度越密切。

(2)参数显著性检验(t检验)。多元线性回归模型中每个原始变量对因变量的影响是否显著需通过参数显著性t检验进行确定，其计算公式为:

其中:βi为回归系数;s(βi)为标准误差。在显著水平α下，当时，即表明原始变量xj对因变量Y有显著影响;反之则表明影响不显著，应剔除该原始变量。

(3)多元线性回归方程的显著性检验(F检验)。因变量Y与原始变量xj在多元线性回归模型中的线性关系是否显著，可通过统计量F进行检验，分别建立如下假设H0和H1:

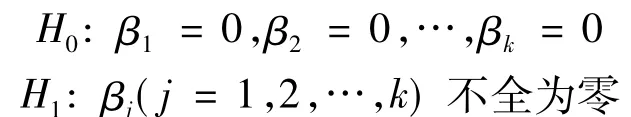
统计量F的计算公式为:

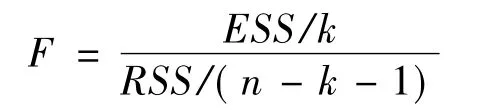
在显著水平 α 下，若F ＞Fα(k，n－k－1)，拒绝假设H0，即回归方程显著成立，反之则视为回归方程无显著意义。

3 灰色多元线性回归组合模型及其应用

纺机制造企业需要严格依据订单进行生产。首先，纺机品类繁多，一个纺机企业生产的机型可能涉及数十个种类，且客户对每台纺机的需求也可能不同。其次，纺机工艺复杂，零部件种类多，订单的生产数量小且生产周期长，并且市场对纺织品的需求趋势改变迅速，导致纺机订单时常变更。由于纺机行业的订单极易受到多种因素的影响，因此必须改善很多预测方法只选取订单作为研究对象的不足，选取多个作用于订单结果的影响因子，采用建立灰色多元线性回归组合模型的方法进行预测。根据纺机企业产品开发设计制造的特点，纺机订单预测以季度为时间节点，流程如图1所示。

图1 纺机订单预测流程图

(1)建立灰色多元线性回归组合模型:

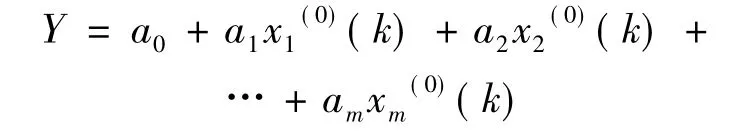
(2)根据原始数据利用灰色预测GM(1，1)方法计算出原始的灰色预测值 ^xi(0)(k)(i=1，2，…，m)，然后根据预测值计算出组合模型的回归系数 ai(i=1，2，…，m)，并进行检验，最后由得出的组合模型回归系数计算出Y值，进行预测。

(3)为了验证组合模型的准确性，笔者选取国内某排名前十的纺机企业进行验证，该企业是国家级重点高新技术企业，具有行业代表性。笔者选取2011—2012年LMV353E刷花机订单作为验证对象，调取订单数据，其数据原始值如表1所示，以成交价、订单修改数为影响因子，以季度为时间节点分析数据。

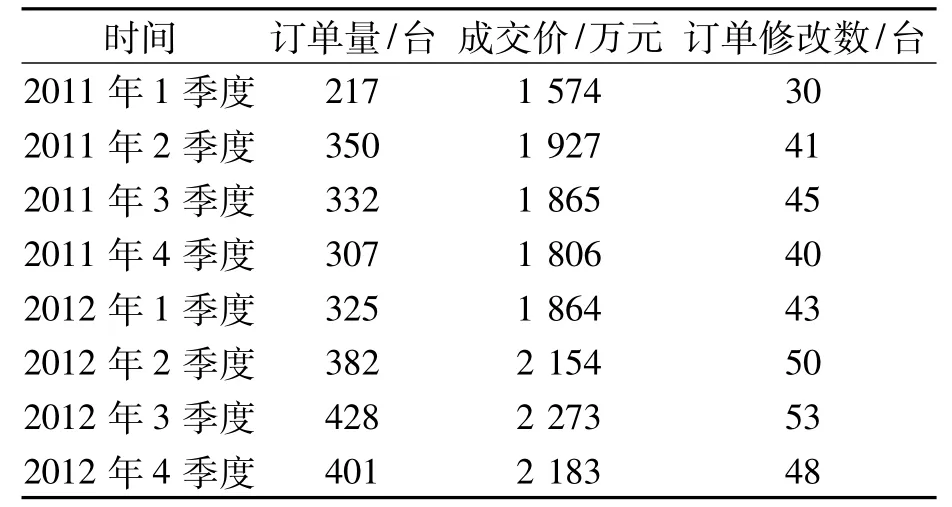
表1 某纺机企业LMV353E刷花机订单预测数据原始值

运用灰色预测软件，对企业各季度的原始数据进行加工，其界面图如图2所示，得到表2中的预测值。

图2 灰色预测GM(1，1)模型计算界面图

利用表2中的灰色预测值，运用excel 2010进行多元线性回归修正计算，其界面图如图3所示。

由图3得组合模型方程为Y=－101.46+0.059 96x1+7.469 383x2，对组合模型进行检验，R2=0.999976，线性方程拟合度高，当显著性水平 α =0.05，|t|＞ t0.025，F ＞ F0.05时，灰色多元线性回归组合模型成立。将2013年各季度数据代入组合模型，得到组合模型的预测结果，其与传统多元线性回归模型预测值的对比如表3所示。

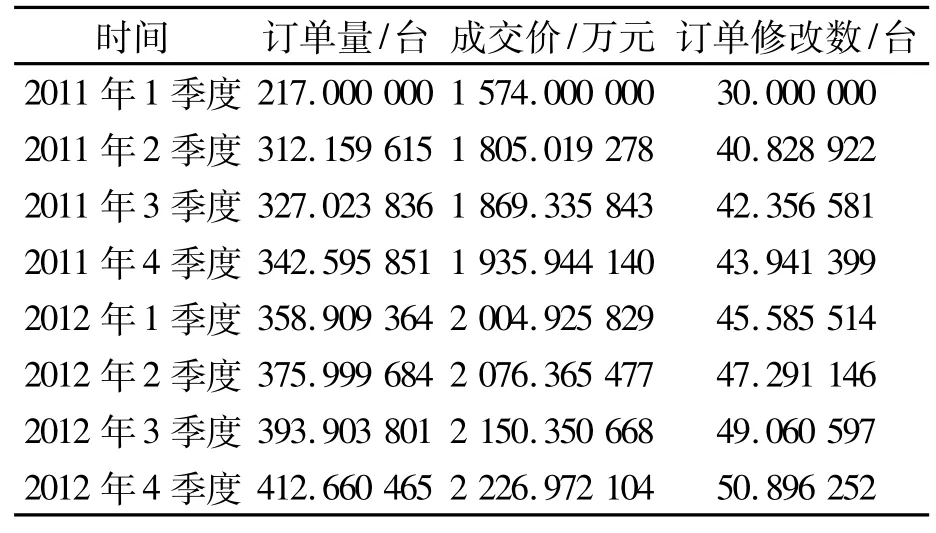
表2 某纺机企业LMV353E刷花机各数据灰色GM(1，1)模型预测值

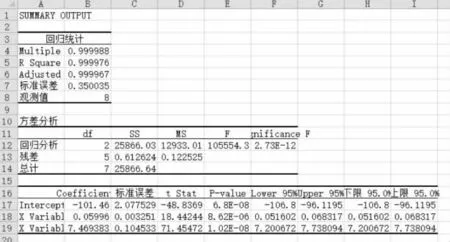
图3 多元线性回归修正计算界面图

由表3可知，误差［2］明显小于误差［1］，表明运用灰色多元线性回归组合模型进行预测的准确性相对于单一模型得到了显著提高。

表3 某纺机企业LMV353E刷花机订单预测值

4 结论

提出了基于灰色多元线性回归组合模型的纺机行业订单预测方法。利用多元线性回归的方法改善了灰色预测模型主要集中于单因素的不足，降低了原始数据随机波动对预测结果的影响，适应了纺机行业订单结果易受多因素共同作用的情况，计算简便、预测准确，可以为企业产品生产提供有力的决策依据。

［1］李西兴，徐增师.基于GM(1，1)－Markov链模型的汽车企业订单预测［J］.武汉理工大学学报:信息与管理工程版，2013，35(4):580 －582.

［2］王宏.改进的 GM(1，1)模型及其预测精度分析［J］.统计与决策，2008(23):36 －38.

［3］王重彬，李益兵.基于改进粒子群和神经网络的订单预测研究［J］.机械工程师，2013(5):137－139.

［4］DENG JL.Control problem of grey systems［J］.System Control Letter，1982，1(5):25 －32.

［5］刘思峰，党耀国，方志耕.灰色系统理论及其应用［M］.北京:科学出版社，2004:43－98.

［6］何霞，刘卫锋.灰色GM(1，1)模型的改进及应用［J］.江南大学学报:自然科学版，2011，3(3):233 －236.

［7］宋彩平，韩飞.货运量影响因素分析:多元线性回归分析［J］.现代商贸工业，2009，21(6):29 －30.

［8］黄邦菊，林俊松，郑潇雨，等.基于多元线性回归分析的民用运输机场旅客吞吐量预测［J］.数学的实践与认识，2013，43(4):172 －178.

［9］高勇华.基于商誉与多元线性回归的利润预测模型［J］.商场现代化，2007(25):65 －68.