一种用于服务质量预测的混合协同过滤方法

苏 凯，马良荔，刘 霞，郭晓明

(1.海军工程大学装备经济管理系，湖北武汉430033;2.海军工程大学计算机工程系，湖北武汉430033;3.海军工程大学 训练部，湖北 武汉430033)

在Web服务组合流程构建过程中，需要为流程中的各个功能结点选择相应的实体Web服务。随着面向服务计算技术的发展，网络上出现了大量功能相似但服务质量(QoS)各异的服务，QoS逐渐成为Web服务的主要评价指标和服务选择的重要依据［1－3］。在 QoS感知的服务选择中，用户可能对大部分候选服务都未使用过，无法掌握其QoS，而对其进行逐一调用以获取其QoS又将耗费大量资源，因而需要采取某种策略对未使用过服务的QoS进行预测。若服务组合流程选择了QoS较低但被高估的Web服务进行绑定，可能导致组合流程不满足用户需求甚至运行失败;而QoS较高但被低估的Web服务则可能在服务选择中被忽略，从而导致服务流程的整体质量下降。因此，在服务选择前对候选服务的QoS进行准确的预测是获取高质量服务组合流程的基础。

QoS属性可分为独立于用户和依赖于用户两类。独立于用户的QoS属性(如费用)值不依赖于特定的用户，不同的用户获取的QoS值相同;而依赖于用户的QoS属性(如响应时间、可靠性和吞吐量等)则可能因不同用户的网络状况、异构环境和地理位置等差异导致值变化较大［4］。传统的统计平均预测方法为不同用户提供相同的预测值，该预测值通过对服务的历史QoS数据进行算术平均得到［5－6］，未考虑不同用户的QoS感受差异性，导致预测结果准确率较低。SHAO等借鉴电子商务领域的协同过滤推荐技术，提出了一种基于协同过滤的QoS预测方法［7］，其基本假设是对某些服务拥有相似QoS感受的用户，对其他服务的感受也会比较接近。该方法采用相似用户的QoS历史信息对用户未使用过服务的QoS进行预测，在一定程度上考虑了用户的个性化差异，预测结果较统计平均法更为准确。ZHENG等提出了一种混合协同过滤方法WSRec［8］，其在对QoS进行预测时综合了基于用户和基于服务的协同过滤结果，使得QoS信息矩阵中的数据得到更充分的利用。实际上，大部分用户只使用过少量服务，因此QoS信息矩阵是极度稀疏的。

上述方法都未考虑到当QoS信息矩阵极度稀疏时，采用传统的协同过滤方法得到的预测结果可能并不准确的问题。针对该问题，笔者提出一种混合协同过滤方法，该方法可有效提高QoS预测准确度。

1 问题描述

QoS是描述服务质量的一系列非功能属性的集合，主要包括服务的价格、响应时间、吞吐量、可靠性和可用性等信息。由于传统的UDDI架构不支持服务的QoS属性信息的注册和存储，ZHOU等提出了一种可扩展的UDDI系统UX［9］，以提供对服务QoS信息的注册功能。为保证不失一般性，笔者以响应时间和吞吐量为例，讨论QoS的预测问题。

表1给出了存储在扩展的UDDI系统中的QoS数据，其中S表示服务，U表示用户，表格中的数据项表示用户调用服务感受到的响应时间和吞吐量QoS值。当数据项为φ时，以表1中U5对应S2的数据项为例，则表示用户U5未使用过服务S2，因此用户U5在调用服务 S2前需对其QoS进行预测。

表1 QoS信息存储范例

目前大多采用统计平均法，即在预测U5调用S2的QoS值时，采用S2的历史使用信息进行统计平均得到，即响应时间为(0.23+0.37+0.30)/3=0.30 s，吞吐量为(17.54+10.93+17.70)/3=15.39 kb/s。统计平均法计算简单，但是由于没有考虑不同用户处于不同的网络状况、异构环境和地理位置下，对相同服务感受到的QoS差异性，其预测精度不高。

2 混合协同过滤预测方法

2.1 定义

便于问题分析，作如下定义:

定义 1 用户集 U={U1，U2，…，Um}，Ui(1≤i≤m)表示用户集中的第i个用户。

定义2 服务集 S={S1，S2，…，Sn}，Sj(1≤j≤n)表示服务集中的第j个服务。

定义3 用户－服务QoS矩阵为:

其中:Rij= ＜ rtij，tpij＞ (1≤i≤m，1≤j≤n);rtij为用户Ui感受到服务Sj的响应时间;tpij为用户Ui感受到服务Sj的吞吐量。则QoS预测的目标为利用R中已有数据对其缺失项进行预测。

2.2 数据预处理

使用协同过滤法对用户－服务矩阵中的缺失值进行预测前，需对矩阵中的数据项进行预处理。具体方法是将用户－服务矩阵按照QoS属性分离为若干个矩阵，然后对分离后的QoS矩阵的缺失项逐一进行预测。将用户－服务矩阵R分离为响应时间矩阵RT和吞吐量矩阵TP，如式(1)所示。

2.3 相似度挖掘

常用的相似度度量方法有皮尔逊相关系数法、余弦相似法、修正余弦相似法和欧氏距离法等。其中皮尔逊相关系数法因具有易于实现和精度高等特点，被广泛应用于各类推荐系统。采用皮尔逊相关系数法计算服务a和服务b的相似度由式(2)表示。

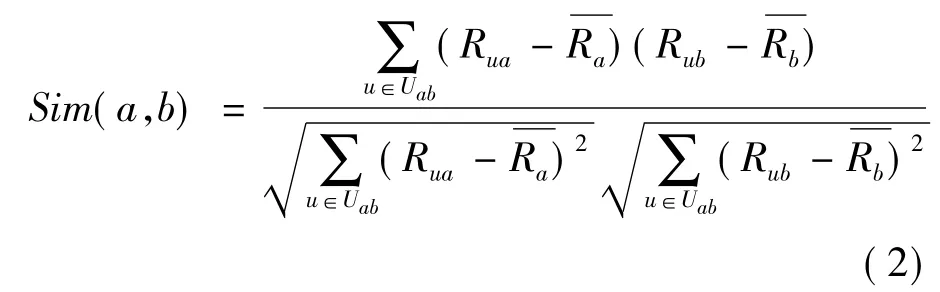
式中:Sim(a，b)为服务a和服务 b 的相似度，取值范围为［－1，1］，其值越大说明越相似;Uab=Ua∩Ub为使用过服务a和服务b的用户集合;Rua为用户u感受到服务a的QoS值;为用户集U中用户感受到服务a的QoS平均值。

由式(2)可知，皮尔逊相关系数法使用服务之间的共同用户集进行相似度计算，其未考虑两种极端情况:

(1)当两个服务不存在共同用户时，无法由式(2)得到相似度的有效值。

(2)式(2)中的分母为零的情况。例如令服务a和服务b的共同用户为用户u和用户v，假如此时用户u调用a和b的QoS相等，并且用户v调用a和b的QoS也相等，则式(2)的分母将取零，此时得到的相似度则为无穷大。

针对这两种极端情况，对式(2)进行改进，如式(3)所示。

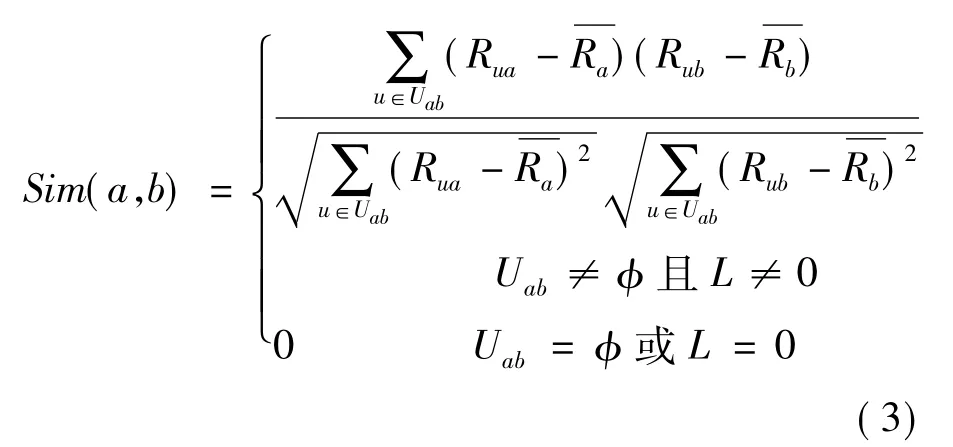
由于QoS矩阵的稀疏性，服务的共同用户通常较少，假如刚好少量的共同用户对两个服务的QoS体验较为接近，而另外一些用户对这两个服务的QoS体验差异较大，此时采用传统的皮尔逊相关系数法计算出的两个服务的相似度仍较大，这就造成了服务的相似度过量估计的问题。因此，笔者引入相似度信任因子以避免相似度的过量估计。

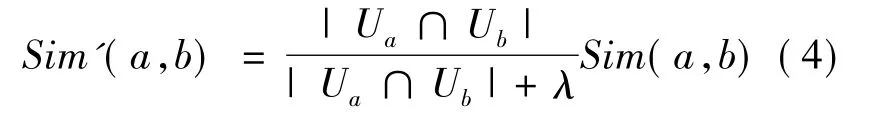
式中:|Ua∩Ub|为服务a和服务b的共同用户数;λ为预先设定的阈值，与系统中的用户总数有关。经上述相似度修正后，得到的服务相似度更为可靠。经过上述相似度计算后，将与服务a相似度最高的k个服务组成一个集合T(a)，称为服务a的top－k近邻服务集。

2.4 缺失值预测

传统的基于服务的协同过滤法使用top－k近邻集中的数据对缺失值进行预测，如式(5)所示。

式中:Rua为用户u对服务a的QoS预测值;为目标服务a对于用户集U中用户的QoS平均值;为近邻服务b对于用户集U中用户的QoS平均值。

随着网络上Web服务数的激增，大部分用户只使用过少量服务，导致QoS数据极度稀疏。因此服务的top－k近邻集中的QoS值大部分为空，即式(5)中的Rub以高概率等于零，此时仍然采用式(5)得到的预测值并不准确。因此，笔者对传统的基于服务的协同过滤公式进行改进，以提高数据稀疏条件下的预测准确度，如式(6)所示。

此外，经式(6)计算得到的预测值，存在部分值为负值的现象，而QoS属性(如响应时间、吞吐量和可靠性等)值通常为非负。笔者采用服务的QoS统计平均值代替该部分负值。

3 实验结果及讨论

由于QoS是用户在服务选择过程中的重要指标，因此QoS预测的准确性直接影响了用户服务选择方案的质量，进而影响最终服务组合流程的可靠性。因此采用网络上真实的Web服务的QoS数据集WSDREAM对笔者所述方法的QoS预测准确性进行验证，并与现有文献的其他3种算法进行对比。WSDREAM使用分布在30多个不同国家的339个用户对分布在73个国家的5 825个Web服务进行调用，通过对执行过程进行监控得到服务的QoS。为便于分析，对数据集进行处理，分别获取了150×100的响应时间和吞吐量用户－服务QoS矩阵。

笔者采用归一化平均绝对误差(NMAE)对算法的QoS预测准确度进行度量，式(7)给出了NMAE的定义。

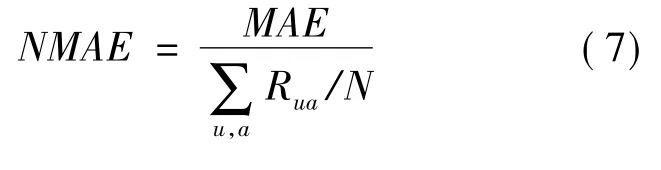
将数据集中的150个用户的QoS数据等分为10份，将其中9份轮流作为训练集，另外1份作为测试集，对预测结果进行十折交叉验证。由于现实中的Web服务QoS信息较为稀疏，因此在实验中，采用随机方式将训练集中的若干数据项移除，以提高数据集的稀疏度。对于测试集，每次验证时随机选择一个目标用户，只保留其部分数据项，然后对移除的缺失项进行预测，并采用移除项的原有值对预测结果的准确度进行评估。为更好地对算法的准确性进行估计，取10次十折交叉验证结果的均值。

3.1 不同矩阵密度下的算法准确度对比

图1和图2对比研究了笔者所提方法和其他3种算法在不同矩阵密度下的响应时间和吞吐量的预测结果。矩阵密度反映了预测系统所掌握的QoS历史信息的丰富程度。在该实验中，训练集的矩阵密度以0.01为步长从0.09递增到0.18，以研究在不同矩阵密度下的算法预测准确度。UPCC为基于用户的协同过滤法，IPCC为基于服务的协同过滤法，WSRec为文献［9］提出的混合协同过滤算法，EFMCF为笔者所提出的混合协同过滤算法。在该实验中，目标用户保留的数据项为20个，UPCC、IPCC和EFMCF的参数top－k统一取10，WSRec的参数top－k和λ分别取10和0.20，EFMCF 的参数 λ 取20。

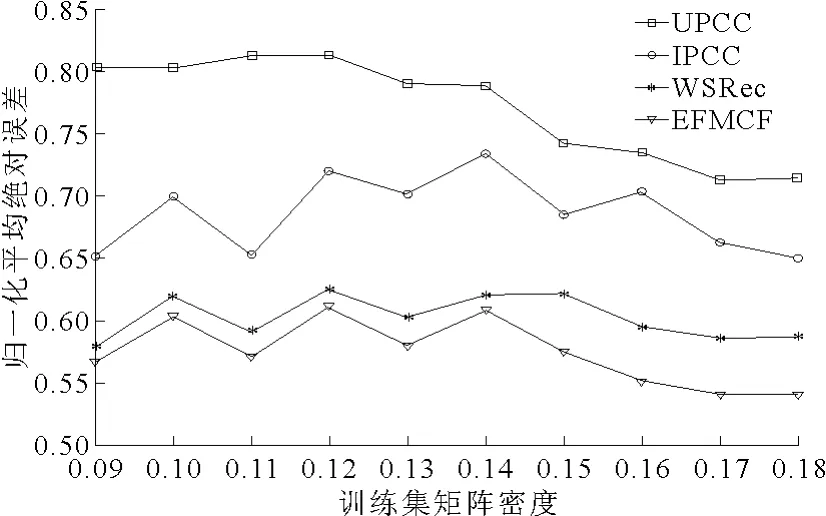
图1 不同矩阵密度下的响应时间预测结果对比

图2 不同矩阵密度下的吞吐量预测结果对比

由图1和图2可知，在不同的矩阵密度下，EFMCF的NMAE值均低于其他3种方法，表明EFMCF对响应时间和吞吐量的预测准确度更高。而IPCC的QoS预测准确度高于UPCC，因此可以认为服务之间的相似性比用户之间的相似性更为稳定。WSRec由于混合利用了QoS矩阵中的服务近邻信息和用户近邻信息，准确度得到了一定提升，但其未考虑近邻集中的大量零值问题，导致准确度提升有限。EFMCF采用基于用户的协同过滤算法对服务近邻集中的零值进行填充，进而采用基于服务的协同过滤算法得到预测值，使QoS预测的准确度得到较大提升。

3.2 不同保留项数下的算法准确度对比

图3和图4研究了目标用户取不同的保留项数时算法的响应时间和吞吐量预测结果。保留项数反映了目标用户提交给QoS预测系统服务的QoS信息的丰富程度。在该实验中，训练集矩阵密度设为0.20，保留项数以5为步长从10递增到55。

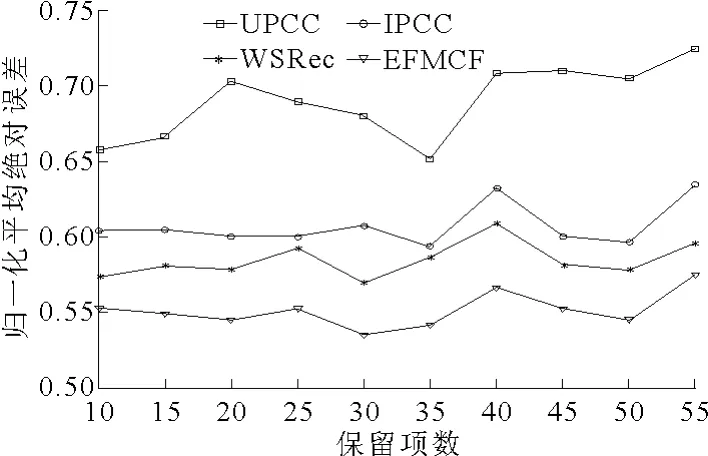
图3 不同保留项数下的响应时间预测结果对比

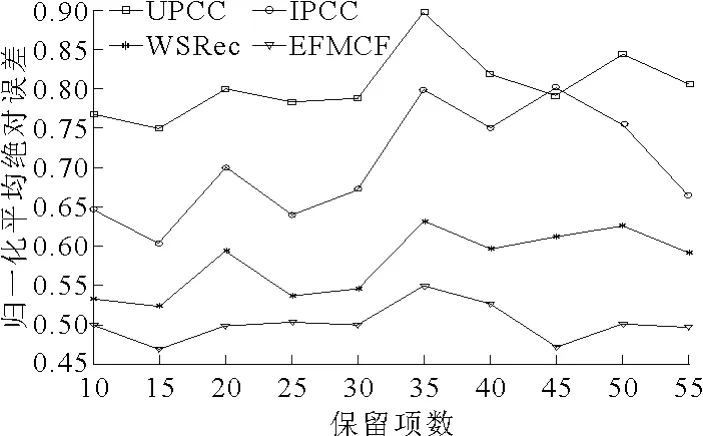
图4 不同保留项数下的吞吐量预测结果对比

由图3和图4可知，目标用户取不同的保留项数时，EFMCF对响应时间和吞吐量两种QoS的预测准确度均高于其他3种方法。说明用户只需向预测系统提供其曾经使用过服务的QoS信息，就可获得其未使用过服务的较准确QoS预测值。通过进一步的实验发现，用户提交的QoS信息越丰富，其获得的预测准确度越高，在实际应用中，该机制可鼓励用户向预测系统提供其使用过服务的QoS信息。

4 结论

针对目前QoS预测方法的不足，提出了一种混合协同过滤预测方法。采用网络上真实的Web服务QoS数据集进行实验验证，结果表明，该方法可显著提高对Web服务QoS的预测准确度。虽然该方法只考虑响应时间和吞吐量两个QoS属性，但可同时用于其他QoS属性的预测。

Web服务的QoS数据主要通过服务供应商的发布、用户使用反馈和对服务执行过程实时监控3种方式收集。笔者使用的QoS数据来源于第3种渠道，因此其数据是客观可信的。通过另外两种渠道收集的QoS信息，可能存在QoS不可信的情况，如供应商的夸大发布和用户的虚假反馈等。假如采用虚假的QoS信息进行服务选择，将严重影响服务选择结果的可靠性。

［1］SU K，MA L L，GUO X M，et al.An efficient discrete invasive weed optimization algorithm for Web services selection［J］.Journal of Software，2014，9(3):709－715.

［2］YU T，ZHANGY，LINK J.Efficientalgorithms forWeb services selection with end－to－end QoS constraints［J］.ACM Trans on theWeb，2007，1(1):1 －26.

［3］苏凯，马良荔，郭晓明，等.一种QoS感知的服务全局优化选择算法［J］.华中科技大学学报:自然科学版，2014，42(4):72 －76.

［4］ZHENG Z B，ZHANG Y L，LYU MR.Distributed QoS evaluation for real－ world Web services［C］∥IEEE International Conference on Web Services.［S.l.］:［s.n.］，2010:83 －90.

［5］XIAO R L.Constructing a novel QoSaggregatedmodel based on KBPP［J］.Communications in Computer and Information Science，2010，107(3):117 －126.

［6］ZENG L，BENATALLAH B.QoS－awaremiddleware forWeb services composition［J］.IEEE Trans on Software Engineering，2004，30(5):321 －322.

［7］SHAO L，ZHANG J，WEIY，et al.Personalize QoS prediction for Web service via collaborative filtering［C］∥IEEE International Conference on Web Services.［S.l.］:［s.n.］，2007:439 －446.

［8］ZHENG Z B，MA H，LYU MR，et al.WSRec:a collaborative filtering based Web service recommender system［C］∥IEEE International Conference on Web Services.［S.l.］:［s.n.］，2009:437 －444.

［9］ZHOUC，CHIA L T，SILVERAJAN B，etal.UX:an architecture providing QoS－aware and federated support for UDDI［C］∥Proc.of the Int’1 Conf on Web Services.Las Vegas:IEEE Computer Society，2003:171－176.