多融资企业物流金融贷款价值比及利率研究

杜 军，霍鹏美，仪婷婷

(天津大学管理与经济学部，天津300072)

中小企业融资难的问题越来越成为制约我国中小企业发展的瓶颈，而物流与金融业务的结合则能有效解决这一问题。与传统银行贷款集中在不动产抵押或第三方信誉担保的模式不同，物流金融业务中的中小企业可以将其所拥有的生产资料、存货和商品等动产作为抵押，银行依据该动产的价值或财产权利为融资企业提供其所需要的贷款。通过开展物流金融业务可以有效缓解供应链上资金流失衡问题，实现物流、信息流和资金流同步化，进一步提高供应链效率［1］。

目前以联想公司为代表的企业在实践中推出了一种新型物流金融业务。在该模式中，物流企业通过构建融资平台，在与银行签订总贷款合同的前提下同时向多家融资企业自主地提供物流金融服务，称之为集成式物流金融业务。集成式物流金融业务中，物流企业除承担传统业务外，还负责货物采购、质量审核、运输、监管、配送和代理结算整个过程，具备货物的评估和处理能力，形成一体化服务，使物流企业更加全面地嵌入到供应链中，有利于提升其核心竞争力及持续经营能力。

目前，国内外对物流金融业务进行了较多的研究。BARNETT［2］和 BIEDERMAN［3］对物流金融的现状及其发展趋势进行了相关研究。冯耕中［4］和李毅学［5］等对物流金融业务的内涵、国内外物流金融业务的异同，以及相应的风险管理进行了系统分析。李毅学［6］等研究了价格随机波动下存货质押融资业务质押率的确定方法。张媛媛［7］等从企业－银行不合作博弈的角度出发，基于零售商面临报童问题的假设，考虑质押物的处理价不高于储存费用的情况，对银行的贷款价值比进行了研究。李毅学［8］等综合考虑了外生的企业违约概率、质押存货的价格波动率、贷款的周期和盯市频率等因素的影响，定量地对贷款价值比进行了研究。

现有研究多集中在定性分析和发展较成熟的存货质押模式的定量分析，且均从银行的角度出发，忽视了物流企业在物流金融中的桥梁作用，不利于物流企业的长期发展。目前物流金融理论一般将贷款利率作为已知常量，而不是决策变量，显然不适用于当前银行贷款利率市场化的改革。因此，对集成式物流金融的研究具有重要意义。

1 多融资企业物流金融业务运作模式

集成式物流金融业务采用二级决策机制。首先由银行和物流企业签订总借款合同，银行根据物流企业的规模、信用等级和资金实力等条件，确定贷款的利率，即所谓的第一级决策。物流企业获得资金后，同时向多个融资企业提供物流金融业务，确定合适的贷款价值比以保证其收益的实现，即所谓的第二级决策。集成式物流金融业务的概念框架如图1所示。

图1 集成式物流金融的概念框架图

在集成式物流金融业务中，融资企业首先与物流企业签订协议，约定开展物流金融业务。经双方协商签订二级契约。物流企业根据融资企业对采购货物型号、品质等要求，寻找合适的供应商，签订采购合同，付款后，取得货物的所有权。融资企业依据约定金额向物流企业交纳保证金，物流企业在收取保证金后，向融资企业提供货物。集成式物流金融运作模式如图2所示。

图2 集成式物流金融运作流程图

集成式物流金融的业务环节具有区别于存货质押、保兑仓等传统物流金融业务的特点。在该业务中，物流企业代替具有相同需求的多个融资企业向上游供应商采购货物并拥有所有权，提供商务服务、物流服务和融资结算等服务。集中采购可以产生规模经济效应，物流企业在获得物流收益、融资收益之余还可获得一部分差价收入。基于风险收益对等原则，物流企业在获得收益的同时还需要承担交易风险，即当融资企业违约时，物流企业承担处理货物的跌价风险。

2 相关假设与模型描述

由上述可知，单一物流企业对多方融资企业的集成式物流金融属于二级决策机制。在第一级决策中，物流企业与银行约定贷款的期限及贷款利率。对物流企业而言，在该契约中的决策变量是贷款利率，即在同时考虑收益和风险的情况下确定有效的贷款利率范围。在第二级决策中，对物流企业而言，决策点在于如何确定最优的贷款价值比。对集成式物流金融模型建立的假设和说明如下:

(1)第一级决策中，银行对物流企业的贷款利率为r，贷款周期为t，则t时末1元贷款的本息和为 ert。

(2)货物价格为p0，其在整个物流金融周期内保持不变。

(3)对第i个融资企业而言，其货物期初的采购量为q0，假设每个融资企业的期初采购数量均相同。期末货物的需求xi是随机的，其先验的分布函数及概率密度函数分别为Fi(x)，fi(x)。

(4)物流企业提供的贷款价值比为ω，即期初的贷款额为ωp0q0;融资企业需要交纳的保证金为(1－ω)p0q0，此时融资企业可获得数量为q1的货物，q1由物流企业根据融资企业的信用级别及历史经验给出。

(5)物流企业向融资企业要求的贷款利率为R，则t时末，融资企业贷款的本息和为ωp0q0eRt，出于简化的目的，假定提供给每个融资企业的R均相同。

(6)c为物流企业提供采购、保管和物流服务所需的单位成本，c为常数。

(7)贷款期末，如果市场出现不利的变化，第i个融资企业的违约概率为hi。

(8)当期末需求小于q0时处理残值的净收入为s(s＜p0)，假定融资企业和物流企业面对同样的残值处理市场，即两者的s相同。

(9)物流企业通过控制ω和R来获得收益，即物流企业在确定ω和R时需同时考虑其融资收入、物流收入和差价收入。在二级决策中，假定R已确定，则物流企业的决策变量集中在ω。

基于以上假设，用Πi表示物流企业来源于第i个融资企业的利润，则当融资企业不违约时，Πi=ωp0q0(eRt－ert)－cq0;当融资企业违约时，Πi=xip0+s(q0－xi) －cq0－ ωp0q0ert。

化简后可得到:

3 集成式物流金融贷款价值比

在集成式物流金融业务中，区分不同融资企业的因素为违约概率和期末各融资企业所在地区的需求量。由于物流企业的风险有一部分来源于融资企业的违约风险，因此，笔者通过研究融资企业的违约概率，给出贷款价值比的范围，对物流企业控制风险具有重要意义。

假定融资企业决策的依据为利润最大化，即当市场情况出现不利变化时融资企业会做出使其利润最大的决策。当融资企业向物流企业交纳(1－ω)p0q0的保证金时，其有权从物流企业获得数量为q1(q1＜q0)的货物，用ξ表示融资企业的利润，则融资企业选择不违约时，ξ=p0min(x，q0)+s max(0，q0－x)－ωp0q0eRt;融资企业选择违约时，ξ=p0min(x，q1)+s max(0，q1－ x) － (1 －ω)p0q0。

定理1 当贷款价值比ω＜ω1时，融资企业的违约概率为0，物流企业不会面临违约风险;当ω1＜ω＜ω2时，融资企业的违约概率为F(α);当ω＞ω2时，融资企业的违约概率为1。其中:

证明过程如下:

(1)期末需求x＞q0时，选择不违约的利润选择违约的利润由不违约 ＞违约可知，当时，融资企业会在需求为x＞q时选

0择不违约。

(2)期末需求x＜q1时，选择不违约的利润选择违约的利润由不违约＞违约可知，当时，融资企业会在需求为x＜q1时选择不违约。

(3)期末需求q1＜x＜q0时，选择不违约的利润ξ=p0x+s(q0－x)－ωp0q0eRt;选择违约的利润ξ=p0q1－(1－ω)p0q0。由不违约＞违约可知，给定ω，当x＞α时，融资企业选择还款，则可得到如下结论:

由上述研究可知，物流企业来源于某一融资企业的期望利润E(Πi)满足式(1)，笔者将研究当融资企业为多方时，物流企业的期望利润如何确定的问题。假定第i个融资企业的需求函数服从均值为 μi，方差为 σi2的正态分布。F(x)，f(x)分别为考虑多个融资企业时的联合分布函数和联合概率密度函数，ω为考虑多个融资企业时的联合贷款价值比。

设xi为第 i个融资企业的需求，x=(x1，x2，…，xi)T为期末总需求，则 x=(x1，x2，…，xi)T服从均值为E(x)，协方差为∑的正态分布。其中:

E(Π)为物流企业的总利润，则:

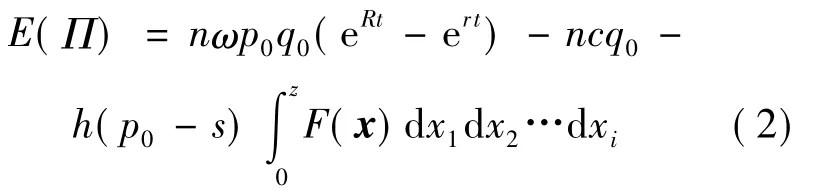
定理2 如果货物的期初单价为p0且保持不变，考虑多个融资企业时的总需求的分布函数为F(x)，则对物流企业而言的最优贷款价值比为其中:

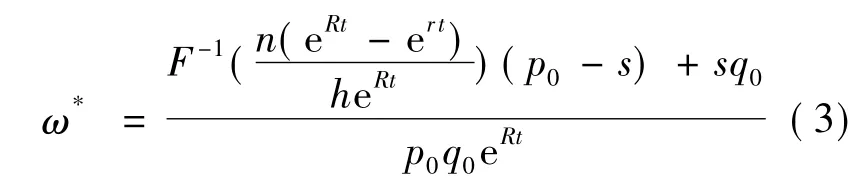
其证明过程如下:由物流企业的期望利润E(Π)对ω求导，可得:

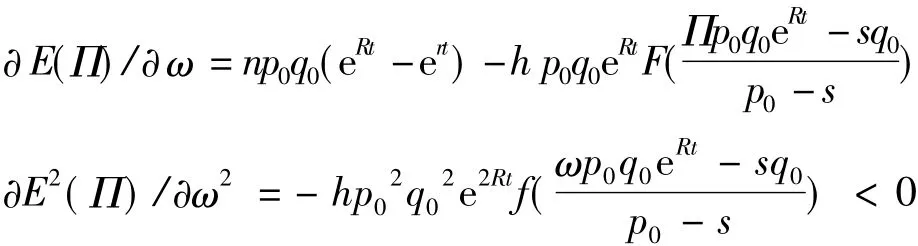
因此令∂E(Π)/∂ω =0，可得使物流企业期望利润最大的贷款价值比ω*，即:

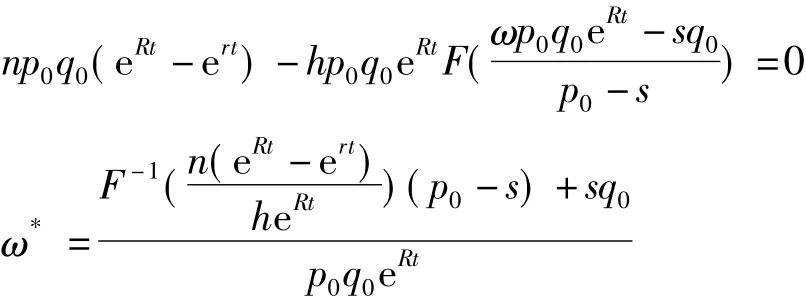
4 银行贷款利率研究

假设物流企业采用下侧风险限制来控制风险，物流企业愿意承受的最大损失为L，其为贷款额的函数，即L=nlωp0q0。物流企业愿意承担的最大风险为β，有P(loss＞L)=hP(loss＞L)≤β，即贷款损失大于L的概率等于融资企业违约和违约时物流企业的损失大于loss这两个事件同时发生时的概率。笔者的上述研究得出了物流企业的期望利润，从期望利润的表达式可知，银行的贷款利率r与物流企业的利润呈负相关。当物流企业的利润为0时对应的r即为物流企业可接受的银行贷款利率的上限。因此，有定理3成立。

定理3 在同时考虑物流企业风险和收益的情况下，可接受的银行贷款利率的有效范围为(r1，r2)。其中:

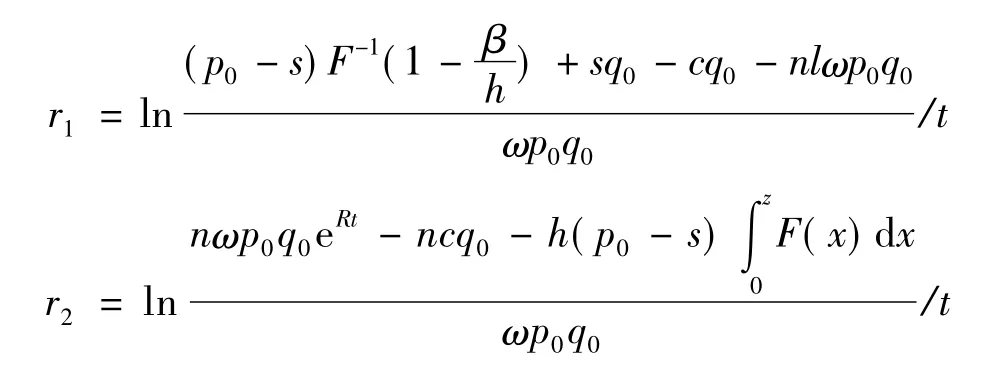
其证明过程如下:

(1)当市场出现不利变化，融资企业以h的概率违约时，物流企业的损失为loss=xp0+s(q0－x)－cq0－ωp0q0ert。考虑到物流企业的下侧风险限制，有P(loss＞L)=hP(loss＞L)=hP(xp0+s(q0－x)－cq0－ωp0q0ert＞n lωp0q0)≤β，即:

(2)当物流企业的期望利润E(Π)=nωp0q0·

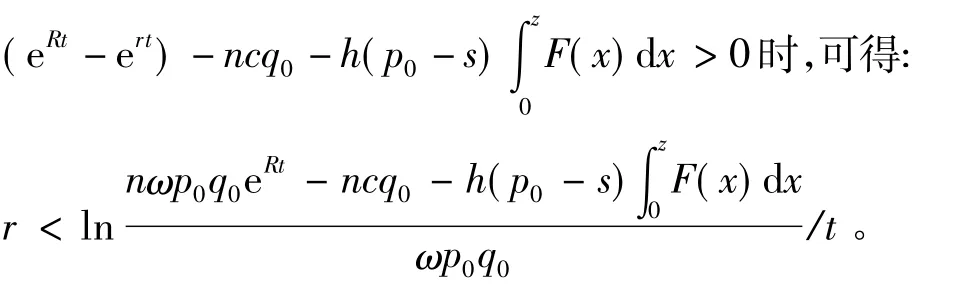
5 结论

现有对于物流金融业务的研究大多从银行角度来研究贷款价值比，笔者创造性地基于物流企业的视角研究贷款价值比。在贷款价值比研究中，给出在融资企业的需求函数存在相关性时物流企业来源于全部的融资企业的期望利润，并且推导出最优贷款价值比的数值，给出了基于利润最大化与风险控制的贷款价值比。在贷款利率研究中，基于物流企业下侧风险控制的假设，给出了有效银行贷款利率的范围。

［1］李 毅学，冯耕中，屠惠远.供应链金融创新中下侧风险规避银行的贷款额度分析［J］.系统科学与数学，2009，29(11):1552 －1668.

［2］B ARNETTW.What’s in a name:a brief overview of asset－ based lending［J］.Secured Lender，1997，53(6):80－82.

［3］B IEDERMAN D.Logistics financiers［J］.The Journal of Commerce，2004(4):40 －42.

［4］冯 耕中.物流金融业务创新模式分析［J］.预测，2007，26(1):49－52.

［4］DENG JL.Control problem of grey systems［J］.System Control Letter，1982，1(5):25 －32.

［5］刘思峰，党耀国，方志耕.灰色系统理论及其应用［M］.北京:科学出版社，2004:43－98.

［6］何霞，刘卫锋.灰色GM(1，1)模型的改进及应用［J］.江南大学学报:自然科学版，2011，3(3):233 －236.

［7］宋彩平，韩飞.货运量影响因素分析:多元线性回归分析［J］.现代商贸工业，2009，21(6):29 －30.

［8］黄邦菊，林俊松，郑潇雨，等.基于多元线性回归分析的民用运输机场旅客吞吐量预测［J］.数学的实践与认识，2013，43(4):172 －178.

［9］高勇华.基于商誉与多元线性回归的利润预测模型［J］.商场现代化，2007(25):65 －68.