13 版清单规范下工程量减少引起的综合单价调整研究*

柯洪 邹仲涛 孙永娜

(1. 天津理工大学管理学院，天津 300384;2. 中大信(北京)工程造价咨询有限公司，北京 100107)

0 引言

由于建设工程具有工期长、受客观因素影响大、复杂度高等特点［1］，工程量减少引起综合单价调整的现象普遍存在［2-4］。根据13 版清单规范规定工程量减少超过15%时综合单价应进行调整［5］，但是在实际项目中，综合单价调整仍有一些问题亟待解决，其中综合单价按照约定的单一系数进行调整，调整效果不理想［6］;综合单价调高会导致在调价临界点附近，随着工程量减少总价上升的现象产生。工程量减少引起的综合单价调整，直接关系到发承包双方的切身利益，若处理不当极易产生纠纷。因此，工程量减少引起的综合单价调整问题成为发承包双方共同关注的热点问题。

目前在国内的学术研究中，对工程量减少引起综合单价调整的研究可大致归纳为三类。孙玉红等［7］通过文献研究对引起工程量减少的原因进行了分析;严玲等［5］通过访谈的方式探讨了工程量变化时措施项目费的调整问题;陈静等［4］从合同价款状态角度出发，揭示了工程量偏差对综合单价调整的影响机理。鲜有研究者对工程量减少时综合单价调整存在的问题进行详细的研究。因此，本文将运用文献研究和案例分析的方法，对工程量减少引起综合单价调整问题进行探讨，减少发承包双方在工程结算中的纠纷，以期对发承包双方均有所裨益。

1 工程量减少引起的综合单价调整存在的问题

1.1 约定单一调价系数不合理

在工程实践中，综合单价调整通常采用比例调整法，即在原综合单价的基础上做出相应的浮动，具体的浮动比例由发承包双方在合同中约定［6］，该种方法的实质是针对工程量减少的任何值，综合单价只按一个系数进行调整。若从施工成本角度对综合单价进行分析会发现该种调整方式不严谨。从施工成本角度来看，综合单价实质是由单位固定成本、单位可变成本及利润构成，工程量减少不会影响单位可变成本［8］，但包含在减少的工程量中的固定成本摊销未能得到有效回收，进而使承包商利润受损，具体关系见图1。

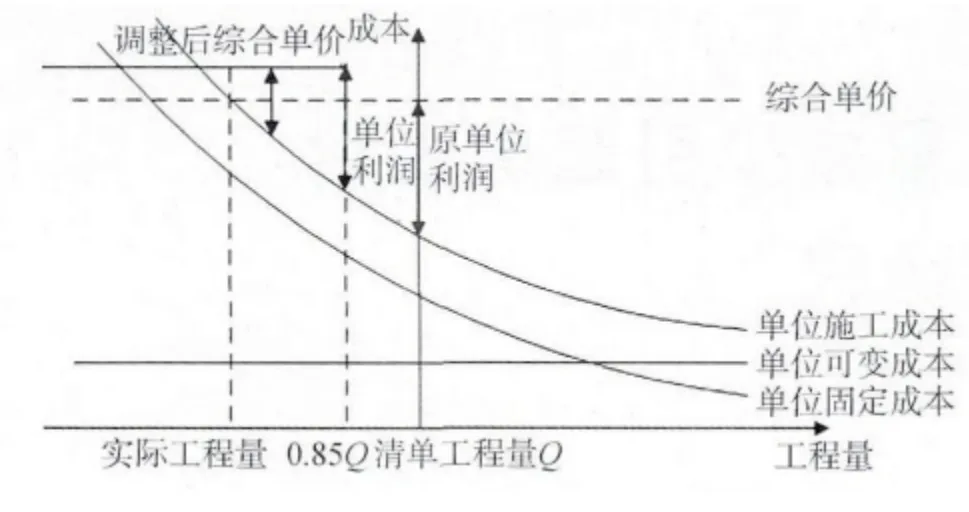
图1 综合单价与工程量的关系图

由图1 可以看出，在工程量减少的过程中单位利润不断降低，承包商若想维持原有的利润水平，则对任意工程量变化值点都必须确定一个与之相对应的综合单价。在实践中，工程量的变化值不确定，与之对应的综合单价也不确定。但是按单一系数调整后综合单价值只有一个，调整后的综合单价与实际工程量对应的综合单价可能不一致。若低于实际综合单价则承包商的利润受损，反之，承包商会获得超额利润。因此，本文认为按合同约定的单一调价系数进行综合单价调整的方式不合理。

1.2 综合单价调整存在悖论

根据调整后的综合单价得到的总价可以分为两部分，一部分是原综合单价与实际工程量的乘积，另一部分为实际工程量与调价临界点处工程量(0.85 Q0，Q0为招标工程量清单中所列工程量)之差所含的分摊费。据此分析，调整后的总价不会超过调价临界点处的总价，然而针对具体的综合单价调整事件，发承包双方进行综合单价调整时，在调价临界点0.85 Q0附近会出现工程量减少总价上升的现象，本文将该种现象界定为综合单价调整悖论。综合单价调整只是为了维持承包商原有的利润水平，并非使承包商获得超额利润，总价上升违背了综合单价调整的目的。该种现象有可能使承包商在工程量减少临界点处为了调价故意将工程量减少，进而得到更高的工程价款。本文将结合算例对该悖论进一步分析。

在某蓄水池土方工程中，清单工程量为1 000m3，采用机械挖土，投标报价中综合单价为15 元/m3，另外合同约定，工程量增减幅度超过15%时，综合单价对应的调整幅度为20%。在施工过程中因设计变更，导致工程量减少到800m3。

该算例中工程量减少20%，根据13 清单规范的规定需要进行综合单价的调整。为清晰地体现在调价临界点附近的悖论问题，本文采用非等距取值的方法计算从800 ～1 000m3的工程量所对应的总价，计算结果见图2。在调价临界点850m3处总价突增，且工程量在800 ～850m3内总价高于工程量在850 ～950m3内的总价，使承包商获得额外利润。

图2 总价与工程量关系图

上述问题的本质是目前综合单价调整的方法不合理，因此本文认为构建合理的综合单价调整方法，是解决问题的关键。

2 综合单价调整方法研究现状

2.1 综合单价调整方法综述

通过对文献［6，9］资料的整理发现，目前综合单价调整的方法大致可归纳为两大类，一类是精确计算法;另一类是比例调整法。

2.1.1 精确计算法

通过精确计算法对综合单价进行调整时有两种计算方法，一种是调增算法，即将实际工程量和原综合单价相乘，再加上调价临界点和实际工程量之间的工程量所含的分摊费;另一种是调减算法，即先计算出调价临界点处的施工总价，再将临界点处工程量与实际工程量之间的变动成本剔除，具体计算方法如下。

(1)调增算法。将管理费分为固定管理费(费率是a)和可变管理费(费率是b)，其中固定管理费是分摊费，不随工程量的变化而变化，而可变管理费随着工程量的减少而减少。合同约定工程量内的利润率为p。当Q1＜0.85Q0时，工程量减少部分 (0.85Q0－Q1)的固定管理费和利润需要在剩余工程量中得到补偿，因此，此时综合单价P1为:

式中，Q0是清单工程量;Q1是实际工程量;P0是原综合单价，文中相同字母含义相同。

当工程量变为零时意味该部分工作被取消，针对该种情况本调价公式不适合。

(2)调减算法。当Q1＜0.85Q0时，工程量减少部分 (0.85Q0－Q1)的可变成本需要在调价临界点处的总价上剔除，此时综合单价P1为:

式中，C1为(0.85Q0－Q1)中的单位变动成本。

2.1.2 比例调整法

在工作中，比例调整法通常是发承包双方采用最多的一种方法，即发承包双方在合同中约定一个调价的系数，当工程量减少超过15%时，减少后剩余工程量的综合单价在原综合单价的基础上按照调价系数进行上浮。综合单价的计算如公式(3)所示:

式中，k 为约定的调价系数。

2.2 综合单价调整方法对比分析

目前常用的综合单价调整方法主要有上述三种，为了更好地凸显各种方法的特点，现通过作表对比分析各种方法，见表1。

表1 综合单价调整方法对比分析表

根据表1 分析可知，调减算法相对调增算法的可操作性要强，计算精确度比比例调整法高。因此，调减算法是精确计算法中相对较合理的方法。

3 综合单价调整方法的建立

综合单价按单一系数调整不合理问题的实质是不能根据工程量变化范围约定不同的调整比例;调价悖论问题的本质是约定的比例幅度过高违背了综合单价的调整原则。基于上述分析，本文将通过两种思路解决综合单价调整问题，一是修正目前常用的比例调整法，即根据不同的工程量范围约定不同的调整比例;二是选择更加精确的综合单价计算方法。

3.1 基于分层思想的比例调整法

从综合单价和工程量的关系图(图1)可以看出，工程量的变化是一个动态过程，单位施工成本随工程量减少呈连续上升的趋势，从而导致承包商的单位利润受损。另外，单位施工成本是一条光滑曲线，要想保证承包商的单位利润不变，理论上要满足代表综合单价的直线变为一条在各点处与单位成本曲线斜率相同的曲线，如图3所示。若达到该种效果需要在合同中对工程量的每一个值均约定一个调整比例，而在实际工作中不具有可操作性。因此，本文认为可以将工程量划分为不同的区间，在不同的区间内约定不同的调整比例，具体思路如下。

图3 综合单价分层调整图

发承包双方可以根据工程经验或按照调减算法，计算出调节临界点附近Q1处综合单价值，然后确定一个固定值b，当工程量在Q1的基础上依次减少b 的整数倍时，综合单价在原综合单价的基础上相应调增an(其中n = 1，2，3，…)，本文以4 次调整为例画图，见图3。

根据图3 可以看出，约定的综合单价调整比例在调价临界点处最小，工程量减少的越多约定的比例越大。若发承包双方根据该思想约定调整比例，当工程量减少事件发生时，可以按照实际工程量所处的区间选择具体的调整比例。这避免了只按约定的单一系数调整综合单价不合理的现象，加之，调价临界点附近约定的调整比例更接近实际，也解决了综合单价调整悖论问题。

3.2 修正调减法

本文在2.2 节通过对比分析得知，调减算法是精确计算综合单价的一种相对准确的方法，但是该方法使用的前提是要计算综合单价中的可变成本。由于综合单价中可变成本除了包含人工费、材料费、施工机具费外，还含有一定的管理费，所以可变成本的计算难度增大，调减算法使用存在障碍。为此，本文对现有方法进行修正，如公式(4)所示。

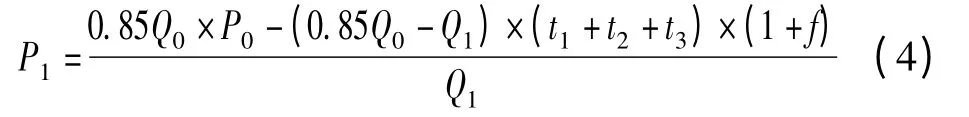
式中，t1为综合单价中人工费;t2为综合单价中的材料费;t3为综合单价中的施工机具费;f 为修正系数，可以根据管理费取费费率确定。

修正调减法是根据实际工程量重新确定综合单价，不存在调价系数不合理问题，与此同时计算结果精确度的提高也避免了调价悖论问题。

3.3 综合单价调整方法的选择

发承包双方可以根据需要选择上述两种方法，若发承包双方希望工程量减少事件发生后再对综合单价调整事项进行协商，则可以选择修正调减法。若发承包双方希望在合同签订时就对综合单价的调整进行详细的约定，以免工程量减少事件发生后产生纠纷，则可以选择基于分层思想的比例调整法。两种方法都能解决目前综合单价调整中存在的问题。

4 工程量减少引起的综合单价调整方法的应用

4.1 案例背景

某教学楼工程中标后，发包方与承包商签订了一份总承包合同。合同中约定当工程量发生变化时，按照13 版清单规范进行合同价款的调整，具体调整内容根据实际情况协商。在施工过程中，因设计变更使得有梁板的混凝土工程的工程量由原来的500 m3减少到420 m3，混凝土工程的综合单价是550 元/ m3。

4.2 案例分析

该工程签订合同中要求工程量发生变化后合同价款的调整按照13 版清单规范，即当工程量减少超过15%时，减少后剩余部分工程量的综合单价应调高。案例中工程量减少16%，按照规定必须进行综合单价的调整。合同价中混凝土有梁板工程的综合单价分析表见表2，其中管理费费率10%，利润率5%。

表2 综合单价构成分析表

根据发承包双方在合同中的约定，本案例应该选择修正调减法进行计算，具体计算步骤如下。

清单工程量Q0= 500m3;原综合单价P0=550 元;实际工程量Q1= 420m3;人工费t1=123.2 元;材料费t2= 308.7 元;施工机具费t3=23.1 元;本案例中管理费费率为10%，修正系数f 取管理费系数一般即f = 5%。

P1=［0.85 ×500 ×550－(0.85 ×500－420)×(123.2 +308.7+23.1)×(1+5%)］÷420

= 550.9(元/m3)

实 际 总 价 S = 550.9 元/m3× 420m3=231 378 元

调价临界点总价S = 550 元/m3× 425m3=233 750 元

根据计算结果可知实际总价小于调价临界点的总价，调价悖论不再存在。

5 结论

本文着重分析了综合单价的调整问题，结合众多研究者对综合单价调整方法的探讨，构建了基于分层思想的比例调整法和修正调减法，并通过具体案例对方法进行了验证分析，对工程量减少引起的综合单价调整问题有借鉴之处。但是，本文在构建综合单价调整方法时假定影响综合单价调整的其他因素不变，仅针对工程量减少的单因素对综合单价的影响进行了分析。因此，对于多因素影响综合单价调整的情况有待更多的研究者进行探讨。

［1］董红利，姜玉林，白洁. FIDIC 合同条件下工程量变更引起的合同价款调整方法研究［J］ . 工程经济，2015 (3):18-23.

［2］吴书安. 工程变更的分类控制［J］. 建筑经济，2007 (7):81-84.

［3］潘晖. 工程量变化较大引起的价格调整［J］. 基建管理优化，2006，18 (1):13-16.

［4］陈静. 基于状态补偿的工程量偏差对合同价款的影响及调整研究［D］. 天津:天津理工大学，2014.

［5］严玲，赵超超. 基于工程量变化的措施项目费调整研究［J］. 建筑经济，2013 (9):46-50.

［6］杜浩. 综合单价与合同价款探析［J］. 山西建筑，2010，36 (27):242-243.

［7］孙玉红. 工程量清单计价模式下的工程量变更风险分［J］.建筑经济，2006 (7):219-221.

［8］余群舟. 基于工程量变化单价调整理论及方法分析［J］.建设监理，2006 (1):50-51.

［9］程建华，王辉. 新清单中工程变更综合单价的确定［J］.工程管理学报，2013，27 (5):83-87. PMT