模糊Petri网在液压提升机液压系统诊断中的应用

方　 　彪，朱　小　明，2，杨　丽　红（．上海理工大学　机械工程学院，上海200093；2．上海豪高机电科技有限公司，上海2002）

模糊Petri网在液压提升机液压系统诊断中的应用

方 彪1，朱小明1，2，杨丽红1
（1．上海理工大学机械工程学院，上海200093；2．上海豪高机电科技有限公司，上海201102）①

为了提高液压提升机的可靠性，基于液压系统故障的模糊性特点，提出了模糊Petri网（FP N）与矩阵结合的建模及推理方法，将Petri网的理论与模糊推理规则有机结合在一起，采用矩阵解决复杂的推理过程，具有高效准确地并行推理能力。通过历史统计的故障案例，建立基于FP N的液压系统的故障诊断模型，利用此方法可以快速、准确地计算出各个库所的可信度，并可以对初始库所重要度进行分析，大幅减少诊断时间。以液压提升机的提升故障为例，验证了该算法的正确性和高效性。

模糊Petri网；模糊产生规则；故障诊断；液压提升机

随着液压技术的发展，其在工程机械、工业设备、石油勘探、石油钻采、军工等行业得到了广泛的应用。一旦其系统出现故障，会危及到整个设备的安全，甚至是操作人员的人身安全。因此人们对液压系统的稳定性、可靠性的要求越来越高。然而液压系统中液压油在部件和管路中的流动状况，外界是看不到的，并且故障发生有异步并发的特点，这就给分析与诊断带来了较大的困难，要求使用者具备较强的判断和分析故障的能力，从而能在机械、电气、液压复杂的关系中找出故障部位和原因，快速、准确地排除故障。故障诊断专家们对此经过大量的研究，希望能够在元件动作信息和管路液流不可见的状况下，进行较为精确的故障诊断。

液压提升机［1］，又称为液压绞车，是一个典型的集机、电、液、传感器一体化的产品，广泛应用于矿山开采、石油开发、工程建筑与运输等行业。随着石油工业的蓬勃发展，为其提供了广阔的应用平台，液压提升机已成为钻机钻台、储罐倒装、海洋石油平台升降用的主要载物提升设备［2 3］。为提高其液压系统的可靠性和稳定性，以适应复杂的石油勘探、石油钻采的应用环境，需要对其系统进行故障检测和诊断。当前运用人工专家系统、模糊理论和神经网络并行的综合分析诊断已经得到深入的研究。但是这些技术还存在局限性，在诊断能力、适用性、周期性、实时性与经验知识获取等方面还不尽如人意。

FP N［4］是一种能够解释系统的动态行为和结构信息，并能图形化地表达系统信息的网络模型，基于FP N的模型可以描述许多并行和并发行为的故障，它能够将知识表示和诊断推理融为一体，完成从知识描述到过程的诊断推理，利用矩阵计算即可快速获得诊断结果。特别适合于在线事件动态系统的建模和推理［5 7］，并且已经被证明在电力系统故障检测以及计算机集成制造中取得了很好的效果［8 10］。本文针对液压提升机存在的一些问题，在FP N现有的理论方法和研究成果上，对其建模和应用，并进行探讨。在此基础上，引入库所，托肯值和变迁规则的概念，并据此建立故障模型［11］。其后在正向推理故障传播中，对故障的状态进行快速而准确的评断。在逆向推理中，利用了逆向推理策略，实现了验证其有效性的要求。

1 模糊Petri网应用的理论基础

1．1 FP N表达规则

FP N是由库所P和一个变迁T所产生，为了更明确的体现其库所的动态性，使用一个9元组来表达其模型［12］，因此将它定义为：

FP N＝｛P，T，I，O，K，L，μ，α，λ｝

其中：P＝｛P1，P2，…，Pn｝为库所的故障集合；T＝｛T1，T2，…，Tn｝为变迁动作的有限集合；I（O）：T→P∞，是输入（输出）函数，反映变库所输入（输出）映射关系；K＝｛K1，K2，…，Kn｝表示托肯的有限集合。有k→t；μ＝（μ1，μ2，…，μn）T为库所事件pi模糊故障概率集合；α＝（α1，α2，…，αn）T，α为故障事件pi的置信度向量；λ＝（λ1，λ2，…，λn）T为变迁规则的阈值集合。其中λj表示变迁tj点火的阈值，λj∈（0，1），j＝1，2，3，…，m，是由专家经验结合历史数据给出；L＝diag（l1，l2，…，lm）为变迁规则的可信度矩阵，其中lj表示变量的可信度。lj∈（0，1），j＝1，2，3，…，m。

1．2 FP N表达形式

对于任意变迁t来说，其所有输入库所的标记值与相应的输出弧上的权值乘积之和要≥变迁的阈值。因此在模糊产生系统中，用一棵与或树来概括这种前提到结论的形式。在每个产生系统中都包括大量的与或树［13］。模糊产生式规则的图形表示形式如图1所示：

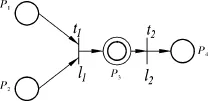
图1 模糊规则的表示

1．3 FP N的建模方法

FP N模型采用置信度规则［14］即用模糊命题合取式的真值来取各子式真值的最小值，用模糊命题的析取式来获取各子式真值的最大值。并分为以下2种。

1．3．1 多因多果模式：

IFPI1andPI2and…andPInT H E NPOk。变迁前真值不变，则变迁后命题Pok的置信度为：αOk＝minαI1，αI2，…，αIn。如图2a所示。

1．3．2 竞争模式

IFPI1orPI2or… orPInT H E NPOk（C F＝l1，l2，…，ln）变迁前提部分规则保持不变，变迁后命题pok的置信度如图2b所示：αk＝max｛α1·l1，α2·l2，…，αn·ln｝。

图2 FP N与模糊产生式规则的相互对应关系

2 FP N在应用中的推理算法

在FP N诊断系统中常用正向推理，反向推理和正反向混合推理3种推理策略。本文采用了正向矩阵推理和反向推理的策略。

2．1 正向推理运算算子定义

在FP N模型的推理中，为了清晰、准确、简洁表示矩阵推理运算，定义了两个特殊算子［14］。定义A，B和C都为m×n维矩阵。

1）：C＝A B，A，B和C均为m×n的矩阵，则cij＝max（aij，bij），i＝1，2，…，m，j＝1，2，…，n。

2）：C＝A B，A，B和C分别为m×p，p× n，m×n的矩阵，则cij＝max｛aik·bkj｝，i＝1，2，…，m，j＝1，2，…，n。

由于计算机咨询专家系统有良好的推理能力，在此理论基础上结合上述的定义算子可得置信度公式［4］：

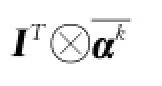
2．2 基于FP N的反向推理的原理

基于FP N的反向推理集合的定义是：可达库所集合（R S）：库所Pi经过激活规则所能到达的所有库所的集合；立即可达库所集合（IR S）：库所Pi经过一次变迁就能到达的库所Pj则称Pj是Pi的立即可达集合，Pi是Pj的反向立即可达集合反向。非立即可达库所集合（RIR S）定义跟立即可达集合类似但是需要不止一次变迁；相邻库所集合（A P）：库所Pi经历同一变迁的所有库所的集合。

反向推理是先由目标故障状态到找出目标证据的推理，其主要思想是假设故障目标存在，然后在库所中查找支持假设故障的结论规则，再验证该规则的假设条件是否成立，若前提能与己知的故障信息匹配并得到满足，则假设成立，否则，把规则的前提作为子目标重复上述过程，直到所有的子目标得到证明为止。反向推理利用积累的维修经验值与正向变迁点火值进行推理。其优点是简单，并有较高的准确率。但是其主要缺点是选择初始目标的盲目性［15］。其步骤如下：

①建立库所的可达库所集合（R S）Pi；再设置标志数组flagPi，并将其初始化为0，其中i是变迁和库所的个数。当诊断系统路的变迁阈值λ（t）＜变迁触发阈值0．5时，则把对应的flagPi置位为0。不再遍寻此路径。并从第i＋1开始继续比较；并把能触发的底时间放入立即可达库所集合（IR S）中。

②根据所要诊断的故障，当筛选出所有能触发的事件后，比较所有底事件的路径把置信度大小，从置信度最大的开始寻找优先诊断顺序；并把变迁超过一次的放入非立即可达库所集合（RIR S），把变迁路径目标库所相同的放入相邻库所集合（A P）。

③在立即可达库所上分析直至下溯到最小割集的底事件，并检验其是否为故障源；当回答为是，即表明故障找出，推理结束。否则继续。

④当③的路径被排除后则置位为0，返回步骤选择非立即可达路径，直至找到故障源。

3 在液压提升机中的实例分析

3．1 FP N模型的建立

运用模糊产生式规则［14］并基于历年售后故障记录以及配合专家经验知识，就能建立模糊产生式规则的诊断知识库。其液压系统原理图如图3所示。把这些故障症状与原因汇总起来做成如表1所示的事件库所。本文中分析的故障症状发生参数主要来源是上海某机电有限公司参与设计的液压提升载物机在售后维修的原始累积数据。从中按照时间顺序得出总故障次数及各个故障与伴生故障出现次数，其数据片段如表2所示。图4为对应的FP N模型。

图3 液压提升机液压系统原理

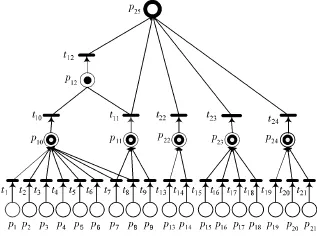
图4 液压提升系统的FP N模型

表1 液压提升系统的FP N模型对应事件

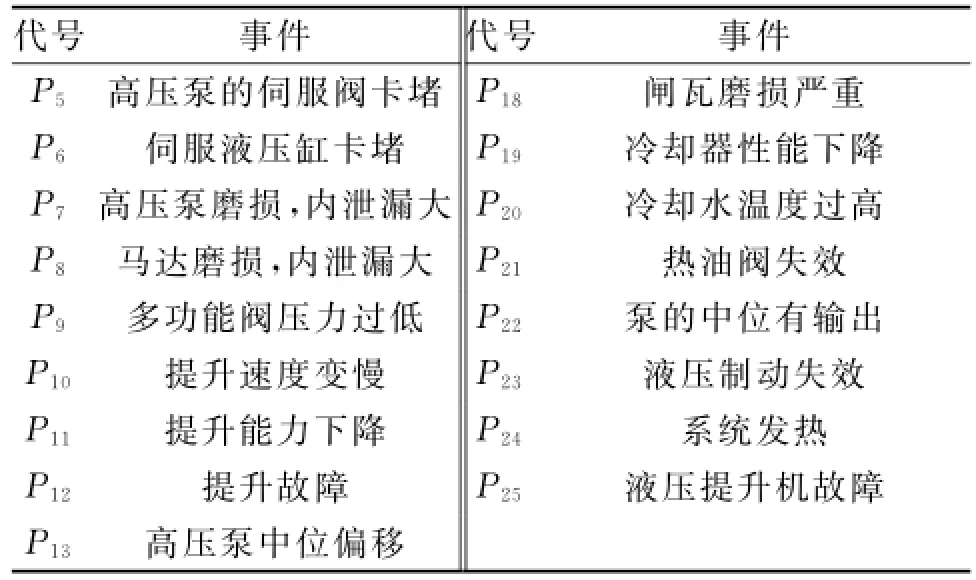
表1（续）

所占比例代号　　历史故障统计次数P1　70　0．37　P13　83　0．46 P2　66　0．34　P14　71　0．37 P3　84　0．46　P15　82　0．43 P4　72　0．38　P16　102　0．53所占比例　　代号　　历史故障统计次数

表2（续）

3．2 正向推理

当没有确切的故障现象发生，而监测系统或操作人员感觉到提升机工作提升不稳定而又不能确认时，则选择路径进行正向推理，得到可能发生的故障及故障严重程度等故障信息。经过比较表2对应的确定事件所可能引发的故障的严重程度以及故障引发次数，并依此可得到所有故障事件对应重要度等级如表3所示。

表3 初始库所重要度分析

根据实际情况与经验总结，可以确定故障等级重要度如表4所示。

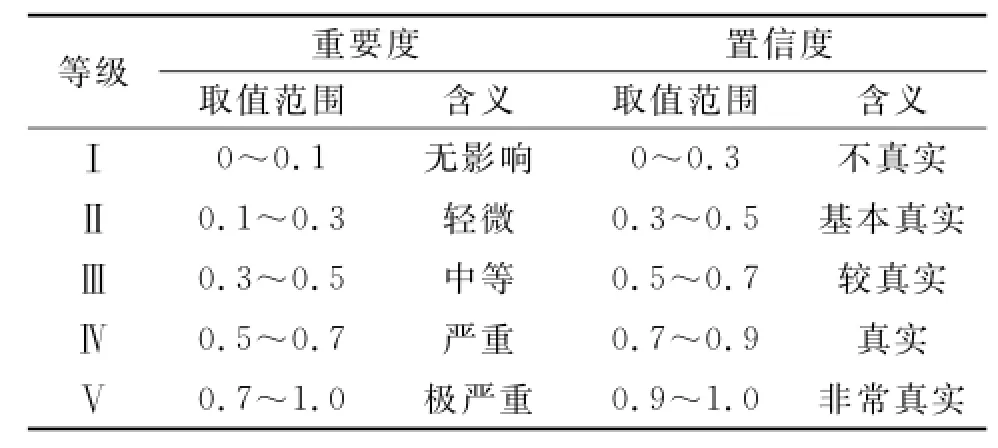
表4 故障事件重要度列表

利用表4中各个事件对应的重要度数据，再根据模糊规则、专家知识及历史数据等，就能设定初始置信度α、可信度L、及阈值λj。

L＝diag（0．82，0．80，0．88，0．90，0．950．90，0．92，0．94，0．96，0．92，0．90，0．92）

α0＝（0．65，0．60，0．70，0．60，0．80，0．85，0．80，0．80，0．65，0，0，0）T

λ＝（0．3，0．4，0．5，0．5，0．5，0．5，0．5，0．5，0．6，0．5，0．5，0．5）

输入与输出矩阵为：

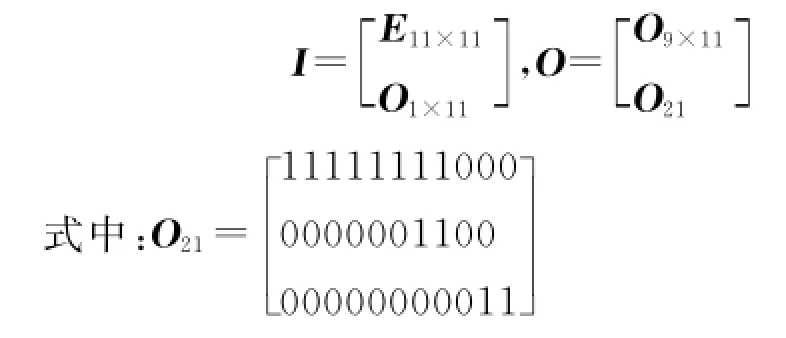
将相关数据代入式（1）并用图5的C＋＋程序计算得：

α1＝0．65，0．60，0．70，0．60，0．80，0．85，0．80，0．80，0．65，0．765，0．752，0）

α2＝（0．65，0．60，0．70，0．60，0．80，0．85，0．80，0．80，0．65，0．765，0．752，0．703）

α3＝（0．65，0．60，0．70，0．60，0．80，0．85，0．80，0．80，0．65，0．765，0．752，0．703）

α3＝α2正向推理结束，获得各事件的可信度，即概率重要度。由计算结果可知：P10提升速度变慢的置信度为0．765，P11提升能力下降的置信度为0．752，P12提升故障的置信度为0．703。由此可见提升速度变慢是导致发生故障预警的首要原因。在此基础上再做进一步分析去检修以预防故障的发生。

图5 液压提升系统的FP N模型计算程序

由液压提升系统的FP N模型，正向推理故障状态得出表5所示信息。相关人员就能根据故障状态有效地预防故障发生，从而提高提升系统的安全有效性。

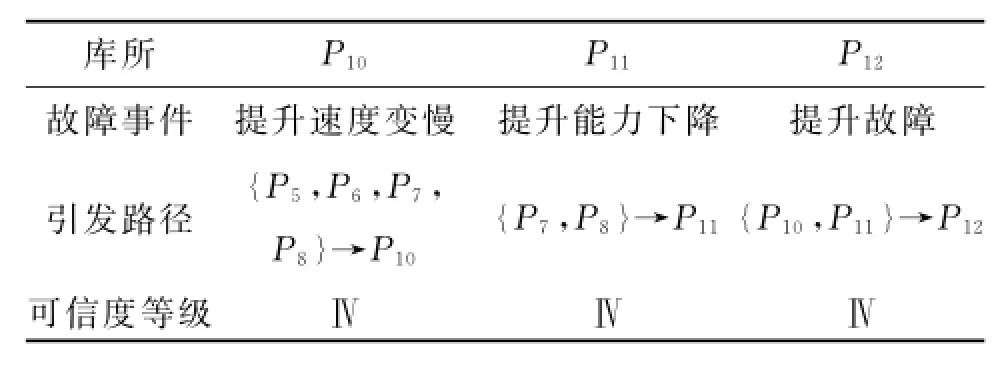
表5 正向推理故障传播状态结果信息

由上表可知在可信度等级相同的情况下，通过比较初始库所重要度可以得出工作人员检修的优先顺序是从P6开始。

3．3 反向推理

当确定有故障现象发生时，例如出现液压制动失效的故障时。引发库所P25为最终目标库所，它的路径为非立即可达库所（RIR S）的P23液压制动失效，即P25→P23。由于对应的变迁t23没有对应的托肯值因此继续向最小割集寻找。能触发P23的路径有立即可达库所（IR S）的P15，P16，P17，P18。即泵控回路压力打不开制动阀P23→P15、制动液压缸卡堵P23→P16、制动电磁阀卡堵P23→P17、闸瓦磨损严重P23→P18。对应的变迁置信度为：

α（P15）＝0．70，α（P16）＝0．75，α（P17）＝0．80，α（P18）＝0．75

触发的阈值分别为：

λ（P15）＝0．6，λ（P16）＝0．4，λ（P17）＝0．5，λ（P18）＝0．5

则λ（P16）不被触发，置位为0并归集到flagPi中。其他3条路径对应的可信度分别为：

l15＝0．92，l17＝0．96，l18＝0．90

分别计算P23的模糊托肯值为：

α23（P15）＝α（P15）×l16＝0．70×0．92＝0．64

α23（P17）＝α（P17）×l17＝0．80×0．96＝0．77

α23（P18）＝α（P18）×l18＝0．75×0．90＝0．675

通过比较得出α23（P17）为最优路径，即优先寻找制动电磁阀是否发生故障，如果技术人员按照此路径检修并判断正是故障发生则推理结束。否则依次选择其他立即可达路径，或者从新选择非立即可达库所直到找出故障为止。

4 结论

通过故障诊断的需求并结合FP N的特点，利用图形方法与矩阵计算相结合的正反向推理策略进行在线诊断，故障判断可以准确到液压系统的元部件。并通过某公司的售后故障处理记录从中选择的故障实例来进行验证，证明了该方法是一种比较有效的并能够帮助操作人员在液压系统应用过程中进行故障检测的行之有效的方法。在推理过程中运用的程序语言算法，让系统能根据故障发生的历史统计数据来自动分析各库所变迁的概率，使得诊断系统更加智能。此外，基于FP N的液压系统诊断技术应用研究相对较少，本文将对其他的液压系统故障检测与诊断的建模过程有一定的借鉴意义。

［1］ 朱小明，孙骞，杨丽红．液压提升机的工作原理及其维修［J］．流体传动与控制，2012，53（4）：42 44．

［2］ 富利波．M Y Q2500型2500t门式液压提升系统在超大型设备吊装中的应用［J］．石油化工建设，2013（1）：33 39．

［3］ 杨世平，敖沛，胡朝刚．液压起升钻机同步系统的设计［J］．石油矿场机械，2008，37（5）：43 47．

［4］ 袁崇义．Petri网的原理与应用［M］．北京：电子工业出版社，2005．

［5］ 黄敏，林啸，侯志文．模糊故障Petri网建模方法及其应用［J］．中南大学学报，2013，44（1）：208 215．

［6］ M U R A T A T．Petri nets：Properties，analysis and ap plications［J］．Proceed of the IE E E，1989，77（4）：541 580．

［7］ G U Jun．A nalysis on A uto mobile engine failure diagno sis based on genetic algorith m［J］．A dvancedM ateri alsResearch，2012（10）：490 495．

［8］ 汪志斌．Petri网及其在制造系统建模与控制中的应用［M］．北京：机械工业出版社，2004．

［9］ LI Xiaoou，LARA ROSANOF．Dynamic Knowledge Inference andLearningunderA daptiveFuzzyNet Framework［J］．IE E E Trans on System，Man，and Cy bernetrics：Part C A pplications and Reviews，2008，30 （4）：442 450．

［10］ LUOX，KEZUNOVICM．Im plementing Fuzzy Rea soning Petrinets For Fault Section Estimation［J］．IE E ETransonPowerDelivery，2008，23（2）：676 685．

［11］ 汪惠芬，梁光夏．基于改进模糊故障Petri网的复杂系统故障诊断与状态评价［J］．计算机集成制造系统，2013，19（12）：3049 3061．

［12］ 吴双，何正友，钱澄浩，等．模糊Petri网在高速铁路牵引供电系统故障诊断中的应用［J］．电网技术，2011，35（9）：79 85．

［13］ 杨健维，何正友．基于时序模糊Petri网的电力系统故障诊断［J］．电力系统自动化，2011，35（15）：46 51．

［14］ 李厦，乌建中．模糊Petri网在液压同步提升系统故障诊断中的应用［J］．中国工程机械学报，2006，4（1）：68 71．

［15］ 方桂花，赵永，李旭省．模糊Petri网在液压泵故障诊断中的应用研究［J］．机床与液压，2011，39（19）：155 158．

Appiication of Fuzzy Petri Nets in Hydrauiic Hoists System Fauit Diagnosis

FANG Biao1，ZHU Xiao ming1，2，YANG Lihong1
（1．College of Mechanical Engineering，Shanghai Universitu for Science and Technologu，Shanghai200093，China；2．Haogao Mechanical Technologu（Shanghai）Co．，Ltd．，Shanghai201102，China ）

To im prove the reliability of hydraulic hoists，and then，the modeling and reasoning methods of co m bining fuzzy Petri nets with matrix operation was proposed based on the fuzzy fea ture of hydraulic system fro m hydraulic hoists．It co m bines the theory of Petri nets and the rules of fuzzy reasoning and solves the com plex reasoning，which could do parallel inference efficiently and exactly．The fuzzy Petri netin hydraulic system fault diagnosis modeling was based on histori cal statistics failure case．It dem onstrates that this theory could acco m plished calculate the credi bility of initial database quickly and accurately，besides the method also reduced the diagnosis time after analyzing the initial database．Finally，a hydraulic hoists system was taken as the exa m ple to validate the correctness and efficiency of proposed approach．

fuzzy Petri nets；fuzzy production rules；fault diagnosis；hydraulic hoists

T E951

B

10．3969／j．issn．1001 3842．2015．06．016

1001 3482（2015）06 0068 06

①2015 01 10

上海市自然科学基金资助项目（12Z R1420600）

方 彪（1989 ），男，江苏宿迁人，硕士研究生，主要从事工程机械液压系统与设备的研究工作，Email：15751871750＠163．com。