车轮传感器电磁分布研究
卢迪++周三强
摘要:针对车轮传感器是保证铁路运输安全、提高运输效率及管理系统自动化所必需的一种核心设备问题,通过分析了车轮传感器的工作原理,利用Ansoft Maxwell 3D有限元仿真软件对传感器电磁系统进行了仿真,在建立合理的车轮传感器电磁仿真模型的基础上,分析了线圈的位置和角度对传感器电磁分布产生的影响,优化了发送和接收线圈的结构,对车轮传感器的设计和研制具有一定的指导意义.
关键词:传感器;电磁场;线圈;Ansoft
DOI:10.15938/j.jhust.2015.02.010
中图分类号:U284.47
文献标志码:A
文章编号:1007-2683(2015)02-0053-04
0 引 言
随着经济的高速发展,我国在铁路建设方面的投入大幅增加,对于铁路设备和铁路安全运行的要求也愈来愈高.车轮传感器是保证铁路运输安全、提高运输效率及管理系统自动化所必需的一种核心设备.同前,国内外流行的车轮传感器主要有无源和有源两种形式.而无源传感器由于自身的不足,只能在列车运行速度高于5km/h的时候才可以使用,所以现在大多数都采用有源车轮传感器
电磁感应车轮传感器是有源车轮传感器的一种,种类繁多,应用最为广泛.然而其详尽的磁场分布规律和定量分析的文献围内外公开的甚少,准确分析和计算车轮传感器中电磁系统的磁场分布是传感器优化设计和研制的关键问题,
1 车轮传感器的工作原理
电磁感应车轮传感器主要是利用线圈互感原理研制的.当列车车轮通过计测点时,车轮传感器接收端的磁通量会发生变化,从而得到轮轴信息.发送端和接收端一般由铜质线圈和磁性材料构成,但由于磁性材料的温度稳定性差,我们采用了空心线圈,车轮传感器的电磁系统包括发送线圈和接收线圈,发送线圈安装在钢轨外侧,接收线圈安装在钢轨内侧,车轮传感器的装置图如图1所示:
2 车轮传感器有限元建模
目前,工程技术领域内常用的数值模拟方法有:有限单元法、边界元法、离散单元法和有限差分法,就适用性与应用的广泛性而言,主要是有限单元法.Ansoft Maxwell作为世界著名的商用低频电磁场有限元软件,在实际中有着广泛的应用.此软件把复杂的数学计算放到后台进行处理,使用者可以直接面向需要解决的问题,建立模型,设置材料属性,参数及其他相关的求解设置,然后进入后处理步骤,得到相关电磁场和参数的详细信息.
2.1 求解器设定和几何建模
车轮传感器的电磁分布属于不对称的非线性开域时变磁场,无法建立二维磁场模型,所以只能利用Ansoft Maxwell 3D进行有限元建模,车轮传感器周围电磁场属于非线性似稳磁场,对于似稳磁场通常采用Ansoft中的涡流场求解器进行仿真分析,
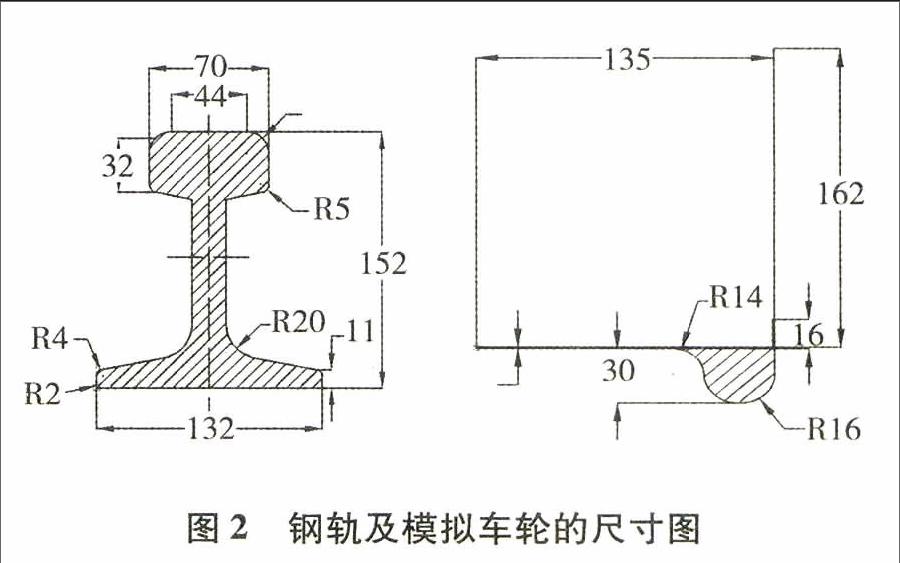
几何建模中主要有发射和接收线圈、车轮和铁轨等几何体.根据铁路用热轧钢轨的标准CB2585-2007中的分类,仿真计算中所用到的钢轨采用50kg/m的钢轨,车轮采用铁道行业标准TB/T10IO-2005中所规定的RD33型轮对,然而在实际的仿真中,由于车轮和铁轨的尺寸过大,剖分的网格数过多,对计算资源要求很高,所以我们对其进行了简化处理,钢轨和模拟车轮的具体尺寸如图2所示,钢轨的长度设定为200mm.
2.2指定材料属性
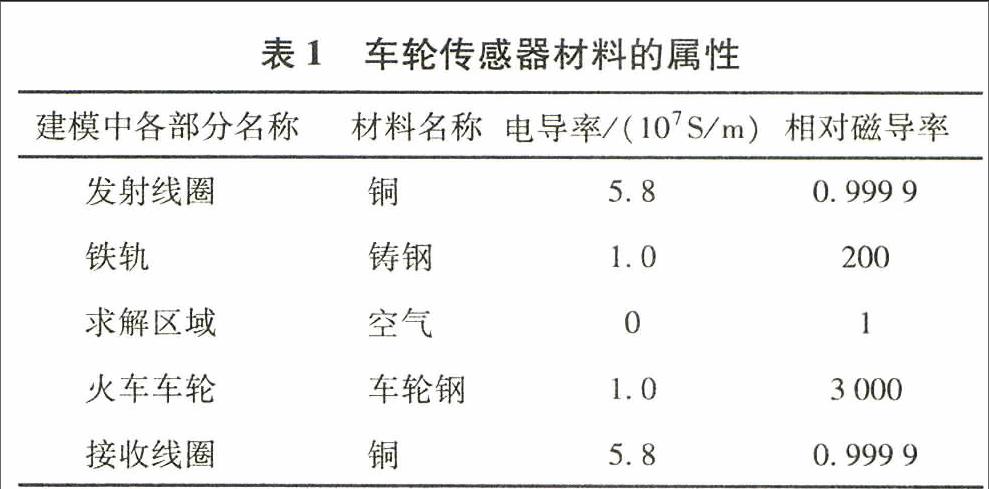
车轮传感器的材料属性如下表所示.
2.3激励源和边界条件设定
由于车轮传感器主要是利用发送线圈和接收线圈的互感原理设计的,发送线圈需要通过一定的电流,接收线圈中才会感应出信号.仿真时在发送线圈添加240mA的正弦电流信号,接收线圈添加为被动激励信号,在涡流场求解器中可以利用软件自动计算得出接收线圈中感应出的信号值.为了提高仿真速度,计算过程中设定几何边界为阻抗边界.引入阻抗边界条件后,可以对透入深度进行忽略,减小了器件表层划分过于细致带来的庞大计算量.
3 仿真结果分析
车轮传感器是利用线圈的互感设计的,发送线圈和接收线圈的位置和角度对车轮传感器的灵敏度有着至关重要的影响,要设计出最优的传感器结构,必须先确定出其适合的角度和位置.本模型是以Maxwell中的3D涡流场进行模拟仿真的,可以利用接收线圈中的感应磁通量来衡量其最优结构.模型的YOZ平面投影图和网络剖分图如图3所示.
数据由于接收线圈位置受车轮轮缘导致的空间限制,只能试着改变发射线圈的位置和角度来达到优化传感器结构的目标,本文以发射线圈的几何相对位置Y=82mm,Z=72mm,α=65°作为基准位置,分别改变发射线圈的横向距离y、纵向距离Z和角度α,通过对接收线圈中磁通量的变化进行分析,利用Maxwell软件中的计算器Fields Calculator对磁通量进行计算,得到的接收线圈内部截面磁通量值如表2,3,4所示.
由于钢轨周围的空间限制,实际的发射线圈调整角度也受到限制,我们只对40°至85°进行了仿真.从表2我们可以看出随着发射线圈角度的增加,接收线圈中的磁通量有一定的波动,考虑到本文是利用无车轮和有车论时磁通量的差值来进行车轮轮轴的测量,我们选择磁通量值较大且有、无车轮时差值较大的作为线圈的最佳安放位置.当α=65°有时接收线圈的磁通量值比较大,并且与无车轮时接收线圈的磁通量差值最大,因此选α=65°作为接收线圈最佳安放角度.
同样由于钢轨周围的空间限制,实际的发射线圈水平位置和垂直位置也受到限制,线圈不可能无限的接近铁轨,根据铁路部门的相关规定以及在实际安装中装置的安装空间限制,我们只对水平位置Y=74mm至y=108mm和垂直位置Z=60㎜至Z=78mm之间的位置进行仿真,从表3和表4我们可以看出,水平位置y=82mm时有车轮时接收线圈的磁通量值最大,并且与无车轮时接收线圈的磁通量差值最大;垂直位置Z=72mm时有车轮时接收线圈的磁通量值比较大,并且与无车轮时接收线圈的磁通量差值最大,所以选水平位置y=82mm.垂直位置Z=72mm作为接收线圈最佳安放位置.
通过对以上3个表格进行分析可以确定线圈的最佳安放位置为y=82mm,Z=72mm,α=65°.与传感器处于最佳安放位置时,传感器的磁感应云图,如图4和图5所示,磁感应矢量图,如图6和图7所示.此时接收线圈中感应到的磁通量值最大且与无车轮时磁通量差值最大,如果按这个结构设计传感器的电磁系统,可以提高传感器信号的灵敏度.
5 结 论
车轮传感器是保障铁路安全运营的核心设备,本文利用Ansoft Maxwell 3D有限元仿真软件对传感器电磁系统进行了仿真,通过对仿真结果的数据分析可得,当线圈的水平位置为82mm、垂直位置为72mm、角度为65°时,传感器探头线圈的灵敏度最高.

