矿山台阶爆破震动速度预测方法的研究
李小武,周 铭,胡 韬,代雨昊,何皇兵(昆明有色冶金设计研究院股份公司,云南 昆明 650051)
矿山台阶爆破震动速度预测方法的研究
李小武,周铭,胡韬,代雨昊,何皇兵
(昆明有色冶金设计研究院股份公司,云南昆明650051)
摘要:针对某露天矿山采场附近居民房屋出现裂缝的问题,进行矿山居民房屋现场测震,并现场实验检验了传统萨道夫斯基线性回归方法与BP神经网络预测震动速度的两种方法的可靠性,采用BP神经网络方法进行爆破震动质点速度的预测,再通过调整爆破设计降低爆破震动,保障了房屋的安全。
关键词:矿山爆破;爆破震动;神经网络预测;房屋安全
0 引 言
爆破技术在采矿、铁路及国防建设等方面有着广泛地应用,爆破工作不可避免的会产生一些负面效应,如爆破震动、冲击波、飞石、噪声等,而爆破震动是爆破施工作业中最严重的负面效应。
减小爆破施工负面效应的最重要方法就是预测爆破震动。实测结果表明:爆破震动强度与炸药量、爆心距、岩土性质以及场地条件等因素密切相关。国内外采用预测爆破震动速度的公式不尽相同,见表1[1]。

表1 世界各国对爆破震动质点振速峰值预测公式Tab.1 Worldwide prediction formula of the vibration velocity peak of blasting vibration particles
人工神经网络的出现,国内外许多学者采用神经网络对爆破震动速度进行预测,在众多神经网络的算法中,BP人工神经网络在爆破震动峰值振速预测中应用最多,Mohamed、Amnieh、徐全军、沈蔚等采用BP人工神经网络进行爆破震动峰值预报[3-8]。
1 工程背景
某矿山在开采过程中,与采场周边的村民发生了比较突出的矛盾之一是采场台阶爆破作业对周边的民用建筑房屋的震动损害与破坏,造成企业与村民关系紧张,给矿山的建设与生产带来了一定的影响。
根据采场目前爆破设计的情况,计算得到的爆破震动最大影响距离为113 m,爆破飞石影响为115 m,而爆破确定的安全界线是爆破作业区200 m以外,因此从爆破震动的计算影响范围来讲爆破作业对房屋应该是没有影响的。针对村民多次反映的房屋墙面裂缝等问题,见图1。矿山进行调查后认为主要的原因是:采矿场周围的自建房屋结构简单、房龄偏长和存在隐性的裂缝,抗震等级难以保证;同时,采场爆破加剧了房屋的损坏。为了缓和企业与居民的关系,不至于影响矿山生产,在不考虑对房屋进行搬迁的情况下,寻求降震的方法。

图1 房屋裂缝情况Fig.1 Cracks of house
2 降震技术措施
震动速度的影响因素也就是降震技术中需要处理的因素。根据国内外许多爆破工作者及科研工作者的研究与总结,降震技术措施大致有以下几种方法:
1)爆源控制降震
(1)减小单段最大起爆药量
由萨氏公式分析,可知单段最大起爆药量Q 是3个影响质点速度V的因素中可以进行调控的因素,单段最大起爆药量越大,质点震动速度越大。在矿山实际生产中,可以进行孔内微差起爆的方法,来减小单段最大起爆药量。大量试验研究表明,产生地震效应跟爆破炮孔之间的微差时间有着密切的关系。微差时间的确定有3个原则:①使排间延发时间大于排内延发时间;②选取微差时间应使前后起爆的炸药量产生的地震波互相干扰;③使前后起爆的炸药量产生的地震波主震相不重叠。研究表明,微差时间一般选取30~50 ms为宜。需要根据不同的爆破场地的地质条件和环境,通过试验和长期观察来确定,这种方案爆破技术人员在现场比较容易控制与调整。
[7]列宁:《列宁专题文集·论辩证唯物主义和历史唯物主义》,北京:人民出版社,2009年,第161页。
(2)合理的孔网参数
国内外露天矿山台阶爆破孔网参数多采用“大孔距”爆破参数,大量试验研究表明,在保持每个炮孔负担面积基本不变的情况下,适当地减小排距而加大孔距,不仅可以使爆破效果得到改善,而且能减少爆破地震波效应。工程技术人员长期在现场负责,了解实际地质情况,才能更好地调整好孔网参数。
(3)拥有良好的自由面
爆破试验研究得知,爆破时越靠近自由面的炮孔,产生的爆破震动越小,因此,爆破作业中的每个炮孔必须有自由空间以配合微差技术,从而使后排炮孔爆破产生的压缩波从这些自由面中反射,从而降低爆破震动。随着雷管精度的不断提高,逐孔起爆技术广泛地应用于矿山台阶爆破,为台阶爆破提供了良好的自由面。
(4)选择合适的爆破作用指数
对露天各种大的爆破工程,爆破作用指数的大小很大程度上影响着爆破震动的强度,在一定的范围内成反比关系。因此矿山台阶爆破中应尽可能获得最大松动的爆破条件,以减少爆破震动强度。但该矿山由于生产情况,采用强制的压碴抛掷爆破。
2)截断传播路径进行隔震
采用减震沟减震可以干扰和阻隔爆破地震波的传播,减震沟对爆破地震波起到反射和绕射,降低了爆破地震波的强度,从而加快了爆破地震波的衰减,达到了控制爆破震动的作用。但该方法操作起来复杂,矿山技术上的力量也不足,因此不予采纳。
3 质点震动速度预测
对爆破震动进行预测是采取有效爆破方案的前提。单段最大起爆药量是控制爆破震动影响的关键。在几所居民民房里安装测震仪进行测震,包括爆心距、单段最大起爆药量、台阶爆破处与测震点高程、爆心距方向线与自由面的夹角和测点处质点震动速度,见图2,共收集了16组数据,见表2。根据建筑物安全允许的震动速度,见表3,民房建筑物的允许震动速度为2.0 cm/s,可知其震动并未超过安全允许值,但由于房屋老化,参照相关经验适当地降低其安全允许值为1.5 cm/s,再设计爆破方案,以达到降低爆破震动的原因。采用传统的萨氏公式进行线性回归与智能BP神经网络进行爆破震动的预测。

图 2 爆心距与自由面的夹角Fig.2 Angle between blasting center distance and free surface
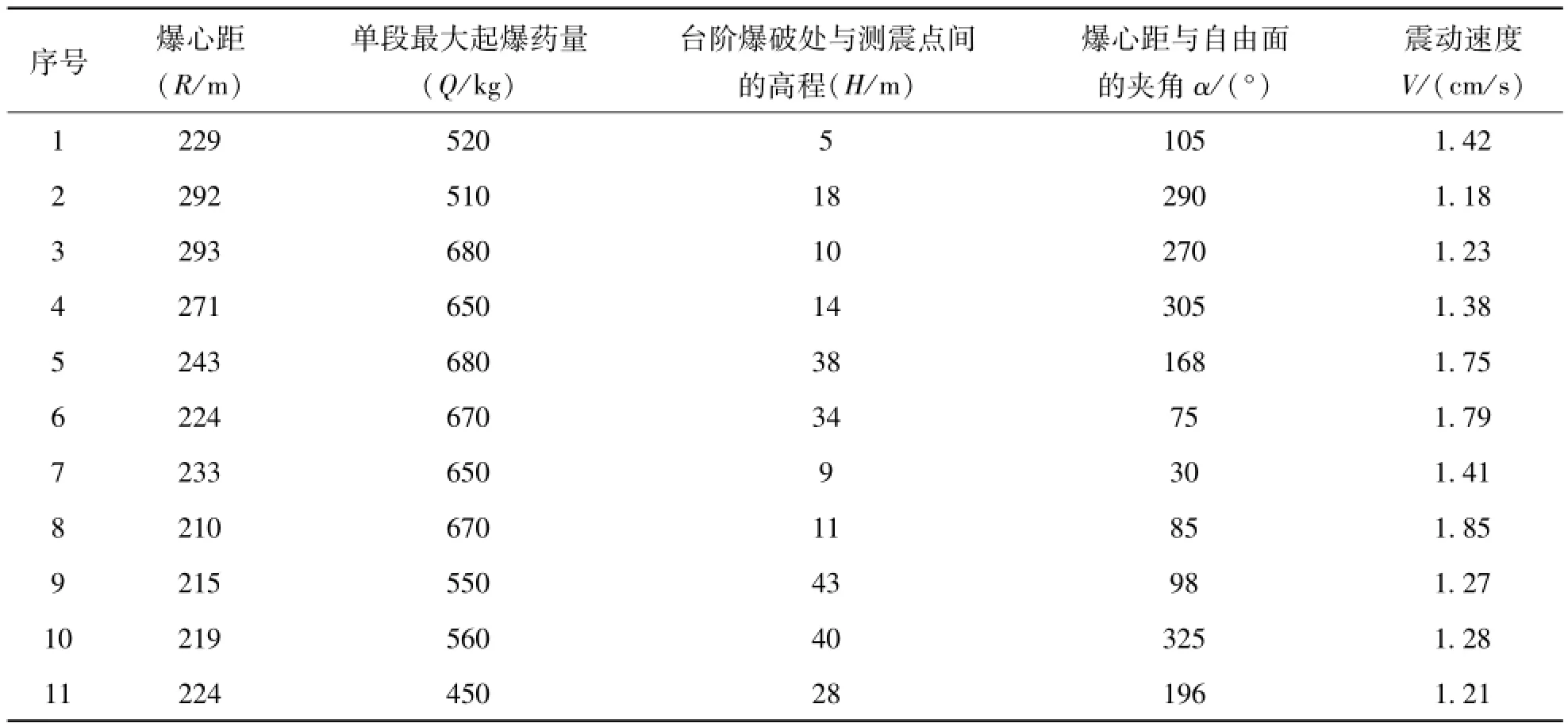
表2 爆破试验震动速度Tab.2 Blasting vibration velocity

序号 爆心距(R/m)单段最大起爆药量(Q/kg)台阶爆破处与测震点间的高程(H/m)爆心距与自由面的夹角 α/(°)震动速度V/(cm/s)12 286 580 16 335 1.11 13 295 600 14 231 1.09 14 278 500 7 256 1.05 15 204 680 24 67 1.95 16 289 640 25 117 1.31
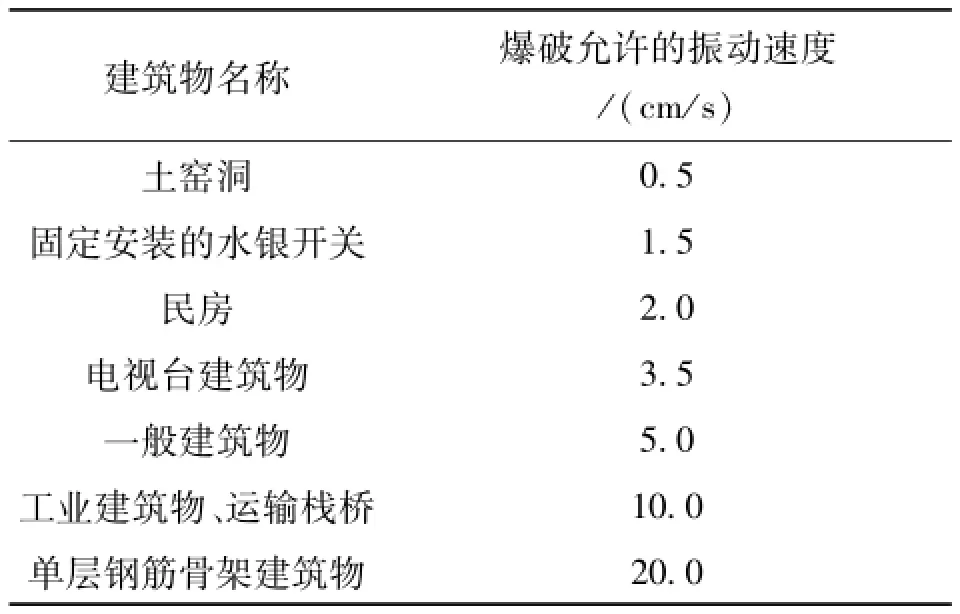
表3 国内建筑物允许震动速度Tab.3 Domestically permitted building vibration velocity
3.1线性回归预测分析
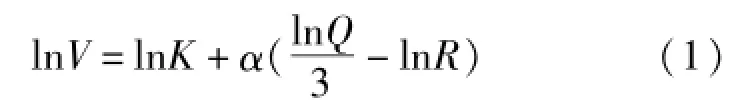
已编入《爆破安全规程》的萨道夫斯基公式是国内计算爆破震动的依据,对萨氏公式等号两端取对数,得到:由于在同一地区,K与α都是常数可知,令y= lnV,x=lnQ-lnR,b=lnK,(1)式简化为y=b+ ax,即lnV与-lnR具有线性关系。由线性回归计算得到K=57.2797,α=1.1037。代入萨氏公式得到:
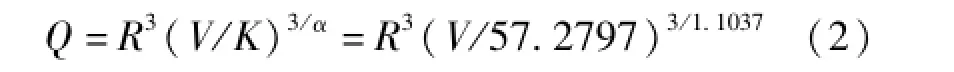
由表3的允许安全震动速度V=1.5 cm/s和房屋离最近的爆破点的距离为204 m,代入公式(2)中得到单段最大起爆药量为425.65 kg。
将K与α的值代入萨氏公式中得到预测爆破震动公式:

将公式(3)计算得到的线性回归震速值与实际测量值进行误差分析,以检验公式的准确性,如表4所示。误差大多数均在10%以内,只有第5、6、9、10及11次超过10%。近年来不少学者对误差大的原因进行研究表明:这是由于测震点与爆破处的高程所引起的[9]。

表4 线性回归震速计算值与实际测量值误差分析Tab.4 Error analysis on the calculated vibration velocity by linear regression and the actual measured value
3.2神经网络预测分析
BP人工神经网络是采用反向传播算法的一种神经网络,它是一种监督训练多层网络的算法,主要原理是通过学习,使网络的输出层的误差平方和达到最小。以爆破震动主要影响的4个因素:单段最大起爆药量Q、爆心距R、测震点与台阶爆破处的高程H以及爆心距与自由面的夹角α为作为神经网络输入;采用3层BP神经网络,以爆破震动速度V作为神经网络的输出。构成1个多个输入单个输出的神经网络,隐含层神经元个数采用6个,其拓扑结构见图3(图中左侧为输入元素,右侧为输出元素)。网络训练数据采用表2中的16组数据,神经网络训练采用的是trainlm函数,误差传递采用的是tansig函数,误差采用的是mse函数,训练步骤设置为4 000步,迭代训练精度达到0.001。用训练好的网络就可以进行爆破震动速度的预测。

图3 神经网络拓扑结构Fig.3 Topology of neural network
4 现场检验
随机进行了9次爆破测震试验用于检验2种爆破震动预测方案的可靠性,试验数据见表5。表中V测1由公式(4)计算得到,V测2由BP神经网络得到,V实由测震仪实际测量得到。从表5中可以看出线性回归的最大相对误差为20%,不超过10%的次数为6次,而神经网络的最大相对误差为15.38%,不超过10%的次数为7次。神经网络预测值与实测值的对比及绝对误差的对比分别见图4、图5。从图4中可以看出神经网络预测值贴近与实际测量值附近,图5可以神经网络预测值的绝对误差曲线更接近X轴,因此相比较而言,实验说明了神经网络在预测爆破震动强度时更准确一些。

表5 爆破质点震动速度误差对比Tab.5 Error comparison of vibration velocities of blasting particles

图4 预测值与实测值的对比Fig.4 Comparison between predicted and measured values

图5 预测值与实测值绝对误差的对比Fig.5 Absolute error comparison between predicted and measured values
5 结 语
对设计方案进行爆破质点的震动速度的神经网络方法预测后以调整单段最大起爆药量,并采用孔间微差起爆技术,在房屋进行修补之后再未出现裂缝情况。
1)萨氏公式线性回归分析与BP神经网络均可以用于爆破质点速度的预测,但神经网络考虑对爆破震动强度的影响因素比萨氏公式更多,采用BP人工神经网络方法预测的爆破震动峰值振速更接近实测值,表明了BP人工神经网络方法预测爆破震动强度的优越性。
2)采用在设计中提前预测爆破质点的震动速度,再确定最终的爆破设计方案,为居民房屋的安全提供了保障,改善了企业与居民关系,加快了企业建设进程。
参考文献:
[1]申旭鹏.研山铁矿台阶炮孔爆破地表质点振速峰值预测方法研究[D].北京:北京科技大学,2012:2-3.
[2]刘殿中,杨仕春.工程爆破实用手册[M].北京:冶金工业出版社,2004.
[3]沈蔚,徐全军,季茂荣,等.中深孔爆破震动参数的BP神经网络预报[J].爆炸与冲击,2002,22(4):353 -357.
[4]徐全军,张庆明,恽寿榕.爆破地震峰值的神经网络预报模型[J].北京理工大学学报,1998,18(4):472 -475.
[5]Mostafa Tantawy Mohamed.Artificial neural network for predic-tion and control of blasting vibrations in Assiut (Egypt)limestone quarry[J].International Journal of RockMechanics&MiningSciences,2009,46:426 -431.
[6]Manoj Kh,Singh TN.Prediction of blast induced ground vibrations and frequency in opencast mine:a neural network approach[J].Journal of Sound and Vibration,2006 (289):711-725.
[7]杨佑发,崔波.爆破震动速度峰值的预测[J].震动与冲击,2009,28(10):195-198.
[8]陈德志,朱瑞赓.基于BP神经网络的路堑爆破对邻近民房安全预测的研究[J].岩石力学与工程学报,2002(2):51-54.
[9]张天军,马锐,乔宝明,等.爆破震动中萨道夫斯基拓展式的回归分析[J].湖南科技大学学报:自然科学版,2012(3):12-16.
中图分类号:TD76
文献标识码:B
文章编号:1004-2660(2015)01-0001-05
收稿日期:2015-01-20.
作者简介:李小武(1980-),男,湖南人,工程师.主要研究方向:采矿工程.
Study on the Prediction Method of Vibration Velocity in Bench Blasting
LI Xiao-wu,ZHOU Ming,HU Tao,DAI Yu-hao,HE Huang-bing
(Kunming Engineering&Research Institute of Nonferrous Metallurgy Co.Ltd.,Kunming 650051,China)
Abstract:As cracks were observed in the wall of resident houses near the open stope,vibration measurement on site was carried out.The reliability of traditional Sadov’s linear regression and vibration velocity prediction by BP neural network was examined.The blasting vibration particle velocity prediction of by BP neural network was adopted and the blasting vibration was reduced by adjusting the blasting design,thus ensuring the housing security. Key words:mine blasting;blasting vibration;neural network prediction;housing security

