耳蜗神经网络中语音信号传输的刺激条件信息研究

王风娇，任昱昊，赵 进，段法兵

(青岛大学复杂性科学研究所，山东 青岛 266071)

耳蜗神经网络中语音信号传输的刺激条件信息研究

王风娇，任昱昊，赵 进，段法兵

(青岛大学复杂性科学研究所，山东 青岛 266071)

在耳蜗神经网络对语音信号的刺激响应过程中，针对如何区分编码最有效率的语音信号分量问题，提出了刺激条件信息分布计算方法，研究了给定刺激条件下平均不确定性度的减小。实验结果表明：积分发放神经网络膜电位发放的刺激条件信息不仅能够从统计意义上给出平均互信息的大小，而且清晰地表明信号中各分量的编码效率，确定输入信号中对于互信息量起主要作用的事件分量范围以及内部噪声的可利用性，证实噪声强度与最大刺激条件信息量之间的非单调关系，这些研究结果为进一步探索人工耳蜗动作电位发放的解码方案提供了理论依据。

耳蜗神经网络；语音信号；积分发放神经元；刺激条件信息

0 引言

在神经元网络的信息传递过程中，信息理论在比较神经信息的编码方案和感官系统的神经数据分析中得到广泛应用。比如香农平均互信息经常被用来分析神经元响应中包含刺激信号的信息量的多少，从统计平均意义上表示有关刺激信息的不确定度缩减量[1-2]。但是，在信息的传输过程中，平均互信息量不能体现输入信号中最有编码效率的分量，它是神经网络有关刺激信号集合的统计意义上信息传输特征量。因此，DeWeese与Meister[3]提出事件信息来衡量在神经代码中特殊信号所产生的信息量。在整个响应向量空间，对事件信息进行统计平均得到平均互信息，因此事件信息是平均互信息的一种分解形式[3]。进一步地，由于刺激信号和响应的非对称性，Butts[4]提出了刺激条件信息，定义为在给定一个刺激事件条件下，观测数据中不确定性的平均减少量，对于整个刺激信号空间对刺激条件信息进行统计平均同样得到平均互信息。刺激条件信息在视觉模型数据处理[5]和听觉表层神经细胞[6]的研究中得到了广泛关注，依据最大刺激条件信息可以方便地确定刺激信号中最有编码效率的信号分量[4-6]。

上述刺激条件信息的研究[4-6]虽然注重了每个刺激信号分量对于神经元响应的编码效率，但是没有考虑神经元内部大量自发的电位随机发放活动(内部噪声)对于编码效率的影响。大量的研究表明，神经网络的信息传递和动作电位的协同发放都有噪声的参与，而且噪声起到积极的秩序建设作用[7-9]。本文对于耳蜗神经网络中刺激信号分量的编码效率以及信息传递过程中的噪声作用进行了研究，提出了互信息和刺激条件信息的数值计算方法，实验分析了耳蜗神经网络膜电位积分发放神经元模型的响应特性。刺激信号选为一段语音，不同数目并联神经网络响应的平均互信息结果表明，随着内部噪声强度的增加，语音信号的传输存在最优的噪声环境，此即超阈值随机共振现象[8]。而且，在给定噪声强度下，平均互信息表明信息的增益不需要大的神经元群体，有限数目的神经元就可使得信息传输效率提高约10%，当噪声强度进一步增大时，保持信息增益则需要增加神经网络中神经元数目。进一步地，刺激条件信息分布的实验结果清晰地表明了刺激信号中各分量的编码效率，能够确定输入信号中对于互信息量起主要作用的事件分量范围。而且，刺激条件信息的分布也反映了基于超阈值随机共振机制的内部噪声积极作用，证实了噪声强度与最大刺激条件信息量之间的非单调关系。这些研究结果为进一步探索人工耳蜗的膜电位积分放电刺激的解码方案提供了理论依据，在生物神经元刺激信息处理中具有广泛的应用前景。

1 刺激条件信息与神经元模型

1.1 积分发放神经元模型

基于听觉生理刺激产生机制，本文利用积分发放模型对耳蜗接收语音刺激信号的特性进行模拟。漏电积分发放模型[9-10]虽然是对神经模型的工作机制抽象简化后的产物，但是能非常确切地描述神经元动作电位的基本特性，因此在听觉生理模型中得到广泛应用[9-10]。耳蜗神经元在一个频带处理区域内，具有同样生理性质的神经元呈并联阵列排列[9-10]，设每个积分发放模型描述的神经元膜电位Vi(t)满足

(1)

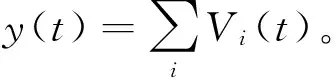
1.2 刺激条件信息计算方法

设神经元输入刺激信号为x(t)，神经元响应为y(t)，那么刺激信号和响应之间的互信息[11]为

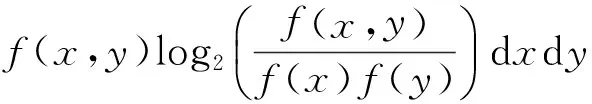
(2)

这里f(x)和f(y)分别为x(t)与y(t)的概率密度，二者的联合概率密度为f(x,y)。平均互信息是对于刺激信号总体的概率进行加权平均，反映了两个随机变量集合之间的信息传递，但是不能反映刺激信号集合内个体对于信息传递的贡献。因此，Butts[4]提出了刺激条件信息

(3)

表示了在给定刺激信号下，观测数据中不确定性的平均减少量。这里，f(x|y)和f(y|x)为条件概率密度。在刺激信号向量空间内，对于刺激信号集合进行概率平均得到平均互信息

(4)

因此，刺激条件信息可以看成平均互信息在刺激信号空间中进行投影的分量。

f(xi,yj)≈kij/(KΔxΔy)

(5)

X与Y的概率密度分别为

(6)

条件概率密度分别计算为

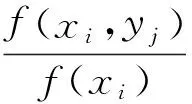
(7)

于是得出刺激条件信息数值计算公式

(8)

2 结果

积分发放神经元外部刺激语音信号如图1所示，表示一段语音信号“The girl lost in the forest”，持续时间2.5 ms，纵坐标代表了幅值的大小。图2给出了当门限值Vth=0.95 V时，平均互信息I(x,y)随着神经元数目N以及所加噪声强度σ的变化。由图2可以看出，随着内部噪声强度的增加，语音信号的传输存在随机共振现象，对于相同数目的神经元网络来讲，平均互信息随着噪声强度的增加存在一个最优值。在图2中当噪声强度σ=0.15W/Hz时，神经元个数N=10所对应的平均互信息量I=1.414 bits最大，而N=100时所对应的平均互信息量I=1.392 bits。这一实验结果和经典的超阈值随机共振[8]现象不同，经典的超阈值随机共振[8]现象是指随着内部噪声强度的增加，语音信号的传输存在最优的噪声环境，相同噪声强度下，神经元数目与互信息成正比例增加，而本文实验结果表明在给定噪声强度下(不再强调最优噪声环境)，有时平均互信息表明信息的增益不需要很多的神经元群体[14]，仅仅需要有限数目的神经元就可提高信息传输效率，比如噪声强度σ=0.15W/Hz，10个神经元所得到互信息比100个神经元所获得互信息要大，最大互信息与无内部噪声相比大约提高10%。图2还可以看出，当噪声强度进一步增大时(如σ=0.4W/Hz)，获得相同的信息增益则需要增加神经网络中神经元数目。

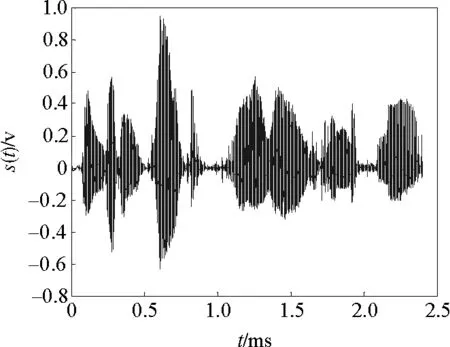
图1 语音信号“The girl lost in the forest”的波形Fig.1 Speech waveform of “The girl lost in the forest”

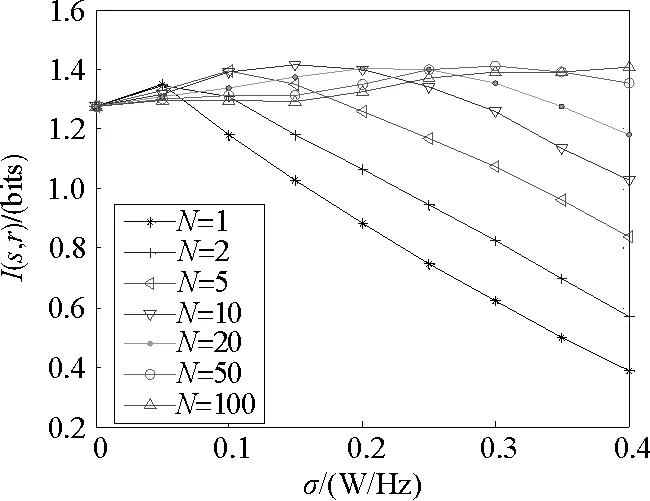
图2 不同并联神经元数和随噪声强度下的平均互信息量

图3 N=10时的刺激条件信息量

图3a为σ=0.15W/Hz，N=10时，神经元网络对含噪语音信号响应的刺激条件信息分布，横坐标代表响应所对应的刺激条件信息量大小，纵坐标为产生相同刺激条件信息量所对应的激励个数。由图3a可以看出，最大刺激条件信息为Issi=1.74 bits，对应此刺激条件信息的含噪语音信号的幅值范围为-0.97～-0.93 V。从图2已知此时平均互信息量I=1.414 bits，统计刺激条件信息Issi≥1.414bits所对应的幅值范围有-0.97～-0.86 V、-0.49～-0.13 V和1.05～1.12 V 3个区间。与不含噪声的语音刺激信号情况下的刺激条件信息图3b比较，可以看出加入噪声虽然使最大刺激条件信息量减少，但是刺激条件信息分布的空间增加了，因此加噪声后的平均互信息量也同时增加。图3中刺激条件信息分布反映了内部噪声在随机共振机制中所起的积极作用是一种统计意义下的平均信息增益，对于刺激信息个体的响应编码效率可能是负面的。

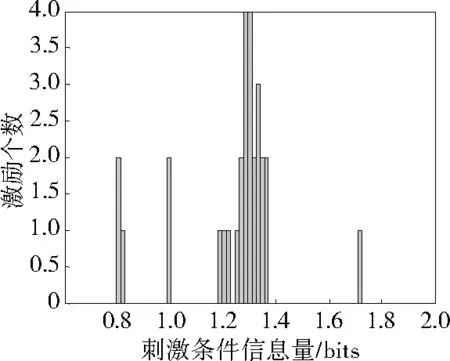
图4 N=50，σ=0.3(W/Hz)时的刺激条件信息量

图5 N=100，σ=0.3(W/Hz)时的刺激条件信息量

图6 神经网络的协同发放

在噪声强度为σ=0.3 W/Hz时，从图2可以看出，在我们所考虑的噪声强度下，神经元数N=50所对应的平均互信息大。图4和5分别表示了并联神经元数N=50和100对应的刺激信号所产生的刺激条件信息分布，可以看出，神经元数N=50所对应的刺激条件信息在1.2～1.4 bits区间也多于后者，因此对于刺激信号集合进行统计平均所得到的互信息量也会相对较大。所以，刺激条件信息分布能够更加细致地区分各刺激信号分量对于信息传输的贡献。同时，在此噪声强度σ=0.3 W/Hz下，图6给出了并联神经元数N=50的动作电位发放时间分布，横坐标为积分发放时间，纵坐标为神经元数目。由图6可知，在刺激信号和各个神经元内部噪声的作用下，膜电位从静息电位升高到阈值电位，导致动作电位的产生，特别是0.6ms时刻，几乎所有的神经元在噪声和语音信号的共同作用下进行了发放，使得神经网络在相应时刻达到协同积分发放。

3 结论

本文对于积分发放感知神经网络模型中的平均互信息量和刺激条件信息的计算方法进行了研究，对于不同数目耳蜗膜电位神经元的传输性能进行了分析。随着内部噪声强度的增加，平均互信息量的增加证实了神经网络中的超阈值随机共振现象，且在某些噪声环境中，有限数目的神经元就可提高传输效率。刺激条件信息分布的实验结果能够清晰地表示出最有编码效率的分量部分，不仅统计意义上给出平均互信息的大小，而且能够清晰地表明刺激信号中各分量的编码效率和内部噪声的可利用性。本文只是针对于并联神经网络做了初步研究，对于其他神经元系统如多层神经元网络或其他带有反馈环的复杂神经网络结构中，能否用刺激条件信息准确衡量刺激信号中各分量的编码效率值得深入研究。

[1]Borst A, Theunissen F E. Information theory and neural coding[J]. Nature Neuroscience， 1999, 2(11): 947-957.

[2]Arcas B A Y, Fairhall A L, Bialek W. What can a single neuron compute[J]. Advances in Neural Information Processing Systems， 2000, 13(1):75-81.

[3]DeWeese M R, Meister M. How to measure the information gained from one symbol[J]. Network: Computation in Neural Systems. Neural Syst, 1999, 10(4): 325-340.

[4]Butts D A. How much information is associated with a particular stimulus? [J]. Network: Computation in Neural Systems, 2003, 14: 177-187.

[5]Butts D A, Goldman M S. Tuning curves, neuronal variability and sensory coding[J]. PLOS Biology, 2006, 4(4): 639-646.

[6]Montgomery N, Wehr M. Auditory cortical neurons convey maximal stimulus-specific information at their best frequency[J]. The Journal of Neuroscience, 2010, 30(40): 13362-13366.

[7]Stocks N G. The application of suprathreshold stochastic resonance to cochlear implant coding[J]. Flucatuation and Noise Letters, 2002, 2(3): 169-181.

[8]Stocks N G. Suprathreshold stochastic resonance in multilevel threshold systems[J]. Physical Review Letters, 2000, 84(11): 2310-2313.

[9]祁明，许丽艳，季冰，等. 周期性语音信号传输的超阈值随机共振研究[J]. 复杂系统与复杂性科学，2013, 3(10): 31-36. Qi Ming, Xu Liyan, Ji Bing, et al. Suprathreshould stochastic resonance phenomenon of periodic voice signal transmission[J]. Complex Systems and Complexity Science, 2013, 3(10): 31-36.

[10] Chacron M J, Longtin A, Pakdaman K. Chaotic firing in the sinusoidally forced leaky integrate-and-fire model with threshold fatigue[J]. Physica D: Nonlinear Phenomena, 2004, 192(1/2): 138-160

[11] Barbi M, Chillemi S,Garbo A D. The leaky integrate-and-fire with noise: a useful tool to investigate SR[J]. Chaos, Solitons & Fractals, 2000, 11(12): 1849-1853.

[12] Cover T M, Thomas J A. Elements of Information Theory[M]. New York: Wiley, 1991:13-37.

[13] 杨一威，徐月晋，廖吉昌，等.人工耳蜗的膜电位积分放电刺激方案及其数字信号处理[J].南方医科大学学报，2012, 32 (10):1435-1439. Yang Yiwei, Xu Yuejin, Miu Jichang, et al. Digital signal processing of a novel neuron discharge model stimulation strategy for cochlear implants[J]. Journal of Southern Medical University, 2012, 32 (10):1435-1439.

[14]Yarrow S, Challis E, Series P. Fisher and Shannon inforamtion in finite neural populations[J]. Neural Computation, 2012, 24(7): 1740-1780.

(责任编辑 耿金花)

Study of Specific-Stimulus Information for Transmission of Speech Signals in Cochlea Neural Networks

WANG Fengjiao, REN Yuhao, ZHAO Jin, DUAN Fabing

(Institute of Complexity Science, Qingdao University, Qingdao 266071, China)

For decoding information contained in the cochlea neural networks responses to speech signals, it is interesting to address which parts of input stimuli are more efficient. In this paper, the stimulus-specific information associated with a particular stimulus will be adopted to study the decrease of average uncertainties, and its calculation method is developed. We use a leaky integrate-and-fire model to capture the responses of cochlea neurons to the input speech signal, and calculate the stimulus-specific information caused by each speech signal part. It is shown that the weighted average of stimulus-specific information over the stimulus ensembles yields the mutual information, and the stimulus-specific information is also useful in clearly indentifying the stimuli that are significantly efficient to the cochlea neural network. Moreover, the stimulus-specific information can not only determine which signal component mainly contributes to the mutual information, but also confirms the availability of internal noise in the neural networks. There is a non-monotonic relationship between the noise intensity and the maximum stimulus-specific information. These results indicate that the applicability of the integrate-and-fire neuron model for current cochlear implant decoding technology deserves to be further investigated.

cochlea neural network; speech signal; integrate-and-fire model; stimulus-specific information

1672-3813(2015)04-0104-05;

10.13306/j.1672-3813.2015.04.015

2014-12-25；

2015-05-11

山东省科技发展计划项目(2014GGX101031)

王风娇(1988-)，女，山东聊城人，硕士研究生，主要研究方向为信号处理与复杂性分析。

段法兵(1974-)，男，山东邹城人，博士，教授，主要研究方向为随机共振。

TN911.7；N945.12

A