涌现计算综述

李 劲， 肖人彬

(华中科技大学自动化学院，武汉 430074)

涌现计算综述

李 劲， 肖人彬

(华中科技大学自动化学院，武汉 430074)

从涌现现象入手，介绍了涌现计算的基本原理和特点；接着介绍了一种重要的涌现计算模型—元胞自动机，并阐明了涌现计算与群集智能的关系；然后探讨了涌现计算中待求解问题的涌现计算模型映射、自组织现象和同步现象等涌现计算中的若干关键问题；最后从工程涌现计算和社会涌现计算两个方面综述了涌现计算在自动设计，工程优化，交通管理、智能控制、信息处理等工程领域及其在公共管理、市场、经济和军事等社会领域的应用。

涌现计算；群集智能；元胞自动机

0 引言

在自然系统、社会系统以及许多人工系统中普遍存在着涌现现象。所谓涌现，是指由大量相对简单的单元(agent)构成的系统，在agent之间的局部相互作用下，会在整体上出现一些在局部观察不到的新的属性、规律或者模式。自然界中的很多物理现象，如大量气体分子共同作用产生气体压力，大量光子作用形成干涉或衍射图样，受激幅射产生激光等都可以视为一种涌现现象；在人类和动物社会系统中，蚂蚁的觅食、筑巢等行为，蜂群的花蜜采集行为，鸟群觅食和飞行行为，人类的交往合作行为等都是涌现现象；而在互联网、交通网、物流网络、经济系统等人工系统中也存在各种涌现现象。

人们构建了许多模型来模拟自然界中的涌现现象，如元胞自动机[1]、人工神经网络、人工生命模型，遗传算法、蚁群算法、蜂群算法、人工免疫算法等。此类模型具有一些共同的特征，那就是由多个相对简单的主体(agent)构成，每个agent遵守一些简单的规则并相互作用，从而在整体上产生涌现现象，具有整体大于部分之和的特点。通过将一些待解决的问题映射到此类模型中，可以对一些传统计算方法不易解决的问题进行高效的求解。这种利用涌现现象进行问题求解的方法称为涌现计算。

与主要关注于线性行为的传统计算方法不同，涌现计算是从非线性系统的涌现现象中获得计算结果的。在大量相互作用的简单单元构成的非线性系统中，存在自组织、合作、同步等复杂现象，对这些现象的研究有利于我们理解涌现现象的产生规律，从而更好地利用涌现计算来解决实际问题。在许多情境下，涌现计算具有比传统计算更高的效率，对于某些问题而言使用涌现计算方法是目前唯一有效的解决途径[2]。

1 涌现现象

1.1 涌现现象的基本概念和性质

涌现的一个简单描述性定义是：复杂系统内部个体之间通过局部相互作用，产生在系统层面上才能观察到的一些新属性和新现象[3]。在复杂系统中，随着系统从局部到整体的过渡，少数规则可以产生复杂而神奇的系统现象，在这些复杂的系统现象中存在一些特定的模式，我们通常将这些可识别并且可以重复发生的特征和模式称为涌现现象。因此可识别并且可以重复是涌现现象必不可少的特征之一，这意味着涌现现象反映着系统中某些规律性的部分。在孕育涌现现象的复杂系统中，通常不存在一个中心控制者，即涌现现象是在没有中心控制的情况下发生的，它基于众多主体的简单相互作用而产生，但同时又远远超过了主体个体的能力范围。由于无法从简单的局部规则中预测到会发生什么样的涌现现象，无法预料是涌现的另一重要特征，这一特性同时也带来了搜索和寻求问题更优解的可能性。

1.2 自然系统中的涌现现象

自然中存在许多涌现现象，这也是我们得以进行涌现计算建模的基础。一个典型的例子就是蚁群的觅食行为。每只单独的蚂蚁都是一个相对简单的个体，能力有限，只能完成一些简单的任务。然而，当大量的蚂蚁个体在一起形成蚁群时，整个蚁群就能表现出非常复杂和神奇的涌现现象，如社会分工、集体协作等等。例如在蚂蚁觅食的过程中，就能表现出具有智能的涌现行为，能够寻找到巢穴到食物的最优路径。这一行为已经超出了单个蚂蚁的能力范畴，是大量蚂蚁通过传递信息相互作用共同协作的结果。在蚂蚁觅食的过程中，不存在一个中心控制个体，蚁群是通过分布式的协作找到最快搬运路径的，这一行为完全是局部相互作用的结果，是蚁群中典型的涌现现象。除了觅食行为，蚁群中还存在劳动分工[4]和墓地构造[5]等涌现现象。与蚁群中类似的涌现现象在蜂群、鸟群和鱼群中同样存在。此外，人体中神经系统的记忆、学习等智能行为和表现可以视为神经元相互作用而产生的涌现现象[6]，大量细胞的相互作用中存在着丰富的涌现现象[7]。

1.3 社会系统中的涌现现象

涌现现象在人际交往，演员合作，科学家合作和经济系统等社会系统中非常普遍。

Tao Z等[8]提出了社区结构涌现的判别方法，并对美国安然公司以电子邮件发送关系形成的社会网络进行了研究，得到了社区结构的演化过程及其涌现现象的计算结果。

此外，经济系统也是一个很好的例子。随着计算机技术的发展，研究者们越来越多地使用多agent涌现合作系统来对市场互动行为进行探索，以发现经济金融现象中更多的规律和知识，为价格预测，资产交易及市场应用设计新的商业模式。经济学之父亚当·斯密曾提出有“看不见的手”在引导着市场，今天我们可以认为这个“看不见的手”其实是经济领域的涌现现象，可以由涌现计算模型和算法进行预测。智能涌现计算与经济学的交叉将有利于更好地洞察人类市场互动行为的本质[9]。

1.4 人工系统中的涌现现象

通信网、交通网等许多人工构建的系统中也存在着涌现现象[10-14]。比如计算机网络中数据包传输的拥塞现象，交通系统中的交通堵塞，人工多主体模型表现出来的与生物启发原型相似的各种涌现行为等。

Christie P[15-16]等对人为建造的复杂系统—计算机网络的涌现特性进行了研究，他们用分数维描述了计算机互联网的涌现集群特性，对最短连线问题进行了研究，定义维度的倒数为几何温度Ti，分析表明系统在Ti约为0.5时会发生相变。而以计算机网络为平台，还诞生了类似BitTorrent的分布式系统，虽不存在中心控制，看似处于“无政府状态”，但系统运作良好且具有很好的鲁棒性，其工作过程中存在大量涌现现象值得研究和借鉴。

在图象数据库这样的人工系统中亦存在涌现现象。Santini S等[17]发现在图象数据库中特定图像的语义是一种涌现现象。他们认为图像本身并不具有固有的内在含义，而是将它们置于由其他图像构成的上下文环境中并在用户互动中涌现产生的，并据此提出了一种图像操作与配置接口模型，使得用户不但可以对单个图像进行操作也可以对图像之间的关系进行操作和定义，从而让图像可以在互动中产生涌现语义。

人为构建的机器人系统中亦存在涌现现象，可以利用其进行机器人的智能化控制。Shimizu M等[18]对一种名为Slimebot的机器人系统进行了研究，这个系统由多个相同的模块化的小机器人组成，根据环境的不同在分布式算法的控制下相互作用组成不同的形态。实验表明，在基于涌现现象的算法作用下，可以在保证系统连贯性的情况下对机器人的形态进行实时控制。Lee S I等[19]开发了一种基于遗传算法的模糊逻辑控制器用于控制移动机器人，并用内部模型的状态转换图分析了控制器的行为。实验结果表示通过进化可以获得恰当的控制策略，并且在所获得的模糊规则集的互相作用下，机器人会表现出涌现行为。

硬件技术的发展使构建大规模的无线传感器网络成为可能，单个传感器体积大大减小，功耗降低，价格也越来越便宜。在大量智能微终端构成的智能微尘中多个传感器之间的局部作用会产生通信与合作，节点失效与网络的鲁棒性等许多涌现现象值得进行深入的研究[20-22]。

对于人工系统中的涌现现象进行研究，一方面可以更加了解系统的运作方式和演化动力学过程；一方面可以运用涌现现象中存在的规律，对系统进行控制和优化，提升系统的性能。

2 涌现计算概述

2.1 涌现计算与涌现现象之间的关系，涌现计算的基本定义和特点

在自然系统、社会系统和人工系统中，普遍存在着涌现现象[23]。可以通过多主体的方法来对这些系统及其中存在的涌现现象进行摸拟。例如蚁群、蜂群、鸟群及菌落等生物系统中便存在聚集，迁移，合作觅食等众多涌现行为和现象，可以使用计算机对其进行模拟[24-26]。对蚁群的模拟导致了蚁群算法的产生，对蜂群的模拟则是构建蜂群算法的基础。具有类似的合作觅食行为的群体称为社会觅食昆虫，它们可抽象为一种多主体系统，要实现合作觅食，需要群体在具有内部凝聚力的同时对环境刺激保持恰当的响应。Liu Y F等[27]将凝聚力表征为一种稳定属性使得即使在系统中存在因检测其他主体位置和速度以及食物源的位置时存在的不确定性而带来的噪声情况下，局部主体的行为依然可以在整体上涌现出合作觅食的行为。他们的实验结果定量证实了在某种意义上合作觅食优于个体觅食，并明晰了局体主体的相互作用和群体涌现行为之间的联系。仿真模型在实验中表现出了复杂而有序的群体行为，与真实的生物群体在噪声环境中表现出的行为非常相似。

同时需要注意到的是，一方面，涌现出来的现象并不一定总是我们所期望的，比如在神经系统中，癫痫症状也是一种大量神经元相互作用下的涌现行为[28]，但并不是我们所期望的，反而是需要想办法消除的；另一方面，所需要求解的问题并不一定总具有显式的多主体结构。因此，涌现现象或对涌现现象的模拟并不完全等同于涌现计算。为了利用涌现现象对问题进行求解，首先需要对自然中存在的某些复杂系统及涌现现象进行抽象并建立相应的多主体模型；接下来需要对模型的特性进行研究并对其进行修正和控制，以使其可以产生所需要的涌现现象与模式；最后，对于某个具体的待求解的问题，需要将它映射到某一种建立好的多主体模型中，这样才可能利用多主体系统的涌现现象对问题进行求解，这个过程便是涌现计算。涌现计算具有去中心化，并行运算的特点，而且具有黑箱特性，往往不需要对所求解问题进行精确的数学建模，在许多复杂问题的求解上具有一定优势。

值得注意的是，虽然涌现计算是一种“自底向上”的算法，一定的局部规则会产生什么样的涌现现象往往难以预测，而近年这一问题更具难度的逆问题——即给定一个期望产生的涌现现象，那么系统中的主体应该遵循什么样的局部规则才会导致这一特定涌现现象的产生—也得到了注意和研究[29-31]。这将有利于增加我们对涌现现象的认识深度和控制能力，具有一定的实用价值。

综上，我们可以认为涌现计算是由一系列独立计算处理进程并行合作构成的计算过程的总体，由低等级计算进程之间依照特定规则集进行相互作用而构成高等级计算过程，实现可预计的总体功能，不受任何形式的全局控制，以局部作用产生的涌现现象作为计算结果，并能够在演化过程中实现自身稳定和收敛。

图灵机数学模型奠定了现代计算机科学的理论基础，它使用一个读写头进行工作，每个时刻只完成一步操作。以图灵机为基本模型的传统计算模式也多采用串行的工作模式，虽然在原则上能够模拟一切运算，但是在遇到类似NP难问题这样复杂度很高的问题时，由于求解时间随问题规模快速增长，实际的计算求解变得不再可行。与大多数传统计算模式的串行工作方式不同，涌现计算采用分布式的并行运算模式，且在涌现计算中不存在中心控制，而主要依赖个体之间的局部作用来在整体上涌现出计算结果，这些特点使得涌现计算模式能够在可接受的时间内为一些无法使用传统计算模式求解的问题提供可接受的解。因此，涌现计算是传统计算模式很好的补充，为计算问题提供了一种新的求解方法和途径。

2.2 一种涌现计算模型：元胞自动机

元胞自动机(亦称为细胞自动机)是一种离散模型，最早由冯·诺依曼在1950年为模拟生物细胞的自我复制而提出。此后，S.Wolfram对初等元胞机256种规则所产生的模型进行了深入研究，并用熵来描述其演化行为，将元胞自动机分为平稳型、周期型、混沌型和复杂型。

一个标准的元胞自动机(A)由元胞、元胞状态、邻域和状态更新规则构成。可用式(1)来表示

A=(L,d,S,N,f)

(1)

其中，L为元胞空间；d为元胞自动机内元胞空间的维数；S为元胞有限的、离散的状态集合；N为某个邻域内所有元胞的集合；f为局部映射或局部规则。

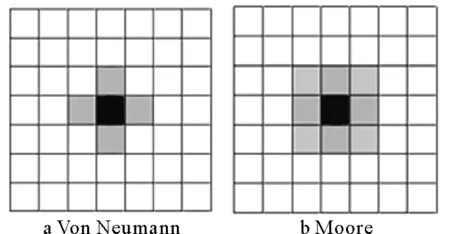
图1 传统元胞自动机的邻域定义方式

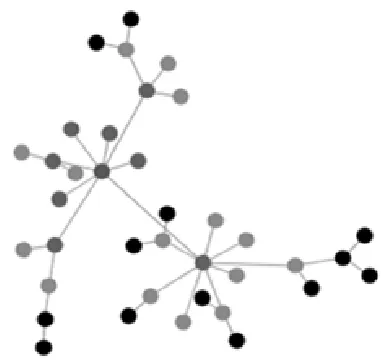
图2 基于网络的元胞邻域定义

元胞空间是元胞所分布的空间网点的集合。传统元胞自动机的邻域定义方式有Von Neumann邻近和Moore型邻近两种，如图1所示。近来则发展出了类似于网络连接的邻居定义方式，如图2所示，这样元胞的邻居将不被限定于其位置的附近，从而在很大程度上拓展了其结构复杂性，可能产生更复杂多样的涌现现象，具有更强的信息处理、问题表征和求解的能力。如宋玉蓉、蒋国平突破了元胞自动机的传统邻域定义方式，采用网络的邻接矩阵A直接定义各元胞邻居关系，从而可以使用元胞自动机模型对诸如Internet,WWW, P2P 和E-mail 等信息技术网络中节点交互具有全局特性的对象进行仿真研究[32]。理论上元胞空间在各个维向上是无限延伸的，为能够在计算机上实现定义了边界条件，包括周期型、反射型和定值型。

一个元胞通常在一个时刻只有取自一个有限集合的一种状态，例如{0,1}。元胞状态可以代表个体的态度，特征，行为等。在空间上与元胞相邻的细胞称为邻元，所有邻元组成邻域。

元胞自动机是一种涌现计算的统一框架，它是一种由在局部转化规则控制下逐代进化的细胞阵列构成的离散系统。很多涌现计算的仿真研究都借助了元胞自动机方法，因为元胞自动机是一个具有简单构造但产生复杂自组织行为的离散动力学系统，它能够有效地克服平均场方法建立的微分方程模型因只能反映同步行为的平均趋势而只适合对同步行为作整体预测的局限性，也能克服基于马氏链建立的随机模型缺乏空间概念、模型复杂、不适合描述同步行为动态演化的特征。由于这种通用性，元胞自动机模型在涌现计算的诸多不同领域得到了广泛应用。Simons N R S等[33]利用元胞自动机来描述二维电磁场问题，并对一维平面波在理想矩形波导柱中的传播与反射进行了求解。Mamei M, Roli A等[34]对受扰动的细胞自动机进行了研究，发现在系统不受扰动时某些特定行为并不会涌现出来，此类宏观行为常在普适计算中涌现，值得进一步研究、控制和利用。

作为一种计算模型，元胞自动机可以在普通计算机上实现，也可以使用专用的电路实现。它已被证明是一高效的VLSI(超大规模集成电路)体系结构。量子元胞自动机是一种具有很好前景的涌现技术的纳米电路实现，它具有很高的集成度、切换频率和很低的功耗。元胞自动机的量子元胞自动机实现，不仅推动已开发出来的元胞自动机系统向纳米时代升级，同时也大大提高了其性能[35]。这为涌现计算的实现提供了更强有力的计算平台。

涌现计算的确定和元胞自动机的通用性问题在过去三十年里得到了很好的解决，而在计算机科学和非线性科学的边界上，神奇的涌现现象会在哪里出现这一问题至今还有待进一步探索。Sapin E等[36]提出未来的工作可以对所有已发现的元胞自动机进行评估，计算出Langtons lamda等规则参数。以所有实现“与门”功能的元胞自动机为例，它们可能有相似的参数值，这也许可以回答计算通用性的边界在哪里，有助于更好地理解局部规则作用下复杂系统中的涌现计算。

2.3 涌现计算与群集智能

群集智能是指众多行为简单的个体相互作用过程中涌现产生的整体智能行为。群集智能模型使用一组相互之间可以进行直接通信或者间接通信的主体合作进行分布式的问题求解。蚁群算法便是群集智能的典型代表之一。此外，根据蚁群的劳动分工和墓地构造等现象提出的一系列模型和算法，以及Kennedy 等[36]通过观察鸟群的协作觅食活动开发的粒子群优化方法(Particle Swarm Optimization, PSO) 也都属于群集智能的范畴。目前群集智能包括蚁群优化方法ACO和粒子群优化方法PSO两个大类，主要用于复杂问题求解。智能行为可以认为是多个主体互动而产生的一种涌现现象。群集智能正是简单的主体通过交互作用所表现出的不可预见的宏观智能行为的特性，这种群体层面表现出的智能行为是一种涌现现象，因此群集智能属于涌现计算范畴，是涌现计算中重要的组成部分。可以认为涌现计算是一种产生群集智能的重要途径和方法。目前，群集智能的建模工具包括动力学建模、元胞自动机、人工神经网络、遗传算法、蚁群算法和粒子群算法等[37]。它们亦都属于涌现计算的具体实现算法。

3 涌现计算中的若干关键问题

涌现计算中存在涌现模型映射、自组织、同步等关键问题，这些问题之间互相交叠，相互关联，共同影响着涌现计算的过程和结果。

3.1 向涌现计算模型的映射

目前常用的涌现计算模型有元胞自动机、蚂蚁算法、蜂群算法、神经网络、遗传算法等。在进行具体问题的求解时，首先需要做的就是要完成从具体问题到涌现计算模型的映射。要将需求解的问题和条件在涌现计算模型中表达出来，并进行相关的定义以便对计算所得到的涌现结果进行解释和翻译，转化为实际问题的解。

以元胞自动机为例，在求解工程设计中的连续结构拓扑优化问题时，便需要建立元胞自动机和结构有限元之间的映射关系，以利用元胞自动机完成连续结构涌现计算[38]。文献[38]中所提到的连续结构拓扑优化是在设计空间、支撑与载荷条件和某些工艺设计等受限条件下，确定结构构件之间的相互连接方式，结构内有无孔洞、孔洞的数量、位置等拓扑形式，使结构能将外载荷传递到支座，同时使结构的某些性能指标达到最优。在使用元胞自动机模型进行涌现计算求解时，首先要用规则形状的单元进行连续结构的网格划分，然后用有限元方法计算在给定载荷和约束条件下的局部应变能密度，再将上述网格映射为元胞自动机的进化环境，然后要利用“比例—积分—微分”控制原理和满应力设计准则重构基于应变能的元胞局部进化规则，通过元胞进化得到单元密度变化系数，从而得到新的设计域，重复上述过程直到进化出满足收敛条件的连续结构的拓扑形式。

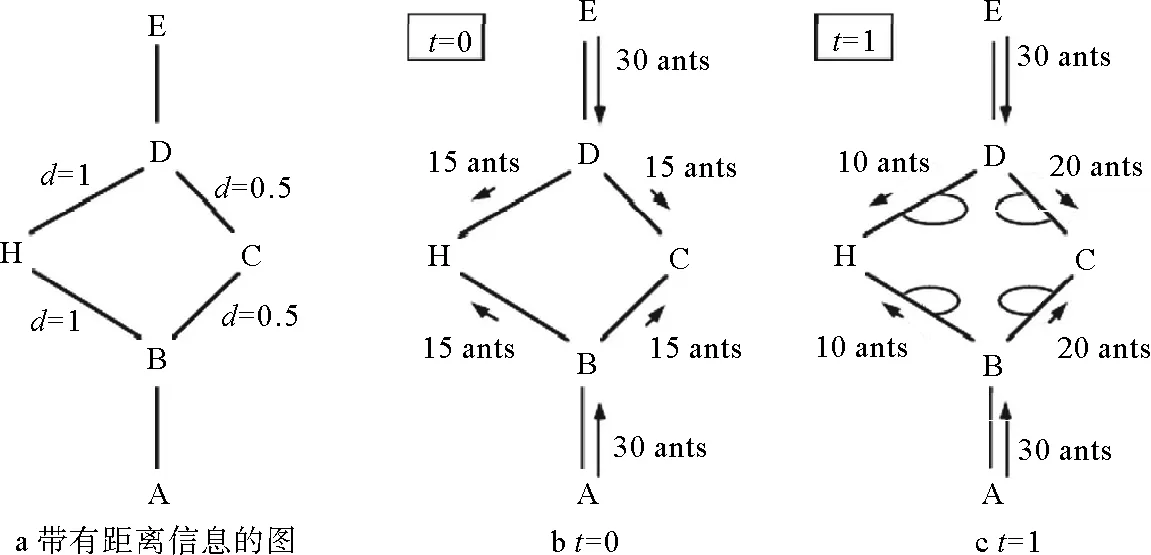
图3 利用蚂蚁算法模型进行路径求解的原理示意图

又例如，当使用蚂蚁算法求解旅行商问题(Traveling Salesman Problem, TSP)时，首先需要将城镇映射为蚂蚁算法中的图的结点，将城镇之间的路程映射为结点之间的连接权。假设在初始状态，所有蚂蚁被放在不同的节点上，每只蚂蚁路由表的第一项是其起始节点。每只蚂蚁按某种算法根据信息素和距离信息以一定概率选择一个目的结节并向其移动，当迭代进行到一定程度时，所有蚂蚁都完成了旅行，他们的路由表会被装满，这时对每只蚂蚁的路由信息以某种方式进行评估可以得到一条生成的最短路径。这个过程可反复执行直到达到最大次数限制或所有蚂蚁都使用同一路径的时候。其求解最短路径的示意图如图3所示。这样便利用蚂蚁算法模型涌现计算得到了TSP问题的解[39]。

对所求解问题进行涌现计算模型的映射，要求设计者熟悉所求解问题的结构，同时了解涌现计算模型的结构和计算特点，在计算前需要对问题进行表征，并在获得涌现计算的结果后对其进行解释和转化。涌现计算模型中各个构建的属性、它们所处的环境及它们之间作用规则所代表的意义都是人工指定的，这需要人工参与涌现计算的过程，并且对于每一个具体的问题都需要设计一个独特的涌现计算模型。而我们知道，生物神经系统在进行信息处理时具有某种通用性，类似于一个“黑箱”系统，构成涌现计算系统的神经元和它们之间的作用规则是相对独立的，并不受外部环境的直接影响，这样一个系统仅通过传感系统和执行系统与外界进行交互，从某种程度上来说人类的神经系统是一个具有通用性的涌现计算系统。借鉴脑科学的研究成果，也发展出了类似的涌现计算模型。

如Juyang Weng等[40]就构建了这样一种模型，它由感知器、启发式代理和执行器构成，其结构如图4所示。启发式代理由一些相互之间在启发式算法下相互作用的单元构成，与使用符号表征时处理单元内部环境对外部环境是开放的不同，它们被限定在一个相对独立的内部环境的结构中，与外界环境之间由一个被称为“头盖骨”的结构相互隔离，仅通过感知器和执行器与外部环境进行交互进行涌现表征和计算。启发式代理在“出生”后能不需要人工直接对其进行定义和修改，通过交互式的学习来获得针对各种不同任务的技能，所以不必针对每一个具体任务进行映射，具有一定通用性。

图4 一种涌现计算模型

3.2 自组织

自组织是指某一系统中自发形成的时空有序结构或状态。它是一种在没有中心控制(没有组织者或其他系统之外的设计)、没有完全信息的条件下，仅仅通过微观个体的局部相互作用导致的系统全局结构的涌现。自下而上、自发性、涌现性是自组织必备的和重要的特征。自组织有3个主要特性：涌现、自适应、进化。涌现是一种由系统各组元之间的相互作用而形成的全局现象。适应性自组织系统通过自下而上的涌现行为处理干扰的存在和对环境变化作出自动的适应性改变以维护系统的稳定。进化是自组织系统涌现和适应性综合作用的结果。自组织现象在自然与人工系统中普遍存在。

自组织是一个自发产生的从无组织(或欠组织)到有组织的过程，对应着系统的有序度的增加[41]，这使得系统能够获得时间、空间或功能上的结构以适应环境，所获得的这种适应性结构便可视为涌现计算得到的解。涌现计算利用了自组织的适应性，但有序度的过度增加则意味着系统的僵化和环境适应性的下降[42]，因此在涌现计算中系统的有序度应该维持在一定范围。有序度过低则无法表现出适应性，对应着计算无法收敛得到有效的解；而过高则表现出僵化特性无法再对新的输入作出反应，涌现计算中的“早熟”现象便是有序度过高的表现。因此涌现计算中的自组织应在有轶序与混沌之间取得平衡，即处于混沌的边缘。这时系统将同时具有有效结构和环境适应性。

那么自组织会在什么样的条件下发生，又是如何发生的呢？Nicolis G 等[43]认为自组织发生在由非线性相互作用的元素组成的远离平衡态开放系统中，这意味着为涌现计算而构建的人工系统是由互相之间具有非线性作用的多个元素构成并且处于远离平衡态的混沌的边缘。Nicolis G 等给出的为必要条件，相对宽泛，因为并不是所有非线性作用都能产生自组织现象。Haken[44]则进一步指出自组织中非线性作用的具体形式为竞争性协同，即涌现计算系统中的多个主体之间同时存在竞争与合作的关系。我们认为系统开放并远离平衡态是自组织的必要条件，涌现计算系统开放于求解环境中进行输入物质、能量和信息的交换，系统中各主体在竞争性协同中实现正反馈机制，使系统中蕴含的有序性得到增强与表达，进而自组织形成某种特定的功能性结构，从而涌现出所求解问题的解。

涌现计算的计算结果作为一种涌现现象，本身也是自组织的产物，计算结果的合理性和可用性表现出自组织过程对于外界环境的适应性，而得到这一结果的过程即是系统自组织进化的过程。因此作为复杂系统中的重要基本特征，自组织也是涌现计算中的关键问题之一，涌现计算中的自组织得到了很多研究和关注。Liu J M等[45]提出“面向自治的计算”，侧重对复杂系统中实体中的自治行为建模及它们在达成某一个特定目标过程中的自组织现象进行研究。社会系统的子系统之一——供应链系统中，多企业主体在开放结构下会在非线性互动中自组织涌现出供应链协作结构和模式。李健，李刚等[46]采用多代理技术仿真对分散化供应链中的自组织演化机制进行了研究，研究表明演化对初始条件高度敏感，受外部环境和企业内部机制因素控制，并存在着锁定、路径依赖和混沌等自组织系统特性。顾珊珊等[47]将车辆和信号灯视为主体，用元胞自动机模拟动态交通流，在激励学习方法和遗传算法的作用下，交通系统可以涌现出一定的动态特征和规律，实现自组织控制。张嗣瀛[48]对自组织和自聚集现象进行了研究，并给出了一个表达式对相关的规律性现象进行概括与解释，指出此式的多次重复对应着重复的聚集和组织过程，是形成一类复杂系统结构的基本规则。

3.3 同步

罗吉贵等[49]认为，构成复杂系统的基本单元都按照某种动力学规律随时间演化。由于基本单元之间存在相互作用，所以它们的演化并不是孤立的，而是在任何一个固定时刻的动力学性质表现出某种依赖关系，这种依赖关系即是同步。涌现计算的结果是复杂系统涌现出来的一种特征模式，可以视为复杂系统的斑图，其反映了系统经自组织过程而形成的某种有序性的结构。在计算过程中，构成计算模型的基本单元按照某种动力学规律演化，它们之间按局部规则进行相互作用，这使得它们的演化不是孤立的，动力学性质表现出某种依赖关系，即为同步关系。而斑图正是同步关系在宏观尺度上的表现，多样化的同步导致了涌现现象即涌现计算结果的产生。因此涌现计算的基础——涌现现象正是由同步种类的多样性，尤其是广义同步的存在而产生的，同步现象的研究对于涌现计算有着重要的意义。

同步现象是复杂系统中最早得到研究的问题之一。Winfree和Kuramoto分别提出了Winfree 模型和Kuramoto 模型，假定系统中每个个体具有相同的振动周期，将同步问题转化为相同步问题进行研究[50-51]。2000年，Néda 等[52]研究了人群中的掌声同步现象，通过对音乐厅里录制的真实掌声进行分析，得出掌声同步时周期加倍的结论，并借助Kuramoto模型进行了理论解释[53]。李德毅等[54]选取“掌声响起来”作为初始状态，以心理学中的“从众心理”为基础，利用认知物理学中的云模型和数据场理论构造了一个描述集体行为的非线性涌现模型，开发了涌现计算实验平台，对音乐厅里掌声的自发涌现机理进行了分析并模拟了多样化的掌声同步的虚拟现实；进一步，他们将听众群体视为一个复杂多代理网络，分析了掌声涌现同步的内在关键因素，探讨了领掌者如何影响涌现掌声同步，领掌者分布的影响等问题，指出掌声的涌现同步有路径多样化，不确定性和适应性，掌声同步研究所用的模型和方法也可为其他局部信息和局部控制下的复杂多主体网络的集体行为研究提供借鉴[55]。同步现象在自然界的复杂系统中广泛存在，比如在视觉皮层中便发现了长程同步现象，受此启发，DeLiang Wang[56]提出了一种局部耦合神经振荡器模型，它可以涌现出与视皮层类似的全局同步现象，在知觉编组和模式划分上具有全局连接神经网络模型所不具有的一些优势。Zhang Q J 等[57]考察带有延迟结点的复杂动态网络，对适应性反馈同步进行了研究发现了全局指数同步的一些新条件，并进行了仿真验证。对复杂网络中的混沌同步进行了研究，由理论分析通过数值仿真提出和验证了同步产生的条件，并指出当耦合配置和内部耦合矩阵满足特定条件时，混沌同步是不可能实现的[58]。能够正确获知复杂系统中同步行为的发生对于自然及人工涌现现象的建模和研究具有深远的意义，Boulden S 等[59]在各种复杂网络拓扑上运行空间迭代囚徒困境并采用遗传算法进行了涌现行为的获知，结果显示仅有策略代价信息是不够的，需要更多的信息来对同步行为进行感知。

对于涌现、自组织和同步等复杂系统中关键主题的研究，将能够帮助我们更好地认识涌现现象发生的机理，从而控制涌现现象的产生和发展的方向，有利于在涌现计算中避免不需要或不希望的涌现现象的产生，获得所需要的涌现现象，使涌现计算的过程更具可控性，提高涌现计算求解问题的能力。

4 涌现计算的典型应用

4.1 工程系统中的涌现计算

许多涉及到众多影响因素的复杂工程问题往往可以使用涌现计算得到很好的解决。

肖人彬等[38]采用基于元胞自动机的连续结构涌现模型计算了在不同温度边界条件和热源分布情况下方形平板散热的最优拓扑结构，实现了基于涌现计算的自动结构设计，实验证明这是一种有效而高效的设计方法。汪镭等[60-62]将涌现计算中的一种重要算法模型——人工神经网络应用于自动控制及传动系统领域，取得了良好的效果，此外他们还以反馈式神经网络和群体智能算法为基础给出了自然计算理念统一的框架描述, 自然计算领域内的相关群体智能算法表现出一种相对统一的智能计算模式，即涌现计算模式。

Dong J 等[63]报道了一种基于局部信息的交通分配(dynamic traffic assignment, DTA)模型，仅使用由地下传感器收集的局部信息而非全局信息来做出通行和限制通行的决策。与其他DTA算法的仿真比较实验证明，这种算法具有鲁棒性和高效性。在智能交通中亦使用到了涌现合作技术[64]。

涌现计算在智能控制系统中扮演着重要的角色。在复杂动态系统的控制中，出现了越来越多的传统控制理论所不能满足的需求。这主要是由于问题的复杂性和环境的不确定性常常需要使用启发式推理对以往的经验进行学习从而进行与人类相似的决策。这时系统要通过学习积累关于问题的信息动态地产生可接受的解。使用神经网络、模糊逻辑、遗传算法等涌现计算方法可实现这样的功能，它们经常与传统控制理论一起被用于构建高性能的智能控制器[65]。在生产控制领域，传统的中心控制连续信息处理方法也逐渐不能满足快速变化的生产环境的需要，对于计算复杂、非线性和不确定的环境，亦需要使用基于涌现的多主体分布式智能控制方法[66]。

Arena P 等[67]将涌现计算用于有腿机器人的运动控制，通过使用模拟细胞神经网络的自组织涌现结果生成运动步法，并使用VLSI实现了基于模拟细胞神经网络的中枢模式发生器，实验结果证明了这种方法的适用性。在过去几十年里，有腿机器人的高速动态步伐得到了许多研究，但目前发表的研究从生物力学和工程角度上来说都未能充分地描述高速奔跑的动力学特征并实现它。Krasny D P等[68]使用一种称为基于集的随机优化的高效进化算法来产生高速的步态。这个算法可以找到用来生成周期性轨迹的开环控制参数。测试了多种方法用来生成腿的周期轨迹，结合进化搜索找到的联合方案，实现了绞链连接的四足机器人在非均匀负重情况下的节能、自然和非受限的快速奔跑，出于比较目的，同时也实现了跳跃和慢跑。实验表明在最高可达10m/s的速度范围内实现了基础步态显示出来的涌现特性。这个模型可以实现在动物身上观察到的主要动力学特征。在结构简单的机器人系统上也可以实现自然高效的移动。涌现计算在认知机器人中的应用尤为引人注目。Paolo Arena等[69]基于生物启发计算算法的时空非线性神经阵列，使用简单的距离、接触和视觉传感器作为输入，让机器人基于用例进行认知学习并产生能针对特定目标的涌现行为，其系统结构如图5所示。机器人可以自行通过认知过程涌现出完成某一目标的解决方案，并在简单传感器所获取的外部信息诱导下对外部环境产生响应完成特定任务，图6展示了机器人的结构及其自动生成的运动路径。这种方法让机器人可以处理事先不可预知的动态变化的环境，而这在太空任务或我们的日常生活中都是非常常见的。

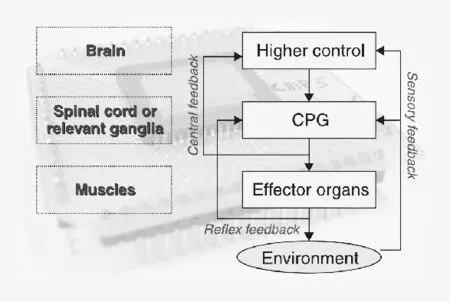
图5 带有传感反馈的机器人系统框图

图6 机器人的结构及其自动涌现生成的运动路径

Floreano D等[70]使用一个时间离散的迭代神经网络进化算法控制一个实体的移动机器人，通过在实验初期设置的一组约束条件，在无需预先进行设定的情况下，机器人自动涌现出了对电池充电器进行定位并周期性回到充电器所在处进行充电的行为。

Yong Li等[71]提出了一种正反馈HOPFIELD神经网络结构，具有类似于标准HOPFIELD方法的涌现特性，用于交叉开关切换控制，相比于包括标准HOPFIELD方法在内的以前的方法，在计算时间和解的质量上均具有优势。

除用于智能控制外，涌现计算还可应用于语音和图像信息处理[72]。杨淑莹等[73]使用免疫猫群优化算法实现了不依赖于初始码书选取，鲁棒性强且低语音识别误差率的矢量量化码书设计。基于涌现计算的多核和结构可重构平台不断发展，视觉处理系统变得越来越复杂，性能也更加强大[74]。模仿人脑工作模式的涌现时域处理技术可用类似人脑的方式进行视频识别和文本处理。Weng J Y 等[40]的模型借鉴脑生理的研究成果，由感知器、启发式代理和执行器构成，其结构如图7所示。有别于面向任务的内部符号表征方法，它采用启发式网络,通过感知器和执行器与外部环境的交互自动进行涌现表征。启发式代理被认为限定在一个类似“头盖骨”的结构中不受外界环境的直接影响，形成一个相对独立的内部环境，仅通过感知器和执行器与外部环境进行交互。启发式代理在“出生”后能在不需要人来重新进行启发式程序的编程或直接对其进行修改的情况下通过增量学习获得针对各种不同任务的技能。

在智能房屋领域，涌现计算被用来进行电力规划与决策。带有发电储存和交易功能的智能房屋不再只是电网中一个无源的负载，而是有双向的能量流入与流出。将智能房屋视为主体，可使用基于多主体的方法，结合当前和预期的用电量、发电量和贮电量来自动决定买入、存储或是卖出电力资源，从而最小化其电费账单[75]。

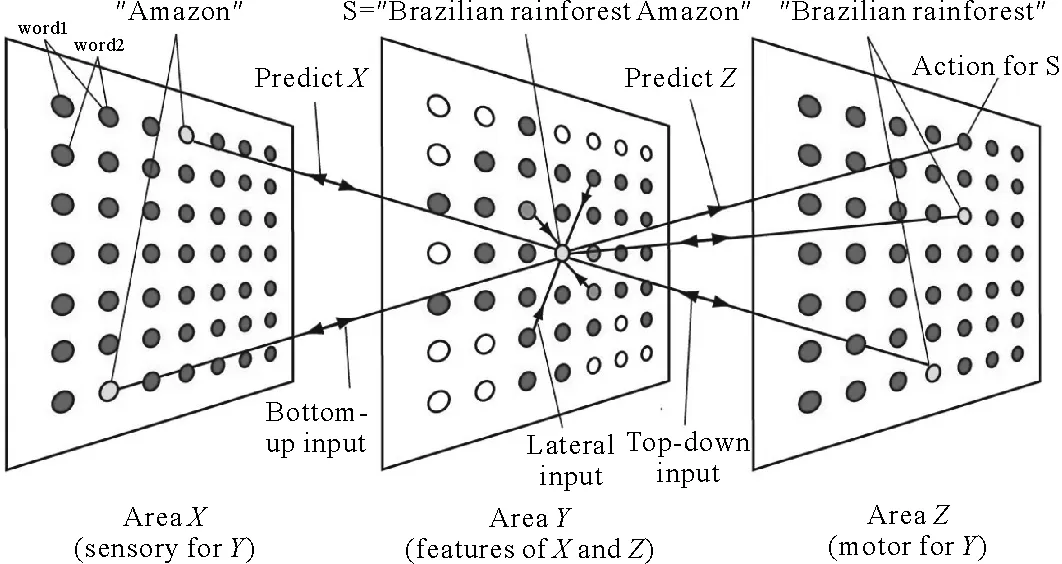
图7 感知器、启发式代理和执行器结构模型

当然，涌现计算并不一定都是在计算机上完成的。日本北海道大学的Tero 教授等[76]利用粘菌进行涌现计算设计了一张连通东京及其附近城市的铁路网。粘菌是一群裸露的无细胞壁多核的原生质团，它们可以通过连续的形变而缓慢移动，当这团裸露的细胞在空间上遇到多个分散的食物源时，就会构建起一些运输营养的通道。Tero教授等将一张东京以及附近城市的地图作为粘菌生长的环境，在初始时刻，让粘菌集中在地图上的东京点，接着在地图东京附近的城市放上粘菌喜欢吃的食物，然后让这群粘菌在实验地图上缓慢变形、游走。经过一天多的时间，它们演化出了一张与现实的东京附近的地铁网络在结构与形状上均非常相似的营养运输网络，如图8所示。也就是说，使用粘菌进行涌现计算完成了复杂而高效的轨道网络运输系统的优化设计工作。

4.2 社会系统中的涌现计算

在市场与经济系统[77-78]，社会技术系统[79]，科学与教育[80]、演艺圈、人际关系社团[81-82]等社会系统中存在着大量的涌现现象，亦可以使用涌现计算来解决其中的很多问题。

Izumi K等[83]提出了一种人工市场方法，用基于主体的方法来进行外汇市场的研究。用这种方法可以解释市场中的峰值和重尾等涌现现象。通过采访和问卷的方式来收集行业数据。调查显示经销商在学习中的互动与生物中的基因操作比较类似。使用基因算法建立了一个人工市场模型。这是一个由具有市场状态内部表征的agent组成的多agent系统。然后结合基本经济因素和政治新闻的真实数据集进行了仿真。识别到了市场中的3个涌现现象，并推论这些涌现现象可以由因代理个体预测互动和市场供需平衡形成的预测多样性的相变来解释。实际领域数据支持了仿真的结果。这种方法整合了实际工作与多代理模型，提供了市场中微观与宏观联系的定量解释。栾笑天等[84]使用元胞自动机设计航空物流市场的演化模型，得到了航空物流市场的演化阶段与细分市场特征的模拟结果，其模型能够有效模拟各物流细分市场受不同阶段影响因素的敏感度。Koritarov V S[85]使用计算社会学中基于主体的建模与仿真方法(Agent-Based Modeling and Simulation, ABMS)将电力市场作为一个复杂自适应系统进行了模拟与分析。这个仿真模型由代表电力市场中参与者的主体、代表主体存在和相互作用环境的互动层以及代表时间层的计划周期构成。通过此模型可以有效地研究物理基础设施(如发电站，电力传输系统等)和市场参与者的经济行为之间的复杂互动行为。此外，涌现计算方法还被用来对电力客户进行分类[86]。龚小庆等[87-89]探讨了固定环境中的稳态涌现；对复杂系统在演化过程中所涌现出来的一种统计规律—Zipf律进行了研究，证实了Zipf律与幂律分布的统计等价性；他们还从复杂系统的角度对经济系统进行了研究，指出经济系统是一个具有分形特征的多层次的规则耦合关系网，其演化具有断续平衡和路径依赖的特征，经济系统中生态位的重叠导致外部性的产生，而制度的涌现和演化过程就是外部性的产生、转换和平衡过程，这些关于经济系统中涌现现象的研究为涌现计算在经济领域中的应用提供了理论支持。赵剑冬等[90]基于Agent的经济社会系统建模与仿真研究进行了一种使用涌现计算方法ABMS研究经济系统的新尝试，其建立的计算机仿真模型可以帮助分析影响产业集群发展的多个因素。

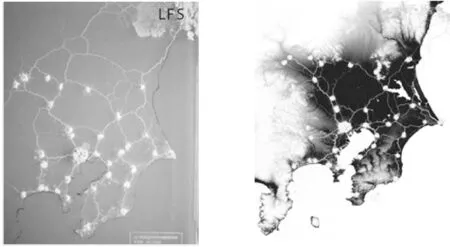
图8 粘菌涌现计算结果与东京周边铁路网络的对比图

除经济系统外，涌现计算亦可用于军事决策支持。计算红军(CRT)是一种基于仿真的优化应用，用以发现军事策略(或工作计划)中的不足之处。CRT的目的在于识别出那些表现出感兴趣涌现现象的仿真模型。在CRT中使用的是海量多主体进化算法。由于传统CRT所使用的基于帕累托的算法会收敛于帕累托最优，次优的替代策略会被遗漏，从决策者的立场这限制了CRT的应用，Zeng F C等[91]通过在海量多主体进化算法中使用多样化强化策略，有效提高解决多样化问题的能力，增强了CRT用于辅助决策的能力。

对于大学课程时间表这样人们所熟知的复杂规划问题，亦可以使用涌现计算对其进行求解。Lewis R等[92]提出了一种衡量种群多样性和个体距离的方法，通过引入大量不同的适应度函数，使用附加的局部搜索操作符对使用群基因算法进行了改进，用以求解上述问题取得了较好的效果。

针对更一般性的社会学命题，王飞跃等[93]采用人工社会模型，基于代理的建模、模拟和分析来进行研究，指出通过涌现的方式，人工社会模型中可以方便地涌现出合作、调节、反馈、竞争、冲突等复杂系统现象及它们之间的交互和转换，展示了涌现计算在社会问题研究中的应用潜力。

5 结语

计算能力的持续提高和对于复杂系统中涌现现象研究的不断深入使得我们可以在计算机上使用多主体建模的方式对涌现现象进行仿真和研究，并进一步利用系统的涌现现象来高效求解一些使用传统算法难以解决的问题。作为涌现计算的重要组成部分，群集智能方法已经在多目标优化、数据分类、数据聚类、模式识别、电信QoS 管理、生物系统建模、流程规划、信号处理、机器人控制、决策支持以及仿真和系统辩识等方面得到了广泛的应用。

初期使用较多的符号表征方法是面向任务的，需要理解此任务的人类设计者构建用于表达此任务的特定外部环境，再通过涌现计算的方法得到特定结果。今后涌现计算将越来越多地借鉴神经生物学的研究成果，由面向特定问题的人工符号表征转为面向非特定问题的涌现表征。使用更复杂的更接近于生物神经系统的模型，在内部系统与外部环境的交互中进行自动的涌现表征实现启发式涌现计算是未来的重要发展方向。系统在运行中将在不需要人工重新进行启发式程序的编程或直接对其进行修改的情况下通过增量学习获得针对各种不同任务的技能。在新的更有效的计算范式得到发展的同时，以量子元胞自动机为代表的针对特定涌现计算模式的专用硬件电路也将得到进一步研究，从而为新的计算范式提供专用、更高效和具有更强计算能力的运行支撑平台。作为涌现计算重要通用模型的元胞自动机也正向着更高维度、结构更复杂的方向发展，以提供更强的表达和求解能力。随着计算范式的完善和计算平台的升级，涌现计算的应用也将广泛延伸至自然物理系统、生物系统和社会系统等各个领域，为规律发现和问题求解提供强有力的手段。新的涌现计算研究范式可能带来传统研究方法难以得到的新发现和解决问题的新方法。

对于涌现现象的深入研究将进一步推动涌现计算的发展，同时反过来为我们理解和掌控身边世界的运行提供更有效的工具。

[1]Wolfram S. Universality and complexity in cellular automata [J]. Physica D: Nonlinear Phenomena, 1984, 10(1): 1-35.

[2]Forrest S. Emergent computation: self-organizing, collective, and cooperative phenomena in natural and artificial computing networks: introduction to the proceedings of the ninth annual CNLS conference [J]. Physica D: Nonlinear Phenomena, 1990, 42(1): 1-11.

[3]Holland J H. Emergence: From Chaos to Order [M]. Redwood City: Oxford University Press, 2000.

[4]Kube C R, Bonabeau E. Cooperative transport by ants and robots [J]. Robotics and autonomous systems, 2000, 30(1): 85-101.

[5]Martin M, Chopard B, Albuquerque P. Formation of an ant cemetery: swarm intelligence or statistical accident? [J]. Future Generation Computer Systems, 2002, 18(7): 951-959.

[6]Chung J R, Choe Y. Emergence of memory in reactive agents equipped with environmental markers [J]. Autonomous Mental Development, IEEE Transactions on, 2011, 3(3): 257-271.

[7]Damiani C, Serra R, Villani M, et al. Cell-cell interaction and diversity of emergent behaviours [J]. Systems Biology, IET, 2011, 5(2): 137-144.[8]Tao Z, Xiao R, Wang L. Structure emergence in the evolution of social networks and its case study [J]. Procedia Computer Science, 2013, 17: 981-988.

[9]Seiffertt J, Wunsch D. Intelligence in markets: asset pricing, mechanism design, and natural computation [technology review] [J]. IEEE Computational Intelligence Magazine, 2008, 3(4): 27-30.

[10]Ha S Y, Ha T, Kim J H. Emergent behavior of a Cucker-Smale type particle model with nonlinear velocity couplings [J]. IEEE Transactions on Automatic Control, 2010, 55(7): 1679-1683.

[11]Park J, Kim H J, Ha S Y. Cucker-Smale flocking with inter-particle bonding forces [J]. IEEE Transactions on Automatic Control, 2010,55(11): 2617-2623.

[12]Finke J, Passino K M. Local agent requirements for stable emergent group distributions [J].IEEE Transactions on Automatic Control, 2011, 56(6): 1426-1431.

[13]Niazi M A, Hussain A. Sensing emergence in complex systems [J]. IEEE Sensors Journal, 2011, 11(10): 2479-2480.

[14]Tsilipanos K, Neokosmidis I, Varoutas D. A system of systems framework for the reliability assessment of telecommunications networks [J]. IEEE Systems Journal, 2013, 7(1): 114-124.

[15]Christie P. A fractal analysis of interconnection complexity [J]. Proceedings of the IEEE, 1993, 81(10): 1492-1499.

[16]Hales D, Patarin S. Computational sociology for systems" in the wild": the case of BitTorrent [J]. IEEE Distributed Systems Online, 2005, 6(7): 1-6.

[17]Santini S, Gupta A, Jain R. Emergent semantics through interaction in image databases [J]. IEEE Transactions on Knowledge and Data Engineering, 2001, 13(3): 337-351.

[18]Shimizu M, Ishiguro A, Kawakatsu T. Slimebot: a modular robot that exploits emergent phenomena[C]// Proceedings of the 2005 IEEE International Conference on Robotics & Automation, 2005: 2982-2987.

[19]Lee S I, Cho S B. Emergent behaviors of a fuzzy sensory-motor controller evolved by genetic algorithm [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B Cybernetics, 2001, 31(6): 919-929.

[20]Kahn J M, Katz R H, Pister K S J. Emerging challenges: mobile networking for “smart dust” [J]. Journal of Communications and Networks, 2000, 2(3): 188-196.

[21]Kunniyur S S, Venkatesh S S. Threshold functions, node isolation, and emergent lacunae in sensor networks [J]. IEEE Transactions on Information Theory, 2006, 52(12): 5352-5372.

[22]Olascuaga-Cabrera J G, Lopez-Mellado E, Mendez-Vazquez A, et al. A self-organization algorithm for robust networking of wireless devices [J]. IEEE Sensors Journal, 2011, 11(3): 771-780.

[23]Charles P. Emergent collectives [J]. IEEE Internet Computing, 2011, 15(5): 99-102.

[24]Gravagne I A, Marks R J. Emergent behaviors of protector, refugee, and aggressor swarms [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B Cybernetics, 2007, 37(2): 471-476.

[25]Cucker F, Smale S. Emergent behavior in flocks [J].IEEE Transactions on Automatic Control, 2007, 52(5): 852-862.

[26]Dressler F, Suda T, Carreras I, et al. Guest editorial bio-inspired networking [J].IEEE Journal on Selected Areas in Communications, 2010, 28(4): 521-523.

[27]Liu Y, Passino K M. Stable social foraging swarms in a noisy environment [J]. IEEE Transactions on Automatic Control, 2004, 49(1): 30-44.

[28]Van Drongelen W, Lee H C, Hereld M, et al. Emergent epileptiform activity in neural networks with weak excitatory synapses [J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2005, 13(2): 236-241.

[29]Yu A R, Thompson B B, Marks R J. Competitive evolution of tactical multiswarm dynamics [J]. IEEE Transactions on Systems, Man, and Cybernetics Systems, 2013, 43(3): 563-569.

[30]Ewert W, Marks R J, Thompson B B, et al. Evolutionary inversion of swarm emergence using disjunctive combs control [J]. IEEE Transactions on Systems, Man, and Cybernetics Systems, 2013, 43(5): 1063-1076.

[31]Li N, Marden J R. Designing games for distributed optimization [J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(2): 230-242.

[32]宋玉蓉, 蒋国平.基于一维元胞自动机的复杂网络恶意软件传播研究[J]. 物理学报, 2009, 58(9): 5911-5918. Song Yurong, Jiang Guoping. Research of malware propagation in complex networks based on 1-D cellular automata [J]. Acta Physica Sinica. 2009, 58(9): 5911-5918.

[33]Simons N R S, Bridges G E, Podaima B W, et al. Cellular automata as an environment for simulating electromagnetic phenomena [J]. Microwave and Guided Wave Letters, 1994, 4(7): 247-249.

[34]Mamei M, Roli A, Zambonelli F. Emergence and control of macro-spatial structures in perturbed cellular automata, and implications for pervasive computing systems [J]. Systems, Man and Cybernetics, Part A: Systems and Humans, IEEE Transactions on, 2005, 35(3): 337-348.

[35]Mardiris V A, Karafyllidis I G. Universal cellular automaton cell using quantum cellular automata [J]. Electronics letters, 2009, 45(12): 607-609.

[36]Sapin E, Bull L, Adamatzky A. Genetic approaches to search for computing patterns in cellular automata [J]. Computational Intelligence Magazine, 2009, 4(3): 20-28.

[37]肖人彬, 陶振武. 群集智能研究进展 [J]. 管理科学学报, 2007, 10(3): 80-96. Xiao Renbin, Tao Zhenwu. Development in swarm intelligence [J]. Journal of Management Sciences in China, 2007, 10(3): 80-96.

[38]肖人彬. 面向复杂系统的群集智能 [M]. 北京: 科学出版社, 2013.

[39]Dorigo M, Maniezzo V, Colorni A. The ant system: optimization by a colony of cooperating agents [J]. IEEE Transactions on Systems, Man and Cybernetics-Part B, 1996, 26(1) : 29-41.

[40]Weng J, Luciw M D, Zhang Q. Brain-like emergent temporal processing: emergent open states [J]. IEEE Transactions on Autonomous Mental Development, 2013, 5(2): 89-116.

[41]颜泽贤, 范冬萍, 张华夏. 系统科学导论—复杂性探索 [M]. 北京: 人民出版社, 2006.

[42]金士尧, 黄红兵, 任传俊. 基于复杂性科学基本概念的MAS涌现性量化研究 [J]. 计算机学报, 2009, 32(1): 17-29. Jin Shiyao,Huang Hongbing,Ren Chuanjun. Emergence oriented research on MAS with quantifications based on the notions in science of complexity [J]. Chinese Journal of Computers, 2009, 32(1): 17-29.

[43]尼科利斯 G, 普里戈金 I. 非平衡系统中的自组织 [M]. 徐锡申,译. 北京: 科学出版社, 1986

[44]哈肯 H. 协同学导论 [M]. 张纪岳,郭治安,译. 西安: 西北大学科研处, 1981.

[45]Liu J, Jin X, Tsui K C. Autonomy-oriented computing (AOC): formulating computational systems with autonomous components [J]. IEEE Transactions on Systems, Man and Cybernetics, Part A Systems and Humans, 2005, 35(6): 879-902.

[46]李健, 李刚, 孙林岩. 分散化供应链的自组织演化机制建模与仿真 [J]. 数学的实践与认识, 2008, 38(6): 26-34. Li Jian, Li Gang, Sun Linyan. Modeling and simulation of distributed supply-chain self-organizing evolution mechanism [J]. Mathematics in Practice and Theory, 2008, 38(6): 26-34.

[47]顾珊珊, 陈禹. 复杂适应性系统的仿真与研究——基于CAS理论的交通模拟 [J]. 复杂系统与复杂性科学, 2004, 1(1): 82-88. Gu Shanshan, Chen Yu. Modeling & simulation of complex adaptive system-a traffic simulation system [J]. Complex Systems and Complexity Science, 2004, 1(1): 82-88.

[48]张嗣瀛. 复杂性科学, 整体规律与定性研究 [J]. 复杂系统与复杂性科学, 2005, 2(1): 71-83. Zhang Siying. Complexity science, rules of the whole systems and the qualitative researches [J]. Complex Systems and Complexity Science, 2005, 2(1): 71-83.

[49]罗吉贵, 刘曾荣. 从同步到涌现 [J]. 复杂系统与复杂性科学, 2005, 2(1): 29-32. Luo Jigui, Liu Zengrong. From synchronization to emergence [J]. Complex Systems and Complexity Science, 2005, 2(1): 29-32.

[50]Winfree A T. Biological rhythms and the behavior of populations of coupled oscillators [J]. Journal of Theoretical Biology, 1967, 16(1):15-42.

[51]Araki H. International symposium on mathematical problems in theoretical physics [J]. Lecture Notes in Physics, 1975, 39.

[52]Néda Z, Ravasz E, Brechet Y, et al. Self-organizing processes: The sound of many hands clapping [J]. Nature, 2000, 403(6772): 849-850.

[53]Strogatz S H. Fromkuramoto to crawford: exploring the onset of synchronization in populations of coupled oscillators [J]. Physica D: Nonlinear Phenomena, 2000, 143(1): 1-20.

[54]李德毅, 刘坤, 孙岩, 等. 涌现计算: 从无序掌声到有序掌声的虚拟现实 [J]. 中国科学 E辑: 信息科学, 2007, 37(10): 1248-1257. Li Deyi, Liu Kun, Sun Yan, et al. Emergent computation: the virtual reality of applause from disorder to ordered [J]. Science in China(Series E: Information Sciences), 2007, 37(10): 1248-1257.

[55]Li D, Liu K, Sun Y, et al. Emerging clapping synchronization from a complex multiagent network with local information via local control [J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2009, 56(6): 504-508.

[56]Wang D L. Emergent synchrony in locally coupled neural oscillators [J]. IEEE Transactions on Neural Networks, 1995, 6(4): 941-948.

[57]Zhang Q, Lu J, Lu J, et al. Adaptive feedback synchronization of a general complex dynamical network with delayed nodes [J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2008, 55(2): 183-187.

[58]Chen M. Chaos synchronization in complex networks [J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2008, 55(5): 1335-1346.

[59]Boulden S, Iorio A W, Abbass H A. Learning synchronization in networked complex systems using genetic algorithms[C]// IEEE Congress on Evolutionary Computation, 2010: 1-8.

[60]汪镭, 周国兴. 用Hopfield神经网络进行交流传动系统参数辨识 [J]. 模式识别与人工智能， 1996, 9(3): 291-296. Wang Lei, Zhou Guoxing. Hopfield neural network based AC drive system parameters identification [J]. Pattern Recognitien and Artificial Intelligence, 1996, 9(3): 291-296.

[61]康琦, 安静, 汪镭, 等. 自然计算的研究综述 [J]. 电子学报, 2012, 40(3): 548-558. Kang Qi, An Jing, Wang Lei, et al. nature-inspired computation: a survey [J]. Aacta Electronica Sinica, 2012, 40(3): 548-558.

[62]汪镭, 康琦, 吴启迪. 自然计算——人工智能的有效实施模式 [J]. 系统工程理论与实践, 2007, 5: 126-134. Wang Lei, Kang Qi, Wu Qidi. Nature-inspired computation-effective realization of artificial intelligence [J]. Systems Engineering-Theory & Practice, 2007, 5: 126-134.

[63]Dong J, Zhang Z, Ma D. Emergent phenomenon and the local information based DTA model [C]// IEEE Intelligent Transportation Systems, 2003, 2: 1273-1277.

[64]Sotelo M A, Van Lint J W C, Nunes U, et al. Introduction to the special issue on emergent cooperative technologies in intelligent transportation systems [J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(1): 1-5.

[65]Linkens D A, Nyongesa H O. Learning systems in intelligent control: an appraisal of fuzzy, neural and genetic algorithm control applications [J]. IEEE Proceedings Control Theory and Applications, 1996, 143(4): 367-386.

[66]Maturana F P, Staron R J, Hall K H. Methodologies and tools for intelligent agents in distributed control [J]. IEEE Intelligent Systems, 2005, 20(1): 42-49.

[67]Arena P, Fortuna L, Frasca M, et al. A CNN-based chip for robot locomotion control [J]. IEEE Transactions on Circuits and Systems I: Re-gular Papers, 2005, 52(9): 1862-1871.

[68]Krasny D P, Orin D E. Generating high-speed dynamic running gaits in a quadruped robot using an evolutionary search [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2004, 34(4): 1685-1696.

[69]Arena P, Patanè L. Simple sensors provide inputs for cognitive robots [J]. IEEE Instrumentation & Measurement Magazine, 2009, 12(3): 13-20.

[70]Floreano D, Mondada F. Evolution of homing navigation in a real mobile robot [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 1996, 26(3): 396-407.

[71]Li Y, Tang Z, Xia G P, et al. A positively self-feedbacked Hopfield neural network architecture for crossbar switching [J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2005, 52(1): 200-206.

[72]Dogaru R. Applications of Emergent Computation in Reaction-Diffusion CNNs for Image Processing[C]// 19th IEEE International Conference on Control Systems and Computer Science, 2013: 370-377.

[73]杨淑莹, 刘旭鹏, 陶冲, 等. 基于免疫猫群优化算法的矢量量化的码书设计及语音识别 [J]. 模式识别与人工智能, 27(7): 577-583. Yang Shuying, Liu Xupeng, Tao Chong, et al. Vector quantization codebook design and speech recognition based on immune cat swarm optimization algorithm [J]. Pattern Recognition and Artificial Intelligence, 27(7): 577-583.

[74]Ha S Y, Ha T, Kim J H. Emergent behavior of a Cucker-Smale type particle model with nonlinear velocity couplings [J]. IEEE Transactions on Automatic Control, 2010, 55(7): 1679-1683.

[75]Kahrobaee S, Rajabzadeh R A, Soh L K, et al. A multiagent modeling and investigation of smart homes with power generation, storage, and trading features [J]. IEEE Transactions on Smart Grid, 2013, 4(2): 659-668.

[76]Tero A, Takagi S, Saigusa T, et al. Rules for biologically inspired adaptive network design [J]. Science, 2010, 327(5964): 439-442.

[77]Seiffertt J, Wunsch D. Intelligence in markets: asset pricing, mechanism design, and natural computation technology review [J]. IEEE Computational Intelligence Magazine, 2008, 3(4): 27-30.

[78]Chung J R, Choe Y. Emergence of memory in reactive agents equipped with environmental markers [J]. IEEE Transactions on Autonomous Mental Development, 2011, 3(3): 257-271.

[79]Lee S M, Pritchett A R. Predicting interactions between agents in agent-based modeling and simulation of sociotechnical systems [J]. IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, 2008, 38(6): 1210-1220.

[80]Hurlburt G, Voas J, Miller K, et al. A nonlinear perspective on higher education [J]. Computer, 2010 (12): 90-92.

[81]Kong Z, Mettler B. Modeling human guidance behavior based on patterns in agent-environment interactions [J]. IEEE Transactions on Human-Machine Systems, 2013, 43(4): 371-384.

[82]Sanchez-Cortes D, Aran O, Mast M S, et al. A nonverbal behavior approach to identify emergent leaders in small groups [J]. IEEE Transactions on Multimedia, 2012, 14(3): 816-832.

[83]Izumi K, Ueda K. Phase transition in a foreign exchange market-analysis based on an artificial market approach [J]. IEEE Transactions on Evolutionary Computation, 2001, 5(5): 456-470.

[84]栾笑天, 吴桐水, 寇勇刚. 基于CA方法的航空物流市场演化模型设计 [J]. 复杂系统与复杂性科学, 2013, 10(4): 31-40. Luan Xiaotian, Wu Tongshui, Kou Yonggang. Designing the evolution model of aviation logistics market with cellular automata [J]. Complex Systems and Complexity Science, 2013, 10(4): 31-40.

[85]Koritarov V S. Real-world market representation with agents [J]. IEEE Power and Energy Magazine, 2004, 2(4): 39-46.

[86]Chicco G, Napoli R, Piglione F, et al. Emergent electricity customer classification [J]. IEE Proceedings-Generation, Transmission and Distribution, 2005, 152(2): 164-172.

[87]龚小庆, 范文涛, 丁义明. 建立系统科学基础理论框架的一种可能途径与若干具体思路( 之八) —— 固定环境中的稳态涌现 [J]. 系统工程理论与实践, 2003, 8: 1-7. Gong Xiaoqing, Fan Wentao, Ding Yiming. A possible approach to the framework of the fundamental theory of system science: part eight [J]. Systems Engineering-theory & Practice, 2003, 8: 1-7.

[88]龚小庆, 王展. 关于Zipf律的一点注记 [J]. 复杂系统与复杂性科学, 2008, 5(3): 73-78. Gong Xiaoqing, Wang Zhan. A note on the zipf′s law [J]. Complex Systems and Complexity Science, 2008, 5(3): 73-78.

[89]龚小庆. 经济系统涌现和演化——复杂性科学的观点 [J]. 财经论丛, 2004, 5(111): 12-18. Gong Xiaoqing. Researches on emergence and evolution of economy——in the view of complexity sciences [J]. Collected Essays on Finance and Economics, 2004, 5(111): 12-18.

[90]赵剑冬, 黄战. 基于Agent的经济社会系统建模与仿真研究 [J]. 复杂系统与复杂性科学, 2011, 8(4): 59-67. Zhao Jiandong, Huang Zhan. A study on agent based social-economic system modeling and simulation [J]. Complex Systems and Complexity Science, 2011, 8(4): 59-67.

[91]Zeng F, Decraene J, Low M Y H, et al. Evolving optimal and diversified military operational plans for computational red Teaming [J]. IEEE Systems Journal, 2012, 6(3): 499-509.

[92]Lewis R, Paechter B. Finding feasible timetables using group-based operators [J]. IEEE Transactions on Evolutionary Computation, 2007, 11(3): 397-413.

[93]王飞跃, 史帝夫·兰森. 从人工生命到人工社会—复杂社会系统研究的现状和展望 [J]. 复杂系统与复杂性科学, 2004, 1(1): 33-41. Wang Feiyue, Lansing J S. From artificial life to artificial societies—new methods for studies of complex social systems [J]. Complex Systems and Complexity Science, 2004, 1(1): 33-41.

(责任编辑 耿金花)

Emergent Computation: an Overview

LI Jin，XIAO Renbin

(School of Automation, Huazhong University of Science and Technology, Wuhan 430074, China)

Firstly we introduce emergent phenomenon in complex systems and the basic principle of emergent computation. Secondly an important emergent computation model — cellular automata (CA) is demonstrated, and the relationship between emergent computation and swarm intelligence is illustrated. Then we discuss some key themes such as the mapping from source problems to emergent computation models, self-organization and synchronization. At last we review the application of emergent computation in aspects of engineering computation and social computation.

emergent computation；swarm intelligence；cellular automata

1672-3813(2015)04-0001-13;

10.13306/j.1672-3813.2015.04.001

2014-02-25 ；

2014-10-23

教育部高等学校博士学科点专项科研基金(20130142110051)

李劲(1980-)，男，河北雄县人，博士，主要研究方向为涌现计算，群集智能。

肖人彬(1965-)，男，湖北武汉人，博士，教授，主要研究方向为复杂系统，复杂社会管理。

TP18

A