具有圈性结构的城市交通网络承载能力分析

杨国菁，吴建军

(北京交通大学轨道交通控制与安全国家重点实验室，北京 100044)

具有圈性结构的城市交通网络承载能力分析

杨国菁，吴建军

(北京交通大学轨道交通控制与安全国家重点实验室，北京 100044)

建立了圈性网络的演化机理，研究了相同路网规模下具有不同圈性网络拓扑结构的交通承载能力，发现在流量不断加载并最终达到饱和状态的过程中，当圈性较小或者较大时，网络流量都比较容易达到饱和状态。相反，当圈性在0.54附近时，网络则更不容易达到拥堵状态。

城市交通；承载力；网络结构；圈性

0 引言

随着城市化进程的加速，目前城市特别是大城市的交通承载能力已经逼近甚至超过了当前的极限,从而导致城市交通问题愈演愈烈。但是，城市的发展不可能突破土地资源的限制，交通的发展也不可能严重超过系统的承载能力。各城市积极地通过各种方式来缓解交通问题并尽可能提高城市的交通承载能力。研究具有怎样的拓扑结构才可以使承载的交通流量达到最大不仅是合理规划城市道路网络，缓解城市交通拥堵的关键，也是研究城市交通网络演化的基础。

随着人们对承载力概念认识的不断加深，国内外学者从不同角度对城市交通承载力的大小进行了估算。从优化角度看，Ford 和 Fulkerson[1]应用图论中最大流最小割集定理的方法建立了路网容量模型。Asakura[2]第一个针对平衡网络交通容量问题提出求解平衡网络交通容量问题的双层规划模型和相应的启发式算法。Yang等[3]在总结先前研究成果的基础上提出城市交通承载力问题是一个系统问题，并改进了求解城市交通承载力的双层规划模型。在此基础上，侯德勋[4]建立了评价交通承载力大小的体系，提出了求解城市交通设施承载力的多目标双层规划模型并用遗传算法求解。詹歆晔等[5]基于“机动车在驶量”构建了由路网资源、燃油供给和大气环境3个模块组成的交通承载力宏观定量模型。李荣等[6]在分析交通承载力的关键影响因素的基础上，建立交通承载力定量计算模型，通过关键因素的时间序列分析对交通承载力进行预测。Li等[7]从宏观层面重新定义了城市交通承载力，结合高峰小时交通量和拥堵指数给出了交通承载力的计算方法。基于多因素分析法研究了影响北京市交通承载力的关键因素，应用因子分析和非线性回归方法得到城市交通承载力与这些影响因素之间的内在关系。王乾等[8]从系统工程角度通过对交通环境承载力、环境容量进行研究，提出了基于灰色模型的交通承载力确定方法并进行了应用。随着网络复杂性研究的兴起，许多学者开始尝试研究道路网络结构与交通承载力之间的关系。吴建军[9]结合用户均衡配流与复杂网络理论，研究了网络拓扑结构对交通堵塞的影响以及网络拓扑与交通承载流量之间的关系，并进一步讨论了最优的交通网络拓扑。贾顺平等[10]研究了居民出行特性与路网承载力下的城市交通状态。许明涛[11]建立了在容量限制的情况下城市道路和交通的互演化模型。Zhao等[12]提出了一种考虑道路投资及其路段能力的城市道路交通网络演化模型。龙雪琴等[13]通过简化公路网系统，建立了公路网结构自组织演化框架，对演化过程进行了仿真研究。

综上可知，对于城市交通承载力的概念和定量计算已有较成熟的研究，但是以往的研究是基于城市可以不断扩张的模式，还缺乏对给定路网规模的条件下如何优化交通网络结构的研究。一般情况下，由于城市交通网络结构具有小世界特性，因此可以用圈性和树性来度量。圈性代表了路网成环成网的程度，即网络连通性的大小，圈性越大连通性越好。而树性则表示路网呈现树状结构的程度。树性大的网络，网络结构相对简单，道路的建设成本相对较少。圈性和树性是一对相对的概念，圈性越大的网络其树性越小，反之亦然。随着城市规模的不断扩张，城市道路长度也在不断增加，城市道路网却显得越来越拥堵，如何在有限的资源约束下，更加合理地规划城市的道路网络，找出道路长度一定情况下，承载力最大时网络的圈性大小显得尤为重要。在保证网络连通的前提下，通过对节点数相同的全连通网络随机删除网络中的边，最终得到边数相同，圈性不同的连通网络。从而建立具有不同圈性特性的路网结构演化模型，并对得到的网络进行UE平衡配流，研究了不同网络上的流量分布特性，通过对不同网络结构不断加载相同单位流量，探讨了网络结构与城市交通承载力之间的相关关系。研究发现，在逐步向网络加载流量的过程中，圈性较大的网络和圈性较小的网络均比较快达到拥堵状态，而圈性在0.5左右时，网络的承载能力反而更大。由此可知，网络的承载力随着圈性的逐渐增大呈现出先增大后减小的趋势。从而找到承载力最大的网络结构，通过研究路网演化过程中交通承载力的变化，探讨了城市交通承载力与路网结构之间的协同演化关系，揭示了随着路网结构的变化，承载力的变化规律。为合理规划道路结构，缓解交通拥堵提供一定的依据。

1 网络产生机制

1.1 交通道路网络结构特征参量

为了研究道路网络成环成网的特性对网络承载流量的影响，引入Haggett等[14]在1969年提出的圈和树的概念。即对于一个连通的网络来说，如果从网络上某一点出发经过若干条边(大于等于3)之后还能回到起点，则称经过的这些边围成了一个圈，称在圈上的边为圈边。如果一条边只在一个圈上则认为这条边属于一个环，如果一条边属于多个圈就表明这条边在网上，如果一个边不在任何圈上则认为这条边在树上，称这条边为树边。用圈性(φcircuit)表示城市道路网络成环成网的程度，树性(φtree)表示城市道路网络成树状程度。不考虑每条边的长短差异和每条道路的等级差异，给出路网圈性及树性的计算公式

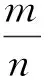
(1)

φcircuit=1-φtree

(2)

其中，m为网络中属于树的边的个数，n为网络中边的个数。

本文通过邻接矩阵表示两个点之间是否有边相连，相连的为1，不相连的为0，因为道路网络为无向图，所以邻接矩阵为主对角元素为0的对称矩阵A。则网络中边的个数m为网络中所有非零元素和的一半。假设lij为网络中i点到j点的一条边(即Aij=1)，若去掉该边之后网络不连通了，则说明该条边为树边，否则为圈边。

1.2 圈性网络产生机制

节点为q的全连通的网络通过逐渐删除网络中的边，得到给定边数为N，不同圈性的网络结构的生成过程为：

步骤1：生成一个全连通网络(即生成一个对角线元素为0其他元素均为1的邻接矩阵A)；

步骤2：随机删除一条边(即在邻接矩阵中随机找到一个非零元素Aij，令Aij=0,Aji=0)判断删除边后网络连通性，若不连通则将删除的边恢复(即令Aij=1,Aji=1)重复执行步骤2。若网络连通，则执行步骤3；

步骤3：计算网络的圈性φ0，判断是否满足φ0>φn(φn为终止条件)，若不满足，则将删除的边恢复(Aij=1,Aij=1)。计算网络中剩余边的个数；

步骤4：重复步骤2，计算网络的圈性，判断是否满足φk>φn，若不满足，则将删除的边恢复(Aij=1,Aji=1)；

步骤5：重复步骤2，3，4。当剩余的边数n=N时停止循环。得到需要的网络;

步骤6：为了便于比较不同φn值对城市交通网络承载力的影响，对于给定的不同φn值，重复以上步骤2至5，便可以得到满足给定圈性值的网络。

2 流量加载

2.1 用户平衡配流

1952年，Wardrop[15]提出平衡配流原则：在起讫点之间所有可供选择的路径中，所有被使用者利用的各条路径上的出行费用全都相等，而且不大于未被利用路径上的出行费用。又可称为用户平衡配流(User Equilibrium，简称UE)。满足这一原则的交通状态被定义为Wardrop平衡状态，Beckmann采用以下数学形式描述Wardrop平衡状态：

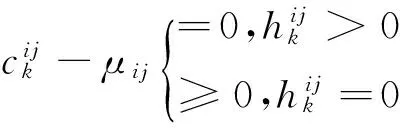
(3)

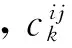
通常情况下，UE平衡配流问题被认为是一个凸规划问题，1956年Beckmann等[16]提出了一种满足Wardrop原则的数学规划模型:

(4)

(5)

(6)

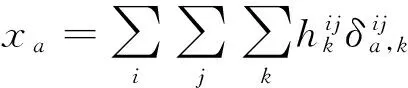
(7)

(8)

其中，xa为路段a上的交通量，ta为路段a上流量为xa时的阻抗，I为产生交通量的起始节点的集合，J为交通量的终讫节点的集合，i为一个起始节点，∀i∈I,j为一个终讫节点，∀j∈J，qij为O-D对i-j的交通需求量。

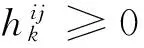
该模型中的目标函数是所有路段阻抗函数积分的和，方程(5)代表路径流量与O-D流量之间的守恒关系，方程(6)保证了所有路径的流量都是非负的，方程(7)是路段流量与路径流量之间的关联关系，有：

(9)

需要注意的是，该用户均衡配流模型必须满足以下两个假设：1)路段的阻抗仅仅是该路段流量的函数，与其他路段上的流量没有联系；2)假设路段阻抗是流量的严格增函数。用数学形式表示为

(10)

随机给定各个路段的零流阻抗t0，任意两点之间的O-D交通量都是相同的，即O-D需求矩阵是对角线为0其余元素均为1的对称矩阵。按照用户均衡理论对演化得到的网络分别进行流量加载，则流量为xa时路段的阻抗函数按照美国公路局提供的(U.S.BureauofPublicRoads—BPR)公式计算。

(11)

其中，xa为路段a上的交通量，ua为路段a的最大承载流量，ta为路段a上流量为xa时的阻抗，α，β为固定参数，模型中取α为0.15，β为4。

2.2 算法

对于该模型的求解一般用Frank-Wolfe方法，该算法是Frank和Wolfe[17]于1956年求解线性约束问题时提出的，通常简称F-W算法。算法的基本思想是，在每次迭代中，将目标函数线性化，通过解线性规划来求得下降可行方向，进而沿此方向在可行域内作一维搜索以得到新的迭代点。

迭代次数为n时，目标函数值Z(x)下降的搜索方向应由求解下面的线性规划问题得到：

minZn(y)=

(12)

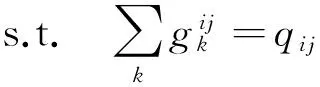
(13)

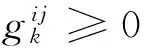
(14)

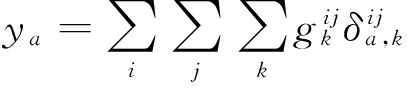
(15)

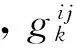
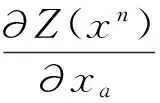
(16)

该模型实际上是在各路段阻抗固定为ta的条件下使网络总阻抗最小的经典运输问题。F-W算法的具体求解过程可参见参考文献[18]。

2.3 拥堵度

对于既有的路段，如果路段上的流量超过了其最大的承载流量则认为该路段处于拥堵状态。在本模型中，假设一共有N条路段，给定路段a(a∈N)最大承载流量为ua，零流阻抗为t0。假设通过用户平衡配流最终达到平衡状态的过程中，每一步迭代，所有O-D对之间均产生一个单位的交通流量。因此可以确定平衡状态下每条路段上的交通流量。如果某条路段上的交通流量超过其最大承载流量，则说明该路段属于拥堵路段，且记拥堵路段数目T加1。计算公式为

(17)

观察不同拓扑结构网络的拥堵路段的变化情况，进而分析出不同网络结构中最优的拓扑结构。道路交通状态用道路交通拥堵程度表示，即实际发生的交通拥堵路段与城市道路总路段的比值．按照计算公式(18)：

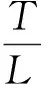
(18)

其中，e为网络的拥堵程度，T为网络中拥堵路段的个数，L为网络中总的路段的个数。

3 算例分析

3.1 网络的生成及流量分配

以节点数为50的网络为例，在节点全连通的情况下，按照前面分析的方法，得到边数为56，圈性为0.33,0.43,0.54,0.66,0.75,0.86,0.96的网络的邻接矩阵，在考虑网络拓扑特性的基础上研究分析了不同圈性情况下，对网络中的道路随机分配道路的容量，按照UE平衡原理，对不同网络逐次加载相同流量。分析不同圈性情况下，网络承载流量变化情况。计算随着不断给网络加载流量，不同网络结构下路段拥堵情况的变化，最终找出相同流量下，网络的拥堵度最小时网络的圈性大小，即得到比较适合的圈性大小的网络结构。

3.2 结果分析

分别对不同圈性的网络进行流量加载250步，可以得到不同圈性的网络承载相同流量的拥堵程度变化如图1所示。从图1中可以看出随着流量的增加，即在网络的交通流从自由流向拥堵流演化的过程中，拥堵路段的增加量是逐渐减少的。

分别取流量加载次数初始阶段(如图2a)和流量趋于饱和阶段(如图2b)的网络拥堵状况进行分析。从图2a和图2b对比可以看出，不同网络之间的拥堵度差异随着流量的加载有不断扩大的趋势。这就说明在交通流量较小的情况下网络的圈性大小对交通拥堵程度的影响并不明显，但是随着网络中交通量的大幅增加，网络拓扑结构的影响也逐渐明显。从图2b中可以明显看出圈性为0.54的网络在同等迭代次数条件下拥堵程度是最少的，而圈性为0.33和0.96的网络拥堵程度是较高的。也就是说在城市道路自由演化的过程中圈性为0.54左右的道路网络在相同条件下能承载更多的流量，更能适应由于城市的不断发展而不断增加的交通流量的需求，相同情况下，该网络结构的交通压力更小。

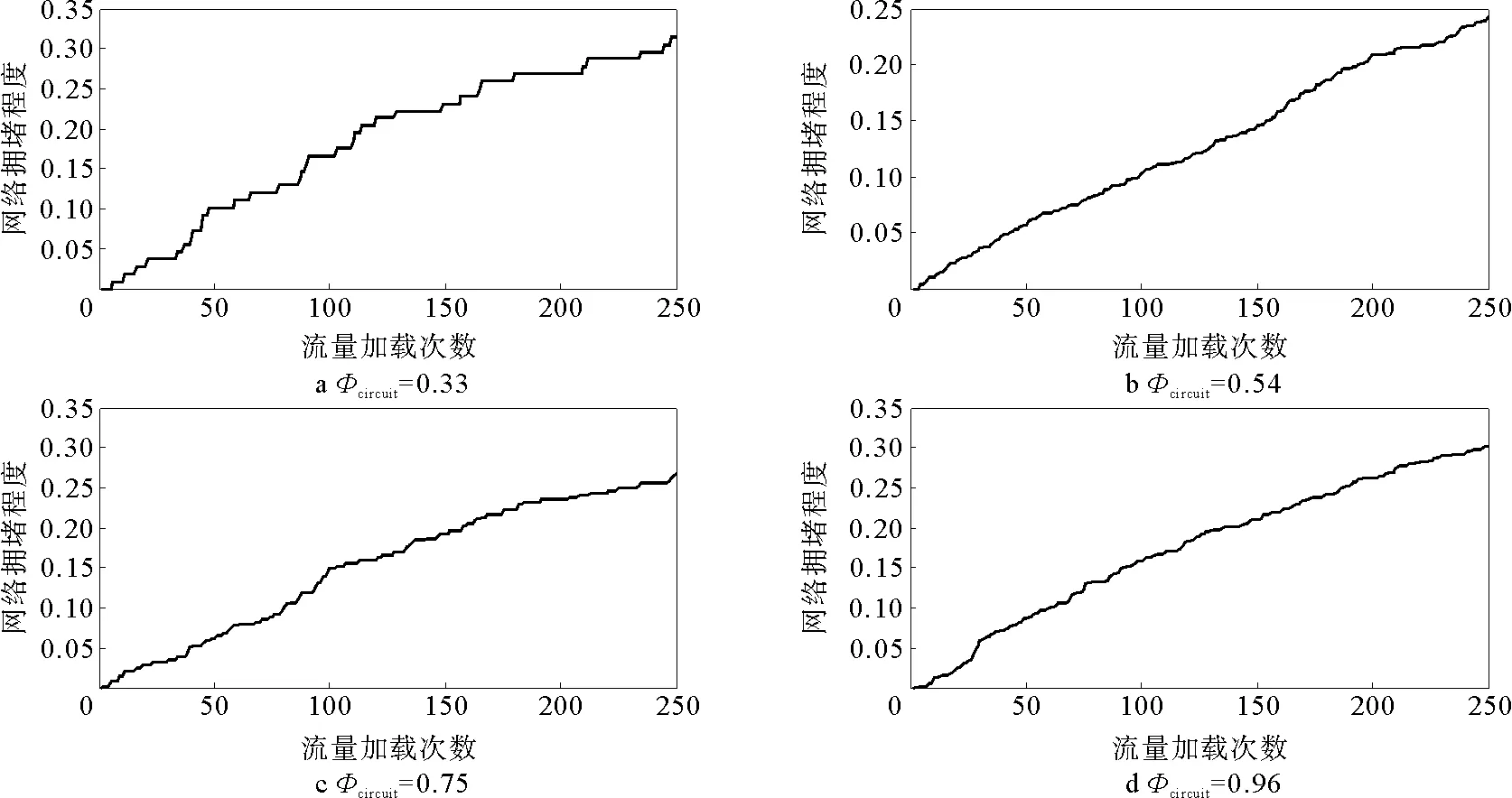
图1 不同圈性网络拥堵度随流量增加的变化

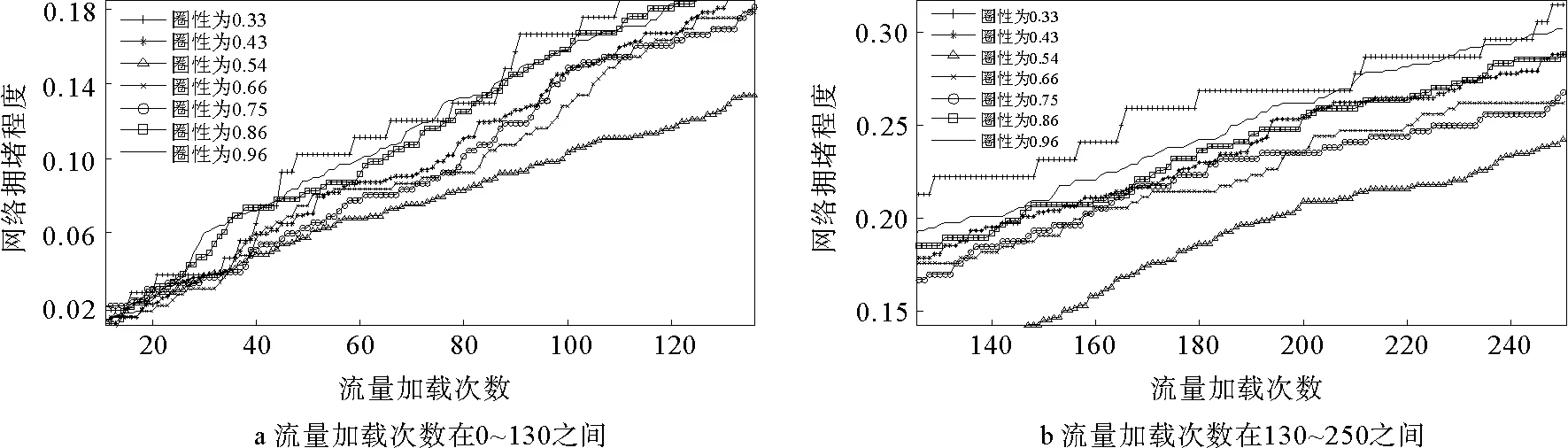
图2 不同圈性网络的拥堵情况

分别对迭代100步，150步，200步和250步的不同圈性下的拥堵程度做进一步分析，如图3所示。从图3可以看出，随着迭代次数的增加,不同圈性网络在承载相同流量情况下的拥堵路段的增加量的变化逐渐趋于平和，这与随着迭代次数的增加，流量逐渐趋于饱和是有关系的。说明不同圈性情况下随着迭代次数的不断增加，网络最终的演化方向都是趋于全部拥堵。从图3中可以清楚地看出在迭代次数相同的情况下，随着圈性的不断增大，网络拥堵情况的变化趋势是先减少后增大的。也就是说，圈性为0.5左右的时候是拥堵情况较小的网络结构。

以北京地铁网络为例，将各个地铁站看成一个节点，两个站点之间的线路看成一条无向的边，换乘站不同线路近似看成相交于同一个点，不考虑换乘站的换乘距离和换乘时间，则可以把地铁网络看成一个无向图。按照前面所说的理论，统计出地铁网络中属于环上的边有156条，属于边上的边有105条，按照前面所给公式可以计算出北京地铁的圈性为0.597 7，与结果分析中一致，是承载力较大的网络结构。

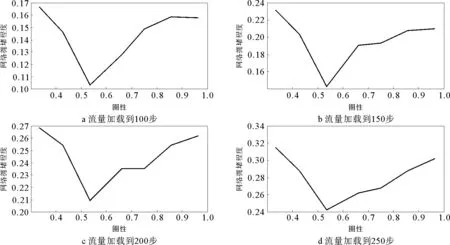
图3 相同迭代次数不同圈性的拥堵情况

4 总结与展望

近些年复杂网络的快速发展为缓解交通拥堵问题提供了一个全新的思路，它从拓扑结构上说明了什么样的网络拓扑结构是有利于城市交通的发展的。随着计算机技术的不断发展和复杂网络的深入研究，通过对网络的模拟仿真即可分析得到网络的拓扑特性，为解决交通拥堵问题提供新的途径。本文主要结合了网络拓扑结构和UE均衡配流，运用计算机模拟，研究了不同圈性网络条件下路网的承载能力变化，而造成城市交通拥堵的因素有很多，除了经济的发展与交通基础设施建设的不协调、城市交通管理混乱，既有交通缺乏整合之外，最重要的是车辆增加过快和路网结构不合理。单纯依靠修建一条道路来缓解交通拥挤问题不仅需要投入大量的资本，还有可能产生更大的拥堵出现Braess诡异现象，使得交通拥堵问题更加严峻。因此，寻找最大承载力的路网拓扑结构有着非常重要的现实意义。尤其是对新城区的建设，不仅可以使得新城区快速发展又可以避免其日后陷入拥堵的状况，还能减少开支，避免资源的浪费。

本文仅是从网络的树性和圈性这一方面来分析了拓扑结构对网络承载力的影响，对于理解网络的拓扑结构和弄清网络的性能有很大帮助。今后将环型、放射型、网状、蜂窝状等网络拓扑结构与复杂网络中的规则网络、随机网络、小世界网络、无标度网络相结合进行定量研究，探索出承载力最大的网络拓扑结构。

[1]Ford L R Jr, Fulkerson D R. Solving the transportation problem [J].Management Science.1956， (10): 24-32.

[2]Asakura Y. Maximum capacity of road network constrained by user equilibrium conditions [C]//The Proceeding of 24th Annual Conference of the UTSG，Newcastle，1992:4.

[3]Yang H, Bell G H，Meng Q. Modeling the capacity and level of service of urban transportation network[J]. Transportation Research Part B,2000,34(4):255-275.

[4]侯德勋． 城市交通承载力研究[D].上海: 同济大学, 2008． Hou De Xun. The study of traffic carrying capacity[D]. Shanghai： Tongji University, 2008.

[5]詹歆晔，郁亚娟，郭怀成，等.特大城市交通承载力定量模型的建立与应用[J].环境科学学报，2008，28(9)：1923-1931 Zhan Xinye, Yu Yajuan, Guo Huaicheng, et al. Modeling and application of metropolitan transportation support capacity[J].Acta Scientiae Circumstantiae, 2008,28(9): 1923-1931.

[6]李荣，吴建军.北京市交通承载力预测研究[J].山东科学，2013,26(2):98-111. Li Rong, Wu Jianjun.Prediction of Beijing traffic carrying capacity[J]. Shandong Science.2013.26(2):98-111.

[7]Li Tongfei, Wu Jianjun. Carrying capacity of urban traffic network: modeling and empirical analysis[C] //2013 International Conference on Industrial Engineering and Management Science. Shanghai:DEStech，2013, 566-572.

[8]王乾，雷黎．基于灰色预测模型的交通环境承载力研究[J].科学之友,2008,7(20) :70-72． Wang Qian, Lei Li. Study on traffic capacity based on grey forecasting model [J].Friend of Science Amateurs,2008,7(20):70-72.

[9]吴建军.城市交通网络拓扑结构复杂性研究[D].北京：北京交通大学，2008. Wu Jianjun. The study of Urban traffic network topology complexity[D]. Beijing： Beijing Jiaotong University, 2008.

[10]贾顺平，彭宏勤，刘爽． 基于居民出行特性与路网承载力的城市交通状态研究[J]． 交通运输系统工程与信息，2011,11(5) : 81-85． Jia Shunping, Peng Hongqin, Liu Shuang. Urban traffic state estimation considering resident travel characteristics and road network capacity[J].Journal of Transportation Systems Engineering and Information Technology, 2011,11(5):81-85.

[11]许明涛，吴建军． 基于容量限制的道路与城市交通的互演化研究[J].山东科学，2012， 25( 4) :58-63． Xu Mingtao, Wu Jianjun. Research on limited capacity based co-evolution of road surface and urban traffic[J]. Shandong Science, 2012,25(4):58-63．

[12]Zhao F X, Sun H J, Wu J J, et al. Urban road network evolution to maximize the capacity[J]. Procedia-Social and Behavioral Sciences, 2014, 138: 251-258.

[13]龙雪琴, 王建军, 关宏志. 基于建设成本约束的公路网结构演化研究[J]. 交通运输系统工程与信息, 2014, 14(4): 23-29. Long Xueqin, Wang Jianjun, Guan Hongzhi. Self-organization of roads network structure based on restraint of construct cost[J]. Journal of Transportation Systems Engineering and Information Technology,2014, 14(4): 23-29.

[14]Haggett P, Chorley R J. Network Analysis in Geography[M]. London: Edward Arnold, 1969.

[15]Wardrop J G. Some theoretical aspects of road traffic research[C]//ICE Proceedings Engineering Divisions. London:Thomas Telford, 1952, 1(3): 325-378.

[16]Beckmann M J, McGuire C B, Winsten C B. Studies in the economics of transportation[M]. New Haven:Yale University Press, 1956.

[17]Frank M, Wolfe P. An algorithm for quadratic programming[J].Naval Research Logistics Quarterly,1956,3:95-110.

[18]黄海军. 城市交通网络平衡分析: 理论与实践[M]. 北京:人民交通出版社, 1994.

(责任编辑 耿金花)

Carrying Capacity Analysis of the Urban Traffic Network Under Different Circuitness

YANG Guojing,WU Jianjun

(State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044,China)

In this paper, we establish the evolution mechanism of the circuitness of the urban traffic network, and obtain the different topologies of networks. Then, we study the traffic carrying capacity under different network topology structure. As a result, with the increasing network traffic flow, it is much easier to be saturated for the smaller and larger cirucitness. On the contrary, the network has the largest carrying capacity when the circuitness is about 0.54.

urban traffic; network carrying capacity; network structure; circuitness

1672-3813(2015)04-0036-07;

10.13306/j.1672-3813.2015.04.005

2014-08-01 ；

2014-11-06

国家自然科学基金(71271024)；教育部新世纪优秀人才支持计划(NCET-12-0764)

杨国菁(1989-)，女，河南新乡人，硕士研究生，主要研究方向为交通运输系统分析与集成。

U491.1

A