基于局部保持的KNN算法

(西华大学计算机与软件工程学院，四川 成都 610039)

·计算机软件理论、技术与应用·

基于局部保持的KNN算法

曾俊杰，王晓明*，杨晓欢

(西华大学计算机与软件工程学院，四川 成都 610039)

距离度量对K近邻(KNN)算法分类精度起着重要的作用。传统KNN算法通常采用欧氏距离，但该距离将所有特征的差别平等对待，忽略了数据的局部内在几何结构特征。针对此问题，文章借鉴局部保持投影(LPP)的基本思想，在考虑数据的局部内在几何结构特征基础上，依据类内局部保持散度矩阵构造一种距离度量新方法，利用该距离度量提出一种局部保持K近邻算法。实验结果表明，与采用欧氏距离和传统马氏距离的KNN相比，本算法能够得到更好的分类精度。

K-近邻;局部保持投影;马氏距离

分类不仅在模式识别、机器学习、数据挖掘和人工智能等相关领域有广泛的研究，而且在医疗诊断、信用评估、选择购物等生活实践中也得到了广泛的应用。K近邻(K-nearest neighbor，KNN)算法[1-2]具有直观、简单、有效、易实现等特点，成为分类算法中比较常用的算法之一。该算法由Cover和Hart在1967年提出，是一种基于向量空间模型的算法，通过计算向量之间的相似度来确定待分类对象的类别。与其他分类算法不同，KNN算法不用提前设计出分类器。同时，该方法对较复杂的问题也有很好的分类能力。

KNN中距离度量[3-4]的设计会直接影响该分类算法的性能。传统的KNN算法采用欧氏距离[5]，这种距离度量本质上会赋予每个属性相等的权值，这样近邻间的距离会被大量的不相关属性所支配，分类效果就会受到很大的影响。为了克服这个缺点，卢伟胜等[6]构造了加权的欧氏距离，它既能消除冗余或无用属性对分类算法依赖的距离度量的影响，又能较好地消除邻居中的噪声点，从而提高算法的分类效果；侯玉婷等[7]则提出了一种自适应加权K-近邻分类方法，通过对不同特征分别进行加权，可以有效提高自然图像的分类性能。马氏距离[8-9]与欧氏距离相比较，它不受量纲的影响，并且可以反映样本间的差别。Zhang等[10]提出一种基于传统马氏距离的KNN算法(MKNN)，并通过实验验证了算法的优越性，但是马氏距离夸大了微小变量的作用。韩涵等[11]就此不足提出一种加权的马氏距离改进算法，并得到了较好的测试效果。此外，肖辉辉等[12]还定义2个样本间的距离为属性值的相关距离，以此距离来有效度量样本间的相似度，从而提高了算法的分类准确性。上述文献对KNN算法的距离度量做了各种改进，使该算法的分类效果得到一定程度的提高；但是它们考虑的是样本的总体分布，忽略了数据的局部内在几何结构特征。

在2003年，一种叫作局部保持投影[13-14](locality preserving projections，LPP)的无监督特征降维算法被提出。该算法备受关注，是一种特殊的线性流行学习方法，其显著特点就是在维数压缩的过程中充分利用数据的局部内在几何结构信息或流形结构特征。

针对KNN的上述问题，本文借鉴LPP的基本思想，提出了一种新颖的KNN算法。首先，根据类内局部保持散度矩阵构造了一种新的距离度量方式，然后利用该方式提出了局部保持K近邻算法(locality preservingK-nearest neighbor, LPKNN)。LPKNN采用新的距离度量方式，利用充分反映数据内在几何结构特征的类内局部保持散度矩阵；因此，相对于KNN和MKNN算法，LPKNN算法最显著的特点是充分考虑了每一类数据的内在几何结构信息，并且该方法利用数据的内在几何结构特征，不同于原始的LPP。LPP属于无监督方法，没有考虑数据的类别信息，而本文定义的类内局部保持散度矩阵使用了数据的类标，属于监督方法。实验结果显示，相对于KNN和MKNN，LPKNN表现出更好的分类精度。

1 相关准备工作

在本文内容中，假定有由M个样本组成的训练数据集X=[x1,…,xM]和N个样本组成的测试数据集Y=[y1,…,yN]， ∀xi,yj∈RP,X∈RP×M,Y∈RP×N。把训练数据集X划分到C个不同的类别，并用Xm表示第m(m=1,…,C)类数据子集，共包含Nm个样本。

1.1 KNN分类算法

KNN是模式识别非参数分类算法中最重要的方法之一。它的工作原理是首先找到待分类对象在训练数据集中的K个最近的邻居,然后根据这些邻居的分类属性进行投票,将得出的预测值赋给待分类对象的分类属性。欧氏距离和马氏距离是KNN算法中常见的距离度量。其计算公式为：

d(yi,xmj)2=(yi-xmj)T(yi-xmj)；

(1)

dM(yi,xmj)2=(yi-xmj)TS-1(yi-xmj)。

(2)

式中：S是训练数据集X的协方差矩阵；xmj表示的是第m(m=1,…,C)类数据子集Xm的第j个数据。

式(1)的欧氏距离是衡量多维空间中各个点之间的绝对距离，是最常用的距离。使用欧氏距离的分类算法大多只能发现低维空间中呈超球状分布的数据，它的缺点是将样品的不同属性之间的差别等同看待。式(2)的马氏距离与欧氏距离不同，它可以排除变量之间的相关性干扰，并且不受量纲的影响；但是它会夸大变化微小的变量的作用。

1.2局部保持投影

局部保持投影(LPP)算法是通过构造数据集所对应的k-近邻图来保持样本的局部内在几何结构信息。该算法是通过提取最具有判别性的特征来进行降维，因此在保留局部特征时具有明显的优势。设w为权值矩阵，a为投影向量，LPP的目标函数为

(3)

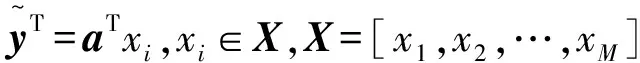
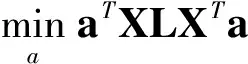
(4)

s.t.aTXDXTa=1。

(5)

其中D为对角矩阵，Dii=∑jWij(W为对称阵)，Dii越大，表示xi越重要。L=D-W,被称作拉普拉斯矩阵。约束式(5)是为了避免a=0这个解。投影矩阵a可以通过求解目标函数最小化的广义特征值问题对应的特征向量得到。

2 基于局部保持的KNN算法

2.1类内局部保持散度矩阵

本节给出了文献[15]中引出的相关概念。本文后续部分将直接使用这些定义。

定义1 假定L是定义在数据集X上的拉普拉斯矩阵，则把矩阵Z=XLXT=X(D-W)XT叫作数据集X上的局部保持散度矩阵。

定义2 假定数据集X含有C类数据集，则把矩阵

(6)

(7)

2.2基于局部保持的马氏距离

结合LPP算法的思想,利用类内局部保持散度矩阵,构造一个能够反映数据内在结构特征的新距离度量公式，为

dLP(yi,xmj)2=(yi-xmj)TZw-1(yi-xmj)。

(8)

其中Zw是训练数据集X上的类内局部保持散度矩阵。

根据前面的描述，可以明显的看出，欧氏距离、马氏距离与基于类内局部保持散度矩阵的马氏距离的不同。欧氏距离矩阵将所有特征间的差别平等对待，马氏距离矩阵仅考虑数据的分布信息，它们都忽略了其内部几何结构特征；而基于类内局部保持散度矩阵的马氏距离是借鉴LPP算法的基本思想进行定义的,相对于欧氏距离和传统马氏距离，它不仅保持了数据的内在几何结构特征还具有鉴别信息的作用。这也是它与LPP定义权值矩阵功能最大的不同。

2.3基于局部保持的KNN算法

式(8)定义的新距离度量能够反映每一类数据的局部内在几何结构特征，在本小节中,将该距离度量运用到KNN算法中，便得到本文提出的局部保持K近邻算法。

LPKNN算法的分类决策过程如下：对于一个给定的测试数据yi，分别计算它与训练数据集X中每一个训练数据的距离，找到与之最近的K(K≥1)个训练数据，其中属于第m类的数据有Km个，判别函数为

(9)

其中dLP(yi,xmj)为测试数据yi与训练数据xmj之间的距离，如式(8)所示。按式(10)决策测试数据yi属于第m类。

fm(yi)=arg max(gm(yi))。

(10)

通过上述分析，算法步骤简单描述如下。

Step1：计算测试数据集Y中对象yi与训练数据集X中每个对象的距离，距离度量公式采用式(8)。

Step2：找出yi与X中距离最近的K个对象。

Step3：依次统计出这K个对象的所属类别，找出包含最多个数的类。

Step4：将yi划分到此类中。

Step5：重复以上步骤，直到所有测试数据分类结束。

Step6：输出标志后的测试集Y。

这里，可以清晰地看出KNN、MKNN和LPKNN3种算法的不同。KNN算法直接采用欧氏距离矩阵，没有考虑数据的特征；MKNN算法采用基于数据协方差矩阵的马氏距离来利用数据的分布特征； LPKNN算法借鉴MKNN利用数据分布特征的方式，采用了基于类内局部保持散度矩阵的马氏距离，达到了充分考虑数据内在几何结构特征的目的，而且在LPKNN算法采用的类内局部保持散度矩阵中，利用了数据的类别信息。

2.4矩阵奇异问题

LPKNN算法和MKNN算法一样，最大的缺点就是会遇到一种所谓的小样本问题[16]，即样本的维数大于样本的个数。在运行这2种算法时，基于类内局部保持散度矩阵的马氏距离中的Zw和传统马氏距离中的协方差矩阵S都是P×P矩阵，都会出现奇异。除此之外，当样本维数小于样本个数时也可能会出现奇异。

为了解决矩阵奇异这个问题，可以采用以下几种方法：求矩阵Zw和S的伪逆矩阵；将矩阵Zw和S正则化；用特征降维算法PCA[17]将样本空间中的数据转换到低维空间中。这样矩阵Zw和S就不再是奇异的了。本文采用PCA特征降维算法来解决矩阵的奇异问题。

3 实验研究

为了验证LPKNN算法的可行性及分类效果，在实验中，将其与KNN和MKNN算法进行了比较。实验分为3部分：第1部分实验采用人工拟合数据进行测试；第2部分主要针对UCI(University of California，Irvine)[18]中的部分数据集进行测试；第3部分采用ORL人脸数据集进行测试。

3.1拟合数据

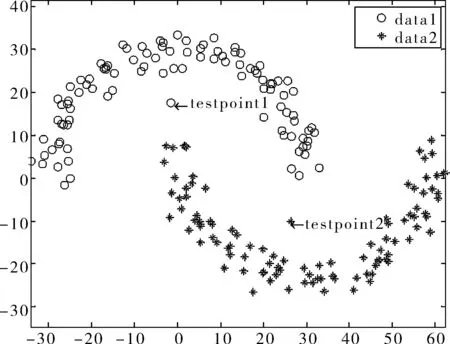
人工拟合数据由two moons数据集和2个测试点组成，two moons数据集具有明显非线性流行结构，如图1(a)所示。从理论上讲，欧式空间是线性的黎曼流行空间，而非线性黎曼流行空间是典型的非欧式空间，所以蕴含非线性流行结构的two moons数据集是非欧式空间[19]；因此，通过测试2个数据点属于two moons数据集的哪一类来表明本文算法在处理数据内在几何结构特征空间时的有效性。

图1给出了原始拟合数据以及该数据在k为3到10的范围内变化时3种算法下的测试结果。此外，LPKNN算法中的k-近邻参数为3，t-热内核参数为4。图1(a)是拟合的two moons数据集及2个测试点;图1(b)是KNN算法的测试结果;图1(c)是MKNN算法的测试结果;图1(d)是LPKNN算法的测试结果。

不难发现，在使用欧氏距离和传统马氏距离的KNN算法时testpoint1被分类给data1，testpoint2被分类给data2，而采用LPKNN算法时testpoint1被分类给data2，testpoint2被分类给data1。由观察数据可知，testpoint1被分类给data2和testpoint2被分类给data1是two moons数据集延伸的必然趋势，故更具合理性。这也证明了采用欧氏距离的KNN算法反映的是2点之间的绝对距离，采用传统马氏距离的KNN算法考虑的是数据的分布信息，它们都忽略了LPKNN算法中具有的数据的内在几何结构特征。

(a) two moons数据集及测试点

(b) KNN分类结果

(c) MKNN分类结果

(d) LPKNN分类结果

3.2 UCI数据

在这一部分的实验中，采用10个UCI数据来比较LPKNN与KNN和MKNN的分类性能。表1描述了这些数据的基本信息。

设定3种算法都有的近邻参数K=5。此外，在LPKNN算法中需要构造权值矩阵Wm，其中的参数k、t的变化范围分别为{3,4,5,6,7,8,9,10}和{0.25,0.5,1,2,4,8,16,32}。采用5重交叉测试[20](5-fold cross validation)来进行参数选择。5重交叉测试就是把所有的训练数据随机地分成5个互不相交的子集，每个子集的大小大致相等，然后进行5次训练测试，最后计算出这5次训练测试的平均精度,并将其作为参数选择的评估准则。

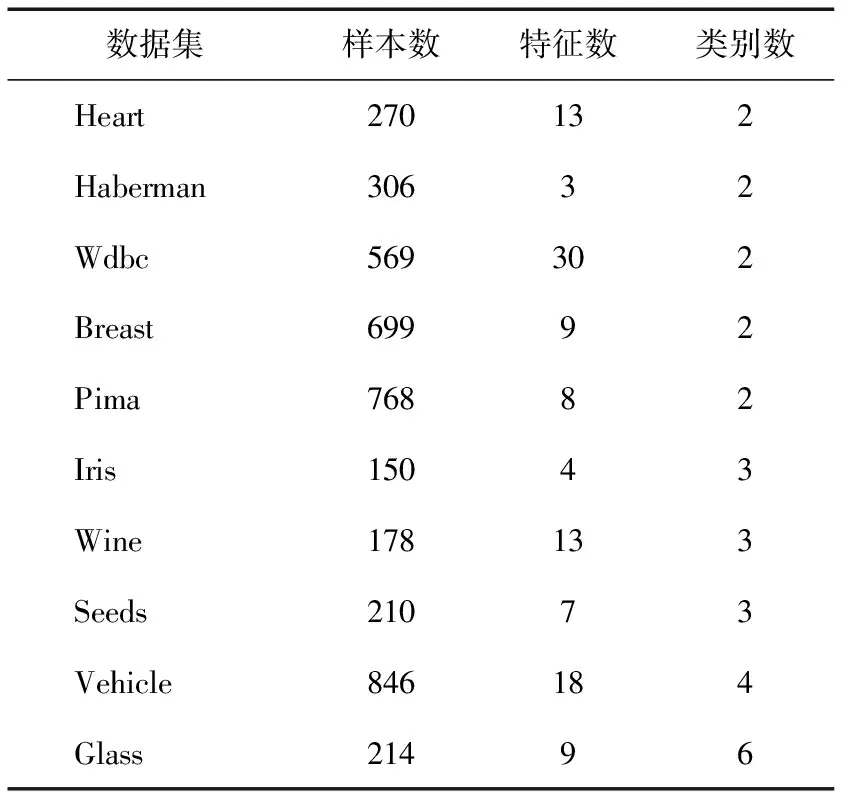
表1 实验中UCI数据集的基本信息

实验中，随机选取数据的80%作为训练数据，剩下的作为测试数据。首先把训练数据的每一维特征处理成均值为0，方差为1，再根据同样的规则处理测试数据；然后将训练数据进行5重交叉测试；最后利用得到的参数对训练和测试数据进行实验。重复该过程20次,并把所得分类精度的平均值作为算法的评价指标。UCI数据集上20次测试的平均精度和标准偏差在表2中给出。

表2 UCI数据集上20次测试的平均精度和标准偏差 %

从这些实验结果可以看出，总体上LPKNN都表现出了比KNN和MKNN更好的分类效果，这说明当充分利用了每一类数据的局部内在几何结构信息时，有利于提高算法的分类精度。尽管MKNN考虑了数据的分布信息，但是相对于KNN的实验结果，在大多数情况下的分类精度都表现得更低。这可能是由于数据的分布特征造成的。

3.3人脸数据

为了测试在小样本情况下LPKNN算法的分类效果，在这一部分的实验中采用ORL人脸数据来进行实验研究。ORL人脸数据包括40个人共400张灰度图片，每人有10张分辨率为32×32的人脸图像。ORL处理后的matlab数据可从http://www.cad.zju.edu.cn/home/dengcai/Data/FaceData.html处下载。图2为经过预处理后的部分人脸图像。测试之前所有的数据都被归一化为0到1之间。

图2 ORL预处理后的部分人脸图像

由于是小样本数据，MKNN算法和LPKNN算法都分别遭遇了协方差矩阵S和类内局部保持散度矩阵Zw的奇异性问题，因此采用PCA降维算法来对数据进行维数压缩，在压缩后的数据空间中运行这2种算法。KNN算法则不存在这样的问题。

由于人脸数据每一类的样本个数较少，因此，设定3种算法都有的近邻参数K=1。对于LPKNN中权值矩阵Wm的参数k、t的变化范围分别是{3,4,5,6}和{5,10,20,30,40}。同样采用5重交叉测试进行参数选择。实验中，首先随机选取数据的80%作为训练数据，其余为测试数据；然后将训练数据进行5重交叉测试；最后对训练和测试数据进行实验。此过程也重复20次，将分类精度的平均值作为算法的评价指标。表3给出了不同维数下ORL数据的测试结果，同时给出了采用KNN算法直接在样本空间或特征空间中进行测试的结果。

表3 ORL人脸数据上5重交叉测试的平均精度和标准偏差 %

从这些实验结果中可以看出： 1)在每一维上LPKNN算法比KNN和MKNN都体现出了更好的分类精度且随着维数增加分类精度逐渐提高，这说明考虑了数据内在几何结构特征的算法改进了实验的结果； 2)采用PCA降维后，算法的分类精度有了一定程度的提高，这是由于PCA在进行维数压缩时可能会去掉数据特征中的噪声,但是如果维数被压缩得太低也会损失数据中有用的鉴别信息； 3)一般情况下当把数据投影到(1/5)×d维(d为特征维数)空间时3种算法都是可逆的，而此时LPKNN算法的分类精度比降维和不降维的KNN算法都有大幅度的提高，这也说明了充分利用每一类数据的内在几何结构信息，有利于提高算法的分类精度。

4 结束语

本文借鉴LPP算法的基本思想提出了一种局部保持K近邻算法。不同于基于欧氏距离和传统马氏距离的KNN，LPKNN不仅考虑到了数据内在几何结构特征还能够鉴别数据信息，表现出了更好的分类精度。针对LPKNN和MKNN都遭遇的小样本问题，本文采用PCA将原始空间的数据转换到低维空间来解决。实验结果表明，该算法比基于欧氏距离和传统马氏距离的KNN算法的分类精度都有所提高，说明充分利用数据的内在几何结构信息有利于提高算法的分类精度；但是在运行LPKNN算法的时候由于进行参数选择会花费较多的时间，因此如何提高算法的速度将是今后工作的研究方向。

[1]Cover T M, Hart P E. Nearest Neighbor Pattern Classification[J]. IEEE Transactions on Information Theory, 1967, 13(1):21-27.

[2]刘博,杨柳,袁方. 改进的KNN方法及其在中文文本分类中的应用[J]. 西华大学学报：自然科学版,2008,27(2):33-36.

[3]沈媛媛, 严严, 王菡子. 有监督的距离度量学习算法研究进展[J]. 自动化学报, 2014, 40(12):2673-2686.

[4]王骏, 王士同, 邓赵红. 聚类分析研究中的若干问题[J]. 控制与决策, 2012, 27(3):321-328.

[5]Jing Yinan, Hu Ling, Ku Wei-Shinn, et al. Authentication of k Nearest Neighbor Query on Road Networks[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(6):1494-1506.

[6]卢伟胜, 郭躬德, 严宣辉，等. SMwKnn:基于类别子空间距离加权的互k近邻算法[J].计算机科学, 2014, 41(2):166-169.

[7]侯玉婷, 彭进业, 郝露微，等. 基于KNN的特征自适应加权自然图像分类研究[J]. 计算机应用研究, 2014, 31(3):957-960.

[8]Shen Chunhua, Kim J, Wang Lei. Scalable Large-Margin Mahalanobis Distance Metric Learning[J]. IEEE Transactions on Neural Networks, 2010, 21(9):1524-1530.

[9]Washizawa Y, Hotta S. Mahalanobis Distance on Extended Grassmann Manifolds for Variational Pattern Analysis[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(11):1980-1990.

[10]Zhang Suli, Pan Xin. A novel Text Classification Based on Mahalanobis distance[C]//Proceedings of the 2011 3rd International Conference on Computer Research and Development. China:IEEE, 2011:156-158.

[11]韩涵, 王厚军, 龙兵，等. 基于改进马氏距离的模拟电路故障诊断方法[J]. 控制与决策, 2013, 28(11): 1713-1717.

[12]肖辉辉, 段艳明. 基于属性值相关距离的KNN算法的改进研究[J]. 计算机科学, 2013, 40(11A):157-159.

[13]Kokiopoulou E, Saad Y. Orthogonal Neighborhood Preserving Projections: A Projection-Based Dimensionality Reduction Technique[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29 (12) :2143-2156.

[14]Silva E R, Cavalcanti G D C, Ren T I.Class-Dependent Locality Preserving Projections for Multimodal Scenarios[C]// Proceedings of the IEEE 24th International Conference on Tools with Artificial Intelligence. Greece:IEEE, 2012:982-987.

[15]Wang Xiaoming, Chung Fu-lai, Wang Shitong. On Minimum Class Locality Preserving Variance Support Vector Machine[J]．Pattern Recognition, 20l0, 43(8):2753-2762.

[16]Liu Jixin, Khemmar R, Ertaud J Y, et al. Compressed Sensing Face Recognition Method in Heterogeneous Database with Small Sample Size Problem[C]// Proceedings of the 2012 Eighth International Conference on Signal Image Technology and Internet Based Systems. Italy:IEEE, 2012:80-84.

[17]张学工. 模式识别[M]. 3版. 北京:清华大学出版社, 2010:163-165.

[18]Newman D J, Hettich S,Blake C L, et al.UCI Repository of Machine Learning Databases[EB/OL]. [2014-12-25]. http://www.ics.uci.edu/～mlearn/MLRepository.html.

[19]王珏, 周志华, 周傲英. 机器学习及其应用[M]. 北京: 清华大学出版社, 2006:135-164.

[20]Abril L G, Angulo C, Velasco F, et al. A Note on the Bias in SVM for Multiclassification[J]. IEEE Transanctions on Neural Netwoks, 2008, 19(4):723-725.

(编校：饶莉)

KNNAlgorithmBasedonLocalityPreserving

ZENG Jun-jie, WANG Xiao-ming*, YANG Xiao-huan

(SchoolofComputerandSoftwareEngineering,XihuaUniversity,Chengdu610039China)

The distance metric plays an important role inK-nearest neighbor(KNN) algorithm. The traditional KNN algorithm usually employs the Euclidean distance. However, this distance treats all features equally and ignores the local intrinsic geometric structural characteristics of data. In this paper, following the basic idea of locality preserving projection(LPP), we firstly used the locality preserving within-class scatter matrix to propose a novel distance metric, then we developed a modified version of KNN called locality preservingK-nearest neighbor(LPKNN). The proposed method takes the local intrinsic geometric structural characteristics of data into full consideration. The experimental results indicate that the proposed algorithm can obtain higher classification accuracy in contrast with the KNN algorithm based on the Euclidean distance and the traditional Mahalanobis distance.

K-nearest neighbor; locality preserving projection; Mahalanobis distance

2014-12-30

国家自然科学基金项目(61103168)；四川省教育厅自然科学重点项目(11ZA004)；西华大学研究生创新基金项目(ycjj2014032)。

：王晓明(1977—)，男，副教授，博士，主要研究方向为模式识别、图像处理。E-mail:392805710@qq.com

TP18；TP391.1

：A

：1673-159X(2015)06-0058-06

10.3969/j.issn.1673-159X.2015.06.012

*