基于椭球模型的岩坡稳定非概率可靠评价研究

(南京水利科学研究院，江苏 南京 210098)

·建筑与土木工程·

基于椭球模型的岩坡稳定非概率可靠评价研究

韩孝峰，陈海军

(南京水利科学研究院，江苏 南京 210098)

在考虑影响因素的不确定性条件下，快速有效地评价岩坡的稳定状态成为目前研究的热点。传统概率可靠方法评价要求数据充足且服从某种概率分布，工程中难以实测大量数据支持，从而阻碍了该方法的推广应用。本文针对以上不足，结合平面滑动型岩坡在只需确定变化范围的前提下应用椭球模型表达不确定影响因素的变异性质，采用相应的非概率可靠指标评价了岩石边坡的稳定状态，与蒙特卡洛模拟法计算结果的对比显示两种评价结果一致。基于椭球模型的非概率可靠评价方法所需数据量小，计算简便快捷，在岩坡稳定问题的评价中具有一定的适用性。

椭球模型；非概率可靠；岩石边坡；稳定性评价；蒙特卡洛模拟

随着我国经济建设的发展，各大工程领域中都会涉及到岩石边坡稳定问题[1]。岩坡的安全稳定对工程具有不小影响，快速准确地评价岩坡的稳定性很重要。实际工程中，岩坡稳定影响因素的取值往往不是一个固定值。在分析岩坡稳定问题的定性分析、定量分析和不确定可靠分析这3大类方法中[2]，不确定可靠分析方法能够考虑影响因素的随机变异特点[3]；但目前运用较多的概率不确定可靠性分析方法对岩坡稳定进行分析评价时，需要明确各个影响参数的统计概率分布规律[4]。这在实际工况中是无法实现的，若采用小样本的概率分布模型计算，则会出现较大偏差，影响评价结果。针对以上存在的问题，本文将椭球模型与可靠性分析原理相结合，建立一种在数据不足、样本数目很小的情况下也能评价岩石边坡稳定性的方法，该评价方法有别于传统概率分析方法，可划入非概率可靠分析方法范畴中。由于该方法不用建立影响因素的概率分布，使计算量得到缩减，可十分快速地得到评价结果。结合经典算例评价，并与蒙特卡洛模拟结果进行对比，显示评价结果十分准确。

1 不确定参数的椭球表达

椭球模型能够准确地表达出不确定参数的变化特点。在岩坡稳定分析问题中，不确定参数指的就是影响边坡稳定的因素。椭球模型用来表达岩坡稳定影响因素变化性质时，可以看作是每个影响参数不同取值的组合。从几何上看，椭球模型具有独特的形状和尺度，形状反映了该模型对不确定参数的已知程度，尺度反映了不确定参数的偏离程度[5]。

假设存在n个不确定的参数，用X∈Rn表示不确定参数可能取值组成的向量。椭球模型用一个超椭球体来界定n个不确定参数，可用下式表达：

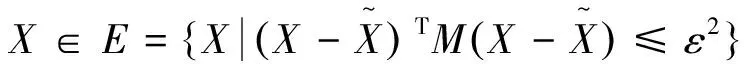
(1)

2 基于椭球模型的非概率可靠性分析方法的建立

2.1可靠性分析理论

结构分析的核心思想是使结构在使用期限内能够满足安全性、适用性和耐久性等3个方面的要求[6]，结构的可靠指的是满足上述3项要求。结构的可靠性程度一般用可靠度来定量描述。结构的可靠性往往受到各种外部荷载、内部介质强度以及结构自身几何尺寸等因素的影响，这些因素往往是在一定范围内变化且其变化规律具有不确定性。可靠性分析中称这些影响结构可靠性的因素为基本变量[7]，即对应岩坡稳定问题中提到的各个影响因素。设Xi,i=1,2,…,n为结构的n个基本变量，则结构安全状态的功能函数可用基本变量的复合函数来表示：

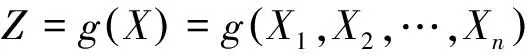
(2)

上式是结构基本变量的复合函数，这一函数表示了结构可靠性的状态，随着基本变量组合的不同，其表达的可靠性状态也不一样。结构系统是否可靠取决于结构的可靠性状态，结构的可靠性状态是用其功能函数的大小来表示的：

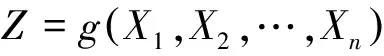
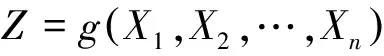
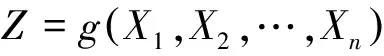
2.2基于椭球模型的非概率可靠指标

将椭球模型表达的不确定参数应用于可靠分析理论中可获得如下评判方法。在标准化平面中，椭球模型表示的是一个平面椭球形，如图1所示。

该坐标系中，基本变量的边界可用‖Q‖2=1来表示，即图中的单位圆。基本变量的组合点都位于单位圆区域以内，极限状态曲线将平面划分为安全域和失效域。

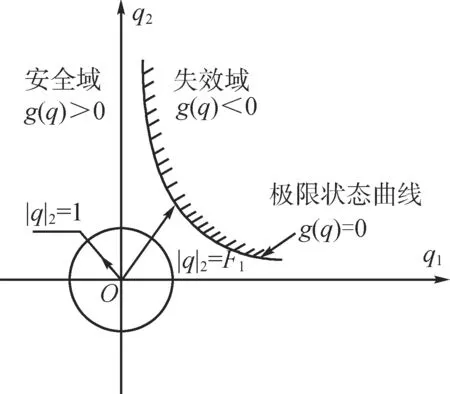
图1 椭球模型下的非概率可靠性度量

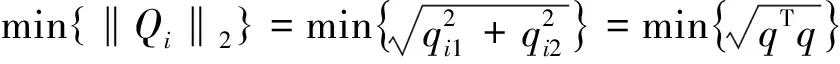
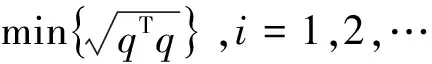
(3)

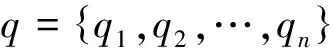
根据以上定义，基于椭球模型的非概率可靠性指标取值可以为任意实数。结合可靠性分析理论，当η≥1时，结构的基本变量取值都位于安全域内，此时结构完全可靠。当-1<η<1时，基本变量的组合点有部分落在安全域内，也有部分落在失效域内，此时结构存在可靠风险；但在该区间内，结构的可靠性随着η的增大而增大。当η<-1时，基本变量的组合点全部落在失效域内，此时的结构完全不可靠，对于岩坡稳定问题来说指的就是发生滑坡。

2.3岩坡稳定问题基于椭球模型的非概率可靠分析步骤

对岩坡稳定问题进行非概率可靠性分析的具体步骤如图2所示。

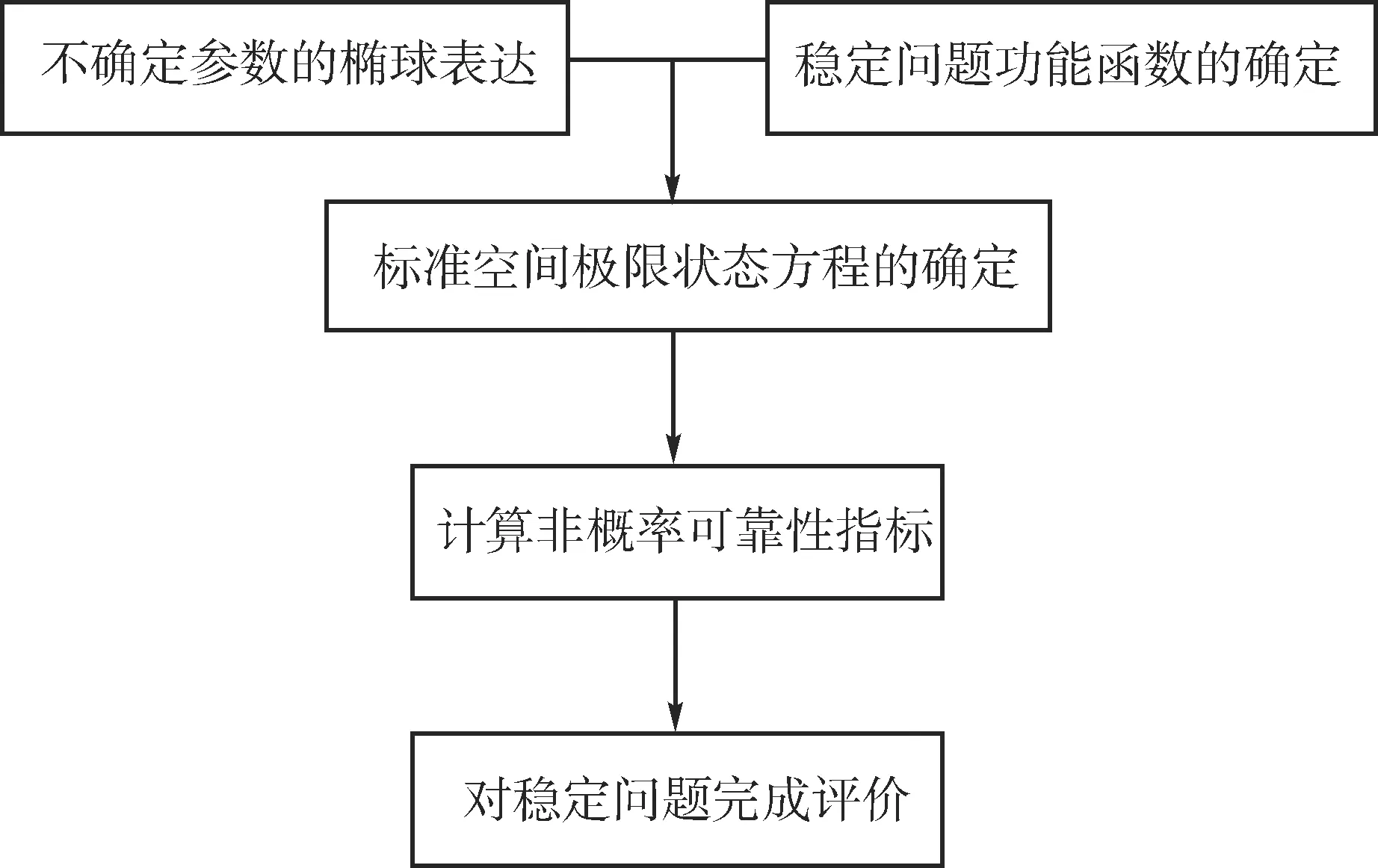
图2 岩坡稳定问题基于椭球模型的非概率可靠性分析步骤图

3 应用算例

3.1计算模型的选取

本文选取经典的二维岩石边坡计算模型[8]，具有一定的代表性。该岩坡模型中存在一组软弱结构面，假设岩坡发生破坏时的滑动面与该结构面重合，发生平面型滑动破坏，如图3所示。该岩坡模型一旦发生破坏，上部滑体沿结构面下滑，坡顶后缘受拉产生张拉裂缝，裂缝会充水。从图中可以看出该计算模型存在着以下几何特征：

(4)

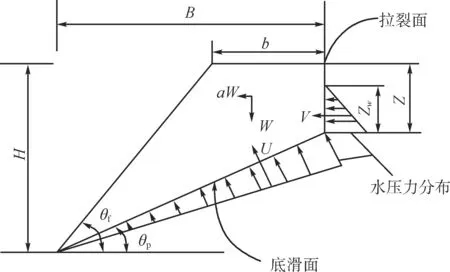
图3 岩石边坡示意图

以上一些参数取值如表1所示，边坡宽度取单位宽度[8]。

表1 岩石边坡参数取值表

本文在进行非概率可靠评价的基础上，同时采用了蒙特卡洛模拟对该岩坡的稳定性能进行计算，旨在对比2种方法的结果是否一致。

为了更清晰地对比2种方法的评价效果，计算过程中分别考虑了有水平地震力和无水平地震力2种情况下，该岩石边坡的稳定状态。

3.2岩坡平面滑动问题的椭球模型非概率可靠性分析

3.2.1 岩石边坡稳定性不确定参数的椭球模型

该岩石边坡的2个不确定参数选取为潜在滑动面的黏聚力及内摩擦角，它们的取值均服从标准正态分布，如表2所示[8]。

表2 岩石边坡不确定参数取值分布

值得一提的是，上述2个参数的标准正态分布是在进行蒙特卡洛模拟时才需用到，而采用椭球模型表达时只需知道参数的变化范围。这2个基本变量可用椭球模型表示为

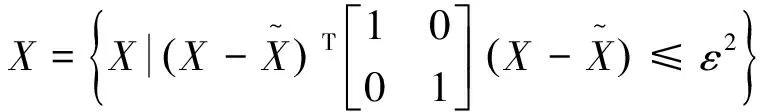
(5)

3.2.2 功能函数的确定

岩坡沿潜在滑动面的抗滑力大于下滑力时，岩坡能保持稳定状态。岩坡的功能函数可以表达为

Z=R-S。

(6)

其中：R表示岩石边坡的抗滑力；S表示岩石边坡的下滑力。

1)不考虑水平地震作用。

对图3的岩石边坡模型进行受力分析，下滑力S的表达式为

S=Wsinθp+Vcosθp。

(7)

抗滑力R的表达式为

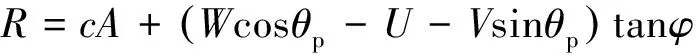
(8)

整理可得该坡稳定性能所对应的功能函数为

Z=12 711tanφ+70c-11 962。

(9)

2)考虑水平地震作用。

地震作用简化为施加在物体上的一个水平惯性力。设水平地震加速度的取值在0～0.4之间。

相应功能函数可表达为

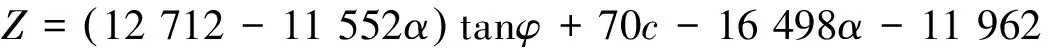
(10)

3.2.3 非概率可靠性指标的计算

1)不考虑水平地震作用。

岩坡稳定功能函数可标准化为

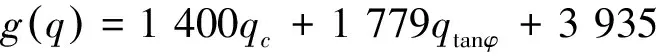
(11)

采用直接迭代法求得椭球模型非概率可靠性指标为1.745 7，迭代曲线如图4所示。该指标值表明岩石边坡稳定状态可靠。从曲线看出仅用了2步迭代就得到了接近精确解的值。

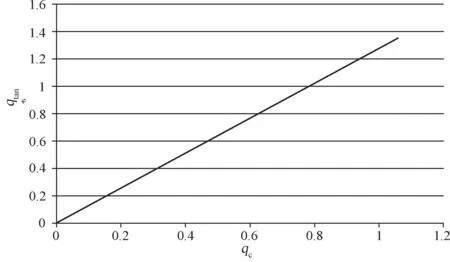
图4无水平地震作用下岩坡稳定非概率可靠指标迭代历史

2)考虑水平地震作用。

考虑地震作用产生的水平力时，岩坡稳定可靠性对应的功能函数可标准化为

323qαqtanφ+2 319。

(12)

采用迭代法可快速计算出非概率可靠性指标为0.439 2，过程如表3所示。此时岩坡稳定不可靠。

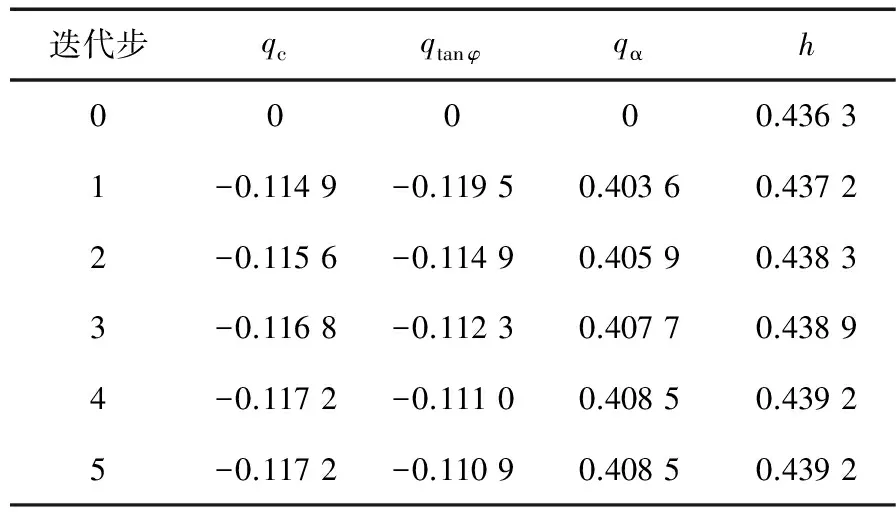
表3 水平地震作用下岩坡稳定非概率可靠指标迭代历史

通过迭代计算出的可靠性指标，不难看出地震作用对岩坡稳定可靠性的影响极其明显。在水平地震作用下，该岩坡的稳定状态不可靠，存在失稳破坏的风险。

3.3岩坡平面滑动问题的Monte Carlo模拟法

蒙特卡洛模拟法能达到的精度与样本数量存在必然的联系，是目前概率可靠分析中较精确的方法。采用该方法的前提是要掌握有关参数的大量实测值以确定该参数的概率分布，否则蒙特卡洛模拟无法进行。

3.3.1 不考虑水平地震作用

不考虑水平地震作用时，蒙特卡洛模拟中的随机变量为软弱结构面的黏聚力和内摩擦角，它们的均值和方差见表2。

图5为岩坡安全系数的累积密度分布图，图中与横坐标安全系数为1时所对应的纵坐标值大约为0.02，表明该岩石边坡的失效概率不到2%。

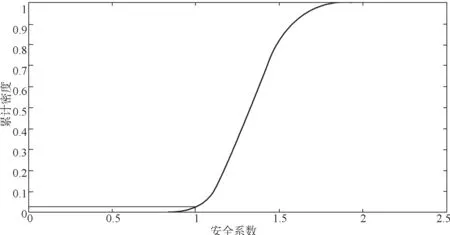
图5 无地震作用下岩坡安全系数累积概率密度分布图

3.3.2 考虑水平地震作用

考虑水平地震作用时，随机变量增加一个水平地震加速度。图6为岩坡安全系数的累积密度分布图，图中与横坐标安全系数为1时所对应的纵坐标值大约为0.31左右，表明该岩坡的失效概率为31%左右。

蒙特卡洛模拟计算的结果表明该岩石边坡在不受水平地震作用时的稳定状态很好，失效概率不到2%，在受水平地震作用时其稳定失效概率会增至31%左右。

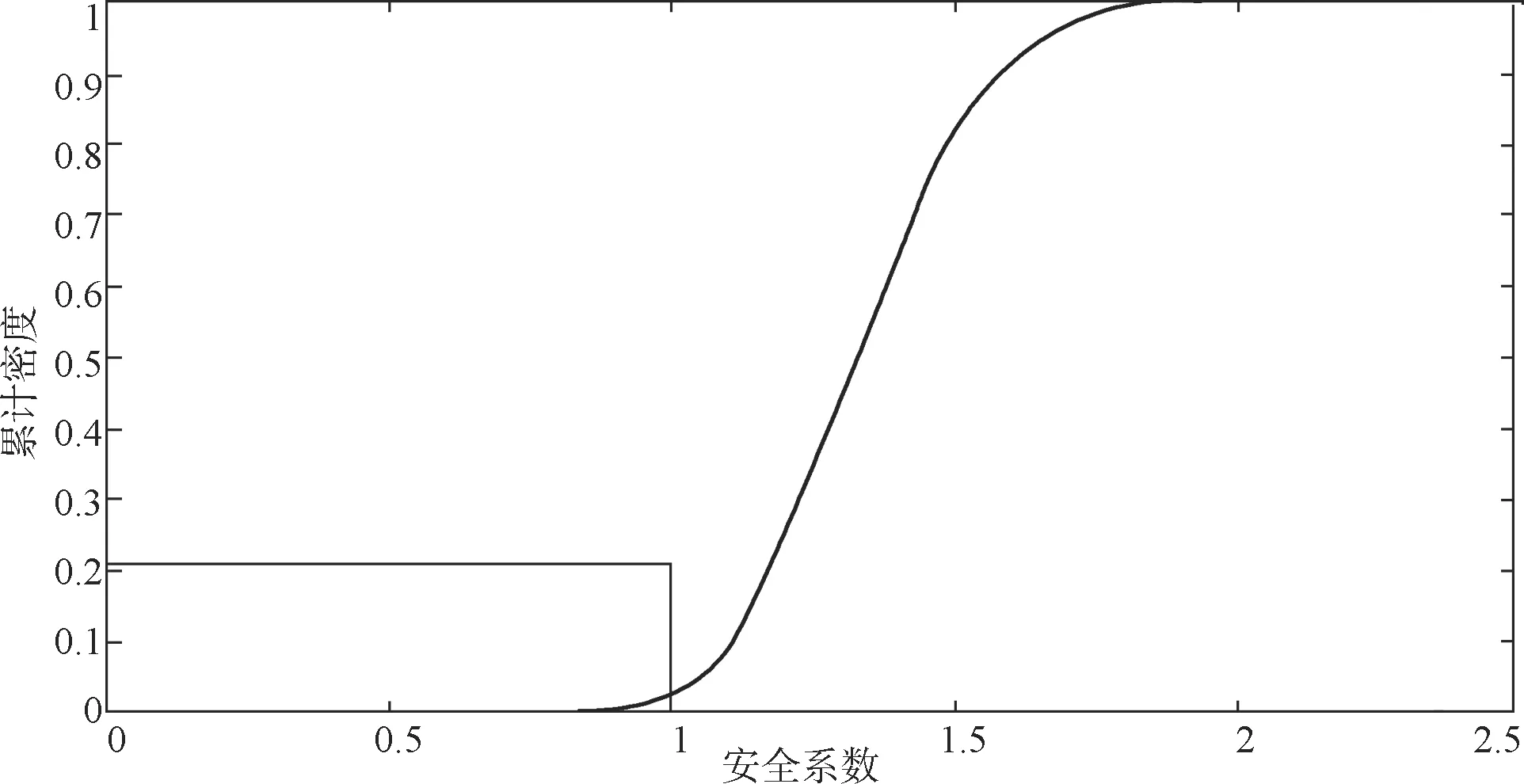
图6 地震作用下岩坡安全系数累积概率密度分布图

3.4结果讨论

通过对2种方法的计算结果进行对比可以看出：

1)对于本文选取的岩石边坡计算模型，在无水平地震作用时，基于椭球模型的非概率可靠性分析方法结果为该岩石边坡稳定状态可靠。通过蒙特卡洛模拟计算得出该岩石边坡的失效概率不到2%，该岩坡几乎不会破坏。在有水平地震作用下，基于椭球模型非概率可靠性分析结果表明岩石边坡稳定状态不可靠。此时采用蒙特卡洛方法计算得出岩石边坡的失效概率高达31%，该岩坡存在很大的破坏风险。

2)考虑水平地震作用和未考虑水平地震作用这2种情况下，基于椭球模型的非概率可靠性分析结果和蒙特卡洛模拟法计算结果对岩坡稳定状态的评价保持一致。

3)蒙特卡洛模拟法计算时需要随机变量的概率分布，且计算耗时较长，而基于椭球模型的非概率可靠性分析方法只需明确随机变量的变化范围且迭代计算过程较快。

4 结论

本文在总结国内外有关岩坡稳定分析、椭球模型理论及可靠性分析研究现状[2-10]的基础上，开展了将基于椭球模型的非概率可靠性分析方法应用于岩坡稳定问题评价的研究工作。结合经典的岩石边坡模型，建立不确定参数的椭球模型表达，采用相应的非概率指标计算方法，利用计算结果评价分析了岩石边坡的稳定状态，并通过与现已成熟的蒙特卡洛模拟法结果进行对比，验证了该评价方法在岩坡稳定问题中的适用性。得到以下结论：

1)基于椭球模型的非概率可靠性分析方法评价岩坡稳定问题时，仅需知道不确定参数的变化范围，避免了传统概率可靠性分析时必须确定参数数学概率分布的限制条件，使计算简便快捷。

2)在对样本数据量要求不高的前提下，本文方法计算出的可靠性指标值与蒙特卡洛模拟法利用不确定参数的概率分布计算出的失效概率对评价平面滑动型岩坡稳定状态的意义保持一致，具备对岩石边坡稳定状态的评价功能。

[1]张俊云.岩石边坡植被护坡系统的水分平衡及控制[J].岩石力学与工程学报 ,2013(9):1729-1735.

[2]刘章军,陈飞,周宜红，等.岩质路堑深边坡稳定性评价的模糊概率方法[J].岩土力学,2008,29(增刊1):368-372.

[3]刘晓,唐辉明,熊承仁，等.边坡动力可靠性分析方法的模式、问题与发展趋势[J].岩土力学,2013(5):1217-1234.

[4]Johari A,Javadi A A. Reliability Assessment of Infinite Slope Stability Using the Jointly Distributed Random Variables Method[J]. Scientia Iranica,2012,19(3):423-429.

[5]罗阳军,亢战,Alex Li,等.基于凸模型的结构非概率可靠性指标及其求解方法研究[J].固体力学学报,2011,32(6):646-654.

[6]姜潮,刘丽新,龙湘云,等.一种概率-区间混合结构可靠性的高效计算方法[J].计算力学学报 ,2013(5):605-609.

[7]赵凯.土质边坡稳定性的可靠度研究[D].西安：西安理工大学,2013.

[8]李典庆,周创兵,陈益峰，等.边坡可靠度分析的随机响应面法及程序实现[J].岩石力学与工程学报,2010,29(8):1513-1523.

[9]陈帆，刘立，陆海空，等.岩质高陡边坡稳定性分析[J].西华大学学报：自然科学版，2010，29(3)：54-55.

[10]王玉平，曾志强，潘树林.边坡稳定性分析方法综述[J].西华大学学报：自然科学版，2012，31(2)：101-105.

(编校：叶超)

Non-probabilisticReliabilityAnalysisBasedontheEllipsoidalModelofRockSlopeStability

HAN Xiao-feng， CHEN Hai-jun

(NanjingHydraulicResearchInstitute，Nanjing210098China)

For evaluating the slopes’ stability accurately and quickly, non-probabilistic reliability based on the ellipsoidal model is used to overcome the existing disadvantages. Firstly, uncertain parameters are considered via the ellipsoidal model of the rock slope. And then the corresponding methods are used to calculate the non-probabilistic reliability index to evaluate the slope’s stability. Finally, the Monte-Carlo simulation were carried out to evaluate the rock slope’s stability as a comparison. The result shows that the non-probabilistic reliability analysis is more efficient and applicable.

ellipsoidal model；non-probabilistic reliability；rock slope；stability analysis；Monte-Carlo simulation

2014-11-10

中央级公益性科研院所基本科研业务费重点基金项目(Y313011)；江苏省科技支撑计划项目(BE2011373)

韩孝峰(1989—)，男，工程师，硕士，主要研究方向为结构体系可靠性分析、软土地基处理等。

*通信作者：陈海军(1973—)，男，教授级高级工程师，注册咨询工程师，博士，主要研究方向为工程地质及岩土工程。E-mail：hjchen@nhri.cn

TB114.3;TP18

：A

：1673-159X(2015)06-0096-05

10.3969/j.issn.1673-159X.2015.06.020