螺旋离心泵的双向流固耦合分析

刘 宜,2，白茂宁，程效锐,2，贾程莉

(1.兰州理工大学能源与动力工程学院，甘肃 兰州 7300502；2. 甘肃省流体机械及系统重点实验室，甘肃 兰州 730050))

·能源与环境·

螺旋离心泵的双向流固耦合分析

刘 宜1,2，白茂宁1，程效锐1,2，贾程莉1

(1.兰州理工大学能源与动力工程学院，甘肃 兰州 7300502；2. 甘肃省流体机械及系统重点实验室，甘肃 兰州 730050))

基于Reynolds时均化N-S方程、标准k-ε两方程湍流模型，以及结构响应的弹性体结构动力学方程，采用多重坐标系法，对螺旋离心泵清水介质时的内流场和结构动力学进行双向流固耦合全三维数值计算, 将计算结果与非流固耦合计算流场进行对比，分析流固耦合作用对泵外特性及不同叶轮位置泵内压力场和速度场的影响。结果表明：采用双向流固耦合模式的扬程和效率预测值更接近试验值；在小流量下流固耦合作用对外特性的影响较大，而在大流量下对外特性影响较小；流固耦合作用对压力场和速度场的影响主要集中在蜗壳扩散段，对蜗壳其他部位和叶片影响较小；在两种计算模式下蜗壳中截面压力分布出现明显差别，并在叶片出口正对隔舌时压力分布出现突变。

螺旋离心泵； 双向流固耦合； 数值计算； 流场； 外特性

螺旋离心泵是一种无堵塞泵，其叶轮是半开式的螺旋型结构，利用螺旋推进和离心作用输送介质[1-3]。其独特结构在输送固液两相流介质时具有高效率、无堵塞、对物料的破坏性小等优点，且功率曲线平坦，一般无过载问题[4-6]。

传统的流体机械研究方法主要是通过对流体机械过流部件进行简化的静力分析，忽略了流固耦合作用对流体机械的影响[7]。但离心泵内部流体与叶轮之间存在着相互作用：一方面，叶轮在流体压力载荷的作用下会产生变形和动力学响应；另一方面，叶轮反过来会影响流场的分布，进而改变流体载荷的分布和大小。 如果将流体域与结构单独求解而不考虑二者的相互作用，可能导致内部流场分析结果与实际流场不相符[8-9]。进入20世纪90年代，流固耦合分析被逐步应用到流体机械研究领域，其中水轮机领域的研究相对较多，但在泵领域的研究成果非常有限[10-12]。

本文以150×100LN-32型螺旋离心泵为研究对象，借助CFD软件CFX14.5及有限元分析软件ANSYS Workbench对该泵分别进行了非流固耦合和双向流固耦合数值计算，并对2种数值计算模式的外特性及不同叶轮位置压力场和速度场进行对比研究，分析流固耦合作用对螺旋离心泵内部流动的影响，为螺旋离心泵的运行和设计提供一定理论依据。

1 计算模型

1.1模型参数

所选模型为150×100LN-32型单叶片螺旋离心泵，其结构如图1所示，其设计参数如表1所示，叶轮主要设计参数如表2所示。

图1 螺旋离心泵结构图

表1 螺旋离心泵设计参数

流量qV/(m3/h)扬程H/m转速n/(r·min-1)效率η/%比转速ns1653214806285．2

表2 叶轮主要几何参数

1.2三维造型和网格划分

分别对螺旋离心泵全流道流场计算域和转子部件固体计算域进行三维建模，考虑到计算精度，同时兼顾计算工作量，对泵结构做了合理简化，忽略键槽、轴头螺母等部件，去除了叶轮远端轴承的轴段，叶轮和轴材料均为45钢，其材料基本特性如表3所示。

表3 转子材料特性参数

对螺旋离心泵的流体域和固体域分别采用有限体积法和有限元法进行网格划分，将流体域和固体域模型分别导入ICEM和ANSYS Workbench的Transient Structure模块中，采用不同尺度对网格进行划分。由于螺旋离心泵的叶轮结构特殊，叶片边缘存在一些尖角区域，所以流体域和固体域均采用自适应性较好的非结构化四面体网格进行离散，并对叶片和隔舌等重要部位进行局部加密处理，最终流体域网格总数为121万2 342，固体域网格总数为9万2 653，划分结果如图2所示。

(a)流体域网格 (b)固体域网格

图2 计算域网格划分

2 数值计算

2.1流体域控制方程

对于离心泵内部流场的计算，本文采用雷诺时均N-S方程，为了封闭流场求解的方程，必须建立湍流模型[13]。本文的螺旋离心泵输送介质为清水，根据已有研究成果，采用标准k-ε湍流模型[14]，该模型的控制方程组如下：

连续性方程

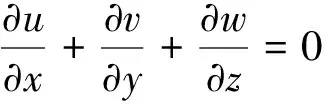
(1)

动量方程

(2)

式中：ρ为液体密度；ui、uj为雷诺时均速度；p为雷诺时均静压；ui′、uj′为脉动量；υ为运动黏性系数；xi、xj为笛卡尔坐标系坐标变量。

与湍动能、耗散率对应的运输方程为：

(3)

(4)

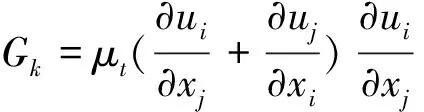
2.2固体域控制方程

泵在运行过程中，由于流体压力分布不均匀且有时域特性，叶轮会受到交变载荷的作用产生响应。在系统结构上每一时刻都承受自身内力和外力作用。运用有限元方法进行分析的系统运动微分方程[15]为

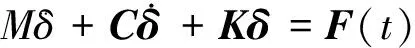
(5)

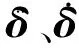
2.3数值计算方法

耦合计算采用双向流固耦合方法，将流体域和固体域模块进行交叉迭代耦合求解。对于固体域，将叶片工作面、背面、轮毂、顶面设置为互传递数据流固耦合面(fluidsolidinterface)，在轴承与转轴的结合面上添加圆柱约束，限制转子在x、y、z上的位移，同时在两轴承间的轴段上添加转速为1 480r/min旋转载荷，如图3所示。设置时间步长为 335μs(叶轮旋转3°)。对于流体域，设定速度进口与自由出流边界条件，壁面条件设置为无滑移壁面，湍流模型选用标准k-ε模型，近壁面选用scalable壁面函数。不同工况的设置通过给定不同进口速度计算，本文分别对0.4 、0.6 、0.8 、1.0 、1.2 、1.4 qV流量时的流动进行数值模拟。

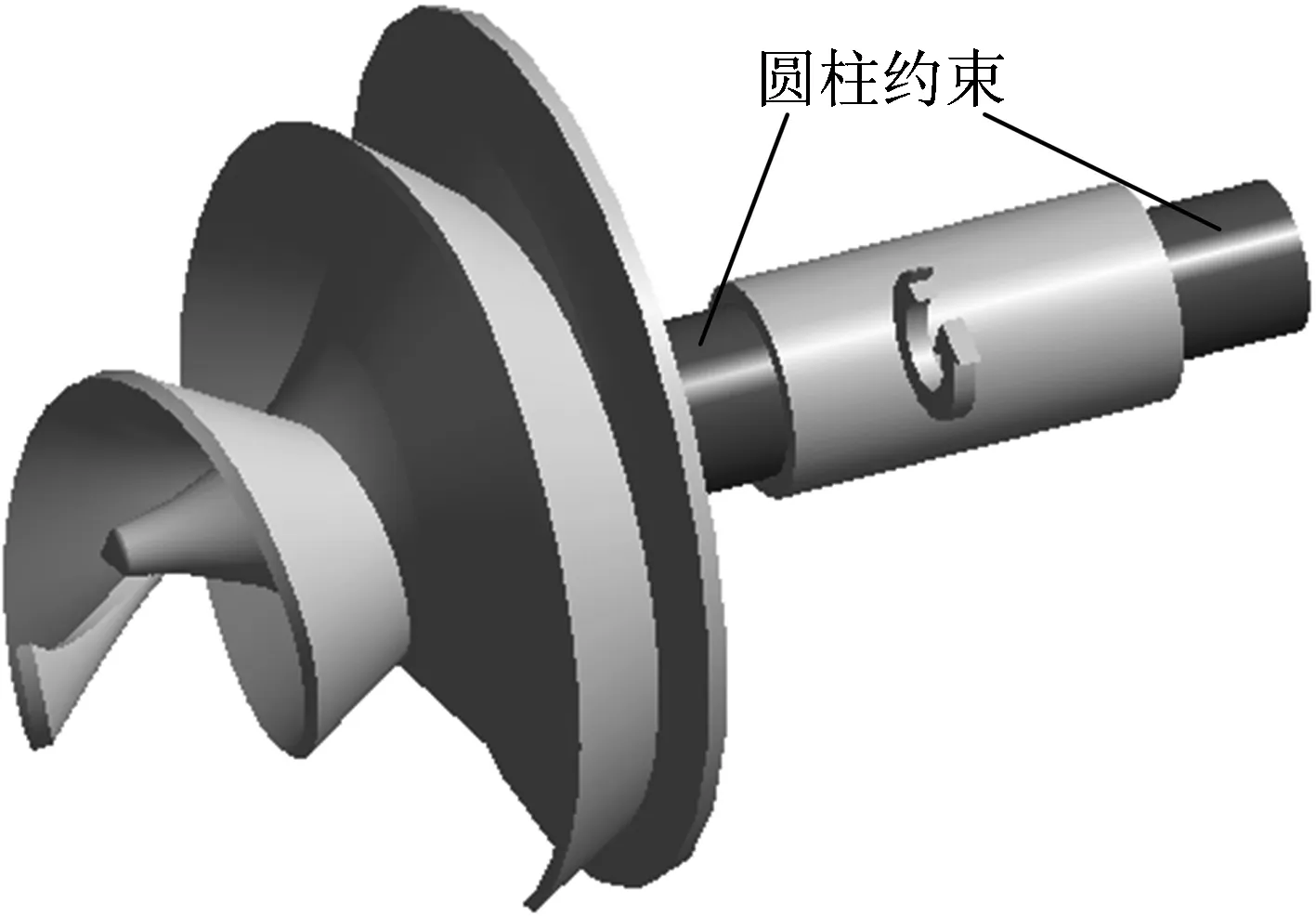
图3 转子部件约束

3 数值模拟结果与分析

3.1试验验证

为验证流固耦合计算和非流固耦合计算结果的可靠性，将两种数值模拟结果与清水试验结果进行对比，螺旋离心泵开式试验台如图4所示。分别提取螺旋离心泵在流固耦合计算和非流固耦合计算时的瞬时进出口压力和转矩，并将数据进行时均化处理，得出各工况下的扬程与效率的计算值，绘制出该模型泵的qV-H、qV-η曲线，并与开式试验台所做的外特性清水试验曲线相对比，结果如图5所示。泵扬程和效率的计算式如下：

(6)

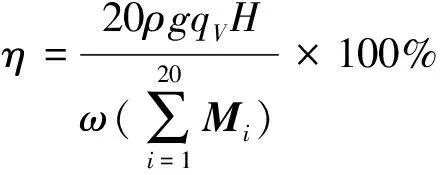
(7)

式中：H为泵的扬程；η为泵的效率；p2i和p1i分别为叶轮旋转到泵进出口的瞬时总压；ρ为液体密度；g为重力加速度；qV为液体体积流量；ω为叶轮旋转角速度；Mi为第i个数据提取点的转矩。

图4 螺旋离心泵试验台

从图5可以看出，2种数值计算模式得出的扬程和效率的预测曲线与清水试验所得曲线趋势基本一致，即2种数值计算模式的扬程和效率预测值在大流量工况和设计工况的计算值略低于试验值，而小流量时扬程和效率的预测值相对高于试验值。在设计工况附近，采用流固耦合计算时泵扬程的预测值与试验值误差不超过3%，但在0.4 qV和0.6 qV时扬程预测值与试验值出现较大偏差，分别为 8.5%和5.2%，在1.4 qV时扬程预测值与试验值偏差较小，为4%。而对于效率曲线，在小流量时预测值较试验值偏差较大，最大误差为7.9%，其他工况相对误差均在4%以内。

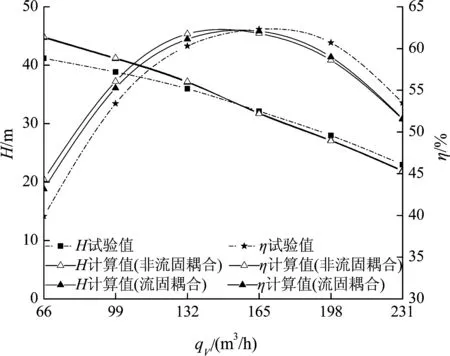
图5 泵性能的数值模拟曲线与试验曲线

同时，从图5可以看出，在设计工况和大流量下，采用流固耦合模式的预测扬程和效率较非流固耦合时有所升高,小流量时有所降低。总体而言，流固耦合计算的性能曲线相比非流固耦合计算更接近试验曲线，说明流固耦合计算对本研究中螺旋离心泵外特性的预测比非流固耦合计算更准确。

图6示出采用流固耦合和非流固耦合计算时扬程和效率在不同流量时的差值。可以看出，2种数值计算的扬程差值和效率差值随流量的增大而减小，说明流固耦合作用在小流量下对外特性的影响较大，在大流量下对外特性的影响较小。在小流量下扬程差值在0.14m以上，效率差值在0.8%以上；而在大流量下扬程差值在0.1m以下，效率差值在0.2%以下。这主要是由于相比大流量和设计工况，小流量时泵内压力更高，叶轮承受压力载荷更大。由于双向流固耦合计算模式考虑了流体对固体的作用及固体对流体的反作用，叶轮作为弹性体，受到流体载荷的作用必然导致叶片和轮毂发生变形，从而使流道几何边界发生改变，进而影响泵进出口相对速度的大小和方向，最终使两种计算模式下泵的扬程和效率曲线出现差异。

综上所述，2种计算模式的扬程和效率预测结果都较为准确地预测了该泵的外特性，也证实了采用这2种数值模拟方法能够反映出泵内液体流体的运动特征。采用流固耦合计算对扬程和效率的预测值较非流固耦合计算准确度更高，但采用流固耦合计算的工作量较大，计算周期较长；而2种数值计算模式对扬程和效率的预测结果差别较小，对于扬程和效率预测结果精度要求不是非常高时，采用非流固耦合即可满足要求。

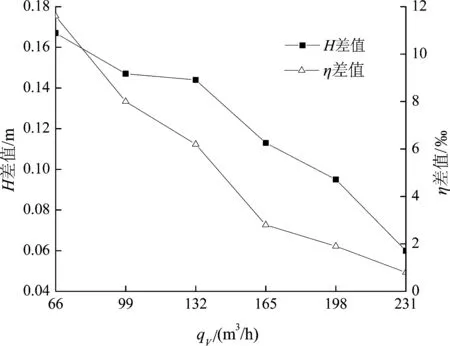
图6 扬程和效率在不同流量时的差值

3.2流固耦合作用对压力场的影响

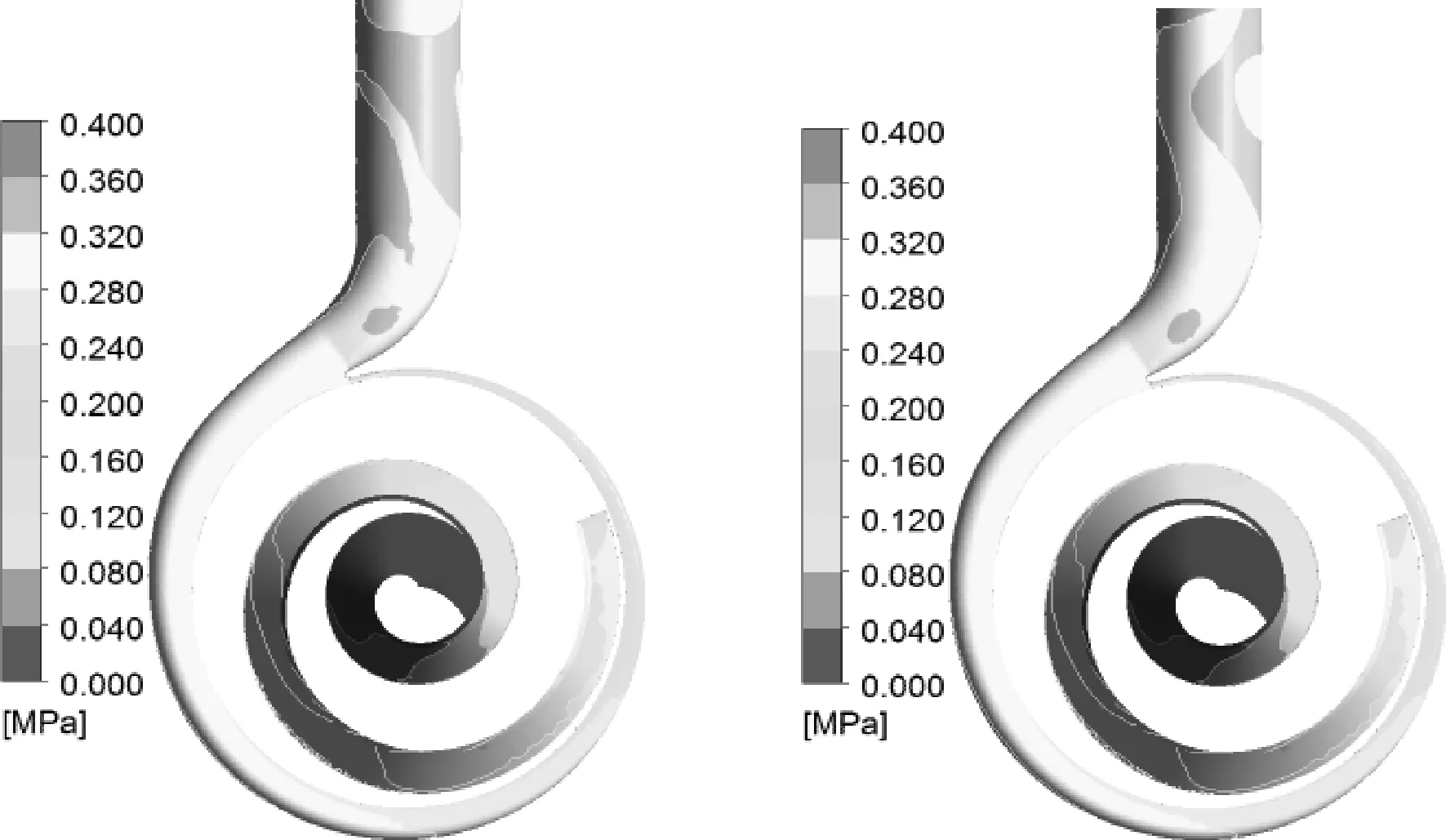
螺旋离心泵运行过程中，在复杂的水力激励作用下，其转子受到较大的周期性交变载荷影响，会引起叶片、轮毂及轴的变形，这必然会引起流场的变化。本研究对设计流量时不同时刻(叶轮相对蜗壳不同位置)流固耦合计算与非流固耦合计算的压力场进行对比，分析了流固耦合作用对螺旋离心泵压力场的影响。选取叶轮转过90°、180°、270°和360°时的叶轮工作面和蜗壳壁面流固耦合和非流固耦合计算时的压力云图，如图7所示。

从图7可以看出，对于2种数值计算模式，蜗壳和叶片工作面压力分布都出现较为明显的压力梯度，由于其叶轮是单叶片非对称性结构，导致叶片对液流的约束力有限，蜗壳与叶轮间的压差形成回流现象，叶片压力最大值出现在叶片出口前某处，而隔舌的作用使叶片出口附近的工作面上出现局部压力的最高点。

对比4种叶轮位置时流固耦合计算和非流固耦合计算的压力分布，可以看出：考虑流固耦合计算时蜗壳上的压力分布较非流固耦合计算时整体趋势基本一致；但在扩散段产生明显差异，而叶片上的压力分布几乎没有变化。这说明流固耦合作用在设计工况下对叶片压力分布影响较小，对蜗壳压力分布的影响主要集中在扩散段。扩散段上考虑流固耦合计算的均压明显高于非流固耦合计算时，也与2种数值计算模式所预测设计工况点的扬程关系一致。这是由于螺旋离心泵叶轮常采用大包角单叶片形式，且叶片相对较薄，叶轮在工作时承受分布不均、且随时间变化剧烈的压力载荷。而考虑流固耦合计算时，转子是弹性体，考虑了各种变形和阻尼振动，叶片和轮毂的变形使泵在运转时过流部件的形状与其流动情况不相适应，直接影响了泵内部的流动状态，对螺旋叶轮流场的扰动作用增强，进而影响到蜗壳内的流动。当叶轮转过90°和360°时，流固耦合作用使第八断面至喉部的高压区沿周向向喉部扩散，这是由于流固耦合作用使动静干涉作用增强所致。

叶轮转过90°

叶轮转过180°

叶轮转过270°

叶轮转过360°

(a) 流固耦合 (b) 非流固耦合

图7 不同叶轮位置的压力图

3.3流固耦合作用对速度场的影响

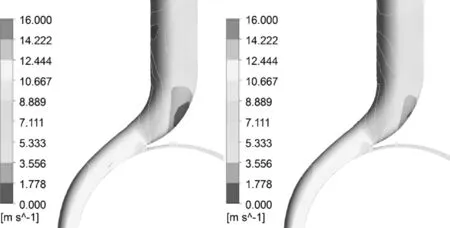
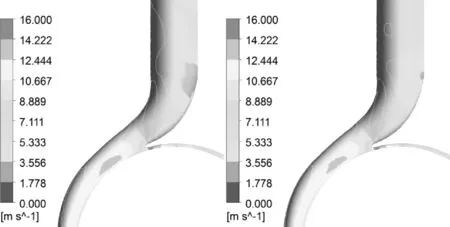
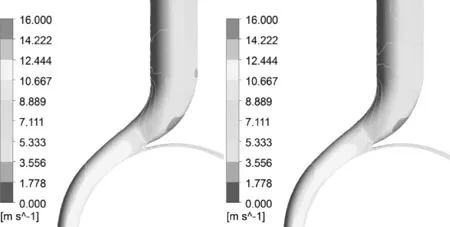
由于螺旋离心泵的流道变化和叶片扭曲较大，故其内部流动情况与一般离心泵差别较大[16]。为进一步研究流固耦合作用对其内部流场的影响，在设计工况下，基于第5周期的数据，选取叶轮转过90°、180°、270°、360°时流固耦合计算与非流固耦合计算的速度场进行对比研究。由于流固耦合作用对压力场的影响主要集中在扩散段，故作出扩散段速度云图对进行对比研究，如图8所示。

叶轮转过90°

叶轮转过180°

叶轮转过270°

叶轮转过360°

(a)流固耦合 (b)非流固耦合

图8 不同叶轮位置的速度图

从图8可以看出，对于不同叶轮位置，蜗壳的相对速度分布存在明显的速度梯度，从所截位置到蜗壳出口相对速度逐渐减小，符合速度分布的基本规律。流体经过隔舌时，流速呈不同程度的下降，并在扩散段产生一个低速区，且随着叶轮位置的不同其大小和位置都在变化，这是由于液流绕过隔舌时产生了漩涡和脱流所致。

对比4种叶轮位置时的图8(a)、(b)可知，同一叶轮位置上蜗壳扩散段内的相对速度分布有明显差别，扩散段采用流固耦合计算时的局部相对速度较非流固耦合计算时有所降低。这与扩散段总压的分布规律相反，符合蜗壳扩散段降速增压的基本规律。扩散段上的低速区在两种数值计算模式下也有所差别，在流固耦合作用下，低速区的范围不断扩大。这是由于转轴在转矩作用下发生扭转变形，导致叶轮结构与变形前相错一定角度，使叶片上的相对速度大小和方向发生改变，从而影响了蜗壳内的速度分布，使扩散段的相对速度在考虑流固耦合后局部变化明显；且叶轮出口变形导致叶轮出口液流角绝对速度发生变化，与隔舌角不匹配，导致扩散段内靠近隔舌处的漩涡和脱流加剧，使低速区在流固耦合作用下不断扩大。

3.4叶片扫过隔舌时流固耦合作用对压力场的影响

由于旋转叶轮与静止蜗壳隔舌间的动静耦合作用，是螺旋离心泵内部压力脉动的主要脉动源，且隔舌处的流动相对比较紊乱，叶片扫过隔舌时出口流量会发生改变。又由流固耦合作用对压力场和速度场的影响可知，流固耦合对蜗壳扩散段的影响较为明显，故提取设计工况下两种计算模式时叶片扫过隔舌的蜗壳扩散段中截面压力云图，即叶片扫过隔舌前(叶片出口相距隔舌18°)、叶片正对隔舌时(叶片出口正对隔舌)、叶片扫过隔舌后(叶片出口相距转过隔舌18°)，如图9所示。

从图9可以看出，在设计工况下叶片扫过隔舌时，采用两种计算模式的蜗壳扩散段总压分布均出现突变，平均总压明显低于扫过隔舌前后的平均总压。这是因为叶片扫过隔舌时，叶片转到隔舌位置时蜗壳的出口流量最大，出口压力最低。在流固耦合计算模式下蜗壳扩散段的平均总压高于非流固耦合计算时，这与设计工况下两种计算模式的扬程关系相符合，造成总压差异主要是由于流固耦合作用使叶片产生变形，导致叶片出口位置发生改变，使叶轮出口绝对速度的大小和方向都发生变化。而在叶片扫过隔舌前后，隔舌至第1断面的压力分布在流固耦合作用下明显降低。这是由于叶片的变形导致隔舌处回流的增加，从而出现压力降低的现象。

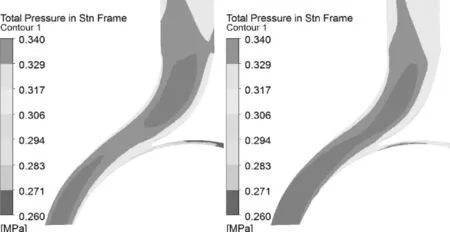
叶片扫过隔舌前

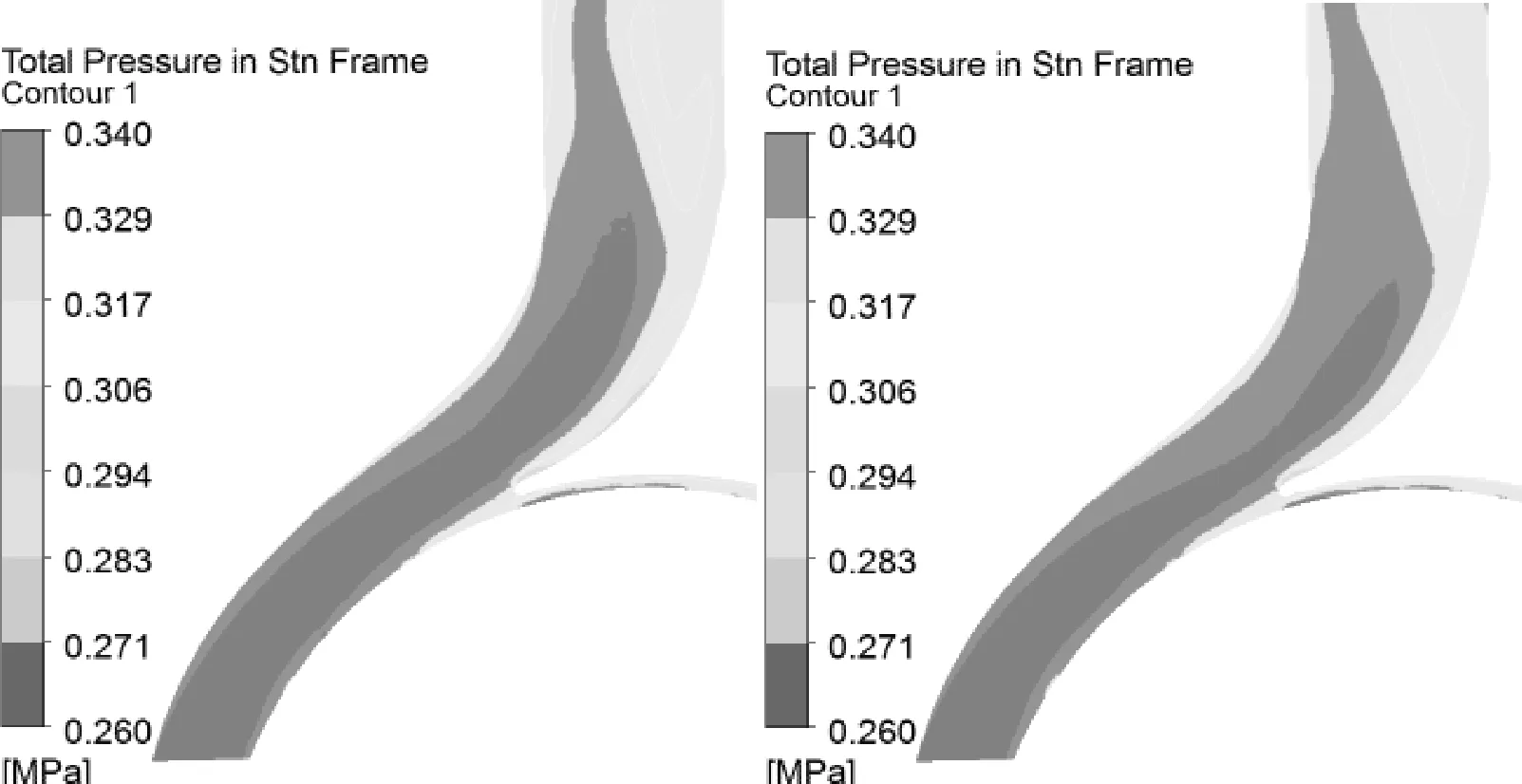
叶片正对隔舌时

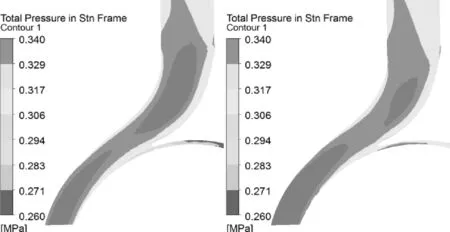
叶片扫过隔舌后

(a)流固耦合 (b) 非流固耦合

图9 蜗壳扩散段中截面的总压图

4 结论

1)流固耦合计算得到的扬程和效率预测值相比非流固耦合计算更精确，在小流量下流固耦合作用对扬程和效率的预测结果影响较大,在大流量下对扬程和效率的预测结果影响较小。

2)流固耦合作用使蜗壳扩散段压力分布产生明显变化，但对蜗壳其他部位和叶片工作面压力分布影响不大，且当叶轮转过90°和360°时，流固耦合作用使第八断面至喉部的高压区沿周向向喉部扩散。

3)流固耦合作用使蜗壳扩散段的相对速度产生明显差别，考虑流固耦合时局部的相对速度低于非流固耦合时，扩散段在流体绕过隔舌后产生一个低速区并使扩散段的低速区范围不断扩大。

4) 在设计工况下，采用2种计算模式的蜗壳中截面总压分布产生明显差别，且在叶片出口正对隔舌时总压分布均出现突变。

[1]李仁年,李兵,韩伟. 螺旋离心泵工作特性理论分析 [J]. 农业机械学报,2005, 36(6):51-53.

[2]王秋红. 螺旋离心泵内固液两相流的CFD数值模拟 [D].兰州:兰州理工大学,2005.

[3]刘宜，赵希枫，惠伟安，等.螺旋式离心泵性能的试验与分析[J].西华大学学报:自然科学版,2008，27(3)：3-5.

[4]徐宇平,袁寿其,张金凤,等. 螺旋离心泵研究现状及前景[J]. 流体机械,2012,40(4):35-40.

[5]程效锐,李仁年,黎义斌,等. 螺旋离心泵瞬态特性的数值分析 [J].机械工程学报,2013,49(8):186-192.

[6]李仁年,李兵,韩伟. 螺旋离心泵工作特性理论分析 [J]. 农业机械学报, 2005, 36(6):51-53.

[7]曾娜,郭小刚. 探讨流固耦合分析方法 [J]. 水科学与工程技术,2008(增刊):65-68.

[8]PEI Ji, YUAN Shouqi, YUAN Jianping, et al. Numerical calculation for effect of fluid and structure interaction on flow field in centrifugal pump[J].Transactions of the Chinese Society for Agricultural Machinery,2009, 40(12):107-112.

[9]YUAN Shouqi, PEI Ji, YUAN Jianping, et al. Numerical investigation on fluid structure interaction considering rotor deformation for a centrifugal pump[J].Chinese Journal of Mechanical Engineering, 2011,24(4) :539-545.

[10]钱若军,董石麟,袁行飞. 流固耦合理论研究进展 [J]. 空间结构,2006,14(1):3-14.

[11]江伟,郭涛,李国君,等. 离心泵流场流固耦合数值模拟 [J]. 农业机械学报,2012,43(9):53-56.

[12]王洋,王洪玉,张翔. 基于流固耦合作用的离心泵冲压焊接叶轮强度分析 [J]. 排灌工程机械学报,2011,29(2): 109-113.

[13]袁寿其,徐宇平,张金凤,等. 螺旋离心泵转子系统动态响应数值分析 [J]. 农业机械学报,2013,32(6):163-167.

[14]李仁年,王秋红,刘成胜. 求解螺旋离心泵内部流动的数值模型 [J]. 兰州理工大学学报,2006,32(1):57-60.

[15]PEI Ji, BENRA F-K. Application of different strategies of partitioned fluid-structure interaction simulation for a single-blade pump impeller[J]. Journal of Mechanical Engineeriing,2012,226(4):297-308.

[16]丁思云，杨博峰，郑国运,等.叶片数对螺旋离心泵内部流场影响研究 [J]．流体机械,2009,37(7):33-37.

(编校：夏书林)

BidirectionalFluidStructureInteractionAnalysisfortheScrewCentrifugalPump

LIU Yi1,2, BAI Mao-ning, CHENG Xiao-rui1,2, JIA Cheng-li1

(1.SchoolofEnergyandPowerEngineering,LanzhouUniversityofTechnology,Lanzhou730050China；2.KeyLaboratoryofFluidMachineryandSystems,GansuProvince，Lanzhou730050China)

A full three-dimension bidirectional fluid-structure coupled simulation combined the inner flow field and structure field is established to study the effect of FSI on external characteristics and the pressure field and velocity field at different positions of the impeller in screw centrifugal pump with single blade. For the calculation, the flow field is based on Reynolds-averaging N-S equations and standard two equation k-ε turbulent model with multiple reference frame, and the structure response is based on elastic structural dynamic equation. Compared the results with FSI to that without FSI, the analysis shows that the head and efficiency curve with FSI are much closer to test values, the effect of FSI on external characteristics under low flow rate is larger than that under high flow rate. The effect of FSI on the pressure field and velocity field mainly concentrate in diffuser and less effect on blade and other part of volute. The pressure distribution occurs a significant difference with two calculation methods at the volute middle section，and the pressure distribution produces mutation when the outlet of impeller directly face cutwater.

screw centrifugal pump； sidirectional fluid structure interaction； numerical calculation； flow fields； external characteristic

2014-11-12

甘肃省自然科学基金(2011GS04252)。

刘宜(1955—)，男，教授级高工，主要研究方向为流体机械。

TH311

：A

：1673-159X(2015)06-0085-07

10.3969/j.issn.1673-159X.2015.06.018