基于前景理论的直觉模糊决策方法及其在配送中心选址中的应用
李 梅1,2,吴 冲1,张 雷
(1.哈尔滨工业大学管理学院,黑龙江 哈尔滨 150001;2.广西师范学院物流管理与工程学院,广西 南宁 530001;3.浙江财经大学工商管理学院,浙江 杭州 310018)
·新能源汽车与低碳运输·
基于前景理论的直觉模糊决策方法及其在配送中心选址中的应用
李 梅1,2,吴 冲1,张 雷3
(1.哈尔滨工业大学管理学院,黑龙江 哈尔滨 150001;2.广西师范学院物流管理与工程学院,广西 南宁 530001;3.浙江财经大学工商管理学院,浙江 杭州 310018)
为提高配送中心选址的效率,构建基于前景理论的直觉模糊多属性决策方法,并将其应用于配送中心的选址决策中。介绍直觉模糊集的相关概念,提出一种改进的得分函数算法,并与前景理论相结合构建新的决策模型。在此基础上对配送中心选择的决策流程进行规划,并选取营运成本、交通因素、客户服务等指标构建配送中心选址的评价指标体系。通过算例对某电商平台的配送中心选址决策进行评价。本方法一方面在决策评价过程引入直觉模糊数,充分考虑决策过程中专家评价的不确定性和专家打分的犹豫度水平;另一方面使用基于前景理论的决策方法进行综合评价,充分考虑人们在面临收益和损失时风险偏好的差异性,使得决策结果更加符合人们的真实意图,从而得到更合理的决策效果。算例结果表明,本文方法与直觉模糊TOPSIS决策方法的计算结果一致,且前者的区分度更大,更有利于配送中心水平的划分,进而提高决策的质量,降低决策风险。
前景理论;直觉模糊集;得分函数;熵;配送中心选址
随着物流专业化水平的不断提升,配送中心在供应链中的作用也日渐重要。这种重要性主要体现在2个方面:一方面,合适的配送中心的选址和布局规划能够提高供应链的运营效率;另一方面,配送中心高水平的管理能力、先进的技术设备和信息化程度等软实力能促进整个供应链的协调发展。本文重点研究前者。配送中心选址在整个供应链建设过程中处于核心地位,要综合考虑供应链中的供应商、生产商、分销商乃至客户等众多物流节点的利益,可以说配送中心选址是一项系统工程。
目前,学者们对配送中心选址的模型和方法进行了一些研究,主要集中于层次分析法(AHP)及其派生方法[1-2]、蚁群算法[3]、遗传算法[4]以及运筹学综合优化算法[5-6]等,并将其应用于冷链配送中心选址、农产品物流配送中心选址和城市交通枢纽选址等领域,取得了不少应用性的成果。本文借鉴并改进已有的研究成果,构建配送中心选址的评价指标体系,并采用基于前景理论的直觉模糊多属性决策方法对选址决策进行分析,为此类问题提供一种新的算法。本文的创新之处在于:一方面,决策评价过程引入直觉模糊数,充分考虑了决策过程中专家评价的不确定性和专家打分的犹豫度水平,使属性评价值合理性增强,更加符合实际工作需求,同时构建了新的直觉模糊得分函数,避免决策信息的丢失;另一方面,使用基于前景理论的决策方法[7]进行综合评价。该方法是一种基于决策者行为心理的决策方法,它以“有限理性人”为基本假设,充分考虑了人们在面临收益和损失时风险偏好的差异性,并以“价值函数”和“权重函数”代替传统期望效用理论中的“效用函数”和“概率函数”,使得决策结果更加符合人们的真实意图,从而得到更合理的决策效果。
1 直觉模糊集及前景理论
1.1直觉模糊集及直觉模糊数运算规则
直觉模糊集是Atanassov[8-9]对Zadeh[10]传统模糊集理论的扩展,可以更好地处理模糊信息,将直觉模糊集运用到多属性决策问题中是十分有效的,能够更加细腻地刻画信息模糊性的本质,使得评价不确定信息时具有更强的表现能力。
定义1[8]设X是一个非空集合,则论域X上的直觉模糊集A可表示为

(1)
式中,μA(x)和νA(x)分别为X元素中x属于A的隶属度和非隶属度,即μA:X→[0,1],x∈X→μA(x)∈[0,1],νA:X→[0,1],x∈X→νA(x)∈[0,1]。同时,满足0≤μA(x)+νA(x)≤1;犹豫度或不确定度记为πA=1-μA(x)-νA(x)。显然,对于任意的x∈X,都有0≤πA(x)≤1。
直觉模糊数的一些基本运算法则如定义2所示。
定义2[11]若α=(μα,να),α1=(μα1,να1)和α2=(μα2,να2)均为直觉模糊数,则:
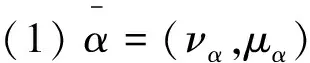
(2)α1∧α2={min(μα1,μα2),max(να1,να2)};
(3)α1∨α2={max(μα1,μα2),min(να1,να2)};
(4)α1⊕α2=(μα1+μα2-μα1μα2,να1να2);
(5)α1⊗α2=(μα1μα2,να1+να2-να1να2);
(6)λα=(1-(1-μα)λ,ναλ),λ>0;
(7)αλ=(μαλ,1-(1-να)λ),λ>0。
1.2一种新的直觉模糊得分函数
任意给定一个直觉模糊数α=(μα,να),可以通过得分函数来对其进行评估[12]:
s(α)=μα-να。
(2)
式中s(α)为α的得分值,显然,s(α)∈[-1,1]。
由式(2)可知,直觉模糊数α的得分值与其隶属度μα和非隶属度να的差值直接相关,即μα和να的差值越大,α的得分值越大,从而直觉模糊数α也越大;但是在某些特殊的情况下,无法通过得分函数来比较直觉模糊数的大小。如对于直觉模糊数α1=(0.8,0.1)和α2=(0.7,0.0),由式(2)可得,s(α1)=s(α2)=0.7,无法判断α1和α2的大小。
为了克服这种不足,Hong等[13]给出了另一种刻画直觉模糊数的函数,称之为精确函数:
h(α)=μα+να。
(3)
式中h(α)为α的精确度。
h(α)值越大,表示直觉模糊数α的精确度越高。根据式(3),在上例中,h(α1)=0.9,h(α2)=0.7,显然,h(α1)>h(α2),也就是说直觉模糊数α1的精确度要高于直觉模糊数α2。
定义3[14]设α1=(μα1,να1)和α2=(μα2,να2)为直觉模糊数,s(α1)和s(α2)分别是α1和α2的得分值,h(α1)和h(α2)分别是α1和α2的精确度,那么:
(1)若s(α1) (2)若s(α1)=s(α2),则当h(α1) 然而,在直觉模糊数比较大小时,不难发现上述得分函数和精确函数的局限性,如对于上例的直觉模糊数α1=(0.8,0.1)和α2=(0.7,0.0),根据公式判断α1>α2。这显然与大多数风险厌恶型(从理性学说来看,大多数的决策者都是风险厌恶者)的决策人的直觉判断相悖,用以上的得分函数和精确函数进行决策势必会带来决策结果的偏误。基于这一情况,本文提出以下的修正得分函数: (4) 该公式同时考虑了直觉模糊数的隶属度、非隶属度和犹豫度3个部分,分别为μα、να和πα。在直觉模糊数的概念中,隶属度往往代表决策者对方案的赞成程度,非隶属度代表决策者对方案的反对程度,而犹豫度代表决策者对方案的不确定程度。在新构建的直觉模糊得分函数sL(α)中,我们认为,决策者支持的比例μα越高越好,而反对的比例να越小越好。假设当μα确定的时候,1-μα=να+πα即为固定的值;所以当να越大时,相对不确定程度πα的值就越小,从而得分函数值不确定的可能性就越小,得分函数sL(α)的值就越大。 定理1 (单调性)得分函数sL(α)关于隶属度μα是单调递增的,关于非隶属度να是单调递减的。 由此可见,sL(α)关于μα是单调递增的,关于να是单调递减的。 定理2 (有界性)得分函数sL(α)是有界的,且sL(α)∈[-1,1]。 定理3 (比较规则)假设α1=(μα1,να1)和α2=(μα2,να2)为2个直觉模糊数:若sL(α1)>sL(α2),则α1>α2,反之亦然;若sL(α1)=sL(α2),则α1~α2。 从以上的定理可以看出,新构建的得分函数sL(α)有以下优势: 1)和文献[12-14]的得分函数相比,直觉模糊数排序不需要两个函数,只要一个函数即可; 2)具有单调性、有界性等优良性质,强调μα对得分函数的促进作用和να对函数的阻碍作用,同时充分考虑了犹豫度πα对整个得分函数的影响。 3)具有较强的比较能力,对于前文所列举的直觉模糊数α1=(0.8,0.1)和α2=(0.7,0.0),通过新构建的得分函数sL(α)计算可得:sL(α1)=0.691,sL(α2)=0.700,显然,sL(α1) 1.3前景理论 Kahneman等[7]提出的前景理论修正了传统决策的期望效用理论,并构建了一种新的决策框架模型。它假设风险决策过程分为编辑和评价2个阶段。在编辑阶段,个体凭借框架(frame)、参照点(reference point)等采集和处理信息,在评价阶段依赖价值函数(value function)和主观概率的权重函数(weighting function)对信息予以判断,并解释了人们对待收益和损失的时候价值函数的“S形”变化。由于提出了期望价值理论,为风险决策领域带来巨大贡献,Kahneman获得了2002年的诺贝尔经济学奖。 在前景理论中,前景价值是由价值函数和权重函数共同决定的,即 V=∑v(x)π(p)。 (5) 式中,v(x)表示价值函数,是决策者根据实际的收益或损失所产生的主观感受的价值,π(p)是决策权重函数。 (6) 式中:当x≥0时,表示获得收益;当x<0时,表示蒙受损失。α和β分别表示价值函数在收益和损失区域的凹凸程度,即反映了决策者对收益和损失的敏感性程度。权重函数的表达形式为 (7) 式中:p为概率;ξ和τ表示权重函数的变化程度,也反映了决策者对待收益和风险的不同态度[7]。在前景理论的价值函数和权重函数中,共有α、β、ϑ、ξ和τ5个参数,Tversky和Kahneman通过大量的实验数据分析得出α=β=0.88,ϑ=2.25,ξ=0.61,τ=0.69。 1.4熵权法确定属性权重值 熵的概念首先由德国物理学家Rudolf Clausius提出,本来是热力学中的概念,用来对混乱和无序的程度进行度量。熵值越大,混乱无序的程度越大。Burillo等[15]最先给出了一个直觉模糊熵的定义,在此基础上又有学者给出了不同形式的直觉模糊熵的计算方法[16]。 熵权法中,关键是如何求得属性值的熵。假设一个离散信源可以表示为 (8) (9) 式中,k=1,通常选取e做为对数函数的底。下面将熵理论推广到直觉模糊领域。 在具体的决策问题中,针对每一个备选方案Ai(i=1,2,…,m)在属性Cj(j=1,2,…,n)的条件下形成直觉模糊决策矩阵D=(dij)m×n,dij=(μij,νij)。首先,求解方案Ai关于属性Cj的特征信息的得分函数值,然后做归一化处理,使得 (10) 进而利用式(11)求各属性Cj的平均信息熵。 (11) 接着计算各属性的综合权重: (12) 2.1问题描述 2.2决策步骤 步骤1 获取决策者的决策信息,包括各种方案集、属性集和用直觉模糊数表达的决策属性值等相关信息,并将直觉模糊决策矩阵转化为得分函数矩阵; 步骤2 利用前景理论的相关公式计算备选方案的前景价值; 步骤3 通过直觉模糊熵的相关信息计算各准则的权重; 步骤4 综合计算各备选方案的综合前景价值,并进行排序比较和结果分析。 配送中心是供应链的核心节点,其选址在配送中心建设过程中处于基础性的重要地位。一般来说,传统配送中心选址主要考虑运营成本、交通因素及辐射能力等基础指标。不同类型的配送中心在选址时又有不同的具体要求,如冷链配送中心要求其具备相应的冷链基础条件,农产品配送中心要靠近货源采集地等。总之,全面客观考虑配送中心的选址指标和因素,能够方便上下游企业更好地沟通合作、降低运营成本、提升物流专业化水平进而提升整个供应链的效率。 通过归纳梳理大量文献,结合配送中心选址的实际情况,并综合专家意见,最终确立了配送中心选址的10项指标,并将其整合为4项指标(C1~C4)。由于指标数量较多,为了便于专家快速、准确、全面打分,本文设计了配送中心选址的指标因素,如图1所示。 图1 配送中心选址指标因素 某大型电子商务平台拟对新建配送中心进行选址,备选方案有3个,分别位于城东A1、城西A2和城北A3,由于该电子商务平台属于综合型的零售业态,故在考虑选址指标时,综合考虑C1~C4等4个因素,如图1所示。由于指标权重未知,决策专家在选址时充分考虑了评价属性值的不确定性和风险性,故采用直觉模糊数来进行评价。 下面采用基于前景理论的直觉模糊多属性方法对该选址进行决策。 步骤1 获取决策者的决策信息,包括各种方案集、属性集和用直觉模糊数表达的决策属性值等相关信息,并将直觉模糊决策矩阵转化为得分函数矩阵。 物流中心选址的初始决策矩阵如下: C1C2C3C4 A1(0.5,0.3) (0.6,0.3) (0.5,0.2) (0.7,0.1) A2(0.4,0.3) (0.7,0.2) (0.5,0.3) (0.6,0.3) A3(0.8,0.1) (0.2,0.4) (0.3,0.6) (0.4,0.5) 将以上直觉模糊决策矩阵转化为得分函数矩阵为 步骤2 利用前景理论的相关公式计算备选方案的前景价值: 步骤3 通过直觉模糊熵的相关信息计算每个准则的权重,得到: ω1=0.452;ω2=0.136;ω3=0.213;ω4=0.198。 步骤4 综合计算各备选方案的综合前景价值,并进行排序比较和结果分析,得到: v1=0.317;v2=0.236;v3=0.703。 按综合前景值的大小给3个配送中心选址进行排序,A1>A2>A3,因此位于城东的A1为该电商选择配送中心的最优选址。 利用文献[17]的直觉模糊TOPSIS决策方法对本文算例进行求解,3个配送中心贴进度水平ρ计算如下:ρ1=0.633,ρ2=0.388,ρ3=0.354,3个配送中心选址的排序仍为A1>A2>A3,和本文方法计算结果一致,证明了本文方法的有效性。另外,本文的计算结果比文献[17]计算结果的区分度更大,更有利于配送中心水平的划分,进而提高决策的质量,降低决策风险。 本文构建了基于前景理论的直觉模糊多属性决策方法,并将其应用于配送中心的选址决策问题。一方面,决策评价过程引入直觉模糊数,充分考虑了决策过程中专家评价的不确定性和专家打分的犹豫度水平,使属性评价值合理性增强,更加符合实际工作需求,同时,构建了新的直觉模糊得分函数,避免决策信息的丢失;另一方面,使用基于前景理论的决策方法进行综合评价,充分考虑了人们在面临收益和损失时的风险偏好的差异性,使得决策结果更加符合人们的真实意图,从而得到更合理的决策效果。通过算例分析可知,本方法具有一定的优越性,同时也为配送中心选址提供了一种新的算法。 [1]莫海熙, 郜振华, 陈森发.基于AHP和目标规划的物流配送中心选址模型[J].公路交通科技, 2007, 24(5):150-153. [2]郭轶,周丹.基于TOPSIS/DEA/AHP法的物流配送中心选址问题分析[J].重庆工学院学报:自然科学版, 2009, 23(11):76-80. [3]秦固.基于蚁群优化的多物流配送中心选址算法[J].系统工程理论与实践, 2006(4):120-124. [4]周兴龙,金鹏飞.基于遗传算法的单点物流选址问题探析[J].物流工程与管理, 2010, 32(7):39-42. [5]项勇,卢永琴,李海凌.城市商品砂浆配送中心选址研究[J].西华大学学报:自然科学版, 2008, 27(4):93-96. [6]雷磊.综合运输枢纽公路客运场站布局方法研究[J].西华大学学报:自然科学版, 2006, 25(6):26-28. [7]Tversky A, Kahneman D. Advances in prospect theory: Cumulative representation of uncertainty[J].Journal of Risk and Uncertainty, 1992, 5(4):297-323. [8]Atanassov K. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems,1992, 20(1): 87-96. [9]Atanassov K. More on intuitionistic fuzzy sets[J].Fuzzy Sets and Systems, 1989, 33(1):37-45. [10]Zadeh L A. Fuzzy sets[J].Information Control, 1965, 8(3): 338-353. [11]Atanassov K. New operations defined over the intuitionistic fuzzy sets[J].Fuzzy Sets and Systems, 1994, 61(2): 137-142. [12]Chen S M,Tan J M.Handling multi:criteria fuzzy decision making problems based on vague set theory[J].Fuzzy Sets and Systems, 1994, 67(2):163-172. [13] Hong D H, Choi C H. Multicriteria fuzzydecision-making problems based on vague set theory[J]. Fuzzy Sets and Systems, 2000, 114(1):103-113. [14]Xu Z S. Some geometric aggregation opertators based on intuitionistic fuzzy sets[J].International Journal of Grneral Systems, 2006, 35(2):417-433. [15]Burillo P, Bustince H. Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets[J].Fuzzy Sets and Systems, 1996, 78(3):305-316. [16] Szmidt E, Kaeprzyk J. Entropy for intuitionistic fuzzy sets[J].Fuzzy Sets and Systems, 2011, 118(3):467-477. [17]南江霞, 李登峰, 张茂军.直觉模糊多属性决策的TOPSIS法[J].运筹与管理, 2008, 17(3):34-37. (编校:夏书林) IntuitionisticFuzzyDecisionMakingMethodbasedonProspectTheoryandItsApplicationinDistributionCenterLocation LI Mei1,2,WU Chong1, ZHANG Lei3 (1.SchoolofManagement,HarbinInstituteofTechnology,Harbin150001China;2.SchoolofLogisticsManagementandEngineering,GuangxiTeachersEducationUniversity,Nanning530001China;3.CollegeofBusinessAdministration,ZhejiangUniversityofFinanceandEconomics,Hangzhou310018China) In this paper, we construct an intuitionistic fuzzy multiple attribute decision making method based on prospect theory in order to improve the location efficiency of the distribution center, and apply it to the location decision of distribution center. Firstly, this paper introduces the related concepts of intuitionistic fuzzy sets; secondly, proposes an improved scoring function algorithm and builds a new decision-making model with the prospect theory, based on which the decision process of the distribution center selection is planned, and then the evaluation indicator system is built selecting the operating cost, the traffic factor and the customer service as the evaluation indicators; finally, the decision about the distribution center location of some electric business platform is evaluated by a numerical example. This method on the one hand introduces the intuitionistic fuzzy number in the decision evaluation, and takes into account the uncertainty of expert evaluation and the degree of uncertainty. On the other hand, making a comprehensive evaluation with the method of decision-making based on prospect theory, has fully considered the difference of the risk preference in the face of the income and the loss, so that the decision result is more consistent with people's true intention and we can get more reasonable decision effect from it. The calculation result shows the results of this paper are consistent with the results of the original intuitionistic fuzzy TOPSIS decision method, and the former is more differentiated, thus more advantageous to the distribution of the center level, and then we can finally improve the quality of decision-making and reduce the risk of decision-making. prospect theory; intuitionistic fuzzy sets; score function; entropy; distribution center location 2015-08-20 国家自然科学基金项目(71271070);高等学校专业综合改革试点项目(ZG0429)。 李梅(1981—),女,副教授,在读博士,主要研究方向为物流与供应链管理。 C934 :A :1673-159X(2015)06-0001-05 10.3969/j.issn.1673-159X.2015.06.001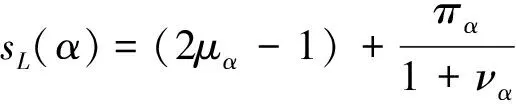
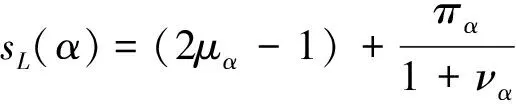
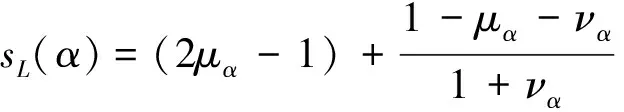
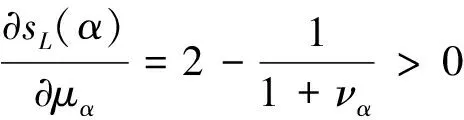
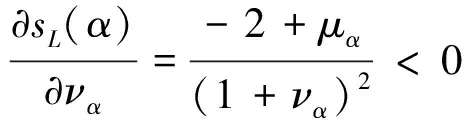
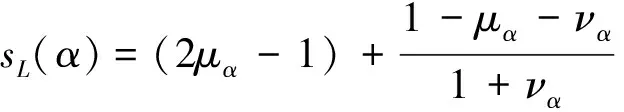
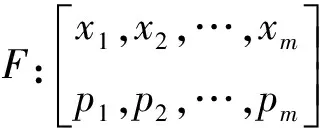
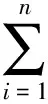
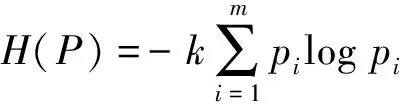
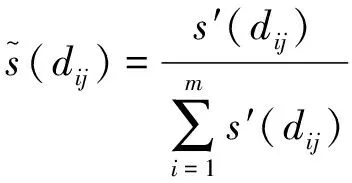
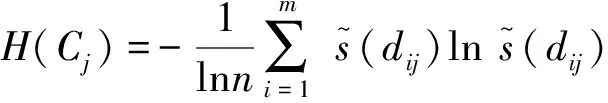

2 基于前景理论的直觉模糊多属性决策方法
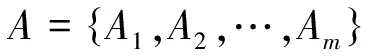
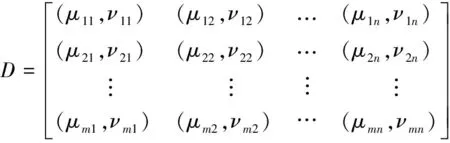
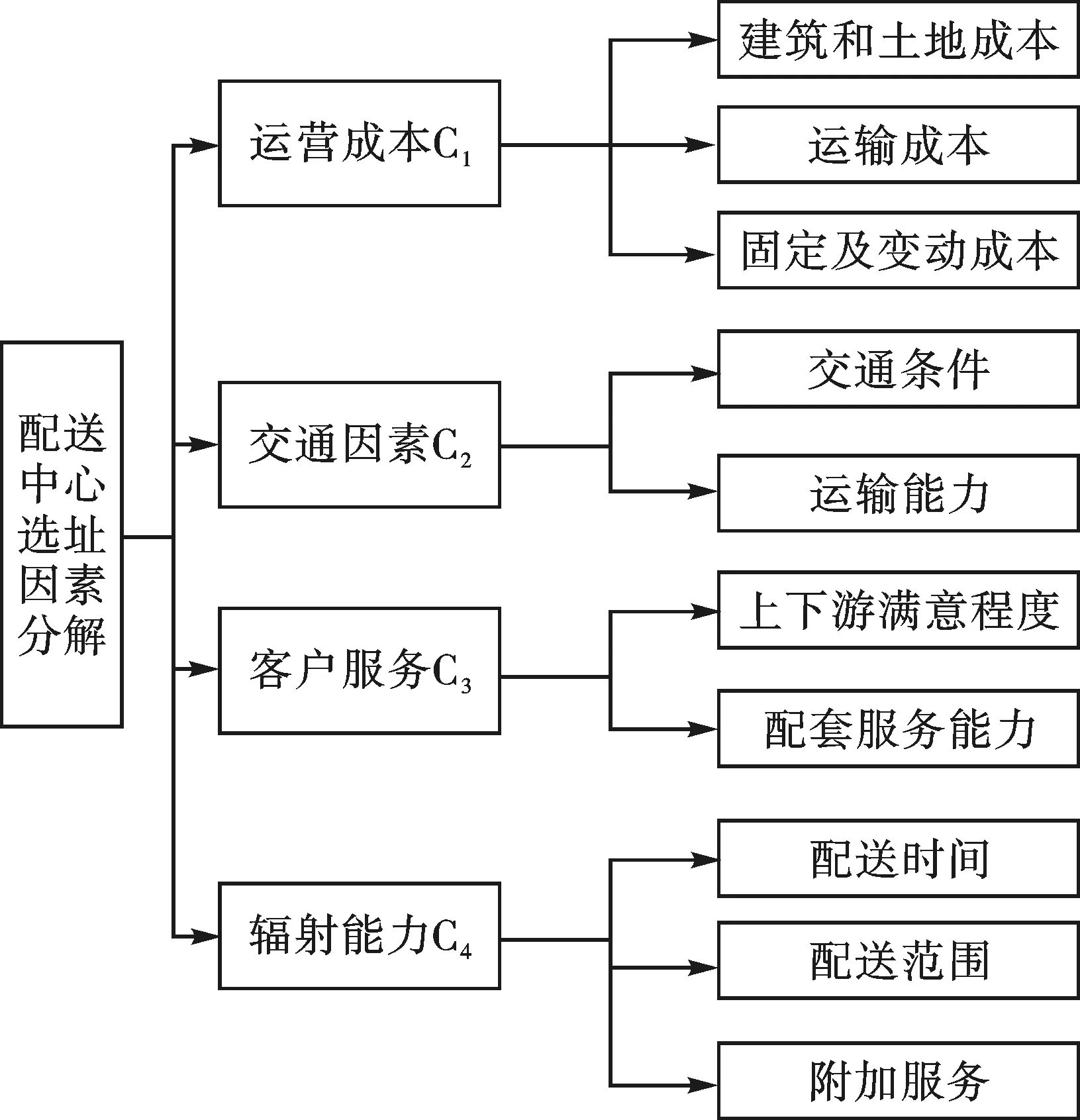
3 配送中心选址指标体系构建
4 算例分析


5 结论

