风波流联合作用下的浅海域隔水导管屈曲仿真

郑运虎,姜 峰

(兰州理工大学石油化工学院 ， 甘肃 兰州 730050 )

· 能源与环境·

风波流联合作用下的浅海域隔水导管屈曲仿真

郑运虎,姜 峰*

(兰州理工大学石油化工学院 ， 甘肃 兰州 730050 )

在对隔水导管进行受力分析的基础上，拟合出风、波、流载荷随高度和深度变化的函数关系式。以某浅海油田工程为例，联合风、波、流的共同作用力，采用Workbench模拟导隔水管在最恶劣工况下屈曲响应和应力分布，得出隔水导管的临界失稳载荷与形变特点以及应力分布，指出结构薄弱环节；根据所得固有频率，算得各阶频率所对应的共振转速。

隔水导管；屈曲分析；临界载荷；固有频率；五阶波

屈曲分析主要用于研究结构在一定载荷下的稳定性，最终是为了确定结构的临界失稳载荷值和屈曲形态。屈曲分析包括线性屈曲和非线性屈曲。线性(特征值)屈曲的计算结果偏保守(偏安全)，不完全用于实际工程问题分析；但是实际结构常常会因自身的缺陷和非线性载荷在结构尚未达到理论屈曲载荷时就已失稳。线性屈曲计算速度快，计算结果较保守，所以可用线性屈曲分析来预算结构屈曲临界载荷与形变大小。

海洋石油隔水导管的主要功能是隔离海水，形成钻井液循环的通道。其结构简单，但工作环境和受力状况极其复杂，在海上作业时导管不仅要受到井口的持久压载，同时还要受到风、浪、流、自重以及钻头转速等因素的影响，这些载荷对隔水导管的安全作业构成了严重威胁；因此对隔水导管进行屈曲分析，预测结构的失稳载荷和屈曲形态有重大意义。隔水导管通常以打桩的形式被打入海底，顶端受持久压载，底端嵌入海底岩土中，所以工程计算时通常将隔水导管简化为顶端铰支和底端固支的约束方式，来对隔水导管进行失稳分析和强度计算。本文采用stokes五阶波理论计算波浪力，与线性波和三阶波理论相比,计算结果能更真实地反映波浪载荷。所施加的波浪力、风力和海流力均为变载荷，与其他计算方式相比能更真实模拟受力状况。隔水导管受力情况如图1所示。

图1 隔水导管受力示意图

1 隔水导管受力分析

1.1波浪载荷

当结构物的尺度为D/L≤0.2时，为小尺度物(D为导管直径，L为波长)，可采用Morison公式进行波浪力计算，其方程[1-5]如下：

(1)

c[(λA11+λ3A13+λ5A15)chk(z+d)cosθ+

2(λ2A22+λ4A24)ch2k(z+d)cos2θ+

3(λ3A33+λ5A35)ch3k(z+d)cos3θ+

4λ4A44ch4k(z+d)cos4θ+

5λ5A55ch5k(z+d)cos5θ]；

(2)

ωc[(λA11+λ3A13+λ5A15)chk(z+d)sinθ+

22(λ2A22+λ4A24)ch2k(z+d)sin2θ+

33(λ3A33+λ5A35)ch3k(z+d)sin3θ+

44λ4A44ch4k(z+d)sin4θ+

55λ5A55ch5k(z+d)sin5θ]；

(3)

L=(gT2/2π)tanh(kd)；

(4)

k=2π/L。

(5)

Stokes五阶波波面方程

λcosθ+(λ2B22+λ4B44)cos2θ+

(λ3B33+λ5B35)cos3θ+λ4B44cos4θ+

λ5B55cos5θ。

(6)

将坐标轴选建在海底平面上，代入所查取的量纲一参数便可计算出相应结果。式中：Fw为柱体单位长度上的水平波浪力，N/m；CM为惯性力系数，壳牌公司取值为1.5～2；CD为阻力系数，壳牌公司取值为0.5～1.2；ux为水平方向的海水速度，m/s；ax为水平方向的海水加速度，m/s2；L为波长，m；k为波数；D为管柱直径；d为水深，m；T为周期，s；g为重力加速度，取值为9.81 m/s2；η为波面高度函数，m；ρw为海水密度，1 025 kg/m3；λ、A11、A13、A15、A22,、A24、A33、A35、A44、A55、B22、B24、B33、B35、B44、B55均为量纲—参数，可通过d/L的比值在文献[7]中查取。

1.2海流载荷

海流通常被可看作一种稳定的平面流动，单位长度的海流力表达式可以用以下方程[2]来表示：

(7)

按照稳定流动条件的阻力的数学表达方法，圆柱上的总海流力可表示为

(8)

由于海流流速随着水深会发生变化，在无实测数据的情况下，可以采用美国船舶检验局使用的公式

(9)

式中：Fc为结构单位长度的海流载荷，N/m；Cd为阻力系数，取为0.98；u 为海流最大可能速度；ρw为海水密度，1 025kg/m3；D为圆柱形桩直径，m；Fc为海流作用于圆柱体上的总力，N；d为水深，m；dz为水深方向的长度增量；uch为距离z处的海流速度，m/s；um为海面的风流速度，m/s；uT为海面的潮流速度，m/s；z为计算深度距离海底的高度，m。

1.3海风载荷

已知风压结构物投影面积A，针对高度较低的结构则可将总风力的表达式表示为

F=KKZαvt2A。

(10)

单位面积上柱体受力的表达式

F1=KKZαvt2。

(11)

然而实际风速是沿着高度的增加不断变大的。对于不同高程的风速计算可以采用以下公式：

v(t,z)=v(t,zc)(z/zc)0.125。

(12)

式中：F为风载荷，N；K为风载荷形状系数，圆柱体侧壁取0.5；KZ为海上风压高度变化系数，取为1.0；v为设计风速，m/s；A为受风面积，m2；α为风压系数，取为0.613 N· s2/ m4；t为时间长度，可 为1 s或1 h；zc为最高参考点高度；v(t,z)为所求高度z的风速。

2 工程实例

某浅海油田，隔水导管尺寸参数为：外径0.61 m；壁厚0.02 m。材料参数为：弹性模量209 GPa；泊松比0.28；密度7 850 kg/m3,屈服强度350 MPa。环境参数：水深25 m；海面以上高度15 m，风速35 m/s；最大波高7.6 m；有效周期9.1 s；沿水深方向，每隔6.25 m取一流速值，海面流速1.97 m/s；中部流速1.71 m/s；中部流速1.45 m/s；中部流速1.16 m/s；海底流速0.86 m/s；井口压载26 t。试根据以上数据，采用相关公式求隔水导管上的最大波浪载荷、海流载荷以及风载荷，并拟合出载荷随深度或高度变化的表达式。

2.1波浪力的计算

采用Morison方程计算波浪力，需选用合适的波浪理论和相应的惯性力系数和阻力系数,据壳牌公司拟定的标准取CD=0.578∶CM=1.628。Stokes五阶波理论适用范围为d/L≥0.1，本文d/L=0.22，采用Stokes五阶波理论[3]合理。采用Stokes五阶波理论求解波浪力，关键在于求解海水的速度和加速度。求解海水的速度和加速度的过程繁杂，涉及的未知量纲一参数较多，但各参数求解公式在很多资料[5]中可查到，这里不再作详细介绍。由方程(4)与(5)，运用MATLAB[6]求得L=115.62 m，k=0.054。根据d与L的比值，查阅文献[4]附录可得求解速度与加速度过程的量纲— 参数，以海底平面为x轴方向，建立坐标系，并将以上所查取的量纲一参数带入方程(2)、(3)得速度方程、加速度方程以及波面方程分别为：

ux=2.073 9(1.187 3chkzcosθ+

0.601 8ch2kzcos2θ-0.000 406ch3kzcos3θ-

0.000 047ch4kzcos4θ+0.000 009ch5kzcos5θ)；

(13)

ax=1.4(1.187 3chkzsinθ+0.223 6ch2kzsin2θ-

0.000 42ch3kzsin3θ-0.000 3ch4kzsin4θ+

0.000 059ch5kzsin5θ);

(14)

(15)

式中：x/L为波浪相位；θ=kx-ωt；z为计算点至海底的距离。

由方程(15)可知x=0处，波面取的最大值ηmax=(0.163 4+0.022 6+0.003 8+0.000 666 8+0.000 140 16)/0.054=3.53 m。为计算方便，根据公式(13)和(14)应用Maltlab求最值程序，算得沿深度z向的最大速度与加速度如表1所示。

表1 z向最大速度与加速度分布

MATLAB包含多种工具箱，在数据拟合方面功能比较强大，拟合数据较为准确。由于计算量比较大，不可能将每个点的数值都计算出来，所以可以根据表1中的数据，运用MATLAB中的polyfit命令拟合出最大速度与加速度以及最大波浪力随深度方向变化的函数表达式：

ux=1.661 98+0.002 94z+0.001 95z2+ 0.000 061 109 2z3；

(16)

ax=0.77-0.003 3z+0.001 78z2+ 0.000033z3；

(17)

Fw=638.465 4+28.279 34z- 2.750 79z2+0.241 22z3。

(18)

2.2海流力的计算

在已知不同深度处的海流速度，运用式(7)分别计算不同深度处的波浪力，然后将所得结果进行多项式拟合，求出海流载荷随深度变化的表达式。计算结果见表2。

表2 z向海流流速与海流力

根据表2的数据，进行多项式拟合，得海流力随深度变化的函数表达式

Fc=81.102 29+9.997 19z+0.154 68z2(19)

2.3风力的计算

已知在海面15 m高度处最大风速为35 m/s，根据式(11)和(12)可计算不同高程处风力的大小。根据表3中的数据可拟合出单位长度管端上总风压随高程变化的函数表达式

F2=139.811+44.75z-3.589z2+0.11z3。

(20)

表3 不同高度处风速与风力

3 有限元数值模拟

根据式(18)、(19)、(20)，运用ANSYS Workbench[7]模拟隔水导管在风载荷、波浪载荷、海流载荷和自重作用下的应力分布和形变状况，求出临界屈曲载荷与前4阶固有频率所对应的共振转速。在Workben-ch建立模型，采用六面体主导划分网格，划分结果为单元数为63 286，节点数为132 983。网格划分完毕，在Commands编辑器中插入命令流，建立(18)、(19)、(20)的function载荷函数，并施加到结构所对应的截面上。

图2为Workbench前处理部分所施加的载荷和约束，图3和图4分别为应力分布和变形情况。从图3可看出应力最大位置在结构的固定端，最大值为52.097 MPa，结构在该处受到弯矩作用。图4反映了最大变形位置在距管底23.85 m处的波流共同作用部位，在该处风力最小，波浪载荷与海流载荷最大，由于该处为自由变形，故结构位移在该处达 到了最大值54.019 mm。在结构距管底23.85 m应力为37.149 MPa，虽然结构在该处所受的外力最大，形变位移最大，但所受的应力不是最大的。通过分析结果我们找到隔水导管的2个薄弱环节：1)所受应力最大的隔水导管底端；2)变形最大的风波流联合作用部位。根据实际工程的需要可以将结构在这些部位进行补强。

结构的位移响应除了受外力影响外，还要受到结构钻井机械转动频率的影响，根据模拟结果得到四阶固有频率和屈曲载荷因子，通过理论计算可得与隔水导管共振转速与隔失稳的临界载荷。具体结果见表4。

图2 载荷与约束

图3 应力分布

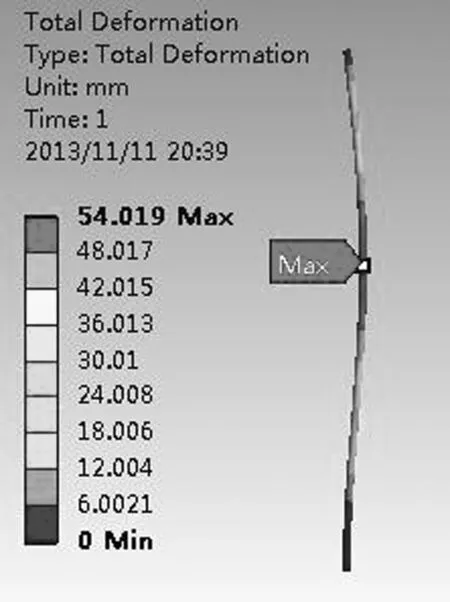
图4 形变情况

表4 隔水导管临界载荷

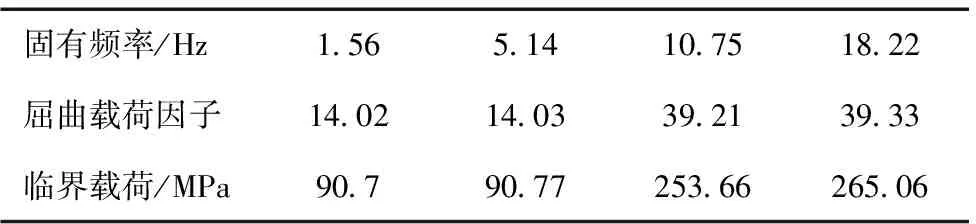
固有频率/Hz1 565 1410 7518 22屈曲载荷因子14 0214 0339 2139 33临界载荷/MPa90 790 77253 66265 06

从表4中可以看到第一阶屈曲载荷因子为14.02，井口压载为25 t(合6.53 MPa)，故可得结构的一阶屈曲压力为6.53×14.02=91.6 MPa。由于第一阶为屈曲载荷的最低值，所以理论上认为当压力达到91.6 MPa时结构将会失稳，该值远远大于井口压载，表明结构屈曲强度足够，可放心使用。根据所得固有频率，同时还可计算出相应的结构共振转速[8]，如表5所示。

表5 隔水导管的共振转速

4 结束语

隔水导管的结构虽然简单，但是所受载荷非常复杂。笔者采用Stokes五阶波理论计算波浪力，与线性波和三阶波理论相比,计算结果能更真实地反映波浪载荷。为尽可能模拟真实海况，结构所施加的波浪力、风力和海流力均为变载荷。通过以上分析得到以下结论。

1)介绍了风、波、流载荷的理论算法，利用ANSYS Workbench 软件模拟了隔水导管在轴向压载和横向梯度载荷作用的屈曲响应，得到了失稳临界载荷和应力与形变分布，确定了结构的薄弱部位。根据工程实际需要可在薄弱环节采取相应防护或加强措施，以提高作业安全性。

2)计算出可能引起隔水导管共振的转速，这些转速在作业过程中应尽量避免，以防止共振破坏。

3)由于实验条件的限制，本文结果无法用实验验证。与实验相比计算机模拟有以下优点：相对实验成本更低，得到结果更快，可以一目了然地看到应力与位移的整体与局部分布情况，这是理论解析和实验所不能得到的。

4)本文计算结果偏保守，强度安全系数大于4，满足实际工程要求。仿真结果表明本例隔水导管在所给定的海况下可以安全使用。

[1]Skjelbreia L,Hendrickson J.Fifth Order Gravity Wave Theory[C]//Seventh Conference on Coastal Engineering. Beijing:ASCE,1961,1:

[2]王树青，梁丙臣.编著海洋工程波浪力学[M].青岛：中国海洋大学出版社,2010：11.

[3]杨进,刘书杰,姜伟，等.ANSYS在石油工程中的应用[M].北京：石油工业出版社，2010：2.

[4]竺艳蓉. 几种波浪理论适用范围的分析[J]. 海岸工程, 1983,2(2):11-27.

[5]竺艳蓉. 海洋工程波浪力学[M]. 天津： 天津大学出版社, 1991.

[6]严克明,欧志英,刘树群.数值计算基础[M].兰州：甘肃人民出版社，2010：5.

[7]李兵,何正嘉,陈雪峰.ANSYS Workbench设计仿真与优化[M].北京：清华大学出版社，2013:3.

[8]姜伟.深水钻井隔水导管挠曲方程及固有频率研究[J].中国海上油气,2011,23(3):17.

(编校：叶超)

TheBucklingSimulationofDrillingRiserinShallowWatersundertheCombinedEffectsofWind,WavesandCurrents

ZHENG Yun-hu,JIANG Feng*

(CollegeofPetrochemicalEngineering,LanzhouUniv.ofTech,Lanzhou730050China)

Force applied to riser is analyzed. As for wind, waves and currents, the relationship between their load and their height and depth is work out. The relationship was applied to oil field engineering in shallow sea. Riser buckling response and stress distribution in the harshest conditions were simulated on Workbench and the critical buckling load deformation characteristics and stress distribution were obtained. The structural weaknesses was pointed out. Corresponding to each order resonance speed, the frequency was calculated with the natural frequency.

drilling riser; buckling analysis; critical load; natural frequency; fifth-order wave

2013-11-26

国家质检公益项目(201210026，201310152)；甘肃省财政厅高校基本科研业务费(1205ZTC067)

：姜峰(1969—)，女，副教授，硕士，主要研究方向为承压设备。

：A

：1673-159X(2015)02-0103-5

10.3969/j.issn.1673-159X.2015.02.021

*