偏差校正的DCT子空间非局部均值MRI图像去噪算法

(西华大学数学与计算机学院，四川 成都 610039)

· 计算机软件理论、技术与应用·

偏差校正的DCT子空间非局部均值MRI图像去噪算法

胡金蓉，王晓明，黄增喜

(西华大学数学与计算机学院，四川 成都 610039)

针对直接采用高斯白噪声去噪算法去除MRI图像中的莱斯(Rician)噪声仅能取得次优去噪效果这一问题，在DCT子空间非局部均值去噪算法基础上，提出一种偏差校正的DCT子空间非局部均值MRI图像去噪算法。首先分析MRI图像中Rician噪声的特性，给出在MRI模值平方图中估计噪声偏差的方法；然后使用偏差校正的DCT子空间非局部均值MRI图像去噪算法在MRI图像的模值平方图上进行去噪处理。在模拟MRI图像上进行实验，其结果表明，该算法在有效去除Rician噪声的同时，很好地保留了器官和软组织的细节纹理信息，取得了较好的去噪效果。

图像去噪；非局部均值；磁共振成像；莱斯噪声

磁共振成像(magnetic resonance imaging，MRI)是利用核磁共振(nuclear magnetic resonance，NMR)机制进行成像的技术[1-2]，是当今医学影像领域极其重要的诊断方法之一。在MRI图像的采集过程中不可避免地会受到随机噪声的影响，使得重建后的MRI图像存在大量的莱斯噪声(Rician noise)以及伪影(artifacts)[3]。噪声降低了MRI图像的视觉质量，限制了对图像进行分割、配准等后续处理过程的性能，降低了对组织内容进行定量分析的准确程度。通过数字图像处理技术消除MRI中的噪声，既不对现有成像过程做任何改变，也不会增加成像所需时间和成本。许多经典的滤波方法已被运用在成像后的处理阶段以改善MRI图像的视觉质量[4-13]。这些方法大体上可以分为3类：以MRI模图像为对象进行处理、以MRI复数图像为对象进行处理和以MRI模平方图像为对象进行处理。第1类方法通常把MRI模图像中的噪声当作加性高斯噪声，但实际上模图像中的噪声是Rician噪声；因此，这类方法往往不能得到好的去噪效果。第2类方法的去噪效果一般要优于第1类方法，因为实部和虚部中的噪声分别都是加性的高斯白噪声，不存在信号和噪声相关项，可以采用所有适合去除高斯噪声的方法对实部和虚部分别进行处理；但容易引起相位畸变，导致相位信息不可用，使重构后的MRI图像中存在因相位误差而产生的“虚影”。第3类方法最先由Nowak[3]提出来，以在MRI模平方图像中信号和噪声的相关性较低为依据进行去噪，可以更容易地从噪声中估计出信号。由于Rician噪声的均值不为零，噪声信号中存在着偏差，因此在MRI模值平方图上可以对Rician噪声的偏差值进行估计，实行带偏差校正的去噪处理，从而可以得到更好的去噪效果。

本文提出一种偏差校正的DCT子空间非局部均值MRI图像去噪算法，将DCT子空间非局部均值去噪算法[14]应用于MRI图像的去噪处理，在MRI模平方图像空间上进行去噪。文章首先分析MRI图像中Rician噪声的特性，给出在MRI模值平方图中估计噪声偏差的方法，然后使用该方法在MRI图像的模值平方图上进行去噪处理。实验结果表明，本文算法既能有效去除Rician噪声，也很好地保留了器官和软组织的细节纹理信息，取得了较好的去噪效果。

1 DCT子空间非局部均值图像去噪

非局部均值去噪方法(nonlocal means， NLM)是Buades等[15]提出的基于图像自身固有的数据冗余特性、利用图像中含有大量重复结构、采用空域加权均值滤波来非线性地进行去噪的过程。它不基于任何正则性假设，具有假设条件弱、表达形式简单、易于实现等优点，其去噪性能不仅优于邻域滤波算法，如双边滤波[16]，也优于各向异性扩散[17]、全变差滤波[18]和基于小波变换的方法[19]等，是当前图像去噪研究中的热点。用u表示未受噪声污染的数字图像，v(i)=u(i)+n(i)表示噪声图像，用Ni表示像素i所在的大小为r×r的图像块，用p(Ni)表示图像块Ni中所有像素灰度值构成的向量，用Si表示以像素i为中心的搜索窗口。该方法对u(i)的估计值定义为

(1)

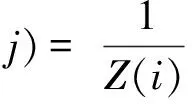
离散余弦变换(discrete cosine transform，DCT)具有良好的能量紧致性，可用少数系数表示图像中主要能量成分，对噪声具有鲁棒性；因此，文献[14]将DCT与非局部均值算法相结合，提出一种DCT字空间的非局部均值去噪算法，其在图像块对应的DCT低频系数子空间中度量像素间的相似性，提升了非局部均值算法的去噪性能。该算法定义为

(2)

当d=M时，该算法与NLM算法等价。

2 偏差校正的DCT子空间非局部均值MRI图像去噪

2.1 MRI图像噪声特性

原始MRI信号是位于K空间内的复数数据，即K空间数据，其实部和虚部分别对应于接收线圈所采集到的MRI信号经过正交验波之后，分成相位差为90°的2部分。由于成像仪器中的磁体、发射线圈、接收线圈以及信号传输线等部件产生的热噪声，这2部分数据中均携带有均值为零、方差为σ2的独立加性高斯白噪声。将K空间中含有噪声的原始MRI信号表示为

VK=(RK+nr)+i(IK+ni)。

(3)

式中：VK为含有噪声的MRI信号；RK和IK表示MRI信号的实部和虚部；nr和ni表示均值为零方差为σ2的独立加性高斯白噪声。

MRI图像重构就是将VK进行傅里叶反变换，得到图像域数据，这些数据的模所组成的图像就是最终看到的MRI图像。重构得到信号的实部和虚部仍然是真实信号和高斯噪声的叠加

vS=(rS+nr)+i(iS+ni)。

(4)

对vS的实部和虚部进行求模，就得到MRI图像信号，即

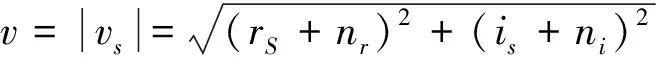
(5)

其中v也被称为MRI的模值图像。式(5)表明i中的噪声已经不再是加性高斯白噪声，而是一种与信号相关的乘性噪声，即莱斯(Rician)噪声，其概率密度函数为

(6)

式中：I0(·)是为零阶修正贝塞尔函数(Bessel function，BeF)；A是信号的幅度值，对应于MRI图像中像素的灰度值；σ2是噪声方差；v是采集到的MRI模值信号。根据莱斯分布的概率密度函数可知，在图像的低信噪比区域(如背景等暗沉区域)，噪声将由莱斯分布退化成为瑞利(Rayleigh)分布，例如，当A/σ等于0时，式(6)所表示的莱斯分布将退化成为瑞利分布

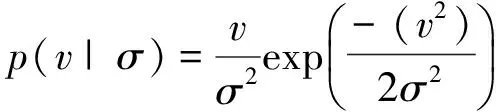
(7)

而在图像的高信噪比区域，噪声将由莱斯分布退化成高斯分布，即

(8)

2.2 MRI图像中偏差值的估计

在式(5)所示的MRI模值图像的基础上，MRI模平方图像可表示为

v2=(|vs|)2=(rS+nr)2+(iS+ni)2。

(9)

对式(9)两端分别求期望整理得

(10)

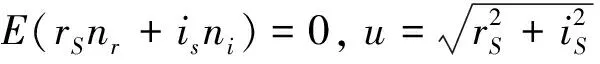
E(v2)=E(u2)+2σ2。

(11)

这表明在MRI模平方图像空间中，真实信号与噪声信号之间存在着2σ2大小的偏差，并且噪声标准差σ可以根据MRI图像中背景区域的值进行估计

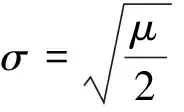
(12)

其中μ是选定的用于估计σ的背景区域内像素点的均值。

2.3偏差校正的DCT子空间非局部均值MRI图像去噪算法描述

偏差校正的DCT子空间非局部均值MRI图像去噪算法(UNLM-DCT)的主要步骤如下。

1)根据式(12)估算出MRI图像中噪声的标准差σ。

2)计算噪声MRI图像v的模平方图像v2。

3)采用NLM-DCT算法对v2进行去噪处理，初步得到去噪后的MRI模平方图像

(13)

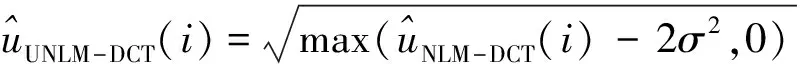
(14)

3 实验结果及分析

以BrainWeb数据库[20]提供的模拟MRI图像数据作为测试图像(即T1加权成像图像、T2加权成像图像和质子密度加权成像图像(proton density，PD)，分别简称为T1图像、T2图像和PD图像，大小为217×181)，根据式(15)—(17)所定义的过程，在测试图像中加入Dh的高斯噪声，得到被噪声水平为3%、6%、9%、12%、15%和18%的Rician噪声污染的MRI实验图像。

vr(i)=u(i)+n1(i),n1(i)～N(0,σ)；

(15)

vi(i)=n2(i),n2(i)～N(0,σ)；

(16)

(17)

其中u表示原始测试图像。原始的T1、T2和PD加权测试图像和含有强度为6%的Rician噪声的实验图像如图1所示。

(a)T1图像

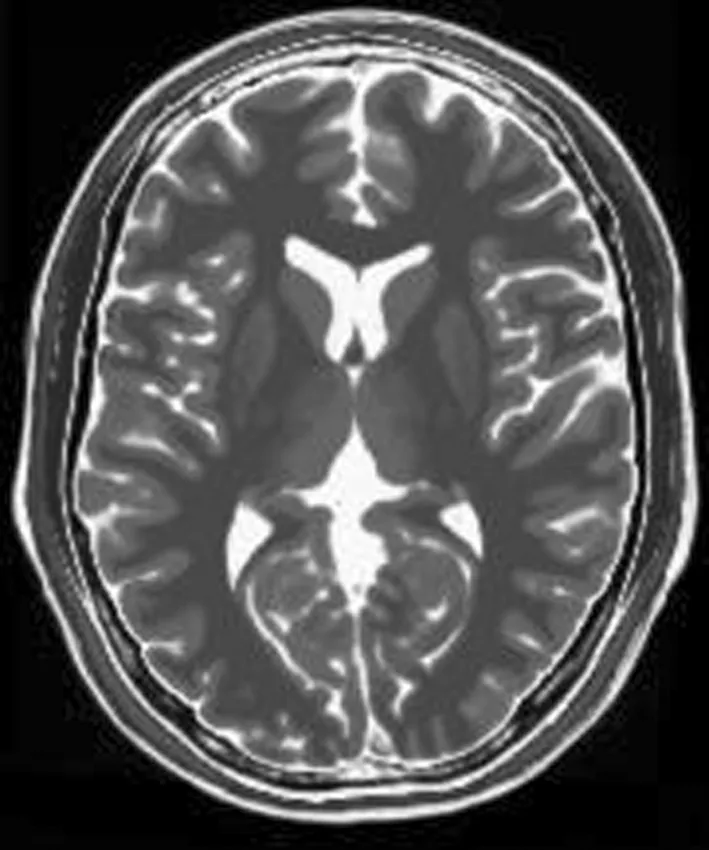
(b)T2图像

(c)PD图像

(d)含有6%莱斯噪声的T1图像

(e)含有6%莱斯噪声的T2图像

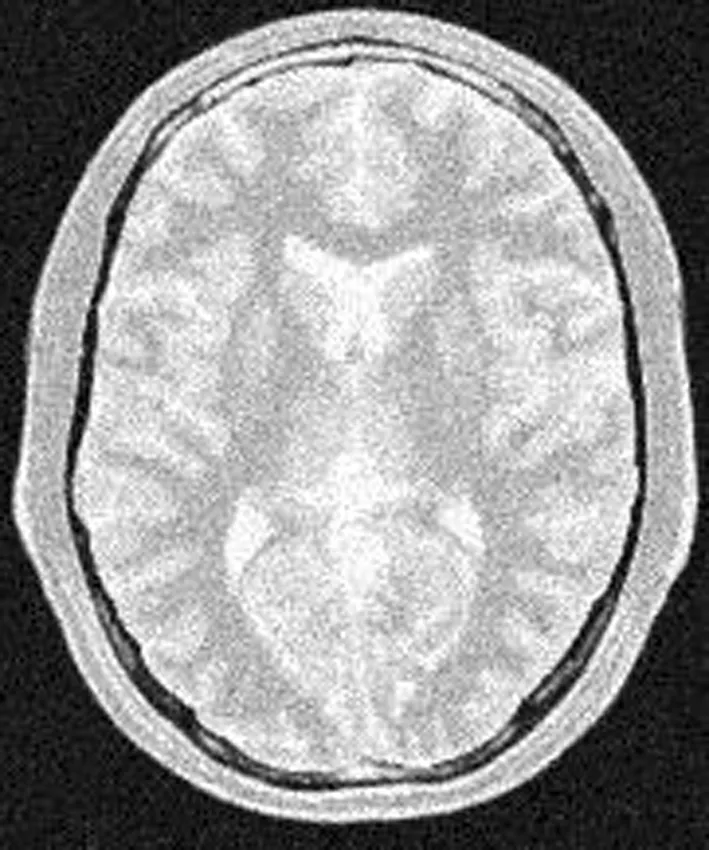
(f)含有6%莱斯噪声的PD图像

图1 MRI测试图像及含有6%莱斯噪声的实验图像

使用本文算法UNLM-DCT、非局部均值算法NLM和无偏非局部均值算法UNLM对上述实验图像进行去噪实验，搜索窗口为11×11，邻域为5×5，DCT子空间维数为8，调节算法的滤波参数v使各算法达到最好的性能。采用峰值信噪比和平均结构相似性准则对滤波效果进行定量比较；根据滤波后图像的主观视觉质量和残余信号对去噪性能进行定性比较。

3.1 PSNR值

表1给出了3种去噪算法对实验图像去噪处理后PSNR值的比较结果，“Noisy”行的数据表示噪声图像的PSNR值。可知：含有偏差校正的UNLM和UNLM-DCT算法的去噪效果好于不进行偏差校正的NLM算法；UNLM-DCT算法的去噪效果又优于UNLM算法。图2给出了这3种算法在PSNR值方面更直观的比较结果。可以看出，当噪声强度较高时(比如12%、 15%或18%)，UNLM-DCT算法的去噪性能明显优于UNLM和NLM算法，将去噪图像的PSNR值几乎提高了1 dB。

表1 3种去噪方法得到的PSNR值比较 dB

(a)T1图像

(b)T2图像

(c)PD图像

3.2视觉质量及残差图像

图3显示了NLM、UNLM和UNLM-DCT算法对被6%的莱斯噪声污染的T1图像进行去噪处理后的结果。其中，图3(e)、(f)和(g)分别是这3种滤波算法对应的残差图像，它们是通过用噪声图像减去滤波后的图像得到的。

从图3(b)(c)(d)可以看出，与NLM和UNLM算法相比，UNLM-DCT算法能够更有效地去除噪声，取得了最好的视觉效果。通过对图3(e)(f)(g)的比较可见，UNLM-DCT算法得到的残差图像中基本不含有原始图像中的结构信息(如组织区域的轮廓以及纹理信息等)，说明该方法能够很好地保护图像中的基本结构及纹理细节信息，这有利于后续的诊断，也有利于分割、配准等后续处理过程的进行。

(a)含6%莱斯噪声的T1图像

(b)NLM算法去噪结果图像

(c)UNLM算法去噪结果图像

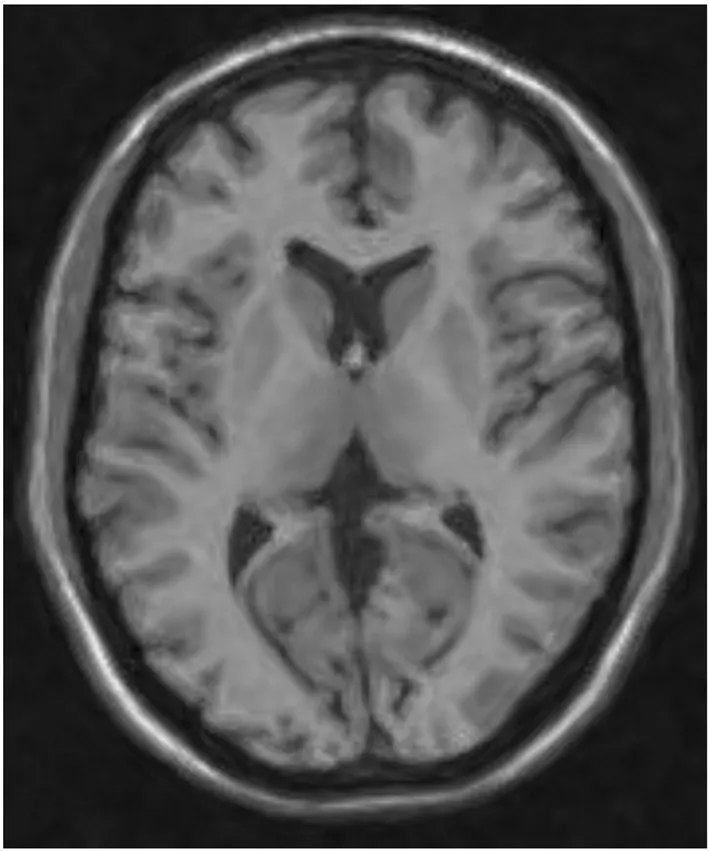
(d)UNLM-DCT算法去噪结果图像

(e)NLM算法残差图像

(f)UNLM算法残差图像

(g)UNLM-DCT算法残差图像

4 结论

MRI图像中的噪声是乘性的均值不为零的莱斯(Rician)噪声，然而现有MRI图像去噪直接采用去除零均值加性高斯白噪声的去噪算法，这样仅能取得次优的去噪效果。本文提出的偏差校正的DCT子空间非局部均值MRI图像去噪算法考虑了MRI图像中Rician噪声的特性，估计出噪声的标准差在MRI模值平方图上进行去噪。实验结果表明了该算法的有效性：在去除噪声的过程中既没有损失掉MRI图像中的组织纹理细节信息，也没有引入新的伪影，取得了很好的去噪效果。

[1]Edelman R R, Warach S. Magnetic Resonance Imaging[J]. New England Journal of Medicine,1993, 328(10):708-716.

[2]Wright G A . Magnetic Resonance Imaging[J]. Signal Processing Magazine, 1997, 14(1):56-66.

[3]Nowak R D. Wavelet-based Rician Noise Removal for Magnetic Resonance Imaging[J]. IEEE Transactions on Image Processing, 1999, 8(10):1408-1419.

[4]Donoho D L. De-noising by Soft-thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3):613-627.

[5]Coupé P.An Optimized Blockwise Nonlocal Means Denoising Filter for 3-D Magnetic Resonance Images[J]. IEEE Transactions on Medical Imaging, 2008, 27(4):425-441.

[6]Gerig G , Kubler O , Kikinis R,et al.Nonlinear Anisotropic Filtering of MRI Data[J]. IEEE Trans Med Imaging,1992, 11(2):221-232.

[7]Fang Z, Lihong M. MRI Denoising using the Anisotropic Coupled Diffusion Equations[C]//Biomedical Engineering and Informatics (BMEI), 2010 3rd International Conference on (Volume：1). Yantai： IEEE,2010： 397-401.

[8]Weaver J B, Xu Y, Healy Jr D，et al. Filtering Noise from Images with Wavelet Transforms[J]. Magnetic Resonance in Medicine,1991, 21(2):288-295.

[9]Zaroubi S, Goelman G.Complex Denoising of MR Data via Wavelet Analysis： Application for Functional MRI[J]. Magnetic Resonance Imaging,2000, 18(1):59-68.

[10]Anand C S, Sahambi J S. Wavelet Domain Non-linear Filtering for MRI Denoising[J]. Magnetic Resonance Imaging,2010, 28(6):842-861.

[11]Wiest-Daesslé N, Prima S, Coupé P, et al. Rician Noise Removal by Non-Local Means Filtering for Low Signal-to-Noise Ratio MRI： Applications to DT-MRI[C]//Proceedings of the 11th International Conference on Medical Image Computing and Computer-Assisted Intervention, Part II. New York： Springer Berlin Heidelberg,2008：171-179.

[12]He L, Greenshields I R. A Nonlocal Maximum Likelihood Estimation Method for Rician Noise Reduction in MR Images[J]. IEEE Transactions on Medical Imaging, 2009, 28(2):165-172.

[13]Manjón J V, Coupé P, Martí-Bonmatí L, et al.Adaptive Non-local Means Denoising of MR Images with spatially Varying Noise Levels[J]. Journal of Magnetic Resonance Imaging,2010, 31(1):192-203.

[14]胡金蓉, 蒲亦非, 张意, 等. DCT子空间的非局部均值去噪算法[J].计算机辅助设计与图形学学报，2012, 24(1):89-96.

[15]Buades A, Coll B, Morel J-M. On Image Denoising Methods[J]. SIAM Multiscale Modeling and Simulation, 2005, 4(2):490-530.

[16]Tomasi C, Manduchi R. Bilateral Filtering for Gray and Color Images[C]//Computer Vision, Sixth International Conference on. Bombay： IEEE,1998：839-846.

[17]Perona P, Malik J.Scale-space and Edge Detection using Anisotropic Diffusion[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1990, 12(7):629-639.

[18]Rudin L I, Osher S, Fatemi E. Nonlinear Total Variation Based Noise Removal Algorithms[J]. Physica D： Nonlinear Phenomena,1992, 60(1/4):259-268.

[19]Strela V, Portilla J，Simoncelli E. Image Denoising Using a Local Gaussian Scale Mixture Model in the Wavelet Domain[C]//Proceeding SPIE Wavelet Applications in Signal and Image Processing VIII. San Diego： SPIE,2000：363-371.

[19]Collins D L. Design and Construction of a Realistic Digital Brain Phantom[J]. IEEE Transactions on Medical Imaging, 1998, 17(3):463-468.

[20]Kwan R K, Evans A C, Pike G B. MRI Simulation-based Evaluation of Image-processing and Classification Methods[J]. IEEE Transactions on Medical Imaging, 1999, 18(11):1085-1097.

(编校：饶莉)

ABiasCorrectedMRImagesDenoisingMethodUsingDCT-basedNonlocalMeansFilter

HU Jin-rong, WANG Xiao-ming, HUANG Zeng-xi

(SchoolofMathematicsandComputerEngineering,XihuaUniversity,Chengdu610039China)

The noise in MRI image is a multiplicative noise with non-zero mean and obeys Rician distribution. However, many existing MRI image denoising algorithms directly apply methods which are right for additive white Gauss noise with zero mean. They denoise sub-optimally. An optimal bias corrected MR images denoising approach is present based on non-local means filter in DCT sub-space. Firstly, the characteristics of Rician noise in image are analyzed and the method to estimate noise bias in the space of squared magnitude MRI image is discussed. Then, the proposed MRI image denoising algorithm is utilized to reduce the Rician noise. Validation work is carried out on simulated images and the results demonstrate that the proposed method can denoise effectively and it can retain anatomical structures of organs and tissues while remove Rician noise in image.

image denoising; non-local means; magnetized resonance imaging; Rician noise

2014-05-05

国家自然科学基金(61303126)；教育部春晖计划(12226530);西华大学重点科研基金项目(Z1222625)；四川省网络智能信息处理高校重点实验室(szjj2013-022, szjj2012-028)。

胡金蓉(1983—)，女，讲师，博士，主要研究方向为图像处理、模式识别。E-mail:dewhjr@hotmail.com

TP391

：A

：1673-159X(2015)02-0010-6

10.3969/j.issn.1673-159X.2015.02.003