顾前脉冲非线性关联系统的模约束弦稳定性
徐晓惠1,张继业
(1. 西华大学汽车与交通学院,四川 成都 610039;2. 西南交通大学牵引动力国家重点实验室,四川 成都 610031)
·基础学科·
顾前脉冲非线性关联系统的模约束弦稳定性
徐晓惠1,张继业2
(1. 西华大学汽车与交通学院,四川 成都 610039;2. 西南交通大学牵引动力国家重点实验室,四川 成都 610031)
为给自动化公路系统车辆编队控制器设计提供理论基础,本文研究一类具有脉冲干扰的无限维顾前非线性关联系统的模约束弦稳定性。模约束弦稳定性不仅可以保证系统状态的稳态稳定性,同时也给出了系统状态在趋于稳态过程中系统各状态变量的模之间的大小关系。本文在假设各孤立子系统稳定的前提下,基于矢量Lyapunov函数方法并结合数学归纳法,给出确保该系统模约束稳定的充分条件;利用数值算例验证所得结论的正确性和可行性。
关联系统; 无限维; 稳定性; 模约束; 脉冲干扰
在工业实际中,许多复杂系统的控制问题都可转化为关联系统的稳定性问题进行研究[1]。以自动化高速公路系统顾前车辆编队跟随控制系统为例,控制规律的设计是以该关联系统的弦稳定性为前提条件。类似的系统还有飞行编队控制系统[2]、水下机器人编队控制系统[3]等。目前,关于这类复杂系统的弦稳定性研究已经有了一些成果[4-8]。文献[4-8]中的稳定性结论只能保证系统的稳态稳定性。文献[9]以顾前车辆跟随系统为应用背景,提出了一种新的稳定性概念,即模约束稳定性。模约束稳定性是弦稳定性的推广,可以应用于消除误差传递,使关系系统具备更好的控制效果。关于复杂关联系统模约束稳定性的一些现有研究成果可参见文献[9-12]。在实际系统中,不可避免地存在一些不确定性因素,如脉冲干扰、随机干扰等。目前关于具有随机干扰或者脉冲干扰关联系统的弦稳定性问题已经取得了一些研究成果[5-8]。但是文献[5-8]均没有研究系统的模约束稳定性问题。文献[9-11]虽然研究了一些顾前关联系统的模约束稳定性问题,却没有考虑脉冲干扰问题,并且文献[9-10]所得到的模约束稳定性条件是隐式的,不便于实际应用。
基于以上分析,本文以自动高速公路顾前车辆跟随系统为应用背景,从中抽象出一类顾前非线性关联系统,并在模型中考虑脉冲干扰因素。进而利用矢量Lyapunov函数和数学归纳法,研究该系统的模约束弦稳定性。
1 模型描述
首先引入几个记号:‖f(.)‖表示f的Euclidean 范数,‖fi(t)‖=supt≥0‖fi(t)‖,‖f(0)‖=supi∈N‖fi(0)‖,Ν表示自然数集。
一类具有脉冲干扰的无限维非线性关联大系统可由如下方程描述:
其中:xi∈Rn,对于任意i≤j,xi-j=0,i,j∈N;fi:Rn×Rn×…×Rn→Rn,且有fi(0,0,...,0)=0。Δxi(tk)表示tk时刻的脉冲,这里k∈Ν,离散集{tk}满足0≤t0 系统(1)的孤立子系统为 (2) 其中i,k∈Ν。 定义3 假设系统(1)的原点xi=0(i∈Ν)是弦指数稳定的,且对于i=2,3,…,下面不等式是成立的: ‖xi(t)‖≤maxi-r+1≤j≤i-1‖xj(t)‖, t>0,则称系统(1)的原点xi=0 (i∈Ν)是模约束弦指数稳定的。 假设 A1函数fi满足全局Lipschitz条件,即存在正常数lij,1≤j≤r,使得 ‖fi(y1,y2,…,yr)-fi(z1,z2,…,zr)‖≤ 假设 A2对于每个孤立子系统(2),存在一个正定函数Vi=Vi(t,xi(t))以及正常数αil,αih,αi1以及αi2,使得下面的不等式是成立的: αil‖xi(t)‖2Vi(t,xi(t))≤αih‖xi(t)‖2, -αi2‖xi(t)‖2。 引理1[13]假设Vi=Vi(t)≥0,t≥0,i∈Ν。考虑如下不等式: (3) 对于Vi>0,有gi(·)>0。令βi0>0,βij≥0且βij=0(当j≥i时),mii≤mij,i,j=1,2,…。 若存在V=(V10,V20,…),使得 (4) 其中i=1,2,…,且infi{Vi0}=α>0,supi{Vi0}=β>0,那么对于任意给定的ε>0,∃δ>0,使得 ‖V(0)‖<δ⟹supi‖Vi(t)‖<ε。 下面将分析确保系统(1)模约束弦指数稳定的充分条件。 (5) 其中,对于∀i,j=1,2,…,有αih/αil≥1,那么系统(1)的零解是模约束弦指数稳定的,且指数收敛率为0.5(λ-η)。 证明令Wi(t)=eλtVi(t),i∈Ν。 为了简便,在不混淆的情况下,记Wi(t)=Wi,Vi(t)=Vi。 根据假设A2,当t≠tk,k∈Ν时,计算Wi沿系统(1)的右上导数,得到 fi(xi(t),xi-1(t),...,xi-r+1(t))≤ λeλtαih‖xi(t)‖2-αi2eλt‖xi(t)‖2+ ‖xi(t)‖e0.5λt{e0.5λt(λαih-αi2)‖xi(t)‖+ (6) k∈Ν。显然当Ui≠0时, ‖xi(t)‖≠0,i=1,2,…。 不等式(6)可以进一步转化为如下形式: (7) 考虑到(5)式蕴含着下式成立: 进而,当取U=(1,1,...)时,D+Ui<0。根据引理1可知,对于任意给定的ε0>0,存在δ0>0,使得 ‖U(0)‖<δ0⟹supi‖Ui(t)‖<ε0。 由于αil>0,取ε>0,满足ε0=αilε2。对于ε0,存在δ0=αihδ2,当supi‖xi(0)‖<δ时,有 进而 supi(‖Ui(t)‖)2=supi‖Vi(t)‖eλt<ε0, 即对于i=1,2,3,…,有 supi‖xi(t)‖< (ε0/αil)0.5e-0.5λ t=εe-0.5λ t。 (8) 接下来采用数学归纳法证明当脉冲干扰存在时,系统(1)的零解的稳定性。 首先需要证明下面的不等式成立: supi‖xi(t)‖, 即对于tk-1≤t (9) 假设对所有的p=1,2,…,k,tp-1≤t (10) 当t=tk,利用假设A3可以得到 tk-1≤t≤tk。 (11) 可以看出(11)式蕴含下式成立: tk≤t (12) 若式(12)不成立,则必然存在某个子系统i和时刻t*∈[tk,tk+1)使得 (13) 成立,且有D+Wi(t*)≥0,以及 t∈[tk,t*],j=1,2,...,i-1。 (14) 将式(13)和(14)代入到式(6)中,得到 由于(5)式蕴含着下式成立: 因此D+Wi(t*)<0,这与假设D+Wi(t*)≥0矛盾,因此(12)式是成立的,即下面的不等式成立: supi‖xi(t)‖。 supi‖xi(t)‖ e0.5η(t1-t0)e0.5η(t2-t1)…e0.5η(tk-1-tk-2)εe-0.5λt≤ εe-0.5(λ-η)t。 (15) 下面将证明系统(1)零解是模约束稳定的。 当t≠tk,k∈Ν时,经过分析有: -αi2‖xi(t)‖2+αi1‖xi(t)‖· [li,i-1‖xi-1(t)‖+li,i-2‖xi-2(t)‖+…+ li,i-r+1‖xi-r+1(t))]≤ ‖xi(t)‖{-αi2‖xi(t)‖+ ‖xi(t)‖{-αi2‖xi(t)‖+ 令 αil‖xi‖2≤Vi(xi),t≠tk。 令 故‖xi(t)‖ ‖xi(t)‖ (16) 考虑到定理条件,容易看出0 接下来分析当脉冲发生时,系统(1)的零解仍然是模约束稳定的。 由前面的分析可知: ‖xi(t)‖ (17) 由假设A3可知 max{‖‖}≤ (18) 将式(18)代入到式(17),有 (19) 由式(16)和式(19)可知系统(1)的零解是模约束稳定的。 综合式(15)、(16)和(19)可以得出结论:系统(1)的零解是模约束弦指数稳定的。 证毕。 考虑如下脉冲关联系统: (20) 其中xi∈R2表示第i个子系统的状态,令 xi(t)=(xi1(t),xi2(t))T,i=1,2,3,4。 令fi=(fi1,fi2)T,且 f11(x1,0,0)=-12x11, f12(x1,0,0)=-8x12, f2j(x2,x1,0)=-10x2j+0.8x1j, f3j(x3,x2,x1)=-9x3j+0.6x2j+0.3x1j, f4j(x4,x3,x2)=-8x4j+0.5x3j+0.2x2j。 其中j=1,2。显然fi,i=1、2、3、4,满足Lipschitz条件,且l21=10,l22=0.8,l31=9,l32=0.6,l33=0.3,l41=8,l42=0.5,l43=0.2。假定α21=α31=α41=1,α22=30,α32=35,α42=40,α2l=α3l=α4l=1,α2h=2,α3h=3,α4h=4。 容易验证假设A1—A3是满足的。将以上参数代入到定理1中的判定条件,可得: 当i=2时, 当i=3时, 当i=4时, 综上,系统(20)满足定理1的所有条件,因此根据定理1可知该系统的零解是模约束弦指数稳定的,且指数收敛率为0.4。 本文研究了一类具有脉冲干扰的无限维顾前非线性关联系统的动态行为。利用矢量Lyapunov函数法以及数学归纳法,得到了确保该系统模约束指数稳定的充分条件,并给出了指数收敛速度。本文所得的结论可为自动车辆跟随系统、飞行编队系统以及水下机器人编队系统等顾前系统的控制器设计提供一定的理论依据。最后通过数值算例验证了所得结论的正确性和可行性。 [1]Siljak D D. Large-Scale Dynamic Systems Stability and Structure [M]. North-Holland: Amstrerdam, 1978. [2]Zhou J, Peng H. Range policy of Adaptive Cruise Control Vehicles for Improved Flow Stability and String Stability [J]. IEEE Transactions on Intelligent Transportation Systems, 2005, 6(2): 229-237. [3]SchultzA C, Parker L E.Multi-Robot Systems: From Swarms to Intelligent Automata[M]. Dordrecht/Boston/London:Kluwer Academic Publishers, 2002. [4]Swaroop D, Hedrick K.String Stability of Interconnected Systems [J]. IEEE Transactions on Automatic Control, 1996, 41(3): 349-357. [5]Socha L.Stochastic Stability of Interconnected String Systems [J]. Chaos, Solitons and Fractals, 2004, 19(4): 949-955. [6]施继忠, 张继业, 徐晓惠, 时滞随机关联系统的群稳定性[J].自动化学报, 2010, 36(12): 1744-1751. [7]Pan L J, Cao J D.Exponential Stability of Impulsive Stochastic Functional Differential Equations [J]. Mathematical Analysis and Applications, 2011, 382(2): 672-685. [8]Shi J Z, Zhang J Y.String Stability of Infinite-dimension Stochastic Interconnected Large-scale Systems with Time Varying Delay [J]. International Journal of Systems Science, 2014, 45(5): 1035-1041. [9]Pant A, Seiler P ,Hedrick K.Mesh Stability of Look-ahead Interconnected systems [J]. IEEE Transactions on Automatic Control, 2002, 47(2): 403-407. [10]Pant A, Seiler P, Koo T J, et al. Mesh Stability of Unmanned Aerial Vehicle Clusters [C]//In Proceedings of the American Control Conference, 2001: 62-68. [11]Zhang J Y, Suda Y,Iwasa T.Vector Liapunov Function Approach to Longitudinal Control of Vehicles in a Platoon [J]. JSME International Journal: Series C, 2004, 47(2): 653-658. [12]Xu X H, Zhang J Y, Tang L.String Exponential Stability with Mode Constraint of Stochastic Vehicle Following Systems [J]. ASME Journal of Dynamic Systems, Measurement, and Control, 2013, 135(6): 061011. [13]张继业,杨翊仁,曾京.无限维关联系统的弦稳定性[J]. 应用数学和力学, 2000, 21(7): 715-720. (编校:叶超) StringStabilitywithModeConstraintofLook-aheadNonlinearInterconnectedSystemswithImpulsiveDisturbance XU Xiao-hui1, ZHANG Ji-ye2 (1.SchoolofAutomobile&Transportation,XihuaUniversity,Chengdu610039China;2.NationalTractionPowerLaboratory,SouthwestJiaotongUniversity,Chengdu610031China) In order to provide the theory foundation for vehicle formation controller design of automated highway system, in this paper some researches on the stability with mode constraint of a class of infinite-dimensional look-ahead nonlinear interconnected systems with impulsive were studied. Intuitively the string stability with mode constraint not only can guarantee the stability of steady-state of the system but also give the size relationship of the state variables when the system converges to steady-state process. Under the condition that the isolate subsystems were stable, some sufficient conditions ensuring the string stability with mode constraint of the system were obtained by using the vector Lyapunov function method and mathematical induction. A numerical example with simulations was given to show the correctness and practicability of the obtained results. interconnected system; infinite-dimensional; stability; mode constraint; impulsive disturbance. 2014-03-29 国家自然科学基金资助项目(11402214,11172247,51375402,61273021);新能源汽车电控技术四川省青年科技创新研究团队(2015TD0021);西华大学重点科研基金项目(zl320312) 徐晓惠(1982—), 女, 讲师, 博士,主要研究方向为复杂系统的稳定性分析与控制。 TP13; O211.6 :A :1673-159X(2015)04-0047-05 10.3969/j.issn.1673-159X.2015.04.0102 基本定义和假设






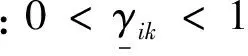

3 主要结论
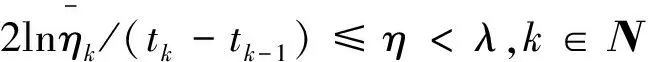
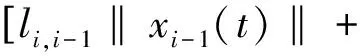
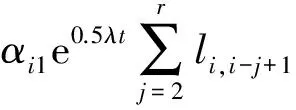




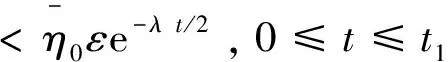













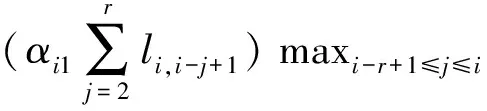

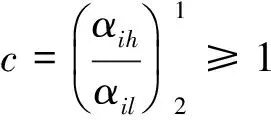


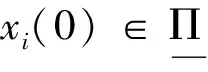




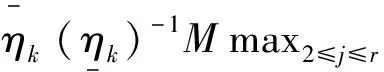
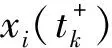
4 数值算例
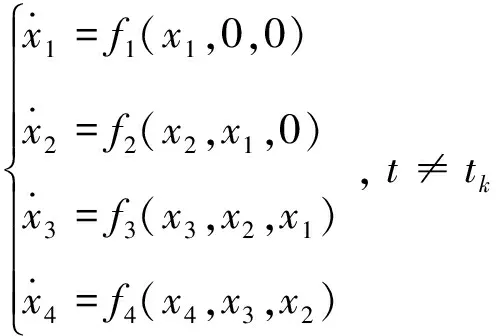
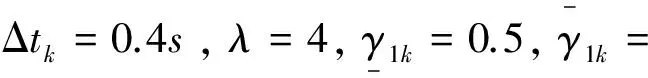

5 结论

