平面截圆柱生成截口曲线为椭圆的相关问题

陈丽萍　彭思言　吕慧明

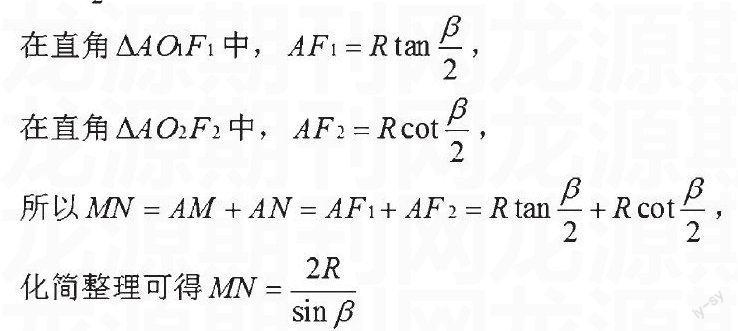
【摘要】比利时数学家丹德林于1822年就已给出了平面截圆锥生成截口曲线为椭圆的证明方法。用丹德林的方法可以证明，用一个平面去截圆柱，得到的截口曲线也是椭圆。本文在其基础上，更进一步，寻找到了椭圆中的定值与截面和圆柱之间明确的数量关系。此结论对于中学生进一步学习椭圆有很大的帮助。

【关键词】椭圆 常数 影响因素

【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089（2015）03-0253-02

我们已经熟知，平面内到两定点距离之和等于常数（大于两定点间的距离）的点的轨迹叫做椭圆。椭圆与科研、生产以及人类的生活有着密切的关系。例如，天体中一些行星运行的轨道是椭圆，一些电影放映灯泡反射镜面的横截面就是椭圆的部分。又如在圆柱形的试管中盛一半水，将试管倾斜一个角度，水面的边界就是椭圆。

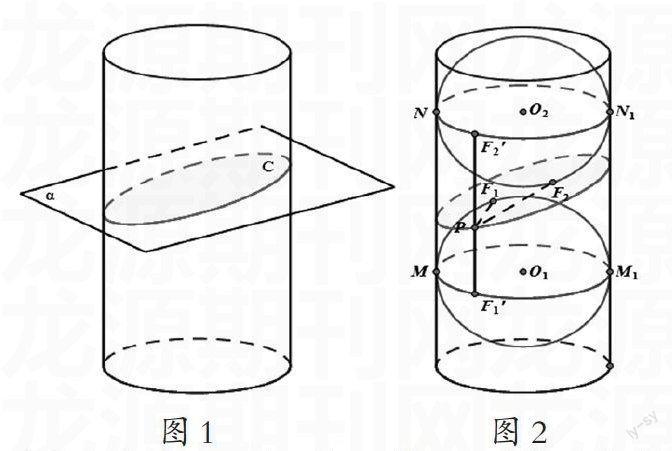
那么，水面的边界为什么就是一个椭圆呢？我们可以从实际问题中抽象出数学模型，然后做进一步的研究。可将试管抽象成圆柱体，将水面抽象成一个平面，水面的边界就是平面与圆柱体相交生成的截面曲线。如图1所示：

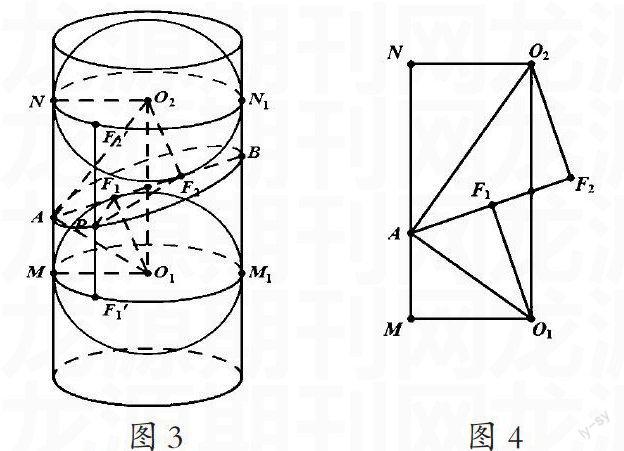
我们不妨先做一些预备工作。如果将一个球放入圆柱内，且它的半径与圆柱面的底面半径相等，那么球与圆柱的交线为一个圆，就说该球与圆柱相切。如图2，我们把两个球O1，O2放入圆柱内，使他们位于平面α的两侧，且每一个球既与圆柱相切，又与平面α相切，像这样的球称为丹德林球。已知球O1，O2与平面α分别切于点F1和点F2，取截面曲线C上任意一点P，连接PF1，PF2。过点P的圆柱的母线交圆MM1于F1'，交圆NN1于F2'。由于PF1， PF1'同是球O1的切线，所以有PF1= PF1' ，同理PF2= PF2'

F1' F2' 为一常数，且大于F1 F2，由椭圆的定义，可知平面斜截圆柱面时，生成的截面曲线是椭圆[1]。

我们只知道F1' F2' 的长度为一常数，这一常数与截面和圆柱的哪些要素有关呢？是否有具体的数量关系呢？不妨在图2的基础上做一些辅助线，得到图3：

通过图3可知，F1' F2' = MN，因此我们只需再研究常数MN 的长度与截面和圆柱的哪些要素有关。为简化图形，抽取出平面MO1O2N ，标出相应的点和线，得到图4。其中A为椭圆长轴与圆柱母线的一个交点，不难得到一定的数量关系和位置关系。设圆柱面的底面圆半径为R，则有 O1 M=O1 F1=O2 F2=O2 N=R，还有 O1 F1⊥AF1，O2 F2⊥AF2。接下来，再设平面与圆柱面的轴所成的角为β，即∠NAF2=β ，由三角形全等易知，。

通过上式，我们知道平面斜截圆柱生成截口曲线为椭圆中的这一常数与圆柱的底面半径有关，还与圆柱母线和截平面的夹角有关，它们之间存在着明确的数量关系。当二者为一定值时，截口曲线上任意一点到两定点的距离之和为一常数，所以截口曲线为椭圆。用控制变量法可进一步分析，用平面去斜截两个底面不同的圆柱，当截平面与圆柱母线的夹角相同时，圆柱底面半径大的这一常数就大，反之，圆柱底面半径小的这一常数就小。如果用不同平面斜截同一个圆柱，此时圆柱母线与截平面的夹角不相同，根据正弦函数的特点，不妨只看二者所形成的那个较小的角。夹角在，夹角小的对应的常数值反而大，夹角大的对应的常数值反而小。如果圆柱的底面半径不同，夹角也不同，那么就要通过具体的数量关系计算了。

参考文献

[1] 普通高中课程标准实验教科书《数学》A版选修1-1.北京：人民教育出版社，2007年2月第三版