由谐振动动力学特征导出运动方程的一种简明方法
付志扬
(河北省衡水中学 河北 衡水 053000)
1 问题的提出——简谐振动课后的困惑
高二阶段物理课上学习过简谐振动后,奥赛班的学生对简谐振动的运动学方程如何从动力学特征导出产生了浓厚兴趣.但课下查阅大学数学、物理教材和有关文献后,发现受数学知识所限很难理解其给出的推导方法.文献[1]就弹簧振子等模型阐述了谐振动原理和参数的相互关系,列出动力学特征方程后略过求解过程,直接给出解.文献[2]在微分方程一章中,基于二阶常系数齐次线性微分方程理论,以求特征方程、共轭复根的方法,从动力特征方程导出运动学方程,其他教材和文献采用的方法与此方法大同小异.其求解过程简洁,但方法背后的原理如通解、欧拉公式求导、特征方程等远超出中学数学教学大纲,致使高中物理、数学奥赛班的学生也很难理解和掌握.通过机械能守恒定律、势能曲线、微分方程求解,也能导出谐振动运动学方程[3,4],但这种方法绕开了动力学特征,对动力学特征方程和运动学方程的关系不能给出解释.
针对常规推导方法的不易被理解和高中学生现有数学基础的局限性,本文以高中阶段就已学过的运动学、动力学、复合函数求导、简单积分为基础,给出了一种简明易懂的简谐振动运动学方程推导方法,不仅能够使高中学生深刻体会简谐振动的内在原理,还有助于加深理解微积分思想及其在物理学中的运用.
2 简谐振动的动力学特征
以弹簧振子为例,讨论无阻尼简谐振动的特征和运动规律.设平衡位置为坐标原点,按照胡克定律,物体所受的弹性力F与弹簧的伸长即物体相对于平衡位置的位移x成正比,即
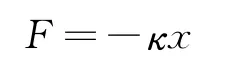
式中κ是弹簧的劲度系数,负号表示力与位移的方向相反.根据牛顿第二定律,物体的加速度a为
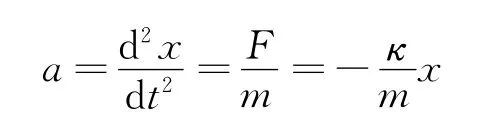
弹簧振子的κ和m都是正值常量,取

代入上式得

式(1)称为简谐振动的动力学特征方程.而高中阶段物理课程直接给出了简谐运动的运动学方程即位移表达式

如何从简谐振动的动力学特征方程导出运动学方程,即如何从式(1)推导出式(2),正是很多高中学生急欲求知的问题.式(1)为二阶常系数线性齐次微分方程,此类微分方程的通常解法是列出特征方程,求出特征方程的两个根,根据两个根的不同情况写出微分方程的通解.求解步骤虽简单,但其背后的原理复杂,解题思想高中阶段难以理解.
3 基于简单微积分的运动学方程推导方法
基本思想是避开高中阶段还未涉及的微分方程及其特征方程、通解等理论,仅应用导数、微分和积分等简明易懂的理论推导和求解.
3.1 方法的思想和步骤
式(1)是二阶导函数且右端只含有因变量x,不明显的含有自变量t,无法直接通过导数微分转换和分离变量求解积分.1728年,欧拉曾考虑了一类二阶微分方程,通过引入新的变量和指数函数,利用变量替换将它转换为一阶微分方程,这是最早的二阶微分方程系统研究[5].这里需要避开微分方程理论及指数函数,但考虑无阻尼谐振动动力学特征方程的特殊形式,很容易通过变量替换对方程进行微分降阶,进而通过简单的分离变量和积分知识求解.
(1)根据运动学物体的位移、速度、加速度和时间的关系式,利用复合函数的求导法则,把位移对时间的二阶导函数转化为速度及其对位移一阶导数乘积的形式,实现二阶微分降阶为一阶微分,x对t的导函数转换为v对x的导函数.
(2)通过分离变量x和v,形成位移微分和速度微分的等式,等式两端再积分后,求得速度对位移的函数关系.此为第一次变量分离和积分.
(3)由位移对时间的导数替代(2)中的v,再通过分离变量x和t,形成位移微分和时间微分的等式,两端积分后,求得位移对时间的函数关系,即简谐振动的运动学方程.此为第二次变量分离和积分.
3.2 方法应用
根据导数和运动学知识,物体运动的位移x,速度v和加速度a有如下关系
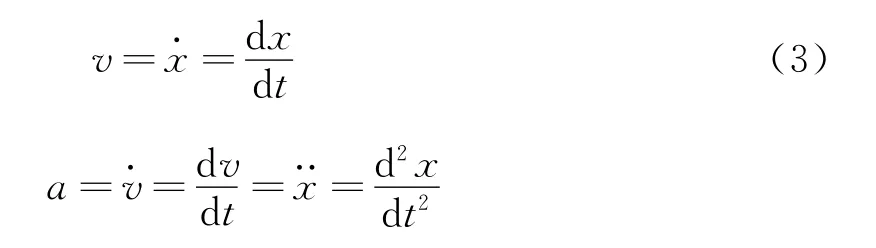
利用复合函数的求导法则并结合上式,把位移对时间的二阶导数转化为速度及其对位移一阶导数乘积的形式,即
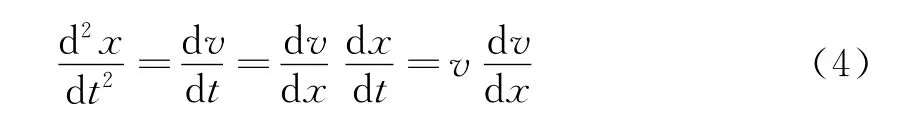
因此,式(1)可转换为

从式(1)转换为式(5)的意义在于,把二阶导函数降阶为一阶导函数,同时把x对t的导函数转换为v对x的导函数,为求解v和x的函数关系创造条件.
将式(5)分离变量,化为微分形式并两端积分

求解积分,得
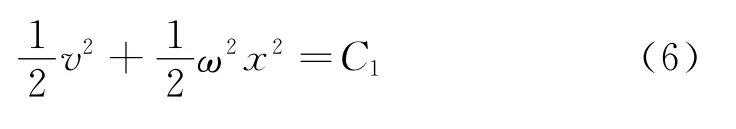
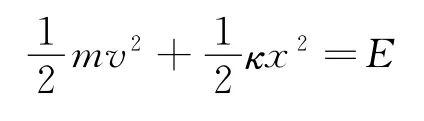
上式中E=mC1为总的机械能分别为动能和弹性势能.
引入常量A2替换常量,将式(6)变形为

根据初始条件位移为x0,速度为v0,可确定常量A

根据式(7)解得
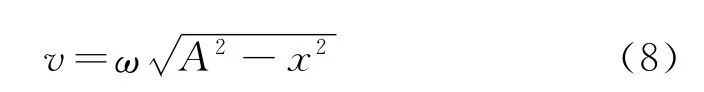
将式(3)代入式(8)
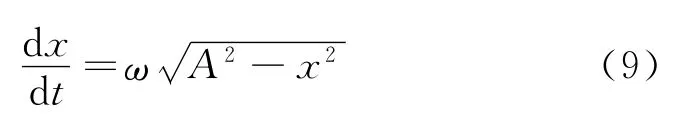
将式(9)转换成微分形式并两端积分

因

所以
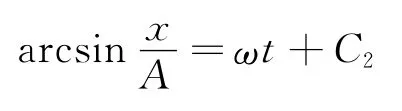
根据初始条件位移为x0,时间t=0,可确定出常数C2的值
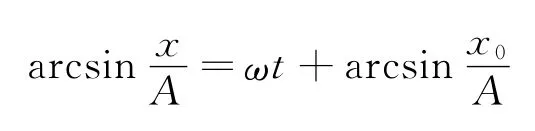
上式即为式(2)给出的简谐振动运动学方程的标准形式,式中A为振幅,ω为角频率,φ0为初相位.通过上述推导,简谐振动中各个特征量的物理、数学意义及相互关系也更加清晰.
3.3 方法的适用性
上述方法还适用于同为简谐振动的LC震荡电路中电流随时间变化的规律推导.一般情况下对于型的动力学特征方程求解问题仍然适用,亦即加速度函数仅明显含有位移变量、不明显的含有时间变量的情况,如万有引力场、点电荷电场中物体或带电粒子的速度、位移求解问题.
【例题】带正电量Q的点电荷固定在长度为2l的绝缘平直光滑轨道左端,带正电量q,质量为m的粒子从轨道中点由静止释放.假设带电粒子除电场力外不受其他外力作用,求带电粒子位移随时间变化的运动学方程和从轨道右端滑出时的速度.
求解过程:取连结点电荷和带电粒子的直线为x轴,其方向水平向右,取点电荷为坐标原点.
设t时刻带电粒子的位置则速度和加速度分别为
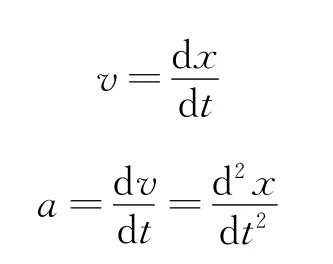
根据库仑定律和牛顿第二定律,得
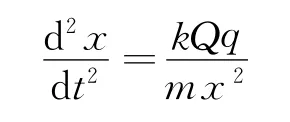
根据式(4)进行微分降阶并分离变量、两端积分
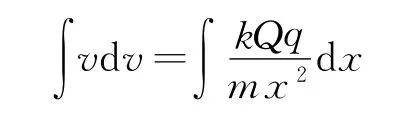
求解积分,得

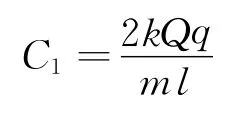
所以
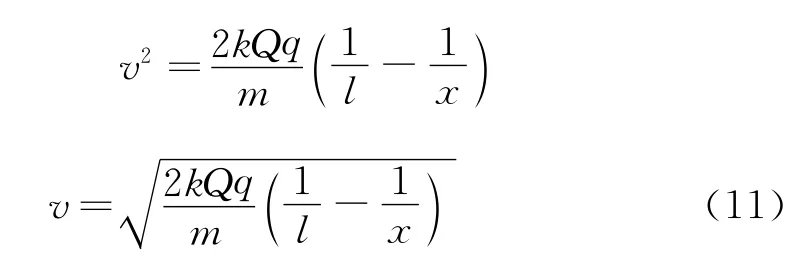
带电粒子从轨道右端滑出时,x=2l,代入上式,即可求得带电粒子滑出轨道时的速度
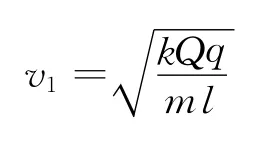
将式(11)中的v用表示,并进行分离变量和两端积分
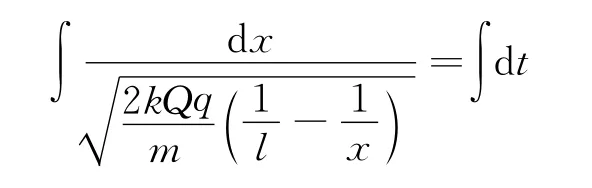
通过换元法令x=lsec2α,对上式积分求解
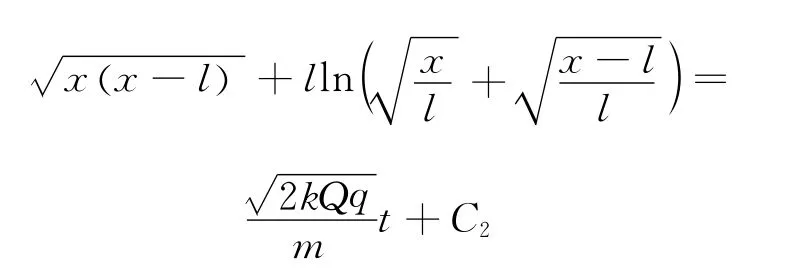
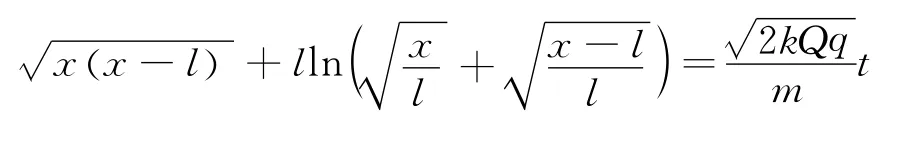
4 结束语
简谐振动极大地促进了近代数学和物理学融合发展[5],学习理解从谐振动动力学特征方程导出运动学方程的数学原理和过程,对高中阶段微积分、三角函数、运动学、动力学、电磁场的系统学习和融会贯通都很有帮助,本文给出的方法具有如下作用:
(1)避开了微分方程理论,通过简明易懂的微分降阶、变量替换、变量分离和积分求解,从动力学特征方程导出简谐振动运动学方程,能够被高中生理解,可用于课上讲解,激发学生向更高层次学习的求知欲.
(2)将微积分思想贯穿始末,能够启发高中生运用近现代数学思想建模和解决物理问题.推导过程串联了运动学、动力学、能量守恒、微积分、三角函数等重要知识点,有助于数学、物理学科融会贯通.

1 程守珠,江之永.普通物理(下).北京:高等教育出版社,2006.2~6
2 同济大学数学系.高等数学(上).北京:高等教育出版社,2007.335~336
3 蔡群,刘燕.简谐振动运动方程的推导.蒙自高等师范专科学校学报,2001(2):4~6
4 胡济通.简谐运动的能量、圆频率以及振动方程的确定.物理教师,2002(08):12~15
5 (美)莫里斯·克莱因.古今数学思想(第二册).张理京,张锦炎,江泽涵,等译.上海:上海科学技术出版社,2014.70~82

