极性晶体膜中强耦合激子的性质

杨洪涛，冀文慧，胡文弢，呼和满都拉

(内蒙古集宁师范学院物理系，乌兰察布012000)

1 引 言

随着分子束外延等新技术的发展和半导体制造业的兴起，极性膜、量子阱和超晶格等低维量子结构［1-5］的研究引起了人们极大的关注［6］. 由于极性膜的很多性质都与膜中激子有关，因而激子的性质一直是人们十分感兴趣的课题. 文中作者等人［7］及许多学者对激子的性质进行了大量的研究［8-11］. 但以往对极性晶体膜的理论工作中，在研究激子与声子相互作用时，只限于讨论激子与表面光学声子相互作用(纯二维情形)或只讨论激子与体纵光学声子相互作用(纯三维情形). 当同时考虑激子与表面和体纵光学声子相互作用时，又都只限于讨论激子-表面光学声子和激子-体纵光学声子均为弱、中耦合情形. 本文采用改进的线性组合算符及Lee-Low-Pines(LLP)变分的方法研究了极性晶体膜中激子与体纵光学(LO)声子弱耦合、与表面光学(SO)声子强耦合系统的性质，讨论了极化子效应和温度对该系统强耦合激子的影响.

2 理论计算

考虑一厚度为2d 的极性晶体膜，膜处于|Z|≤d 的空间，而在|Z|＞d 的空间为真空. 如下图所示，在有效质量近似下，膜中激子-声子相互作用系统的哈密顿量可以写为［12］

图1 半导体膜的几何形状Fig. 1 Geometry of semiconductor slab

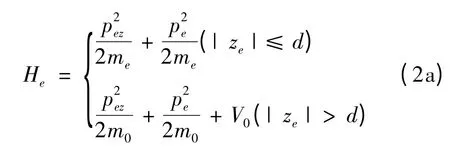
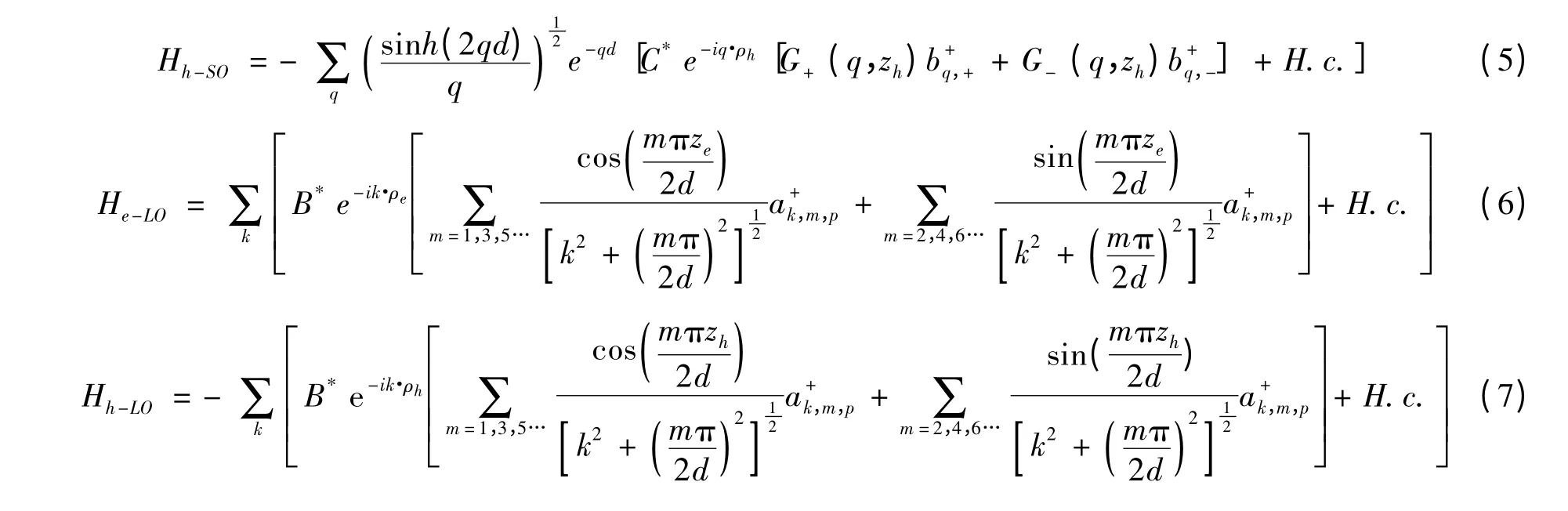
y引入激子的质心坐标和相对坐标［12］，对激子质心动量和坐标引进下列Huybrechts［13］线性组合算符，最后引入两次幺正变换算符［14］

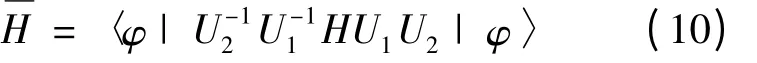
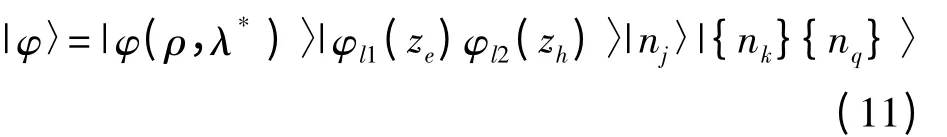
|φ〉是有限温度下的尝试波函数. 其中|φ(ρ，λ*)〉为二维激子内部运动的波函数; |φl1(ze)φl2(zh)〉为电子和空穴在z 方向移动的本征函数;|nj〉|{nk}{nq}〉分别为极化子态和声子态. 通过对和λ 变分可以得到激子声子系统的有效哈密顿量

F(λ，λ*)对λ 的变分得到参量λ0. 参量λmin可以通过(15)式解得，我们能得到等式λ*=λmin.

3 数值计算结果和讨论

为了更清楚地说明极化子效应和温度对极性晶体膜中强耦合激子性质的影响，以AgBr 晶体膜为例进行数值计算. 数值计算结果表示为图2 至图4.

图2 在N=10 时，激子与LO 声子相互作用所产生的诱生势Ve，h-LO与坐标ρ 和温度T 的关系曲线Fig.2 The relationships of the exciton induced potential Ve，h-LO，which is induced by the interaction between the exciton and LO-phonon，with the coordinate ρ and temperature T at N=10

图2 表示AgBr 极性晶体膜中激子与LO 声子相互作用所产生的诱生势Ve，h-LO在一定的膜厚度N=10 时和不同的温度T(=0K，50K，100K)与电子-空穴间距离ρ 的变化曲线. 从图2 可以看出，Ve，h-LO随ρ 的减小而增大，随温度T 升高而减小，温度T 的降低也增强了诱生势Ve，h-LO随电子-空穴间距离ρ 的减小而增大的程度.

图3 在T=50K 时，激子与LO 声子相互作用所产生的诱生势Ve，h-LO与坐标ρ 和N 的关系曲线Fig.3 The relationships of the exciton induced potential Ve，h-LO，which is induced by the interaction between the exciton and LO-phonon，with the coordinate ρ and N at T=50K

图3 表示AgBr 极性晶体膜中激子与LO 声子相互作用所产生的诱生势Ve，h-LO在一定的温度T=50K 时和不同的膜厚度N(=10，20，30)与电子-空穴间距离ρ 的变化曲线. 从图3 可以看出，Ve，h-LO随ρ 的减小而增大，随膜厚度N 增加而增大. 这是因为随着膜厚度的增加，激子与LO 声子相互作用增强，所以激子与LO 声子相互作用产生的诱生势逐渐增大.

图4 在T=50K 时，激子与SO 声子相互作用所产生的诱生势Ve，h-SO与坐标ρ 和N 的关系曲线Fig.4 The relationships of the exciton induced potential Ve，h-SO，which is induced by the interaction between the exciton and SO-phonon，with the coordinate ρ and N at T=50K

图4 表示AgBr 极性晶体膜中激子与SO 声子相互作用所产生的诱生势Ve，h-SO在一定的温度T=50K 时和不同的膜厚度N(=10，20，30)与电子-空穴间距离ρ 的变化曲线. 从图4 可以看出，Ve，h-SO随ρ 的增大而减小. 另外，由图4 也可以看出，诱生势Ve，h-SO随膜厚度N 减小而增大. 这是因为在极性晶体膜较薄时，激子与SO 声子的耦合较强，与体LO 声子的耦合较弱. 所以膜越薄，激子与SO 声子相互作用产生的诱生势Ve，h-SO越大.

4 结 论

过去研究强耦合极性晶体中极化子的方法十分复杂，当然，要进一步用于讨论强耦合激子将变得更复杂. 本文采用改进线性组合算符和LLP变分相结合的方法，便可以较容易得出极性晶体膜中强耦合激子的有效哈密顿量. 研究结果表明:极性膜中激子与不同支声子的耦合强烈程度是不同的. 在膜厚较薄时，激子与表面声子耦合较强;在极性膜较厚的情况下，激子与体纵光学声子的耦合是主要的，表面声子的作用就比较小了. 同时激子的诱生势不仅与电子空穴间距离有关，而且温度对诱生势的影响是不可忽略的.

［1］ Eerdunchaolu，Bai X F，Han C. Properties of the internal excited state of the strong-coupling magneto-bipolaron in a parabolic quantum dot［J］. Acta Phys.Sin.，2014，63(2):027501-1(in Chinese)［额尔敦朝鲁，白旭芳，韩超. 抛物量子点中强耦合磁双极化子内部激发态性质［J］. 物理学报，2014，63(2):027501-1］

［2］ Zhao C L，Wang L L，Zhao L L. The properties of ground state of polaron in quantum disk in finite depth potential well［J］. J. At. Mol. Phys.，2013，30(4):638(in Chinese)［赵翠兰，王丽丽，赵丽丽. 有限深势阱里量子盘中极化子的基态性质［J］. 原子与分子物理学报，2013，30(4):638］

［3］ Jiang F S，Zhao C L. Excitation energy and frequency of transition spectral line of electron in quantum ring［J］. RESEA RCH ＆ PROGRESS of SSE，2013，33(3):238(in Chinese)［姜福仕，赵翠兰. 量子环中电子的激发能量和跃迁谱线频率［J］. 固体电子学研究与进展，2013，33(3):238］

［4］ Wang T X，Xia Y B. Interface optical phonon modes and electron-phonon interactions in wurtzite GaN/ZnO quantum wells［J］. J. At. Mol. Phys.，2011，28(1):139(in Chinese)［王天兴，夏雅兵. 纤锌矿GaN/ZnO 量子阱中的界面声子及其电声相互作用［J］. 原子与分子物理学报，2011，28(1):139］

［5］ Ding Z H，Zhang J F. The properties of excited state of the weak coupling bound polaron in quantum wires［J］. RESEA RCH ＆ PROGRESS of SSE，2012，32(2):101(in Chinese)［丁朝华，张建芳. 量子线中弱耦合束缚极化子激发态的性质［J］. 固体电子学研究与进展，2012，32(2):101］

［6］ Wang X Q. Variation of the polaron average and cyclotron resonance frequency of the bound magnetopolaron in a polar slab［J］. J. At. Mol. Phys.，2012，29(3):507(in Chinese)［王秀清. 极性晶体膜中束缚磁极化子的声子平均数与回旋共振频率的关系［J］. 原子与分子物理学报，2012，29(3):507］

［7］ Hu W T，Yang H T，Ji W H，et al. The polaron effects and temperature dependence of the strong-coupling exciton in slab of polar crystals［J］. J. At. Mol.Phys.，2012，29(6):1114(in Chinese)［胡文弢，杨洪涛，冀文慧，等. 极性晶体膜中强耦合激子的极化子效应和温度依赖性［J］. 原子与分子物理学报，2012，29(6):1114］

［8］ Eerdunchaolu，Yu R M. Temperature dependence of quasi-two-dimensional strong-coupling exciton'effective mass［J］. Acta Optica Sinica，2009，29(4):1106(in Chinese)［额尔敦朝鲁，于若蒙. 准二维强耦合激子有效质量的温度依赖性［J］. 光学学报，2009，29(4):1106］

［9］ Shen M，Zhang L，Liu J J. The influence of magnetic field and the quantum dot size on the properties of exciton ［J］. Acta Physica Sinica，2012，61 (21):217103-1(in Chinese)［沈曼，张亮，刘建军. 磁场和量子点尺寸对激子性质的影响［J］. 物理学报，2012，61(21):217103-1］

［10］ Wang W J，Wang H L，Gong Q，et al. External electric field effect on exciton binding energy in InGaAsP/InP quantum wells［J］. Acta Physica Sinica，2013，62(23):237104-1(in Chinese)［王文娟，王海龙，龚谦，等. 外电场对InGaAsP/InP 量子阱内激子结合能的影响［J］. 物理学报，2013，62(23):237104-1］

［11］ Lei X L，Wang D W，Liang S X，et al. Wavefunction and Fourier coefficients of excitons in quantum wells:computation and application［J］. Acta Physica Sinica，2012，61(5):057803-1(in Chinese)［雷小丽，王大威，梁士雄，等. 半导体量子阱中激子波函数及其Fourier 系数的计算和应用［J］. 物理学报，2012，61(5):057803-1］

［12］ Gu S W，Meng Y S. Exciton in a slab of polar crystal［J］. Phys. Rev. B，1987，35(18):9817.

［13］ Huybrechts J. Note on the ground-state energy of the Feynman polaron［J］. J. Phys. C，1976，9:L211.

［14］ Eerdunchaolu，Xiao J L，Li S S. Effects of electron phonon coupling on the surface properties of the polaron in the CdF2semiconductor film［J］. Chinese Journal of Semiconductors，2000，21(3):225(in Chinese)［额尔敦朝鲁，肖景林，李树深. CdF2半导体膜中电子-表面声子强耦合对极化子性质的影响［J］. 半导体学报，2000，21(3):225］