单分子磁体中交换常数计算的新方法
胡耀乔,张召富,张 浩,周铁戈
(1. 南开大学电子信息与光学工程学院,天津300071;2. 西南财经大学统计学院,成都611130)
1 引 言
近年来,在单分子磁体(Single - Molecule Magnet,SMM)[1-5]的研究中,过渡金属多核配合物凭借独特的单分子磁体行为和量子效应,在电子输送、新型电子器件、量子计算和高密度信息存储器件等领域越来越受到人们的重视[6,7]. 在这些多核配合物中,以Fe 和Mn 这两种元素的化合物为典型代表[8]. 例如,Caneschi 等人[9]在1997年研究发现,含Mn 的簇合物,凭借具有大的表面/体积比例而引起特殊的尺寸效应或量子效应,在均相催化、光催化、光电子器件和生物体系中原子和电子输送等领域中都具有应用价值. 另外,单分子磁体还可以用于量子计算[10]、磁存储[11]、自旋阀[12]等.
交换常数可以反映磁耦合的强弱,从而可以确定是铁磁耦合或者是反铁磁耦合,交换耦合常数的计算是当前磁性研究的重要内容之一[13,14].确定单分子磁体中磁性原子之间交换常数也就具有重要的意义[15]. 在得到交换常数后,不但能确定分子基态自旋,还能指导新型单分子磁体的合成. 2009 年,Silvia 等人[16]计算了Fe9分子中的交换耦合常数,2004 年,Ruiz 等人[17]研究了Fe19分子中的交换耦合常数.
采用密度泛函理论(Density functional theory,DFT)[18,19]的方法可以较好计算单分子磁体原子之间磁交换耦合常数. Boullant 等人[20]和Benelli 等人[21]研究证实,基于密度泛函理论的方法计算的交换耦合常数和通过Monte -Carlo 模拟所获得的实验数据符合的很好. 尽管如此,这种计算方法目前来说还是比较繁琐的.
本文在密度泛函理论的基础上,提出了一个简单合理的计算方法来计算单分子磁体的交换常数,并对Fe7和Fe20配合物分子进行了研究. 本文介绍我们的研究方法和结果.
2 模型与计算方法
对于单分子磁体,磁性依赖于体系中存在的各种相互作用,不考虑零场分裂时,一般采用自旋哈密顿量(^H)来描述,表达式为
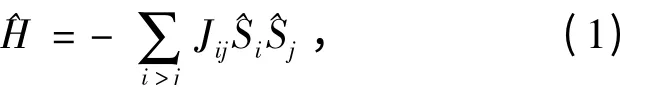
其中,^Si和^Sj分别表示i 和j 两个磁性中心的自旋算符,Jij即i 和j 两个磁性中心的各向同性交换偶合常数,它的符号的大小分别标志着交换耦合作用的性质(Jij>0 标志着铁磁相互作用;Jij<0 标志着反铁磁相互作用)和强弱.
计算交换耦合常数的一般方法是,如果一个单分子磁体中要计算n 个不同的交换耦合常数,则需要计算出n 种不同自旋分布组合情况下所对应的体系能量,从而可建立一个包含未知数交换耦合常数J 的含有n 个等式的方程组. 以文献[17]计算Fe19分子中各磁交换中心间的交换耦合常数为例,Fe19中有9 个不同交换耦合常数,因此需选取9 种不同的自旋分布组合来建立9 个方程,如其中的一种选取组合为Fe19中Fe3、Fe11、Fe13自旋向上,而其他有磁矩Fe 原子自旋向下. 可以看出,这种计算方法需要实现选择不同的自旋分布组合,而不同的选择可能导致不同的结果. 这种方法在原子数目较少时适宜,但当分子中具有磁矩的原子数目过多或者对称性过于复杂而难以分析清楚时这种方法就不可取了.
为克服上述方法带来的不便,本文中提出如下公式进行计算
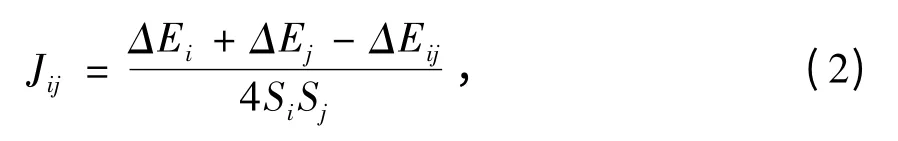

对于一个具有n 个磁矩原子的体系而言,其因交换耦合而具有的能量为
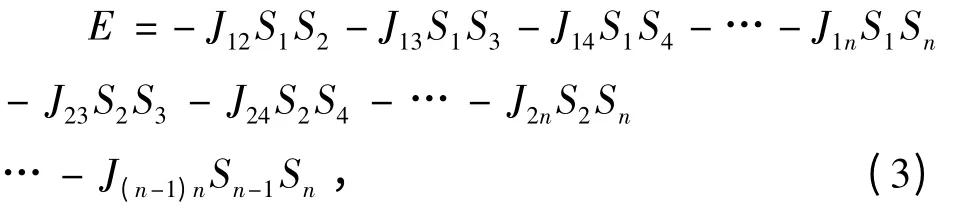
只考虑交换耦合常数Jij,上式可写为

由于自旋的方向性,在上式中以分别以Si= - Si,Sj= -Sj和Si= -Si,Sj= -Sj代入上式可得到下面三式

由此,得到

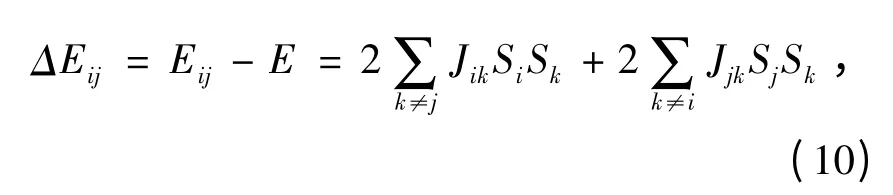
(8)式+(9)式-(10)式,有

即

这样,在计算某两个原子之间的交换耦合常数J 时,只需要设置这两个原子的自旋方向并计算出对应体系的能量就可以计算出两个原子之间的交换常数,避免了在传统方法中需要选取恰当的自旋分布组合.
采用以上方法,我们对Fe7分子[22]以及Fe20分子[23]的交换常数进行了计算. 利用基于密度泛函理论的第一性原理计算软件包SIESTA(Spanish Initiative for Electronic Simulations with Thousands of Atoms)[24,25]进行. SIESTA 中的基组是数值原子轨道的线性组合(Linear combination of atomic orbitals,LCAO),采用DZP(double-ζ basis plus polarization orbitals)展开价电子波函数. 采用Perdew,Burke 和Ernzerhof (PBE)[26]的 广 义 梯 度 近 似(GGA)描述电子间的交换关联作用. 计算中收敛标准设定为10-6eV,实空间网格截断能量(Mesh Cutoff)设定为240 Ry. 各原子的价电子组态分别为:H:1s1,C:2s22p2,O:2s22p4,Fe:3d64s2.
3 结果与讨论
Fe7分子的结构如图1 所示. Fe7中包含183个原子,其中Fe 原子有13 个,但只有7 个是有磁矩的,这7 个Fe 原子分为三类:Fe(I)(Fe7)、Fe(II)(Fe2,Fe4,Fe6)、Fe(III)(Fe1,Fe3,Fe10).因此Fe7分子中有四个不同的交换耦合常数J12、J17、J26、J27. 用这种计算方法求得的各个交换耦合常数见表1.从表1 中的计算结果可以看出,Fe7分子中各Fe原子间的交换耦合均为反铁磁耦合,这符合实验结果,并且Fe7分子中四类不同的交换耦合都属于较强的反铁磁耦合. 结果与Silvia[16]等人对Fe9分子的计算类似,交换耦合常数的正负性和数量级都没有明显差异.

图1 Fe7 中7 个具有磁性的铁原子的几何结构示意图Fig.1 Molecular structure of Fe7 complex
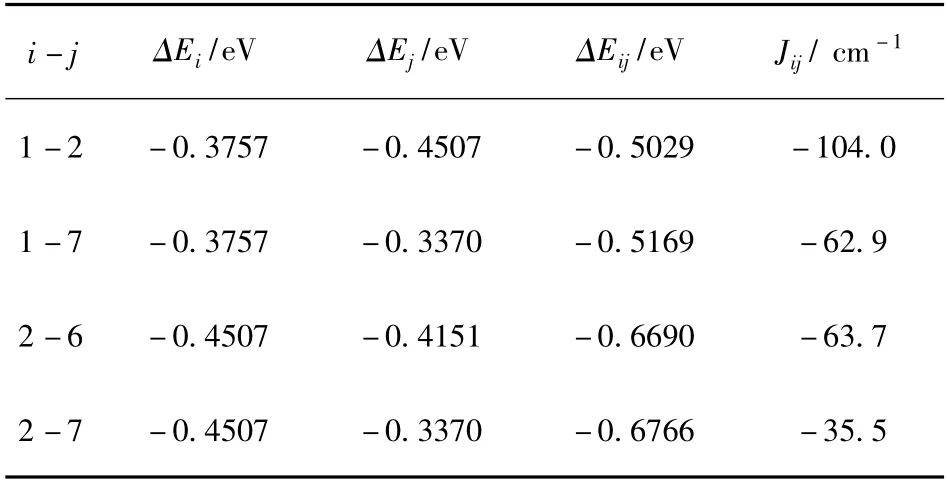
表1 Fe7 分子中各交换耦合常数计算结果Table 1 Calculation results of all the exchange coupling constants in Fe7
用这种方法还可以计算Fe20分子各Fe 原子间交换耦合常数,Fe20分子结构如图2 所示.

图2 Fe20中铁原子的几何结构示意图Fig.2 Molecular structure of Fe20 complex
Fe20分子中共包含206 个原子,其中Fe 原子20 个. 考虑到Fe20分子结构中Fe 原子分布的中心对称性,可以只关心右边一半Fe 原子间的交换耦合关系,这部分Fe 原子因交换耦合而一共有25个交换耦合常数. 采用该方法求解出来Fe20分子中各交换耦合常数计算结果见下表2.
从表2 中的计算结果可以看出,Fe20分子中各Fe 原子间的交换耦合均为反铁磁耦合,与类似分子的相关计算相符. Ruiz 等人[17]对Fe19分子的计算给出的交换耦合常数同样都为负,而且数量级相一致.

表2 Fe20分子中各交换耦合常数计算结果Table 2 Calculation results of all the exchange coupling constants in Fe20
4 结 语
采用基于密度泛函理论的计算方法,推导出了计算单分子磁体中不同磁性原子间的交换耦合常数的新方法,并计算出Fe7和Fe20配合物各交换耦合常数. 计算结果表明,Fe7和Fe20配合物中的交换耦合均为反铁磁耦合,其正负性以及数量级都与类似分子的相关研究一致. 研究表明,这种计算方法,可以有效地避免方程组法所带来交换耦合常数计算值不稳定的情况,也免去了分析分子中磁交换中心分布的对称性的麻烦,对于分析计算具有多个磁交换中心的单分子磁体的交换耦合常数特别适用.
[1] Caneschi A,Gatteschi D,Sessoli R,et al. Alternating current susceptibility,high field magnetization,and millimeter band EPR evidence for a ground S = 10 state in[Mn12O12(CH3COO)16(H20)4)]·2CH3COOH·4H2O[J].J. Am. Chem. Soc. ,1991,113:5873.
[2] Sessoli R,Tsai H L,Schake A R,et al. High -spin molecules:[Mn12Ol2(O2CR)16(H2O)4][J].J. Am.Chem. Soc.,1993,115(5):1804.
[3] van der Zant H S J. Single-molecule magnets:Reading a nuclear spin with electrons [J]. Nat. Nano.,2010,7:555.
[4] Hang W,Chang S Q,Dai Y D,et al. Magnetism and mossbauer spectra of cyanide-bridged Ni-Fe nanomolecular- magnets [J]. Chin. Phys. Sin.,2008,57(04):2493(in Chinese)[韩薇,常树全,戴耀东,等. 氰根桥联Ni(II)-Fe(III)类纳米分子磁体磁性及穆斯堡尔谱研究[J]. 物理学报,2008,57(04):2493]
[5] Gatteschi D,Sessoli R. Quantum tunneling of magnetization and related phenomena in molecular materials[J]. Angew. Chem. Int. Ed.,2003,42:268.
[6] Wang T W,Lin X J,Wei J Z,et al.Single-molecular magnets [J]. Chin. Inorg. Chem.,2002,11(18):1071 (in Chinese)[王天维,林小驹,韦吉宗,等. 单分子磁体[J]. 无机化学学报,2002,11(18):1071]
[7] Ritter S K. Single - molecular magnets evolve [J].Chem. Eng. News.,2004,82(50):29.
[8] Grapperhaus C A,O’Toole M G,Mashuta M S. Synthesis and structure of the tetradeca -iron(III)oxide– alkoxide cluster [Bu4N]2[Fe14O8(OCH2CH3)20Cl8][J]. Inorg. Chem.Commun.,2006,9:1204.
[9] Caneschi A,Gatteschi D,Sessoli R. Manganese clusters:a common ground for photosynthesis,quantum tunnelling of the magnetization and colossal magnetoresistance[J]. J. Chem. Soc. Dalton Trans.,1997,3963.
[10] Leuenberger M N,Loss D. Quantum computing in molecularmagnets[J]. Nature,2001,410:789.
[11] Mannini M,Pineider F,Sainctavit P,et al. Magnetic memory of asingle-molecule quantum magnet wired to a gold surface[J]. Nature Materials,2009,8:194.
[12] Urdampilleta M,Klyatskaya S,Cleuziou J P,et al.Supramolecular spin valves[J]. Nature Materials,2001,10:502.
[13] Hao Y M.A calculation of the exchange interaction constant between the R-sublattice and the 3d -sublattice in R2Fe17-xAlxcompounds[J].Acta Phys. Sin.,2000,49 (11):2287(in Chinese)[郝延明. R2Fe17-xAlx化合物中R-T 交换耦合常量的计算[J]. 物理学报,2000,49(11):2287]
[14] Liu W,Liu X H,Cui W B,et al. Exchange couplings in magnetic films[J].Chin. Phys. B,2013,22 (2):027104.
[15] Indranil R,Qin W,Troy V V. Accurate magnetic exchange couplings in transition - metal complexes from constrained density-functional theory[J]. J. Chem.Phys.,2006,124:024103.
[16] Go'mez-Coca S,Ruiz E,Kortus J.Single-molecule magnet Fe9supramolecular dimers:a theoretical approach to intramolecular and intermolecular exchange interactionsw[J]. Chem. Commun.,2009,4363.
[17] Ruiz E,Rodríguez-Fortea A,Cano J,et al. Theoretical study of exchange coupling constants in a Fe9complex[J].J. Phys. Chem. Solids.,2004,65:799.
[18] Hohenberg P,Kohn W. Inhomogeneous electron gas[J]. Phys. Rev.,1964,136:B864.
[19] Zhou G P,Wang Y B.DFT theoretical study on intermolecular interactions of H4P2O7with H2O[J]. J. At.Mol. Phys.,2012,29 (1):22(in Chinese)[周国萍,王一波. DFT 理论研究焦磷酸与水的分子间相互作用[J]. 原子与分子物理学报,2012,29(1):22][20] Boullant E,Cano J,Journaux Y,et al. The utilization of classical spin Monte Carlo methods to simulate the magnetic behavior of xtended three-dimensional cubic networks incorporating M (II)ions with an S = 5/2 ground state spin[J]. Inorg. Chem.,2001,40:3900.
[21] Benelli C,Cano J,Journaux Y,et al. A decanuclear iron (III)single molecule magnet:use of Monte Carlo methodology to model the magnetic properties[J]. Inorg. Chem.,2001,40:188.
[22] Masello A,Sanakis Y,Boudalis A. K,et al. Iron(III)chemistry with ferrocene - 1,10 - dicarboxylic acid (fdcH2):an Fe7cluster with an oxidized fdcligand[J]. Inorg. Chem.,2011,50:5646.
[23] Zeng Y F,Hu X,Xue L,et al. Fe20cluster units based coordination polymer from in situ ligand conversion and trapping of an intermediate [J]. Inorg.Chem.,2012,51:9571.
[24] Soler J M,Artacho E,Gale J D,et al. The SIESTA method for ab initio order - N materials simulation[J]. J. Phys.:Condens. Matt.,2002,14:2745.
[25] Cheng Z D,Ling T,Zhu J. First-principles calculation of magnetism of icosahedral Fe clusters[J]. Chin.Phys. B,2010,19:057101.
[26] Perdew J P,Burke K,Ernzerhof M. Generalized gradient approximation made simple [J]. Phys. Rev.Lett.,1996,77:386.

