一类非线性信号去噪的奇异值分解有效迭代方法

查 翔倪世宏 张 鹏

(空军工程大学航空航天工程学院 西安 710038)

一类非线性信号去噪的奇异值分解有效迭代方法

查 翔*倪世宏 张 鹏

(空军工程大学航空航天工程学院 西安 710038)

对于一类非线性信号的去噪问题，该文提出一种基于奇异值分解(Singular Value Decomposition, SVD)的有效迭代方法。对现有奇异值差分谱方法在两类不同非线性信号上的去噪效果进行了对比，指出在信号不具有明显特征频率、非周期性变化时这一方法并不适用，并分析了现象产生的原因；然后针对该类信号的特点重新定义了Hankel矩阵结构，给出有效奇异值的确定方式，并通过SVD多次迭代过程实现对该类信号的有效去噪。对实际飞行数据去噪的实验结果表明，该方法对提出的一类信号对象不仅去噪效果良好，而且可提高运算效率。

信号处理；去噪；奇异值分解；特征频率； Hankel矩阵

1 引言

在工程测试中受系统本身和环境干扰的影响，现场采集的机械设备状态信号往往含有各种噪声，若能及时有效地将噪声从有用信号中消除，还原设备运行的真实状态，对于进一步的信号分析处理以及设备状态监控、故障诊断等具有重要意义。

当前业界流行的去噪方法主要涉及非线性滤波[1]、小波阈值法[2−4]以及奇异值分解(Singular Value Decomposition, SVD)[5]等。非线性滤波去噪效果的优劣取决于滤波器结构是否设计合理，而且过程存在一定的时间延迟。小波阈值法过度依赖小波阈值以及分解层数的选择，不同选择方式下的去噪效果存在较大差异。SVD去噪的实质是线性加权式的正交化分解，得到的去噪信号不存在相位偏移和时间延迟，在1维振动信号[6]以及2维图像去噪[7]、时间序列预测[8]中得到广泛应用。

基于SVD的去噪方法主要解决两个方面的问题：Hankel矩阵结构的确定以及有效奇异值的选择。对Hankel矩阵结构的确定问题常被忽略，由于无有效理论依据，对其奇异值分解前的结构一般凭经验事先确定[9]。另一个关键问题是有效奇异值的选择，SVD的基本思想就是通过有效奇异值对矩阵重构，从而实现信号去噪的目的，通常用信噪比经验值的估计选择有效奇异值的阈值[10,11]，但在工程中难以实现。文献[12]提出一种非常有代表性的方法：基于奇异值差分谱理论的SVD去噪，根据差分谱的最大峰值确定有效奇异值的个数，从而实现有效奇异值的自适应选择。然而，对于一类无明显特征频率，不具有明显周期性特点的信号而言，采用以上矩阵结构方式以及有效奇异值的选择方法均不能有效实现信号去噪。主要表现在去噪后的信号只能描述出原始信号的大尺度变化趋势，细节信息丢失过多，以致引起波形失真。文献[13]所针对的具有明显变化趋势的信号对象亦可划为这一类信号的范畴。

本文提出一种针对一类非线性信号去噪的奇异值分解有效迭代方法，处理后的信号与原始目标波形非常接近，细节特征基本被完好保留，能够实现信号的有效去噪。

2 基于SVD的去噪原理

设1维离散信号x={x(i)}, i=1,2,…,N。为利用SVD对该信号进行去噪处理，首先要对其进行相空间重构，采用滑动窗口依次截取的方式获得多个行向量，从而构造出Hankel矩阵：其中n为滑动窗口的宽度，且1＜n＜N。若令m= N−n+1，则A∈Rm×n。对A作奇异值分解，即必存在正交矩阵U∈Rm×m和正交矩阵V∈Rn×n，使得

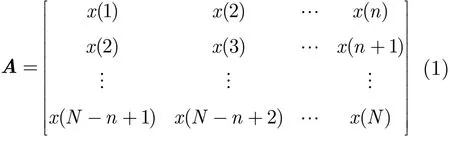
其中对角阵Σ∈Rm×n, Σ中的各对角线元素σ1, σ2,…,σq称为A的奇异值，q=min(m,n)≥2，并满足σ1≥σ2≥…≥σq＞0，实际中常取m≥n。x对应的Hankel矩阵中任意两行完全不相关，为满秩矩阵，并且奇异值序列具有的特点为

式(3)中的“≫”表示前k个奇异值远大于之后的q−k个奇异值，在第k个与第k+1个奇异值之间存在较明显的跳变。由于每个奇异值对应着一个分量信号，前k个奇异值代表着有用信号，而后q−k个奇异值则对应着噪声。因此，可以选择前k个奇异值作为有效奇异值，而将其它剩余奇异值置0，就可以依据Frobenius范数意义下的矩阵最佳逼近定理实现逆过程运算，以得到重构后的去噪信号。

信号去噪效果的优劣与有效奇异值的选取有关。现有基于奇异值差分谱的选取方法可较好描述奇异值序列的突变规律[12]，差分谱的定义为

其中k=1,2,…,q −1，则序列c=(c1,c2,…,cq−1)构成了奇异值差分谱，若相邻两奇异值差值较大，则必会在差分谱序列中产生一个最大峰值，其对应式(3)中的突变位置k，从而实现有效奇异值的自适应选择。

Hankel矩阵的不同结构直接影响到q的取值以及去噪效果。文献[14]指出Hankel矩阵在最为接近方阵即q值最大时，滤波效果最好，具体结构为

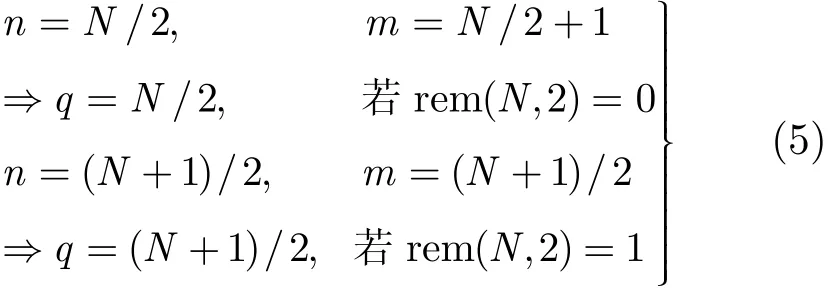
其中rem(⋅,⋅)表示取余运算，这也是基于奇异值差分谱的SVD方法常采用的形式。

3 基于SVD的一类非线性信号去噪特点描述

以式(5)所示的Hankel矩阵结构为前提，基于奇异值差分谱的SVD去噪方法对于一类具有特殊属性的非线性信号而言并不适用。为更好地说明问题，首先设计一个仿真信号x(t)=sin(4t)+sin(8t)，在t∈[0,2π]区间内共采样512个点，同时加入信噪比约为2.24的白噪声，将奇异值序列以及奇异值差分谱同时置于图1(a)中(为能清楚显示只绘出了前50个点)。可以看到，奇异值序列的前4个值相对较大，在第5个位置处序列出现陡降；奇异值差分谱的最大峰值位于第4个坐标，k应取为4。按照差分谱选择奇异值的原则，取前4个奇异值重构后的信号如图1(b)所示。对比去噪前后的信号，奇异值差分谱方法有效去除了噪声，波形足够平滑，并且能反映出x(t)的构造特点，即由两个不同特征频率的周期正弦信号叠加组成，且仍为周期信号。图2给出了x(t)经快速傅里叶变换得到的幅值谱，虽然存在噪声频率的干扰，但仍可发现大约在0.79 Hz f=以及f=1.57 Hz 处存在明显的两个尖峰，这反映了信号的两个主特征频率，也是信号能量的主要分布频率。

然而，实际中的信号并不一定具有特征频率或周期特性，此时奇异值差分谱方法的去噪效果可能很差。以典型的Block信号为例(如图3(a)所示)，按式(5)对其构造Hankel矩阵并进行奇异值分解，得到奇异值与奇异值差分谱序列，取前50个位置点的结果如图3(b)所示。可以看到，奇异值差分谱的最大峰值位于第1个位置，说明原始信号包含较强的直流成分，此时应以第2大峰值位置确定k，易知k=3。选择前3个奇异值进行重构，恢复出的信号如图3(c)所示。不难看出，按奇异值差分谱方法得到的去噪信号丢失了大部分的波形细节，信号被过度平滑且出现波形失真，仅反映出大时间尺度上的整体趋势。

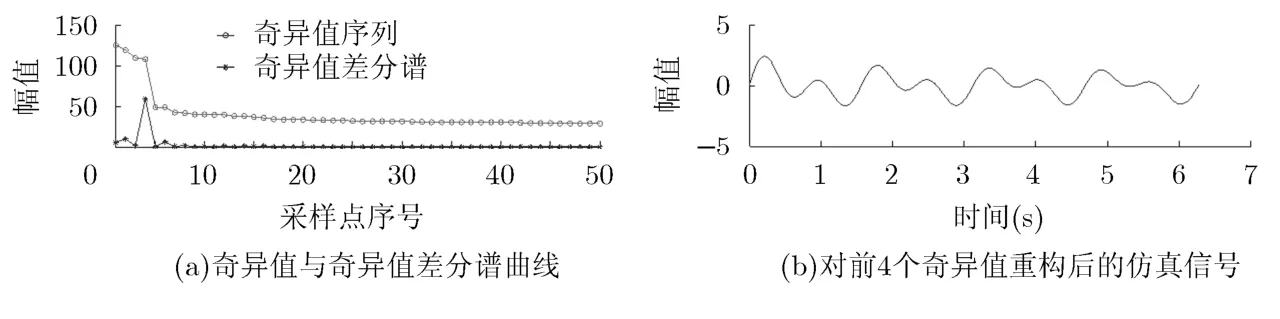
图1 仿真信号波形及SVD处理结果

图2 仿真信号的幅值谱

图3 Block信号波形及SVD处理结果

观察仿真信号与Block信号的时域波形，虽然混有一定程度的噪声，但仍能看出仿真信号带有明显的周期性，而Block信号却不具有这一特征，主体变化不存在明显规律，带有较强的随意性。为使结论更可靠，从频域角度分析两种信号的频率分布情况，给出Block信号的幅值谱如图4所示。根据噪声能量的分布特点，Block信号中的噪声在整个频域内分布较为均匀，而有用成分主要集中在低频段，说明Block信号除噪声外主要为低频的直流成分，但与文献[14]讨论的直流成分有明显区别。后者研究对象为直流、交流和噪声3种成分叠加在一起的的混合信号，其所指的直流成分是相对于交流而言的，实际为带有偏置特征的常数。从这个意义上来说，之前所设计的仿真信号可看作是由交流和噪声成分组成的混合信号。为与文献[14]中常数直流对象以示区别，本文将Block信号中这种低频直流成分称为广义直流成分，其显著特点是变化相对平缓，带有一定的随机性，并且无明显周期规律。

4 针对一类非线性信号的SVD有效迭代去噪

4.1 方法引入

通过对比两类信号的去噪效果可知，实际中一类无代表性特征频率的含噪信号主要包含了广义直流成分与噪声，对于这类信号，基于奇异值差分谱的SVD方法无法实现有效去噪。具体原因可从以下两个方面分析：

(1)Hankel矩阵结构的合理性 一般认为，奇异值数量q越大，奇异值序列的分布规律会更加明显，如此才会在保留基本波形的前提下拥有最大的噪声去除量，这一结论在信号仅含有交流和噪声成分，或同时含有直流、交流和噪声3种成分时的去噪效果是十分显著的，而对仅含有广义直流和噪声成分的信号则不然。可以推断，不论原始信号中是否含有直流成分，交流成分与噪声成分之间的分布差异需要较多的奇异值来体现，以实现两种成分的分离；而对于仅含有广义直流和噪声成分的无代表性特征频率的信号而言，这种对奇异值较多数量的要求未必适用。

文献[12]推导出直流分量的能量仅由第1个奇异值所代表；若信号中同时存在交流分量，其能量则由第2个奇异值起的有限个奇异值所代表。虽然本文定义的广义直流分量不一定为常数，但与噪声能量的分布特性相比，能量仍然较为集中。由于本文的研究对象不存在明显的交流成分，可以推断，过大的q将导致广义直流分量能量的分散，即有一部分能量可能散失至噪声对应的奇异值中，在进行有效奇异值筛选的同时也将这部分能量进行了去除，从而丢失了部分细节。为使这种能量损失降到最低，并能同时完成去噪的目标， q应尽可能取小，同时考虑到Hankel矩阵本身的定义要求，n只能设置为2，且由m与n之间的约束关系，m应取为N−1。

(2)有效奇异值数量 k的选择 奇异值差分谱方法虽然在有效奇异值与其它奇异值之间进行了隔断，但不能保证有用分量与噪声之间的精确分离，有效奇异值的过多或过少均会影响去噪效果。根据图1(a)，第1大峰值与第2大峰值之间的差距很大，使得噪声能被有效去除。作为对比，Block信号奇异值差分谱的两最大峰值分别位于第3和第5个坐标(见图3(b))，两峰值之间的差距远不如仿真信号的明显，并且之后还连续有一些差距不大的峰值出现，而这些峰值携带了有用信号的某些细节信息。通过一系列实验可以发现，若以其它峰值的位置为基准对Block信号继续增加奇异值，发现去噪后的波形细节虽有一定程度的增加，但同时也会引入部分噪声。根据这一分析，基于奇异值差分谱的SVD方法在面对一类无代表性特征频率的含噪信号时，难以取得理想的去噪效果。

考虑到矩阵结构被重新定义，k也需重新选择，但必须受q的约束，即k＜q。根据对Hankel矩阵结构合理性的讨论以及q=min(m,n)可知，k仅能取1。

以上分析过程完成了对SVD去噪方法中相关参数的重新定义，仍以Block信号为例，观察进行1次SVD去噪的效果(见图5(a))。可以判定，相对于图3(a)中的原始信号，进行1次去噪处理后的信号去除了部分噪声，同时保留了大部分有用细节，说明重新定义的相关参数对提升Block信号的去噪效果具有一定作用。还需注意到，仅进行此处理过程还无法达到去噪所要求的理想波形，但不可否认的是，这一处理方式是有效的，关键在于如何进一步处理，以去除剩余噪声。为此，自然联想到继续迭代处理的方式，即对前一次处理得到的信号再次按照重新定义的相关参数进行处理。为验证这一思路的合理性，图5(b)给出了重复迭代3次处理后的信号波形，与图5(a)的波形相比，显然更多的噪声被去除，波形曲线也更为平滑，同时也保证了细节信息的保留。

4.2 方法的流程描述

基于以上分析，本文提出一种SVD迭代处理的去噪方法，具体步骤为：

步骤 1 对长度为N的目标信号x构造Hankel矩阵，其中设置矩阵列数n=2，则行数m=N−1；

步骤2 确定迭代次数T，并令当前迭代次数i=1；

步骤 3 对Hankel矩阵进行奇异值分解，选择第1个奇异值为有效奇异值(因为k=1)，同时将其它奇异值置0，然后按平均法进行信号重构[15]，得到初次处理的去噪信号x'；

步骤 4 若i＜T，说明当前结果信号未达到结束条件，i=i+1，并将x'作为下次处理的目标信号，x'→x，返回步骤3，否则输出x'作为最终的去噪信号。

一个需要解决的问题是如何确定迭代次数T，对不同信号进行迭代处理的结果表明，只需较少的迭代次数就会达到令人满意的效果，此时噪声去除量已趋近饱和，若继续迭代，信号波形的变化将十分微小。从这一意义上来说，迭代次数的选择具有较强的灵活性，可根据实际去噪效果进行合理选取。

4.3 时间复杂度分析

步骤1需要对信号序列以滑动窗口的方式依次截取m次，时间复杂度为O(m)；对于步骤2～步骤3，若矩阵维数为m×n，则分解与重构过程的时间复杂度分别为O(4m2n+8mn2+9n3), O(mn)；对于步骤4，每次迭代时信号长度均为N, Hankel矩阵维数也一致，故每次迭代所用时间复杂度相同。假若共进行T次迭代，则整个过程所用时间复杂度为(O(m) +O(4m2n+8mn2+9n3)+O(mn))×T≈O(Tm2n)。按本文方法n被设置为2, m=n或仅相差1。一般而言，信号长度N通常会很大，考虑到m+n=N+1为常数，根据数学常识，当m与n差距很小时两者之积要远大于差距很大时的两者之积，并且由于T非常小，本文方法的复杂度要远小奇异值差分谱方法。

5 实例验证与分析

反映军用飞机发动机状态的飞行数据是一种典型的非平稳、非线性信号，受各种内外部因素的影响，飞行数据中将不可避免地会混入各种噪声。图6(a)给出了某型飞机在处于飞行状态时采集到的一段真实振动值Vib信号，从波形上看不具有明显的周期性。求解它的幅值谱观察整个频带区间内的频率分布(见图6(b))，发现能量主要集中在低频段，不存在明显尖峰，故符合本文研究对象的特点。

Vib原始采样信号的长度N=1200，按照本文所提出的方法，首先构造Hankel矩阵，其列数n=2，行数m=1199；取不同的试验迭代次数T=5和T=50。对构造好的Hankel矩阵作奇异值分解，并选择第1个奇异值为有效奇异值，同时将其它奇异值置0，然后重构信号，不同迭代次数下的去噪结果如图7。

从图7可以看出，本文方法对于不规律变化的Vib信号去噪效果较好，在经过5次迭代后的去噪波形已十分理想，信号较为纯净，不带有明显的噪声；同时波形细节也非常丰富，在整个时间范围内可明显分辨信号的变化趋势，能够满足振动值状态监控的实际需求。另外，当迭代50次后，相对于图7(a), Vib信号的波形改变量极其微小，只表现在某些细节处，因而继续迭代已无必要。在实际应用中，迭代次数的选择不宜过多，应该根据实际信号的变化特点合理选择迭代次数，提高处理效率。

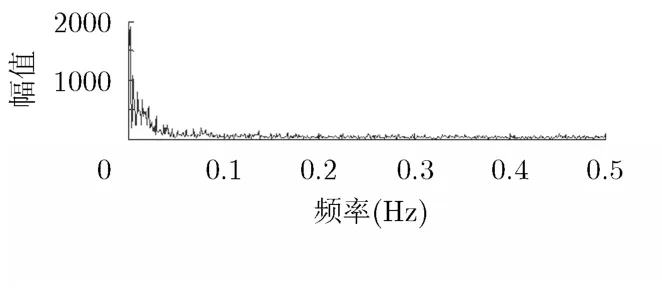
图4 Block信号的幅值谱

图5 不同SVD处理次数的结果对比

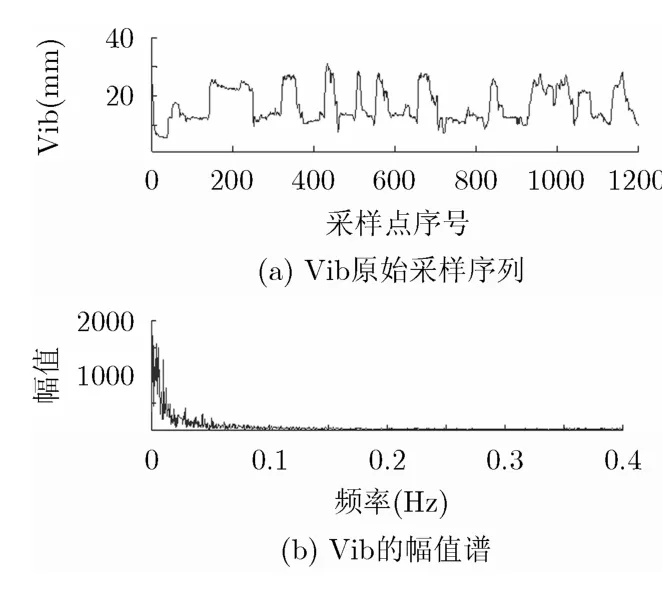
图6 Vib原始采样信号及幅值谱

图7 不同迭代次数下Vib信号的去噪效果对比

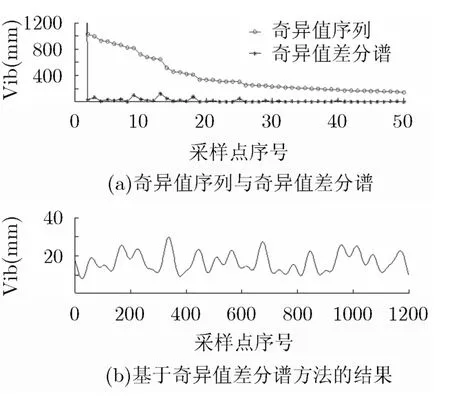
图8 基于奇异值差分谱方法的Vib 序列处理结果及去噪波形

为体现本文方法在去噪上的优势，对Vib信号采用基于奇异值差分谱的SVD方法进行去噪实验，得到奇异值序列以及奇异值差分谱如图8(a)所示。由于第1个奇异值较大，为清晰显示其它较小的奇异值，图中并未将第1个奇异值绘出。可以看到，差分谱序列的第1大峰值位于第1个坐标处，按照差分谱方法的选择原理，应以第2大峰值位置为准选择有效奇异值，即k=13。选择前13个奇异值作为有效奇异值进行信号重构，得到的结果如图8(b)所示，与图7相比，虽然奇异值差分谱方法绘出了Vib信号大致的变化趋势，但仍存在有用细节丢失的现象。例如在150～230以及950～1050采样点区间内，信号被过度平滑，从而引起波形失真。

计算时间方面的结果如表1所示。可以看出，本文方法在取得较好去噪效果的同时(即T=5)，所耗费时间要远小于基于奇异值差分谱方法，而且当T=50时，所耗费时间才与基于奇异值差分谱方法相近，这一结论也印证了4.3节对时间复杂度分析的正确性。这同时也从另一个侧面说明，过多的迭代次数并不能保证去噪质量的大幅度提升，反而会降低本文方法在时间效率上的优势。通过以上实验结果表明，无论从去噪效果还是计算效率来看，本文方法均要优于基于奇异值差分谱的方法。

6 结束语

对于一类非线性含噪信号，本文提出了一种迭代处理的有效去噪方法。首先为Hankel矩阵设置有效维数，对其进行奇异值分解后确定有效奇异值数目，然后完成信号的重构。若未达到迭代次数，对获得的新信号重复上述过程，最终获得理想的去噪信号。在真实飞行数据上的实验结果显示出本文方法只需较少的迭代次数即可达到理想去噪效果，运算时间也得到有效缩减，能够满足应用需求。

表1 不同方法的运行时间比较

[1] Massari C, Brocca L, Ciabatta L, et al.. A Wiener-wavelet based filter for de-noising satellite soil moisture retrievals[C]. Proceedings of the EGU General Assembly, Vienna, Austria, 2014: 1123-1148.

[2] Donoho D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(2): 613-618.

[3] He Wang-peng, Zi Yan-yang, Chen Bin-qiang, et al.. Tunable Q-factor wavelet transform denoising with neighboring coefficients and its application to rotating machinery fault diagnosis[J]. SCIENCE CHINA Technological Sciences, 2013, 56(8): 1956-1965.

[4] Maryam A and Rodrigo Q Q. Automatic denoising of single-trial evoked potentials[J]. NeuroImage, 2013, 66(10): 672-680.

[5] Pascal P M, Christian B, and Florence B. Denoising NMR time-domain signal by singular-value decomposition accelerated by graphics processing unites[J]. Solid State Nuclear Magnetic Resonance, 2014, 61(5): 28-34.

[6] Li Zhen-xing and Dai Wei-xiao. Local mean decomposition combined with SVD and application in telemetry vibration signal processing[J]. Applied Mechanics and Materials, 2013,347(2): 854-858.

[7] Ajit R, Anand R, and Arunava B. Image denoising using the higher order singular value decomposition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(4): 849-862.

[8] Cheng D H, Xu Q J, and Yao W F. Regional wind energy resource forecasting based on SVD and support vector machine[J]. Advanced Materials Research, 2014, 247(12): 1070-1072.

[9] 赵学智, 叶邦彦, 陈统坚. 奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J]. 机械工程学报, 2010, 46(1): 100-108.

Zhao Xue-zhi, Ye Bang-yan, and Chen Tong-jian. Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe[J]. Journal of Mechanical Engineering, 2010, 46(1): 100-108.

[10] 吕永乐, 郎荣玲. 基于奇异值分解的飞行数据降噪方法[J]. 计算机工程, 2010, 36(3): 260-262.

Lü Yong-le and Lang Rong-ling. Noise reduction method for flight data based on singular value decomposition[J]. Computer Engineering, 2010, 36(3): 260-262.

[11] Zhao H M, Shen H, Fu Y, et al.. Using singular value decomposition and high order spectrum for bearings fault diagnosis[C]. Proceedings of the IEEE Transportation Electrification Conference and Expo Asia-Pacific(ITEC Asia-Pacific), Beijing, China, 2014: 1-4.

[12] Zhao Xue-zhi and Ye Bang-yan. Selection of effective singular values using difference spectrum and its application to fault diagnosis of headstock[J]. Mechanical Systems and Signal Processing, 2011, 25(5): 1617-1631.

[13] 雷达, 钟诗胜. 基于奇异值分解和经验模态分解的航空发动机健康信号降噪[J]. 吉林大学学报, 2013, 43(3): 764-770.

Lei Da and Zhong Shi-sheng. Aircraft engine health signal denoising based on singular value decomposition and empirical mode decomposition methods[J]. Journal of Jilin University, 2013, 43(3): 764-770.

[14] 赵学智, 叶邦彦, 陈统坚. 基于小波-奇异值分解差分谱的弱故障特征提取方法[J]. 机械工程学报, 2012, 48(7): 37-48.

Zhao Xue-zhi, Ye Bang-yan, and Chen Tong-jian. Extraction method of faint fault feature based on wavelet-SVD difference spectrum[J]. Journal of Mechanical Engineering, 2012, 48(7): 37-48.

[15] Brand M. Incremental singular value decomposition of uncertain data with missing values[C]. Proceeding of the 2002 European Conference on Computer Vision, Copenhagen, Denmark, 2002: 1-12.

查 翔： 男，1988年生，博士生，研究方向为飞机状态监控与故障诊断、人工智能及其应用等.

倪世宏： 男，1963年生，教授，博士生导师，研究方向为飞行数据智能处理、飞行器状态监控与健康管理等.

张 鹏： 男，1982年生，博士，讲师，研究方向为航空发动机故障诊断、故障预测与健康管理等.

Effective Iteration Method of a Class of Nonlinear Signal Denoising Based on Singular Value Decomposition

Zha Xiang Ni Shi-hong Zhang Peng
(College of Aeronautics and Astronautics Engineering, Air Force Engineering University, Xi'an 710038, China)

To solve a class of nonlinear signal denoising, an effective iteration method based on the Singular Value Decomposition (SVD) is proposed. When the signals have no obvious characteristic frequency and non-periodic change, the current difference spectrum method is not applicable by comparing the results on the two class of nonlinear signal, and then the corresponding reason is analyzed. According to the signal feature, the structure of the Hankel matrix is defined again and the valid singular values are determined. The effective denoising is realized by the repeated iteration which is based on the SVD. The results of the flight data demonstrate that the proposed method can effectively reduce the noise and improve the computing efficiency as well.

Signal processing; Denoising; Singular Value Decomposition (SVD); Characteristic frequency; Hankel matrix

TN911.7

： A

：1009-5896(2015)06-1330-06

10.11999/JEIT141605

2014-12-15收到，2015-03-05改回

国家自然科学基金(61372167, 61379104)资助课题

*通信作者：查翔 zha_xiang@126.com