局部有界函数的Integral型Lupas-Bézier算子的收敛阶

局部有界函数的Integral型Lupas-Bézier算子的收敛阶

黄东兰1,2

（1.泉州师范学院数学与计算机科学学院；2.智能计算与信息处理福建省高等学校重点实验室，福建泉州362000）

对局部有界函数f的Integral型Lupas-Bézier算子在区间[0,¥)上收敛于的收敛阶进行研究，利用Cauch-Schwarz不等式和Lupas基函数的概率性质等方法，对前人关于Integral型Lupas-Bézier算子收敛阶的系数估计作了进一步的改进，得到了较优的系数估计。

局部有界函数；Lupas-Bézier算子；收敛阶

引言

Bézier型算子在逼近论有着重要的理论价值，在计算机辅助几何造型设计等领域有着广泛的应用价值。因而Bézier型算子成为研究热点，受到众多学者的重视。近年来关于Bézier型算子的研究成果丰硕[1-7]，其中Zeng[1]和黄坤阳[2]等研究了局部有界函数f的概率型算子Integral型Lupas-Bézier算子收敛于的收敛阶的估计。本文中将进一步讨论关于Integral型Lupas-Bézier算子收敛阶，利用Cauch-Schwarz不等式和Lupas基函数的概率性质等方法进行计算和推导，得到了更优的估计式。本文首先介绍Integral型Lupas-Bézier算子。

1定义和引理

定义1设f是定义在区间[0,)¥上的可测函数，称下列为Integral型Lupas-Bézier算子：

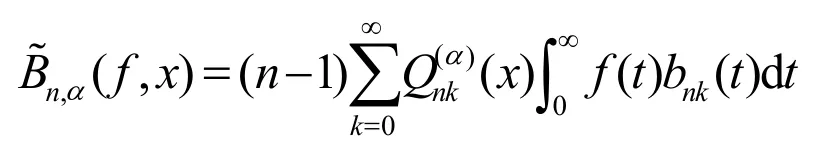
（1）

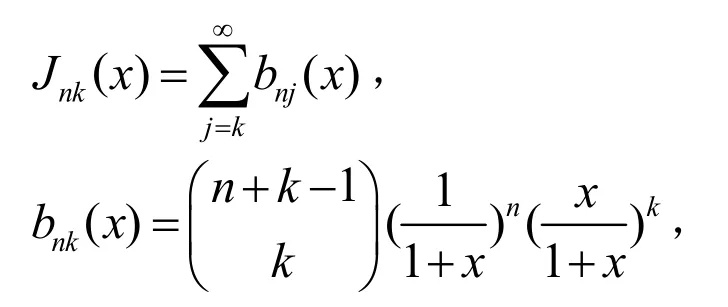
k=0,1,2,L。

定义2对于I上的有界函数，称函数

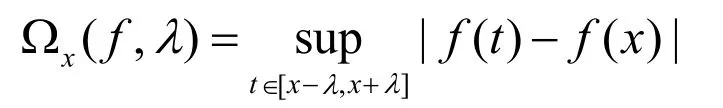
为度量函数。其中,x是(,)-¥+¥上的定数，l³0。

为了得到本文的结果，我们引入一些引理。

引理1[8]设为独立同分布的随机变量序列，数学期望,方差，三阶绝对矩，标准正态分布又设)，对于所有的n=1,2,L,则

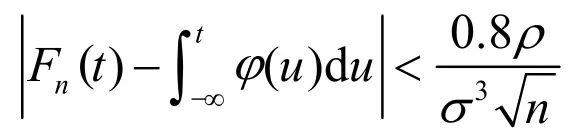
（2）

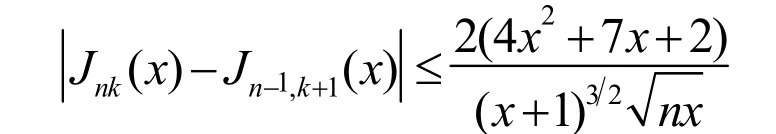
（3）

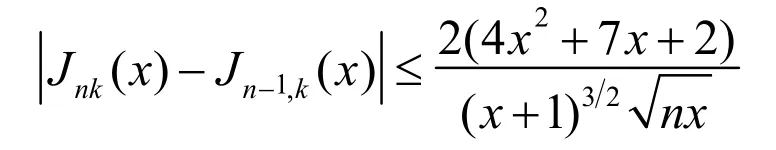
（4）

证明：设(0,)

（5）

则x的方差和四阶中心矩依次为

（6）

（7）

由式（6）和式（7），根据Cauch-Schwarz不等式得

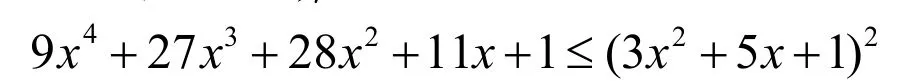
即

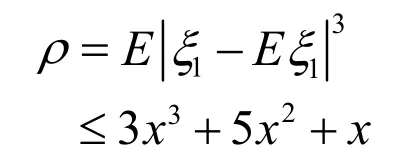
（8）

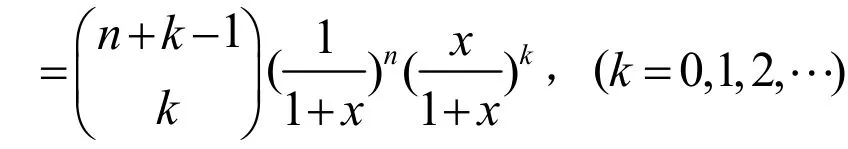
（9）

对nh作标准化变换，则由式（2）及式（8）得

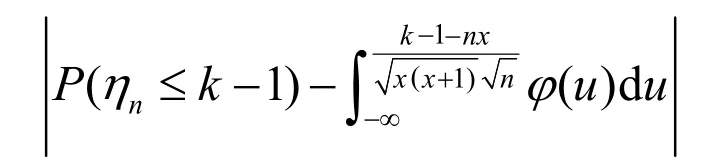
（10）

（11）

又在文献[1]对引理4的证明过程中已经得出不等式：

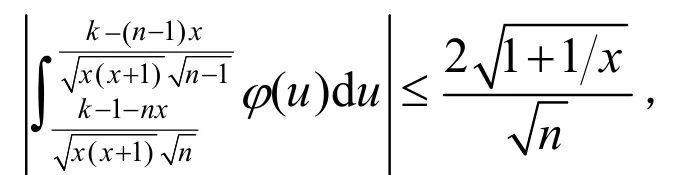
即

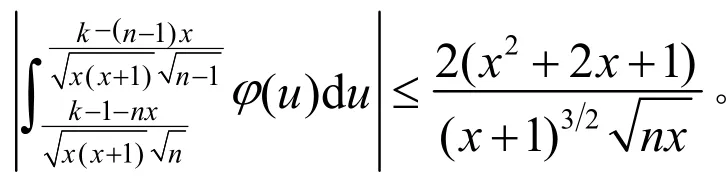
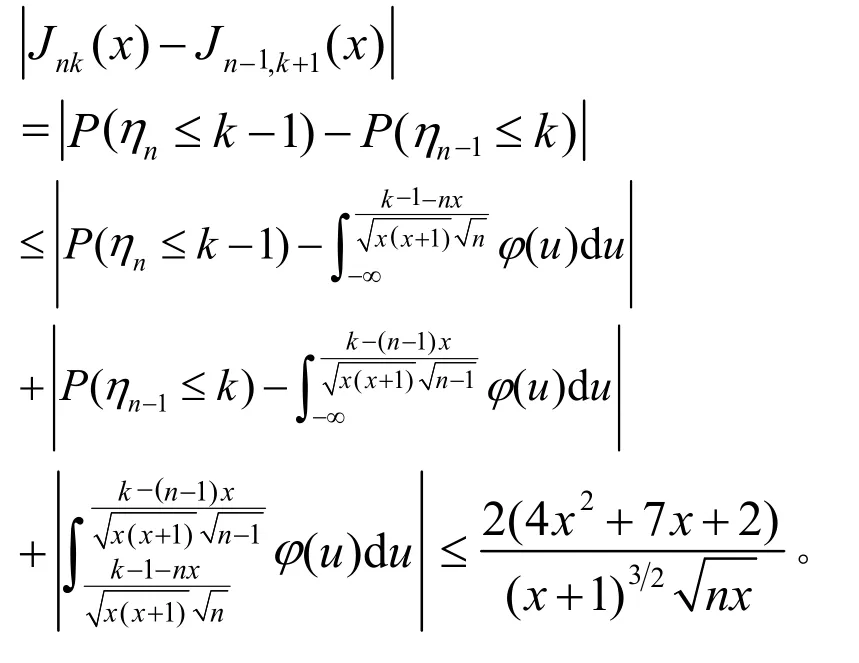
则式（3）成立；同理可得式（4），引理2得证。

2主要结果

有

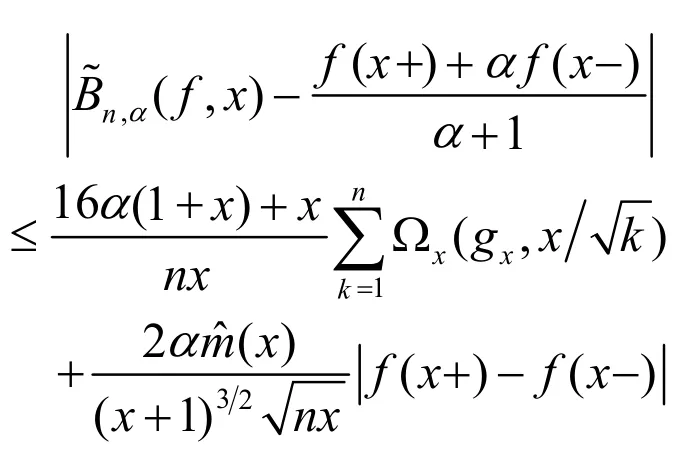
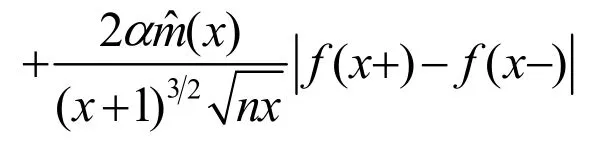
（13）

证明：注意到对所有的t

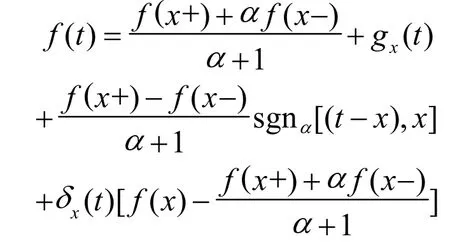
14

其中：

又

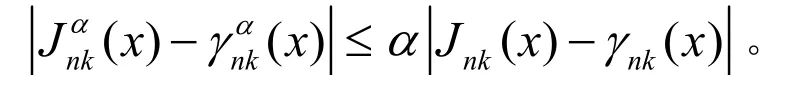
由引理2得

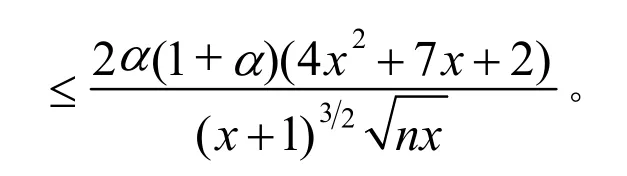
（16）

另一方面黄坤阳[2]已经有

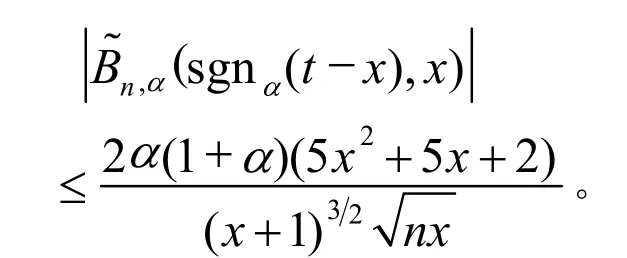
（17）

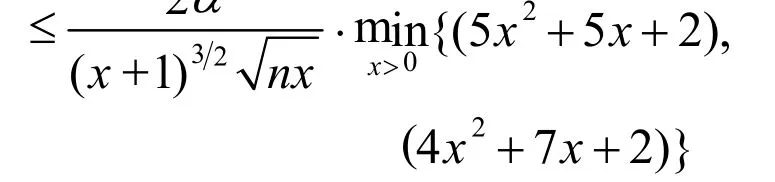
即

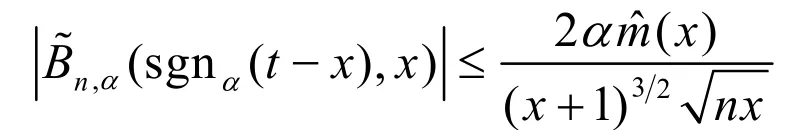
（18）

其次对于式（15）中，Zeng[1]在其定理的证明过程中对已经得到了如下估计式：

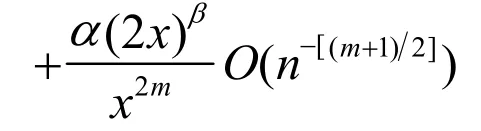
（19）

把式（18）、（19）代入式（15）得式（13），定理1得证。

结束语

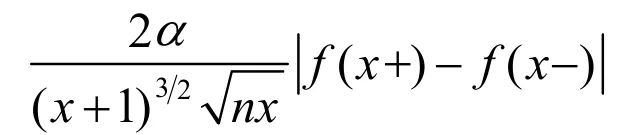
对于定理1中式（13）右端第二项的系数，Zeng[1]和黄坤阳[2]研究得出的估计依次为

（20）

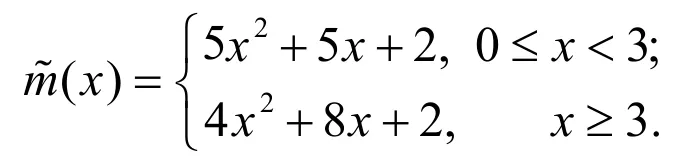
（21）

把本文所得的系数估计和Zeng[1]和黄坤阳[2]所得的计算结果进行比较,显然，特别的，当3x>时，。从而，对于估计式（13）右端第二项的系数估计而言，本文的系数估计较优。

[1] Zeng X. M. ，Wang T. Rate of convergence of the integral type Lupas- Bézier operators[J]. Kyungpook Mathematical Journal， 2003，43(4)：593-604.

[2] 黄坤阳．Integral型Lupas-Bézier算子收敛阶的估计[J]. 巢湖学院学报,2015，17(3)：12-15.

[3] 黄东兰，王平华. Durrmeyer-Bézier算子收敛阶的新估计[J].泉州师范学院学报,2014,32(6):86-88.

[4] 黄东兰．局部有界函数的Baskakov-Bézier算子收敛阶新的估计[J]．三明学院学报, 2014, 32(6)：11-14.

[5] 杨军，曾晓明. 关于广义Durrmeyer- Bézier算子的Lp逼近[J].厦门大学学报:自然科学版，2004，43(6)：753-756.

[6] Zeng X. M. ,Yang J.,Zuo S.L..Approximation of Pointwise of Szasz-Bezier type operators for bounded functions[J].International Journal of Mathematics game theory and algebra，2003,13(2)：191-197.

[7] 王绍钦，陈玲菊.Bernstein-Bezier-Kantorovich算子列的逼近阶估计[J].太原师范学院学报:自然科学版,2005， 4(2)：4-7.

[8] B.M.佐洛塔廖夫.独立随机变量和的现代理论[M].陈宗询,译.福州：福建科学技术出版社,1996：211-236.

(责任编辑：任锁全)

Rate of Convergence of the Integral Type Lupas-Bézier Operators for Locally Bounded Functions

HUANG Dong-lan1，2

(1.School of Mathematics and Computer Science, Quanzhou Nomal University 2.Fujian Provincial Key Laboratory of Data Intensive Computing，Quanzhou Fujian 362000)

In this paper, using Cauch-Schwarz inequality and the probabilistic property of Lupas primary operator，we study the rate of convergence of Integral type Lupas-Bézier operator which is convergent to [f(x+)+αf(x-)]/( α+1) on [0,∞) for the locally bounded function.f. Our study improves Zeng and the other scholars′ estimation of Integral type Lupas-Bézier operator. At the same time, we get more perfect estimates of coefficient.

the locally bounded function ; Lupas-Bézier operator；rate of convergence

O174.41

A

1009-2080（2015）06-0077-03

2015-10-20

福建省中青年教师教育科研项目（JA14262）。

黄东兰（1976-），女，福建泉州人，泉州师范学院讲师，硕士。