电磁场中电势的辨析
丁蕾
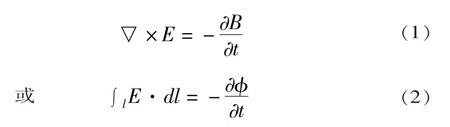
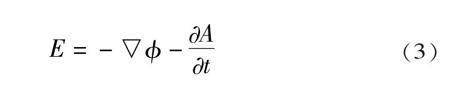
摘要:场是物理学科教学中电磁学部分的重要概念,而势是场量求解过程中常用到的“辅助”物理量。在职业学校的物理教学中,学生熟悉的都是静电场,对既有纵场也有横场的情况感到难以理解。所以对电动势和电势这两个常见的概念进行辨析,将有助于学生强化电磁场的概念。
关键词:电磁场;电动势;电势
中图分类号:G712 文献标志码:A 文章编号:1673-9094-(2015)12C-0025-03
电场强度E与磁感应强度B是求解电磁场的最终目标,但在求解的过程中,往往会根据具体情况引入标势或矢势。在职业学校的物理教学中,一般只涉及在静电场的情况下引入电标势,简称为电势。但是教材同时也要求学生了解变化的磁场产生的涡旋电场。虽然对于电磁感应,教学重点内容是磁通量,但是从理解电磁场本质的角度来看,即理解麦克斯韦的电磁理论[1]:变化的磁场产生电场,变化的电场产生磁场,还是很有必要对静电场与涡旋电场同时存在时的势进行讨论。
对于静电场与涡旋场同时存在时是否可以使用电势这个概念问题,目前有两种观点。[2]其一是电势是无旋有源的静电场中的概念,它不能被“引申”到无源有旋的涡旋场中去。其二是可以引进电势的概念。因为在环路中存在电流时,从全电路来看电场的安培环路定理依然成立,所以可以使用电势的概念。为了准确回答这个问题,我们必须先要厘清相关概念。
一、静电场和感生电场的区别与联系
从这两种电场的产生来分析,静电场中电荷密度不随时间变化而变化,所以在理论上讨论静电场时都是分析相对于观察者静止的电荷产生的场。故而静电场往往又称为库仑场,它与磁场的存在没有必然的关系。在实验中,描绘静电场的等势面或线时,往往用稳恒电流场来模拟静电场。比如在平面上将直流电的正极设置在圆平面的圆心处,负极设置为以R为半径的环形电极,如此等势面便为以正极为圆心的一系列同心圆。虽然等势面与处于圆心处的静止电荷产生的场一致,但不同的是此时必定存在稳恒的磁场。
涡旋电场是由变化的磁场产生的,它的强弱由磁场随时间的变化率决定。即
(1)
或(2)
从电与磁的对称角度来看,变化的磁场能产生电场,变化的电场必定能对产生磁场做出贡献。在高中阶段一般只介绍稳恒电流产生的磁场,其实电场变化产生的磁场即是通过引入麦克思韦位移电流来体现的。虽然不必要求学生了解麦克思韦位移电流与磁场强度之间的定量关系,但是这种电与磁的对称关系是有必要了解的,因为它涉及我们常说的物理图像或物理思想。
从它们对放入其中的电荷的作用来分析,不论是静电场还是涡旋场,放入的电荷都会受到电场力的作用,力的大小与电荷的量与场强都成正比,且正电荷受力的方向与场强方向一致。但通常将静电场对电荷的作用称为静电力,而将涡旋电场对电荷的作用力归属为非静电力的一种。在静电场中沿任意一个回路移动电荷,电场力做功为零,且在静电场中任意两点间移动电荷,电场力做功与移动的路径无关,只与电荷在电场中的初末位置有关,即电荷在场中的能量只与电荷在电场中的位置有关。与重力场相似,静电场是有源无旋的保守力场,故可以引入电势的概念来描述静电场的各种性质。而涡旋电场的电场线是闭合的,它是无源有旋场。在涡旋电场中,电荷沿闭合回路移动一圈,涡旋电场对电荷做的功不为零,所以涡旋电场对电荷的作用力不是保守力,引入电标势的概念是不适合的。事实上,在电磁学理论中,对于这种情况是用电标势与磁矢势一起来表达电场强度的,即
(3)
二、电路分析中的电动势与电势
上文用电磁场来分析和理解电势,但是教材的习题或试题多是以电路的形式出现。虽然我们知道用电磁场的方法来分析电路与传统的宏观电路分析方法本质上是一致的,特别是在处理主频电路时,必须使用场的分析方法,但在职业学校的物理教学中,学生还无法达到这一认识层次,所以电动势的概念显得尤为重要。
教材中明确指出:把单位正电荷从负极通过电源内部移到正极时,非静电力所做的功,就是电源的电动势。而感生电动势是由非静电力移动电荷做功而产生的,这里的非静电力就是电荷在涡旋电场中受到的电场力。因为当我们讨论确定的电路时,即是已经知道了确切的路径,所以在分析电路时,如果存在涡旋场,则在电路中应等价引入一个或多个“电源”。这样感生电动势或电源是在导体中维持某种电荷(或电流)分布的必要条件,可以看作是电路的电源部分,因而在外电路中,电势、电势差和电压等与没有涡旋场存在时便一致,分析电路中的电势高低或差值便可以应用含源的欧姆定律了。
三、涉及涡旋场的高考题分析
如上所分析的存在涡旋电场的电路问题,通常考察感应电动势大小、电场中任一点的场强大小,以及涡旋电场做功的多少。这三类问题都可以用(2)式来进行分析。求感应电动势大小的试题,对(2)式中环路积分可以用微元法,由于高中阶段的学生没有学过积分,所以需要定量计算的试题通常给出的是环状回路。因为涡旋电场的方向与环路的切线方向总是一致的,所以(2)式左边即是涡旋电场强度E乘以环路的周长,而利用(2)式右边磁通量的变化率可求电动势大小,然后除以环路的长度即可得到场强。
如2012年福建高考理科综合试题[3][4],这道试题的重点就在如何求出电场强度来。通过磁感应强度随时间变化的关系图可以看出,磁感应强度只是在一段时间内线性增加。在这一段时间内,环形导轨中存在涡旋电场,利用(2)式就可以计算得其大小。而涡旋场做功的大小可以用功能原理,也可以用电场力做功的公式求出,但此时考察的重点已经发生了变化。
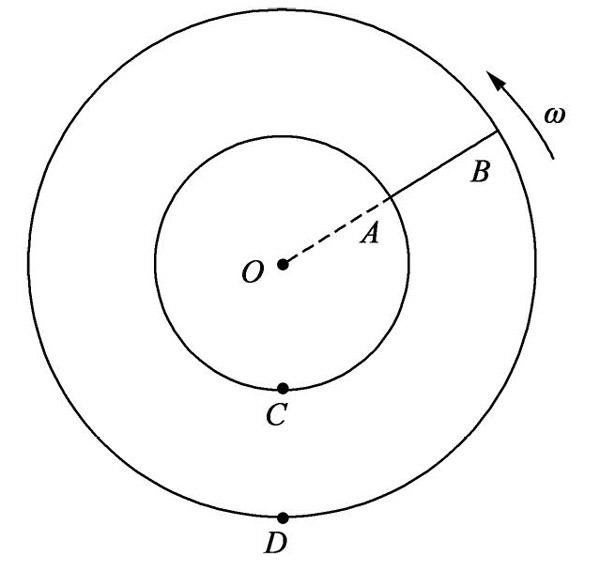
再如2011年浙江物理高考题,也是给出了磁感应强度随着时间变化的关系图,可以根据其线性变化关系,用(2)式求出感应电动势的大小。但值得注意的是,(2)式虽然可以由(1)式两边取面积分推得,但(2)式在使用的时候,右边的磁通量变化率未必是磁感应强暴随时间变化而产生的。如新课标2014年的高考题:半径分别为r和2r的同心圆形导轨固定在同一水平面内,一长为r、质量为m且质量分布均匀的直导体棒AB置于圆导轨上面,BA的延长线通过圆导轨中心O,装置的俯视图如图所示。整个装置位于一匀强磁场中,磁感应强度的大小为B,方向竖直向下。在内圆导轨的C点和外圆导轨的D点之间接有一阻值为R的电阻(图中未画出)。直导体棒在水平外力作用下以角速度ω绕O逆时针匀速转动,在转动过程中始终与导轨保持良好接触。高导体棒与导轨之间的动摩擦因数为μ,导体棒和导轨的电阻均可忽略。策略加速度大小g。求通过电阻R的感应电流的方向和大小;外力的功率。
此题在求解过程中必须求出电动势的大小,但此时显然是动生电动势,因为磁感应强度B并不随时间变化。但磁通量却是一直在变化,故而AB与CD间的阻,以及导轨构成的回路面积在随时间变化,所以仍然可以使用(2)式进行求解。
综上所述,涉及非静电场时,电标势的概念只对库仑场有意义,而对涡旋场是没有意义的。在讨论电路问题时,将感应电动势看作是电路中的电源,便可以应用含源电路的欧姆定律,如静电场问题一样来讨论电势、电势差和电压了。
参考文献:
[1]郭硕鸿.电动力学[M].北京:高等教育出版社,2008.
[2]沈志斌.关于涡旋电场的电势问题[J].物理教师,1990(4).
[3]徐慧.谈谈2012年高考中涡旋电场问题[J].中学物理,2013(31).
[4]王添华.涡旋电场中电势高低如何判断[J].物理教师,2014(35).
(责任编辑:冯志军)
Discrimination of Electric Potential in Electromagnetic Field
DING Lei
(Xuzhou Education Bureau, Xuzhou 221000, Jiangsu Province)
Abstract: Field is an important concept in electromagnetics in Physics teaching, while potential is commonly used in field solving process as an auxiliary physical quantity. In the Physics teaching in vocational schools, the students are familiar with the electrostatic field, but they have difficulty in understanding the situation with both longitudinal field and the transverse field. Therefore, the discrimination of electromotive force and electric potential will help to strengthen the students' understanding of the electromagnetic field.
Key words: electromagnetic field; electromotive force; electric potential
