基于PlD方法的控制力矩陀螺控制器设计

王佳伟,杨亚非,钱玉恒

(哈尔滨工业大学飞行器控制实验教学中心,黑龙江哈尔滨 150001)

基于PlD方法的控制力矩陀螺控制器设计

王佳伟,杨亚非,钱玉恒

(哈尔滨工业大学飞行器控制实验教学中心,黑龙江哈尔滨 150001)

控制力矩陀螺是一种常用的航天器的执行机构,广泛应用于卫星、空间站中。首先介绍了Model750型控制力矩陀螺结构组成,然后对该装置的数学模型进行了推导,并以Model750型控制力矩陀螺为研究对象,为其设计了PID控制器,并且设计了控制器参数、进行仿真验证,得到的仿真图形说明了控制力矩陀螺的控制性能良好。

控制力矩陀螺;控制器设计;PID

控制力矩陀螺作为执行机构常用于航天器姿态控制系统中[1-3],像国际空间站这样大型的航天器需要若干个单框架陀螺或双框架陀螺,通过一定的构型配置协同动作来完成姿态控制功能[4-12]。姿态控制的基本原理是通过改变高速旋转的陀螺飞轮转轴方向,使控制力矩陀螺产生角动量交换,从而改变角速度及姿态。目前,从微小卫星到大型的国际空间站,有近400多个航天器都采用控制力矩陀螺作为其姿态控制系统的主要执行器。我国近年发射的天宫一号飞船是国内第一次使用控制力矩陀螺作为执行机构的航天器。为了更好地掌握这类设备的性能,本文以美国ECP公司生产的Model750型的控制力矩陀螺实验装置为研究对象,介绍控制力矩陀螺的结构,推导其数学模型,进而基于PID方法为其设计控制器,来验证其运动性能。

1 控制力矩陀螺结构组成

该控制力矩陀螺由图1所示的3个部分组成。

第一个部分是控制力矩陀螺的机电部分,如图2所示。机电部分主体是由4个部件组成:框架A、B、C和转子D。转子D为大惯量铜转子,由稀土永磁型的直流伺服电机1提供输入转矩,使其绕轴1旋转,角位置由编码器1测量;框架C由直流电机2输入控制力矩,再由绞盘皮带放大转矩,驱动框架C绕轴2旋转,角位置由编码器2测量反馈;框架B相对于框架A绕轴3旋转,不对其施加主动转矩,角位置由编码器3测量;框架A相对于基座绕轴4旋转,不对其施加主动转矩,角位置由编码器4测量。此外,框架A、B、C还配置了摩擦滑环、惯性开关和制动器(框架C的制动器为虚拟制动,由执行软件设置)。

第二个部分是由M56000系列的DSP控制器板卡和输入输出电箱组成的控制系统,如图3所示。DSP控制器能够以高采样率执行控制律,解释轨迹命令,并支持数据采集、轨迹生成、系统状态及安全检测等功能。板卡中还包括可以实现编码器脉冲解码的逻辑门阵列和2个进行实时模拟信号测量的辅助数模转换器(DAC)。控制器的板卡与实际工业控制中使用的板卡相同。电箱主要功能是为机械部提供驱动电压,接收编码器的反馈信号,返回到控制器的板卡上。

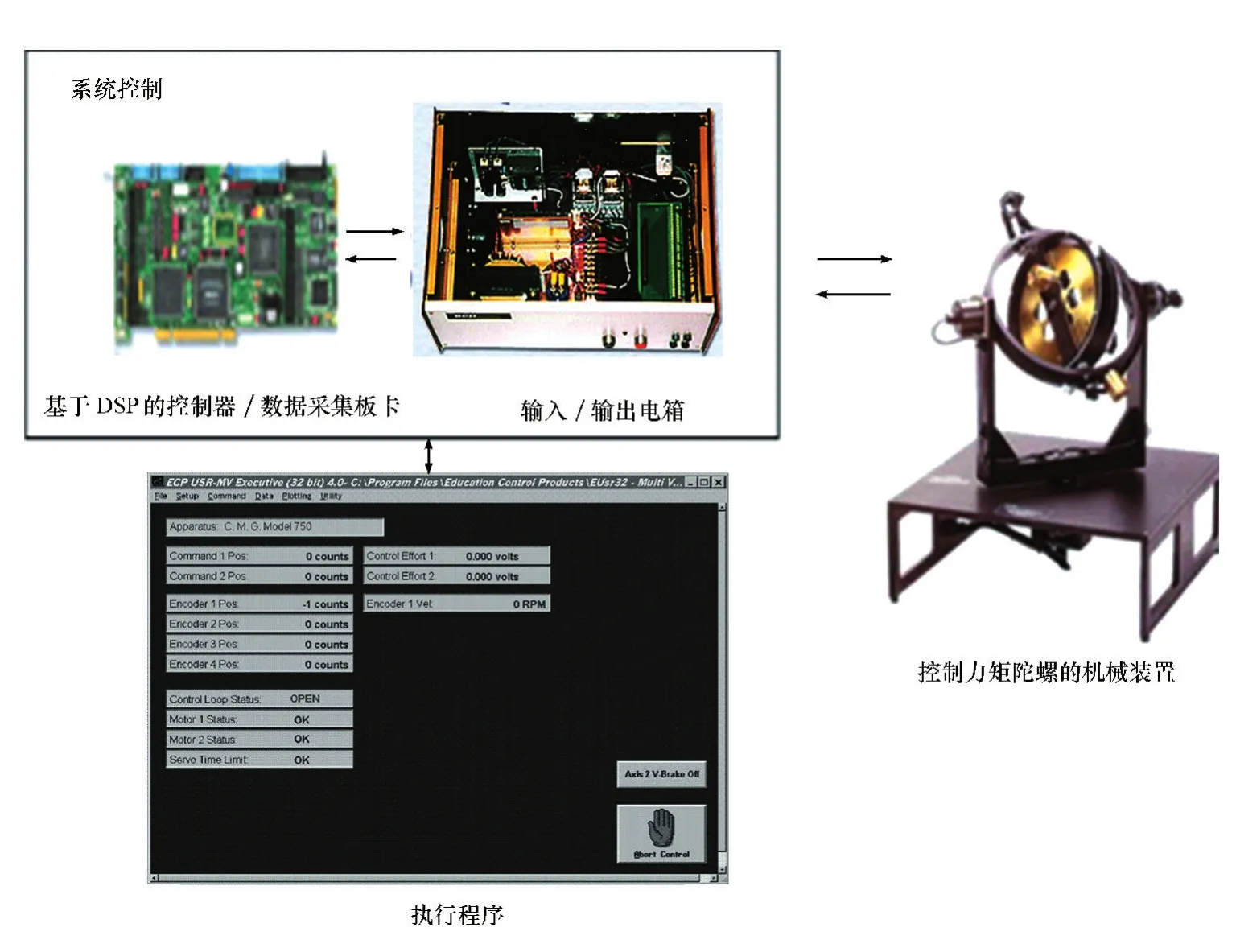
图1 控制力矩陀螺组成图

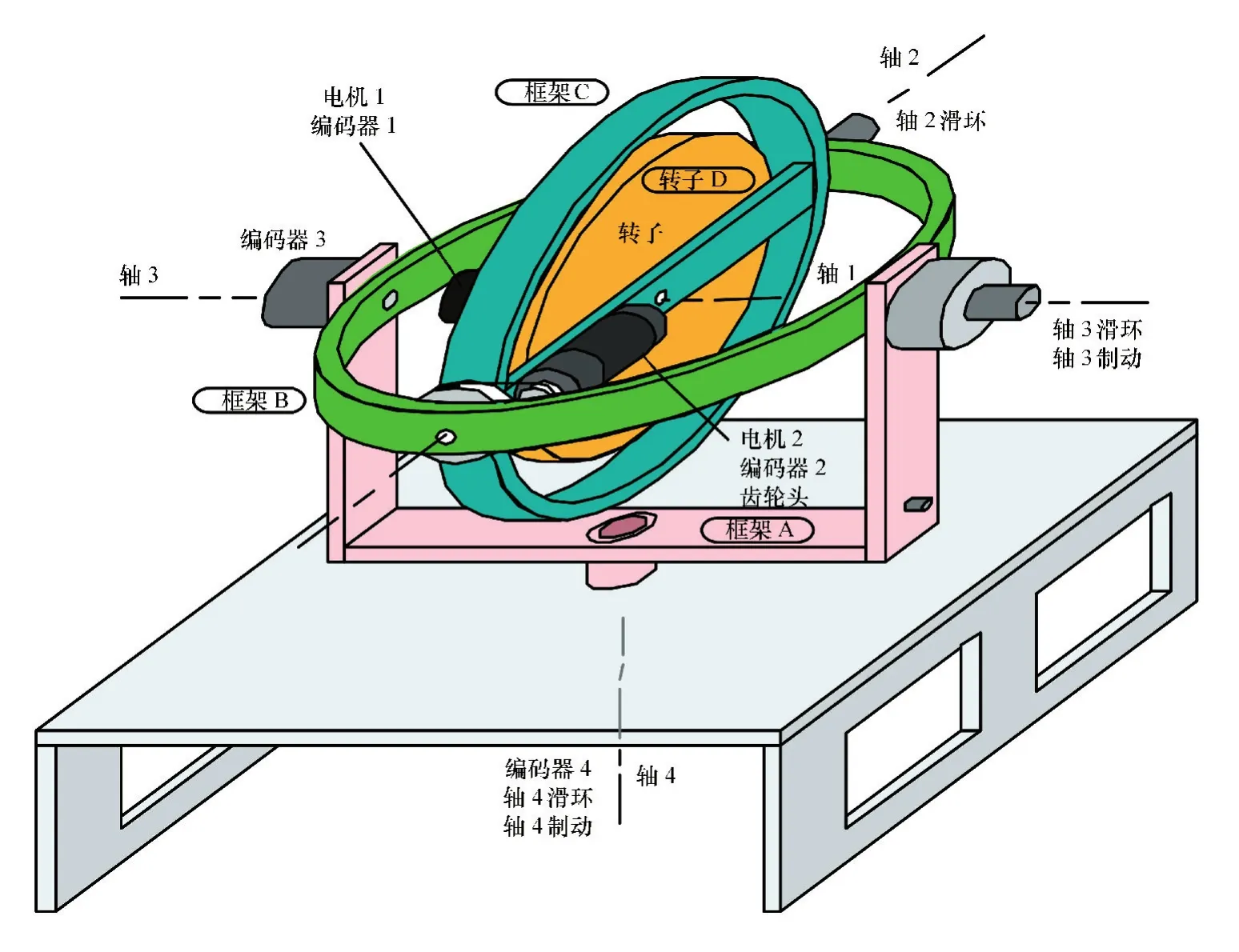
图2 机电部分

图3 控制系统部分

第三个部分是系统的执行程序,即用户界面、支持控制器算法编辑、输入信号设置、编码器数据采集和显示、绘图等功能。支持用户使用“类C”语言来编写控制器算法程序,可将其加载到基于DSP的实时控制板卡上,DSP在每个指定的采样周期执行此算法,读取参考输入和反馈传感器的值,经过计算将数字控制信号输出到数模转换器(DAC),数模转换器将数字流转换为一个模拟电压,然后通过一个伺服放大器转换为电流,再通过电机变为转矩,根据设备动力学特性将电机的输入转变为所期望的输出。当设备完成指定的动作后,传感器的测试数据通过电箱回传到执行软件中,用于绘图和存储。执行程序的运行窗口如图4所示。

图4 执行程序运行窗口

2 数学模型推导

首先需要建立一组坐标系,包括4个固连坐标系和1个惯性参考坐标系,如图5所示。

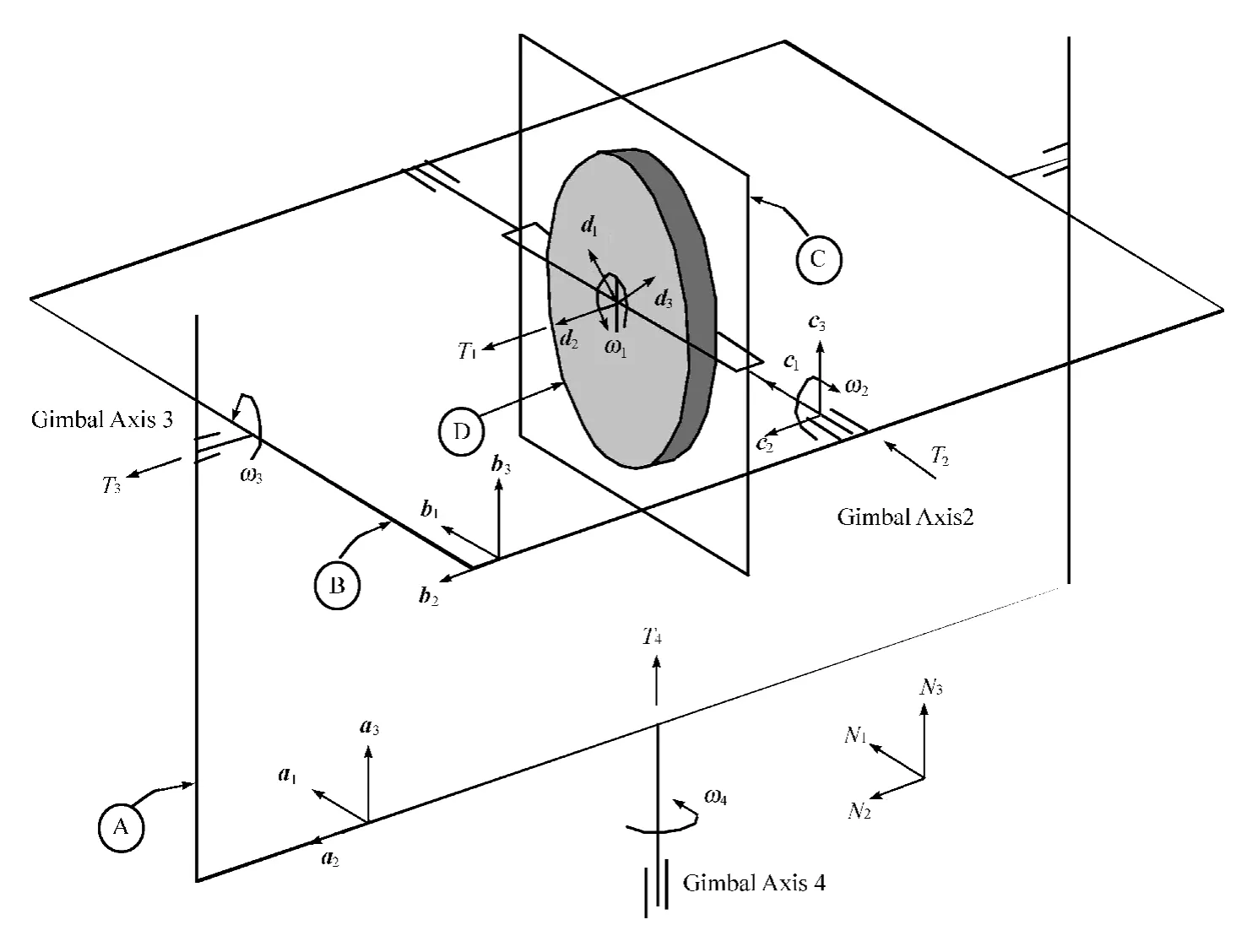
图5 坐标系

满足右手定则的正交单位向量ai、bi、ci和di(i＝1,2,3)分别固定在框架A、B、C、和D上,组成4个固连坐标系,分别对应的4个转动轴为轴4、轴3、轴2和轴1。惯性参考坐标系定义为N,由满足右手定则的单位正交向量Ni(i＝1,2,3)构成。转子D在d2方向的角位移定义为q1;在本装置的动力学分析中不会用到转子的移动,故通常考虑框架C中D的速度为ω1; q2定义为C绕c1相对B的转角;q3为B绕b2相对A的转角,q4被定义为A绕a3相对N的转角。4个角度确定了系统的构形,图5的构形对应的角度为qi＝0 (i＝1,…,4)。

系统的所有部件的质心位于转子D的中心,它也是所有框架轴的中心。因此,在以下分析中,只考虑旋转动力学,重力作用忽略不计。组成系统的所有部件的主惯性矩阵I如式(1)。注意每个矩阵都是在固连于各自部件的坐标系中给出的。Ix,Jx,Kx(x＝A,B, C,D)分别是在部件A、B、C和D中绕第i(i＝1,2,3)方向的标量转动惯量。

由于所有的质心都是位于N上的,所以组成该系统的所有部件的质心的线速度都为零。分析中只需要考虑角速度。A在N中的角速度ωA,N为

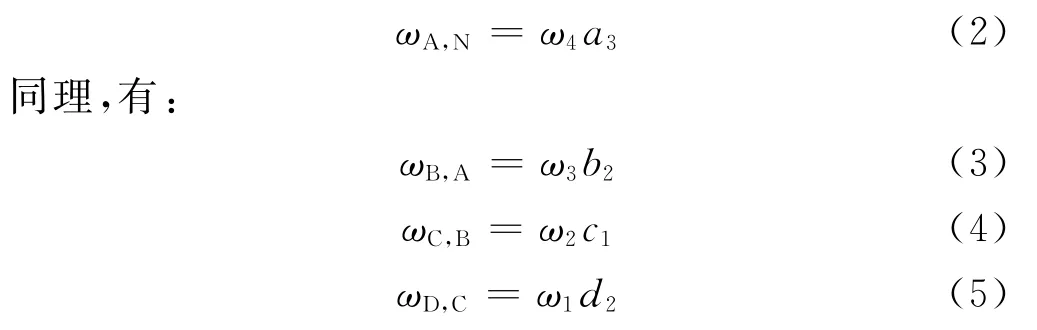
广义坐标与角速度相关联的运动学微分方程为:

最后,通过如下转换矩阵使每个部件的坐标系都可以转换到惯性坐标系,有如下关系式:

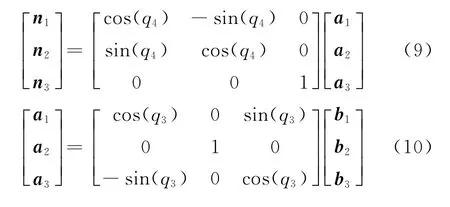
系统需要考虑2个输入。第一个输入是通过转子式旋转电机,由C施加于D的转矩T1,其结果是C和D上有以下转矩:

第二个输入是由B施加于C的转矩T2,其结果是C和B有如下转矩:

方程(1)—(16)唯一地确定了系统的动力学构形。通过拉格朗日方程可以求解运动方程,其形式为

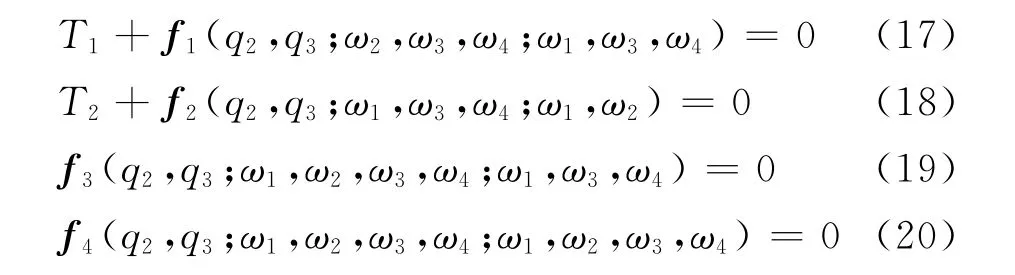
根据方程(17)—(20)在操作点附近的泰勒级数展开式的前两项,就可求出其线性化运动方程。稳定平衡点被定义为ω1＝Ω,q2＝q20,q3＝q30则线性化方程为

上面的等式表示的是装置在任意操作点下,各种可能构形的线性动力学,当指定装置为某一种构形时,数学模型将会相应的变化。

3 PID控制器的设计

在本实验中,装置的构形如图6所示,对应的运动模型如图7所示。框架C的表面与框架B的表面相互垂直,框架A的角度是任意的,轴3的制动器是关的,所以框架B的位置是自由的,框架C和A的位置是锁定的。

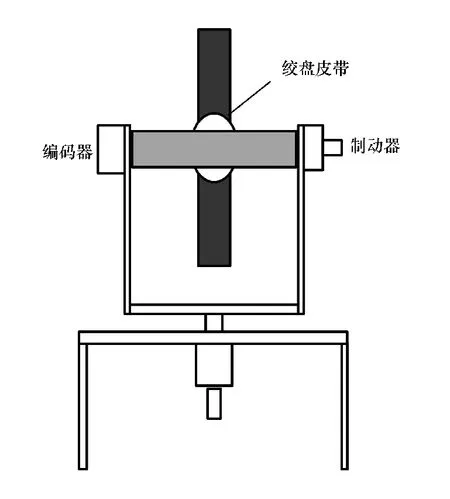
图6 装置构形

图7 运动模型

根据上述指定的装置构形可以进一步简化控制力矩陀螺的动力学方程。在这种配置下,操作点都是在框架角度q20＝0,q30＝0,ω1＝Ω附近。其中,Ω为转盘D的转速,则方程变为:

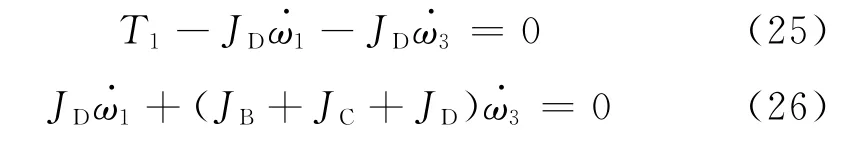
可以得到如下传递函数:

以上述传递函数为控制对象,加入PID控制器,得到图8所示的控制框图。

闭环传递函数为

其中,kp、kd、ki分别为比例系数、微分系数和积分系数,kA3表示控制效果增益,J3＝JB＋JC。

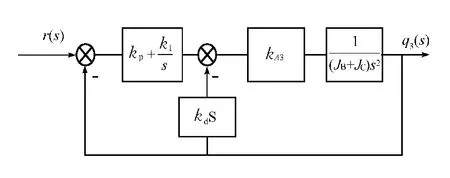
图8 系统控制框图

只考虑PD控制(ki＝0)时,传递函数可以简化为

传递函数可进一步表示为

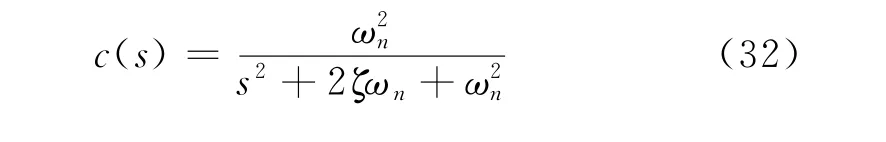
4 控制器参数计算及实验仿真

4.1 参数计算

系统的硬件增益kA3＝－1.04,J3＝0.04。设定系统自然频率ωn＝3 Hz,则根据式(30)可计算kp＝0.35。再设计kd参数来实现3种阻尼情况:(1)ζ＝0.25(欠阻尼);(2)ζ＝1.0(临界阻尼);(3)ζ＝1.6(过阻尼)。由公式(31)可计算3种情况的参数分别为kd＝0.057,0.23,0.37。

在临界阻尼时,加入积分控制,根据kikA3＝50 Nm/(rad·s－1)计算得到ki＝48。

4.2 仿真验证

设置采集编码器1、编码器3、命令位置1和控制效果1的数据。建立一个闭环阶跃,其幅值为零,停留时间为5 000 ms,重复次数为1,输入3种阻尼下的控制器参数,并加载到控制器中,设置数据采集,绘制仿真图形。PD控制器作用下的对象的阶跃响应曲线见图9,临界阻尼的PID控制器的阶跃响应曲线见图10。

通过比较加入积分环节前后的图形可知,增加积分的作用可以消除稳态误差。

5 结论

本文主要介绍了ECP公司的控制力矩陀螺装置的结构组成,推导了数学模型,并为其设计了控制器。这套设备和目前其他类型的陀螺装置相比,性能优异且具备完善的实验仿真功能,为学生学习控制力矩陀螺的原理和仿真实践提供了有力支持。

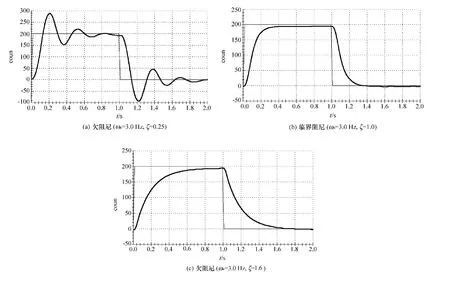
图9 3种阻尼的PD控制器阶跃响应曲线

图10 临界阻尼的PID控制器阶跃响应曲线

References)

[1]Lappas V J,Steyn W H,Underwood C.Design and Testing of A Control Moment Gyroscope Cluster for Small Satellites[J].Journal of Spacecraft and Rockets,2005,42(4):729-739.

[2]吴忠,张激扬.控制力矩陀螺框架伺服系统动力学建模与控制[J].应用基础与工程科学学报,2007,15(1):130-136.

[3]Sanjay P B,Panwan K T.Controllability of Spacecraft Attitude U-sing Control Moment Gyroscope[J].IEEE Transactions on Automatic Control,2009,54(3):585-590.

[4]Seraji H.Configuration Control of Redundant Manipulators:Theory and Implementation[J].IEEE Transactions on Robotics and Automation,1989,5(4):472-490.

[5]Bedrossian N S,Paradiso J,Bergmann E V,et al.Redundant Single Gimbal Control Moment Gyroscope Singularity Analysis[J].Journal of Guidance Control and Dynamics,1990,13(6): 1096-1101.

[6]吴忠,吴宏鑫.单框架控制力矩陀螺操纵律研究综述[J].宇航学报,2000,21(4):140-145.

[7]张锦江,李季苏,吴宏鑫,等.大型航天器SGCMG系统的奇异性分析研究[J].中国空间科学技术,2001(3):36-41.

[8]汤亮,贾英宏,徐世杰.使用单框架控制力矩陀螺的空间站姿态控制系统建模与仿真[J].宇航学报,2003,24(2):126-131.

[9]张锦江,李季苏,吴宏鑫.用单框架控制力矩陀螺的大型航天器姿态控制系统实物仿真研究[J].宇航学报,2004,25(4):382-388.

[10]吴忠.单框架控制力矩陀螺动态操纵律设计[J].宇航学报,2005, 26(1):24-28.

[11]吴忠,魏孔明.基于非线性观测器的控制力矩陀螺操纵律设计[J].北京航空航天大学学报,2006,32(11):1295-1298.

[12]汤亮,徐世杰.采用变速控制力矩陀螺的航天器自适应姿态跟踪和稳定控制研究[J].航空学报,2006,27(4):663-669.

Design of controller for control moment gyroscope based on PIDmethod

Wang Jiawei,Yang Yafei,Qian Yuheng
(Experiment and Training Center for Flight Vehicle Control,Harbin Institute of Technology,Harbin 150001,China)

The control moment gyroscopes(CMG)are widely used in spacecrafts such as satellites and space stations as actuators of attitude control.In order to grasp the principle of the control moment gyroscope,the structure of Model750 is introduced and the mathematical model of the device has been deduced.Then,the controller is constructed for Model750 by using PID method and the parameters of controller are designed.Lastly,the simulation graphs are given.

control moment gyroscope;design of controller;PID

TP271;V448.2

A

1002-4956(2015)4-0092-06

2014-09-25

黑龙江省教学研究项目(JG2013010268)

王佳伟(1982—),男,黑龙江哈尔滨,在读博士研究生,工程师,研究方向为控制系统实验与故障诊断技术.

E-mail:wangjiawei1982＠163.com