一种TlADC系统时钟偏斜误差的全并行校正方法
聂 伟,邱 蓉
(北京化工大学计算机系统与通信实验中心,北京 100029)
一种TlADC系统时钟偏斜误差的全并行校正方法
聂 伟,邱 蓉
(北京化工大学计算机系统与通信实验中心,北京 100029)
给出了一种TIADC系统时钟偏斜误差全并行结构的校正方法。该方法利用串并转换实现高速数据的降速,再利用滤波器的多相分解技术构建一个16×16的滤波器阵列对时钟偏斜误差进行实时校正,不但可以有效地减小杂散频谱,而且当输入信号从10 MHz变化至500 MHz时,系统校正后的SFDR平均提高了30.64 dB。仿真结果表明了该方法的正确性和有效性。
TIADC系统;时钟偏斜误差;完美重构;全并行校正
增益误差和偏置误差用加法和乘法就可以实现校正[6],而时钟偏斜误差的校正则比较复杂,主要有4种方法,即内插法[7]、自适应法[2,8]、基于分数延迟滤波器[5,9]方法以及完美重构法[4,6,10]。前两种方法计算比较复杂,很难实现实时修正;第三种方法需要过采样,限制了采样率的提高;完美重构法采用并行结构实现,具有计算时间短的优点,能较好地解决实时校正问题。完美重构法采用滤波器组进行校正,并用多通道滤波来降低对处理速度的要求,但仍然不适合高速场合。
本文在分析了时钟偏斜误差的产生及其对系统的影响后,基于完美重构算法,给出了一种全并行结构的校正方法,该方法利用串并转换将高速数据降速,再利用滤波器的多相分解技术构建了一个16× 16的滤波器阵列对时钟偏斜误差进行校正。这种全并行结构大大提高了系统的数据处理速度,可以应用于高速环境。
1 TIADC系统时钟偏斜误差的分析
TIADC系统的原理框图见图1。从图1中可以看出,M个通道的TIADC系统需要相同数量的ADC,采样时将带限信号送ADC,并在相同频率、不同相位的时钟下进行采样。
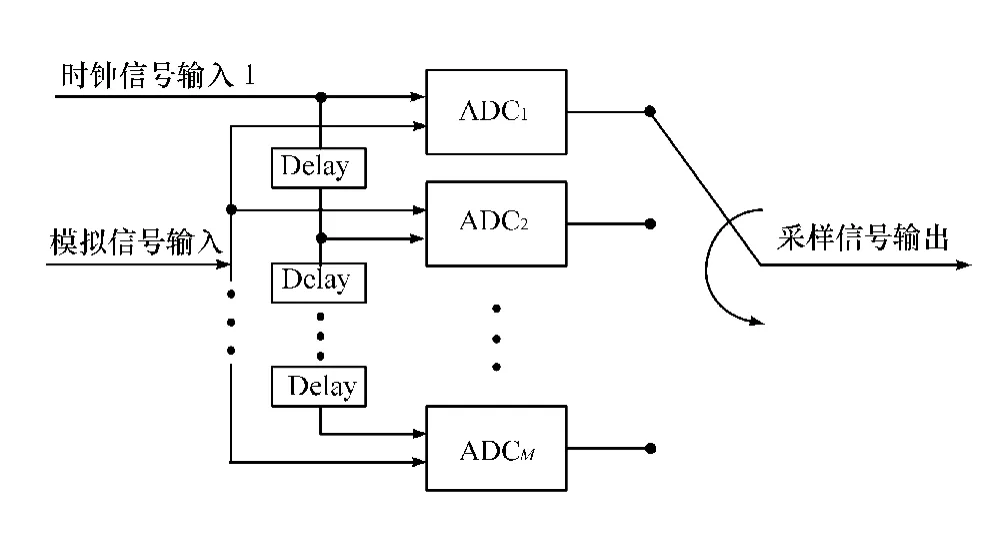
图1 TIADC系统的原理框图
理论上,每个ADC的采样时钟具有相同的频率和固定的相位差,但实际上时钟生成电路和传输路径不可能完全一致,因此理想时钟和实际时钟之间存在相位偏差,如图2所示。
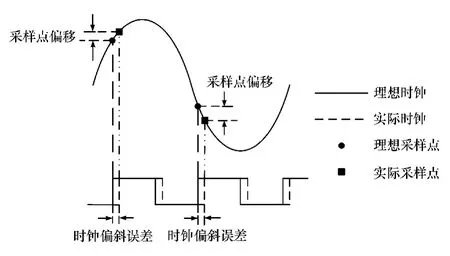
图2 TIADC系统的时域示意图
由于相位偏差使采样点发生偏移,均匀采样变成了非均匀采样,导致系统的输出信号频谱失真,严重影响系统的信噪比及其无杂散动态范围等。
假设输入信号为u(t)=A ejω0t/Ts,Ts为系统采样周期,每个子通道的采样时钟周期为MTs,那么第m通道的时间偏斜误差可以表示为为rmTs,rm为m通道时间偏斜误差系数,m=0,1,...,M-1,其采样时间tm为
(3)对剪力墙抗震设计计算,要正确选择非线性分析中的计算模型和各种计算参数;对采用滑动支座的结构进行大震下的抗震设计计算,采用的计算模型应考虑支座两侧结构的相互作用和影响;对平面尺寸凹凸不规则,以及平面内局部开设大洞口的结构进行抗震设计计算时,应根据开设洞口大小、数量和分布位置以及抗侧力构件的布置形式等合理建立计算模型。
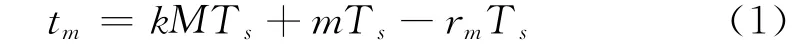
于是采样后的序列可以写成
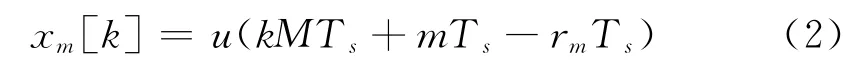
最终的输出序列可以表示为
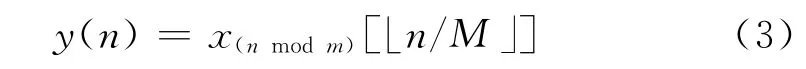
对式(3)进行FFT变换,可以得到频谱:
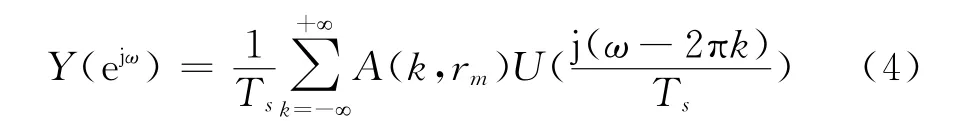

2 误差的校正
2.1 完美重构校正法
完美重构校正法的原理框图如图3所示。
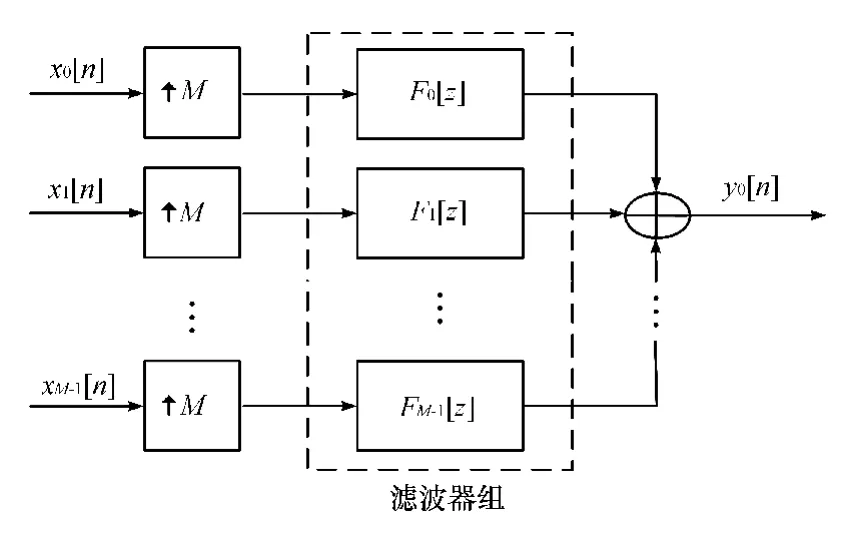
图3 基于完美重构校正法的原理框图
从图3中可以看出,该方法是先将ADC采样后的数据xm(n)进行M倍内插,然后通过滤波器组Fm(z)进行滤波校正,最后将滤波器的输出相加,即可得到校正后的数据。该滤波器组可以表示为:
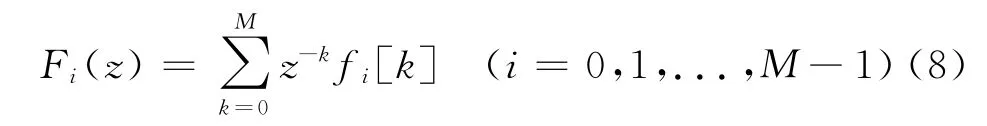
其中,fi[k]是滤波器的系数,可以根据下面公式计算:
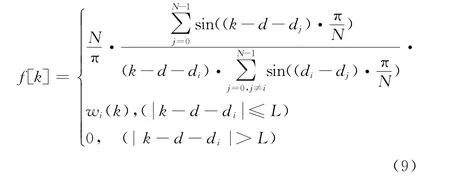
为了在高速环境中进行时钟偏斜误差的实时校正,本文在完美重构算法的基础上给出了一个全并行结构,可以有效地提高处理速度。下面以4通道ADC为模型来进行说明。
2.2 全并行结构校正法
全并行实时校正方法的整体结构如图4所示。带限模拟信号xin(t)同时输入4个ADC,令fs=1/Ts,每个ADC通道的采样时钟(由外部时钟提供)周期均为4Ts,其相位依次相差90°,那么整个系统的等效采样率为fs。
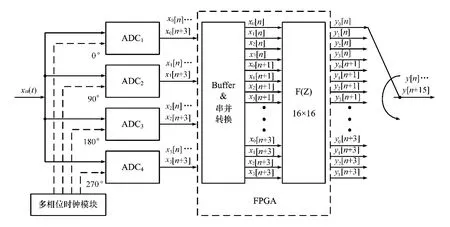
图4 全并行结构校正法的原理框图
采样之后,ADC的输出数据流x0[n]、x1[n]、x2[n]、x3[n]由FPGA缓存,利用FPGA的内部逻辑将缓存后的4路并行数据进行串并转换,转换成16路并行数据流:
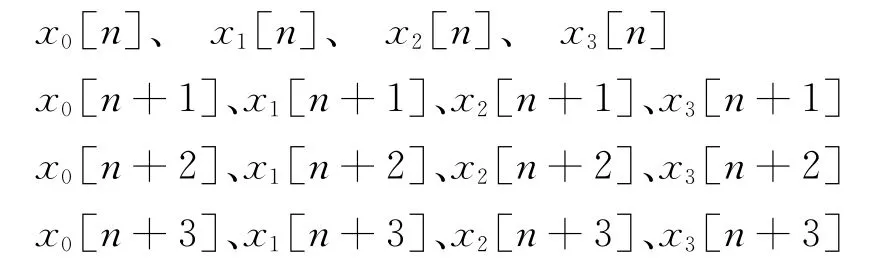
即对4路数据流分别做4倍的抽取,然后按照采样先后顺序对齐,并送16×16的滤波器阵列进行滤波校正。由于同一个通道抽取后的数据流与原始的数据流有着相同的时钟偏斜误差,因此这16路数据流的相位信息可以表示为
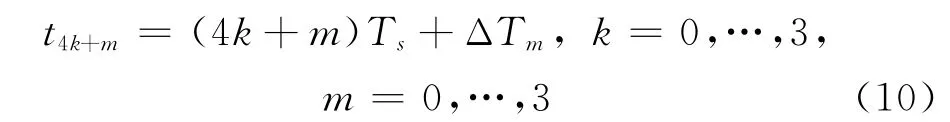
其中,m是指原始的通道,而4k+m是指抽取后的通道。
16×16的滤波器阵列可以表示成
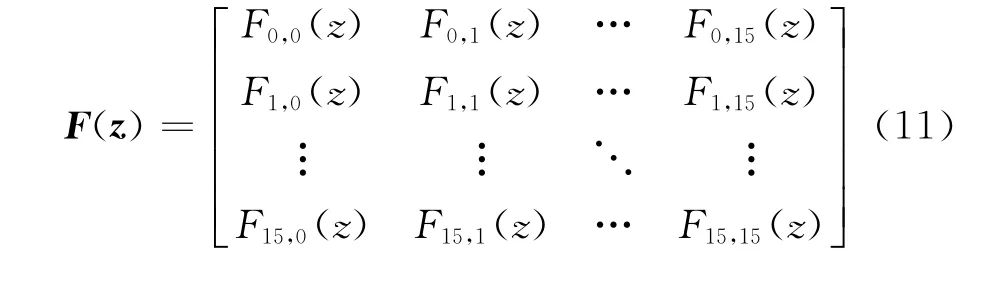
其中,每个元素Fj,i(z)都可以由滤波器组里的Fi(z)计算得到,即
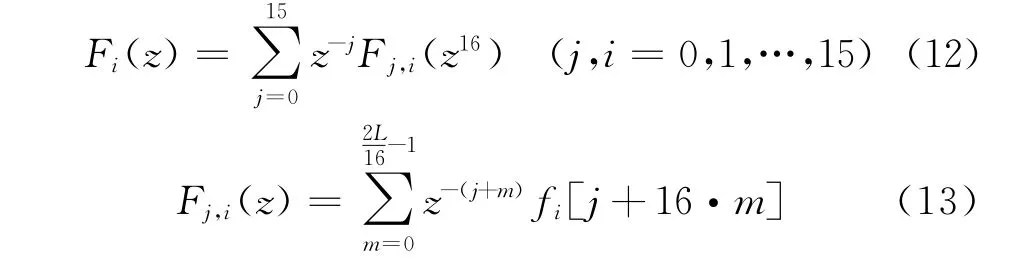
式(13)中,fi[j+16·m]为滤波器系数,可以由公式(9)计算。
滤波校正过程可以由下式表示:
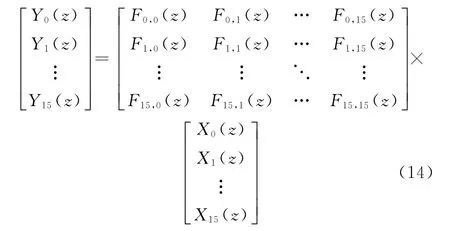
其中,Xi(z)表示16路输入数据,Yi(z)表示滤波后的16路输出数据,通过多路选择重组为校正后的数据。其数据流的流向如图5所示。
从图(5)中可以看出,每个输出数据流由16个不同通道的滤波器的输出相加得到,然后按顺序组合成最终的输出,即校正后的采样数据。
3 仿真及性能分析
为了估算全并行结构校正法的性能,本文在Matlab平台上对一个8位4通道的TIADC系统做了仿真。假设该系统每个子通道的采样率均为400 MHz,那么总的采样率就是1 600 MHz,其增益误差和偏置误差均为零,而4个通道的时间偏斜误差分别为[0, -0.01,0.02,0.01]Ts。
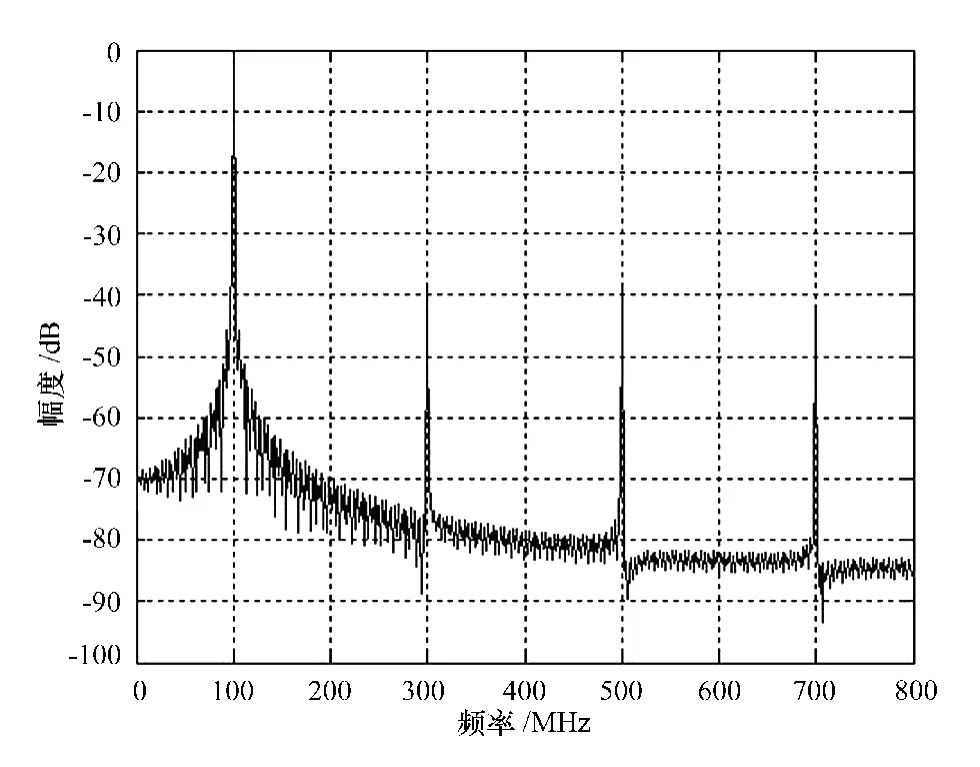
图6 校正前的频谱
为了验证全并行校正法的正确性和有效性,分别对采样后的4路原始数据做1∶4的串并转化,形成16路数据,此时这16路数据的时间相位信息可以根据公式(11)计算,结果为[0,0.99,2.02,3.01,4,4.99, 6.02,7.01,8,8.99,10.02,11.01,12,12.99,14.02, 15.01]。根据此时间相位信息可以计算出16个ADC通道每个通道对应的校正滤波器的系数,阶数为64(即2L=64),即公式(12)中的Fi(z)可以分解为16 个4阶的子滤波器Fj,i(z),从而得到16×16的滤波器阵列,即F(z),然后进行误差校正。
图7显示了校正后的频谱图,图中时间偏斜误差引起的失真谱线的幅度大大减小。从校正前和校正后的频谱可以看出,当输入信号为100 MHz时,校正后系统的SFDR性能有了很大的改善。
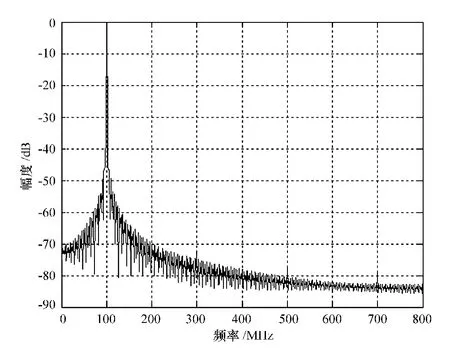
图7 校正后的频谱
为了获得不同频率的输入信号的校正结果,本文选取了10~500 MHz范围内的一系列频点进行仿真,并计算了各频点校正前和校正后的SFDR,结果比较如图8所示。从图8可以看出,对于不同频率的输入信号,本文的校正算法都可以有效地完成校正,但校正效果随着输入信号频率增加而有所减弱,系统SFDR平均提高了30.64 d B,其性能得到了较大的改善。
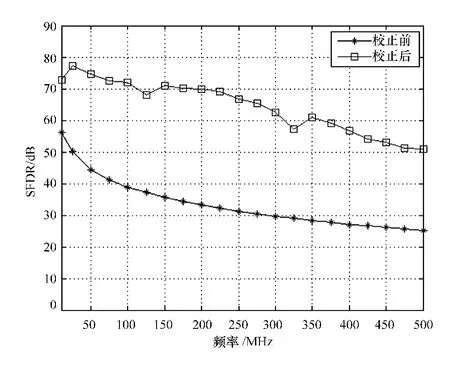
图8 校正前后系统的SFDR比较
4 结束语
本文给出了一种适用于高速环境实时校正的全并行校正方法,并在Matlab平台上构建了一个4通道的TIADC系统,利用全并行校正法对其进行滤波校正,并且在10~500 MHz范围内选取了一系列频点进行仿真。仿真结果表明,该方法不但可以有效地减小杂散频谱,而且当输入信号频率变化时,系统校正后的SFDR平均提高了30.64 dB。该方法可以应用于示波器、波形数字化仪等仪器,具有很好的应用前景。
References)
[1]Black Jr W C,Hodges D.Time interleaved converter arrays[J].Solid-State Circuits:IEEE Journal of Solid-State Circuits,1980,15 (6):1022-1029.
[2]秦国杰,刘国满,高梅国,等.一种时间交替ADC时间失配误差自适应校正方法[J].仪器仪表学报,2013(12):2730-2735.
[3]Kurosawa N,Kobayashi H,Maruyama K,et al.Explicit analysis ofchannel mismatch effects in time-interleaved ADC systems[J].Circuits and Systems I:Fundamental Theory and Applications,IEEE Transactions on,2001,48(3):261-271.
[4]Lim Y C,Zou Y X,Lee J W,et al.Time-interleaved analog-to-digital-converter compensation using multichannel filters[J].Circuits and Systems I:Regular Papers,IEEE Transactions on,2009,56 (10):2234-2247.
[5]刘艳茹,田书林,王志刚,等.一种基于Farrow滤波器的并行采样时间误差校正[J].电子测量与仪器学报,2010(1):50-54.
[6]周浩,赵雷,李玉生,等.基于数字后处理算法的并行交替采样ADC系统[J].数据采集与处理,2010(4):537-543.
[7]Selva J.Functionally weighted Lagrange interpolation of band-limited signals from nonuniform samples[J].Signal Processing:IEEE Transactions on,2009,57(1):168-181.
[8]Liu S J,Qi P P,Wang J S,et al.Adaptive Calibration of Channel Mismatches in Time-Interleaved ADCs Based on Equivalent Signal Recombination[J].Instrumentation and Measurement,IEEE Transations on,2014,63(2):277-286.
[9]Johansson H,Lowenborg P.Reconstruction of nonuniformly sampled bandlimited signals by means of digital fractional delay filters [J].Signal Processing:IEEE Transactions on,2002,50(11): 2757-2767.
[10]Jenq Y C.Perfect reconstruction of digital spectrum from nonuniformly sampled signals[J].Instrumentation and Measurement: IEEE Transactions on,1997,46(3):649-652.
A full parallel correction method of time skew error for TIADCsystem
Nie Wei,Qiu Rong
(Computer System and Communication Laboratory,Beijing University of Chemical Technology,Beijing 100029,China)
This paper presents a full parallel correction method of time skew error for TIADC system.And the method can not only utilize serial-to-parallel conversion to realize reduction of speed for high speed data,but also make use of polyphase decomposition technique to build a 16×16 filter array to correct the time skew error in real time.The time skew error can be largely and well calibrated by this method,moreover,When the input signal changes from 10 MHz to 500 MHz,the SFDR of the system after correction raises 30.64dB averagely.The simulation results indicate the correctness and effectiveness of the method.
TIADC system;time skew error;perfect reconstruction;full parallel correction
TN713
A
1002-4956(2015)4-0047-05
2014-11-12
聂伟(1960—),男,山西太原,博士,副教授,研究方向为软件无线电、通信信号处理等.
E-mail:niewei@mail.buct.edu.cn

