桩底土为标准线性体模型时层状土体中桩顶振动响应

韩红霞，崔武文，李栋

（1.河北工业大学土木工程学院，天津 300401；2.天津财经大学商学院，天津 300222）

桩底土为标准线性体模型时层状土体中桩顶振动响应

韩红霞1，崔武文2，李栋1

（1.河北工业大学土木工程学院，天津 300401；2.天津财经大学商学院，天津 300222）

研究了桩侧土为广义Vogit体模型，桩底土为标准线性体模型，层状场地土体中桩的纵向振动特性．首先利用拉普拉斯变换并引入初始条件和边界条件，推导出位移阻抗函数．之后根据阻抗函数的传递性求得了在简谐激振力作用下桩顶频域响应解析解．最后结合具体算例，分析了考虑桩底土为标准线性体条件下，桩侧土体剪切波速的变化对桩顶速度导纳曲线的影响．研究表明：土体剪切波速的变化对对桩顶速度导纳曲线峰值影响较大，对曲线的振动频率影响很小．层状场地土体特性相差越大，桩顶速度导纳曲线峰值越大．正常沉积土层中桩顶速度导纳曲线峰值明显大于非正常沉积土层．

广义Vogit体；标准线性体；成层土；纵向振动

桩基检测是判断桩基施工质量的重要依据．桩的纵向振动理论可以为桩基检测提供理论依据，因此，对桩竖向振动的理论研究有着非常重要的理论和工程实践价值．实际工程中，桩周土体多为层状，对层状场地中桩的纵向振动特性的研究显得尤为重要．目前，国内外对此问题已进行了广泛的研究．Novak[1]利用传递矩阵法求得了在简谐激励力作用下成层土中桩顶的阻抗函数．Nogami[2]通过用多项式的形式来模拟桩身位移，通过传递矩阵求得了成层土中桩顶的时域响应，并将土体的平面应变模型在连续体的基础上进行了拓展．胡昌斌[3]对成层土中桩土纵向耦合振动时的桩顶时域响应进行了解析研究．杨冬英[4-5]等采用连续介质模型对非均质土中桩的纵向振动特性进行了研究．

标准线性体模型[6-7]不仅能够反映土体随频率变化的趋势，还能够精确地反映土体的松弛及蠕变特性，然而对考虑桩周土体为标准线性体时桩顶纵向振动特性的研究还很少．在此基础上，本文主要研究了桩底土为标准线性体，桩侧土为双Vogit模型时，层状场地土体中桩顶纵向振动特性．采用拉普拉斯变换及阻抗传递函数求得桩顶速度频域响应函数的解析表达，然后利用卷积定理和傅氏逆变换求得在半正弦脉冲激振力作用下桩顶的速度时域响应的积分形式解，研究了层状场地土体中桩底土为标准线性体时桩的纵向振动特性．

1 计算模型

计算模型基本假定如下：

1）桩为有限长等截面均匀竖直杆，其材料为质量连续分布的线弹性体．弹性模量为E、桩长为L．Ai、i、Ci分别为第i（1in）层土体内桩的面积、材料密度和弹性纵波波速．

2）桩侧土体根据土层参数不同分为n层，从下到上依次为第1、2、、n层；对应厚度为h1、h2、、hn．假设各层土体为均质、连续的线弹性体，采用广义Voigt模型近似模拟（如图1所示），分布式弹簧系数和阻尼系数如图1所示．

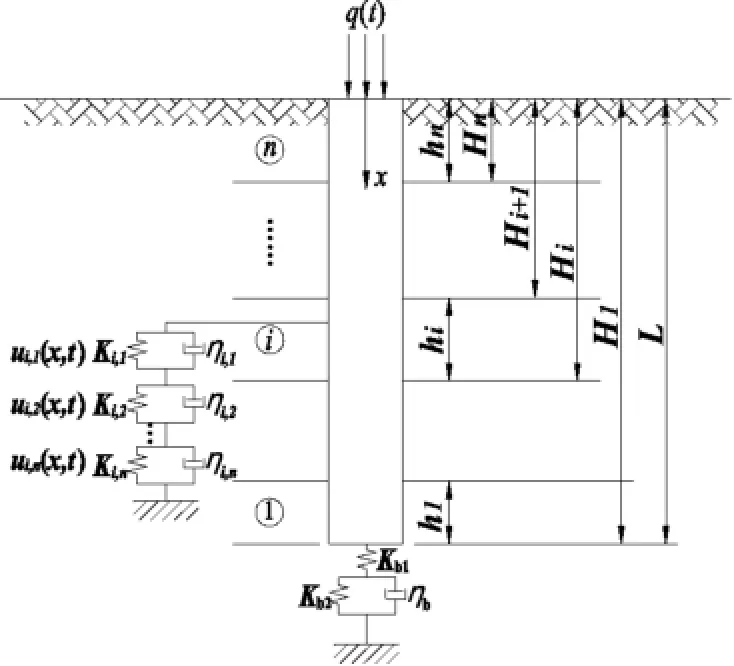
图1 计算模型简图Fig.1Diagram of calculation model

3）桩底土采用标准线性体模型近似模拟．分布式弹簧系数为kb1、kb2、阻尼系数为b．

4）激振力为作用于桩顶沿竖直方向的均布振动荷载．假设桩纵向振动时，桩土体系仅发生线性变形，忽略桩周围土体的水平径向位移．

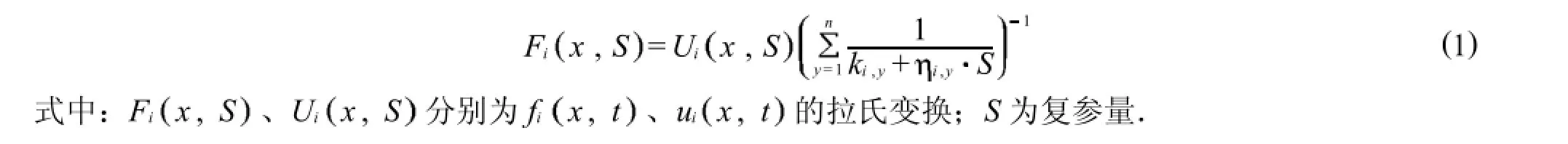
2 定解问题的建立

3 定解问题的求解

图23 个Vogit体串联模型Fig.23 Voigt model series model

4 土的成层性对于桩土系统振动特性影响分析

桩侧土为的广义Vogit体，应考虑土的动力学特性，并依据现实勘探中土层的情况和桩的施工情况选取．国外学者Nogami、Konagai、Novak[2，8]等人的研究成果表明，在桩周土满足连续介质平面应变假定条件下，圆形截面桩作纵向振动时桩周土的动力作用可以用3个Voigt体串联模型近似地代替（如图2），

有关参数的建议取值如下

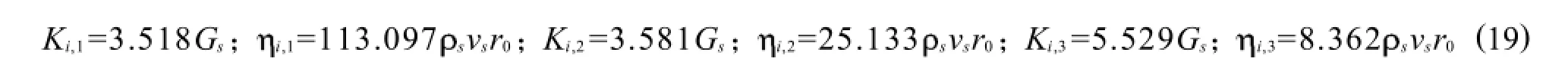
式中：Gs、s、vs分别为桩周土的剪切模量、密度、剪切波速；r0为该桩段的截面半径．

把式(19)中的模型有关参数转换成无量纲化参数，其具体转换关系[9-10]如下

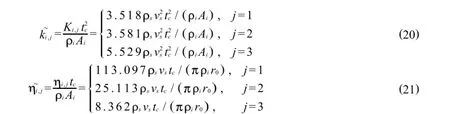
由式(20)、式(21)可得到任意层土中桩的速度响应曲线，下面通过一个具体完整桩的算例来进行研究．

有一半径为500 mm圆形截面预制桩，长度为10 m，采用C30混凝土，一维弹性纵波速为3 500 m/s，桩材料密度为2 600 kg/m3．桩侧土分为以下3种情况：

1）上层为8 m淤泥质粘土，土密度为1 700 kg/m3，土层剪切波速110 m/s；下部8 m为稍密粉土，其湿密度为1 940 kg/m3，土层剪切波速150 m/s；

2）上层为8m淤泥质粘土，参数同“1）”；下部为8m密实中细砂，其湿密度为2110kg/m3，土层剪切波速230 m/s；

3）上层为8 m淤泥质粘土，参数同“1）”；下部为8 m中密卵砾石层，其湿密度为2 270 kg/m3，土层剪切波速310 m/s．

结合这3种土体实际分层情况，根据式(20)、式(21)进行换算可得到各自情况下的桩周土模型参数如表1．

根据上述参数，计算得到桩周土为正常沉积土层（即上软下硬土层）桩顶速度频幅曲线如图3所示．可以看出，对于这种正常沉积的土层，随着第2层土体剪切波速的增大，桩顶速度导纳曲线峰值逐渐减增大，而曲线振动频率不变．对某一土层情况而言，曲线共振峰值随着频率的增加而增大，最终趋于稳定．

为了进一步了解土层软弱变化对于桩顶频域相应的影响，将算例中上下土层对换，计算得到桩周土为非正常沉积土层时桩顶速度频幅曲线如图4所示．可以看出：对于非正常沉积土层即上部土层剪切波速大于下部土层，两层土体剪切波速相差越大，共振峰值越高，反之，则曲线比较平缓．从波峰的高度来看，正常沉积土层明显大于非正常沉积土层．

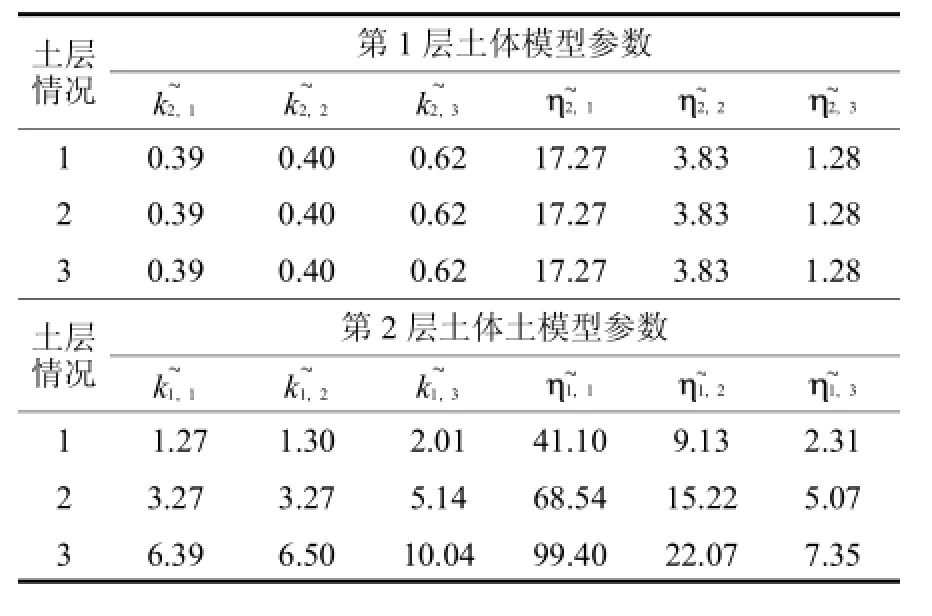
表13 种情况下的土模型参数值Tab.1Parameters of soil model

5 结论

1）本文建立了桩侧土为广义Vogit体，桩底土为标准线性体的成层土中桩的纵向振动模型，首先确立相应的边界条件和基本方程，然后利用了阻抗函数具有的递推特性推导出桩顶频域响应函数，最后将广义Vogit体简化为3个Vogit体模型，利用具体的算例分析了桩顶的速度频域响应，使得研究更具有实际意义．

2）对于正常沉积土层，下层土体剪切波速的变化对曲线的振动频率没有影响，而对曲线峰值影响较大，两层土体特性相差越大，曲线振动峰值越大．

3）对于非正常沉积土层，上层土体的剪切波速变化对曲线的振动频率没有影响，对曲线峰值影响较大，两层土体特性相差越大，曲线振动峰值越大，这一点与正常沉积土层一致．不同的是正常沉积土层的振动峰值明显大于非正常沉积土层．

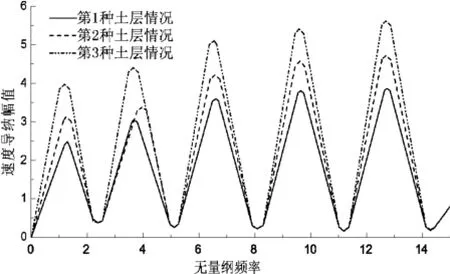
图3 正常沉积土层桩顶速度频幅曲线Fig.3The velocity admittance curve of normal sedimentary soil

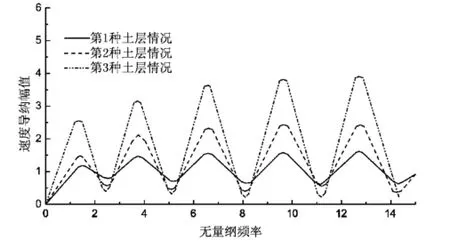
图4 非正常沉积土层桩顶速度频幅曲线Fig.4The velocity admittance curve of abnormal sedimentary soil

[1]NovakM，Aboul-EllaF．ImpedanceFunctionsofPilesinLayeredMedia[J]．JournaloftheEngineeringMechanicsDivision，1979，104（3）：643-661．

[2]Nogami T，Konagai K．Time domain flexural response of dynamically loaded single piles[J]．Journal of the Engineering Mechanics，1988，114（9）：1512-1525．

[3]胡昌斌，黄晓明．成层粘弹性土中桩土耦合纵向振动时域响应研究[J]．地震工程与工程振动，2006，26（4）：205-211．

[4]杨冬英，王奎华，丁海平．双向非均质土中基于连续介质模型的桩动力响应特性分析[J]．土木工程学报，2013，46（3）：119-126．

[5]杨冬英，王奎华，丁海平．三维非均质土中粘弹性桩-土纵向耦合振动响应[J]．土木建筑与环境工程，2011，33（3）：80-87．

[6]何平笙，朱平平，杨海洋．高聚物粘弹性力学模型的等当性[J]．高分子材料科学与工程，2010，26（11）：169-171．

[7]李成波，Adnan Aydin，施行觉，等．岩石蠕变模型的比较和修正[J]．实验力学，2008，23（1）：10-16．

[8]NovakM，NogamiT．Dynamicsoilreactionforplanestraincase[J]．Journal ofGeotechnicalandGeoenvironmentalEngineering，1978，104：953-95．

[9]王奎华．成层广义Vogit地基中粘弹性桩纵向振动特性分析与应用[J]．浙江大学学报（工学版），2002，36（5）：59-63．

[10]王奎华，应宏伟．广义Voigt土模型条件下桩的纵向振动响应与应用[J]．固体力学学报，2003，24（3）：293-303．

Pile vibration response in layered soil for standard linear model of subsoil

HAN Hongxia1，CUI Wuwen2，LI Dong1

(1.School of Civil Engineering,Hebei University of Technology,Tianjin 300401,China;2.School of Business,Tianjin University of Financial and Economics,Tianjin 300222,China)

This paper studies vertical vibration characteristics of pile in layered soil when the pile subsoil is assumed as standard linearmodeland thelateralsoilis assumedasVogitmodel.The displacementimpedancefunctionisderived based on Laplace transform and boundary condition between pile and soil.According to the transfer function of the impedance the frequency response solution of pile top is calculated at the harmonic excitation force.Finally,a numerical example is analyzed considering pile subsoil as standard linear model.The results showed that the soil shear wave velocity has great effect on the peak of velocity admittance curve and little effect on the vibration frequency.The difference of layered soil characteristics is bigger;the peak of pile top velocity admittance curve is greater.The velocity admittance curve of pile top in normal sedimentary soil is significantly higher than that in abnormal sedimentary layer.

generalized Vogit model;standard linear model;layered soil;vertical vibration

P315.9

A

1007-2373(2015)03-0089-05

10.14081/j.cnki.hgdxb.2015.03.017

2015-04-09

河北省住房和城乡建设厅应用研究项目（2010-254）

韩红霞（1975-），女（汉族），讲师，博士．