基于MYCIN不确定因子的区间灰数应急决策方法
蒋风光, 李 鹏, 陈立文
(1.河北工业大学 经济管理学院,天津 300401; 2.江苏科技大学 经济管理学院,江苏 镇江 212003; 3.天津职业大学 经济管理学院,天津 300410)
基于MYCIN不确定因子的区间灰数应急决策方法
蒋风光1,3, 李 鹏2, 陈立文1
(1.河北工业大学 经济管理学院,天津 300401; 2.江苏科技大学 经济管理学院,江苏 镇江 212003; 3.天津职业大学 经济管理学院,天津 300410)
主要研究了方案的指标值为区间灰数的快速应急决策方法。将MYCIN不确定因子融合到灰色决策理论中,通过计算各方案在不同指标下的MYCIN不确定因子并对其进行融合,确定最佳决策方案。建立了基于证据推理的应急决策方法,给出了区间灰数决策方法步骤;通过案例分析结果验证了所提方法的有效性。
区间灰数;MYCIN不确定因子;数据融合;应急决策
0 引言
近年来,世界各国频频发生重大突发性事件,这些事件有的属于自然灾害、有的属于人为破坏、有的属于事故灾难;如2001年美国的“9.11事件”,2003年我国的“SARS”事件,2003年8月的美国、加拿大等国大面积停电事故,2005年初的印度洋海啸,2005年的法国巴黎群体性骚乱,2006年的英国伦敦爆炸,2007年的印度安得拉邦连环爆炸,以及2008年5月我国四川省发生的特大地震等。非常规突发事件的发生给世界各国带来巨大的经济损失和人员伤亡,同时也向世界各国敲响了安全警钟。突发事件尤其是非常规突发事件,通常具有突然性、破坏性、蔓延性、不确定性、信息高度缺失性等特征,这给快速有效的应急处置和应急决策带来了很大的困难。如果无法做到及时、准确地进行应急处置或者做出错误的决策,就很有可能使其发展成为更大的灾难性事件,带来更大规模的伤亡和损失。
应对重大突发性事件进行应急决策时决策者所处理的信息往往是不完备、灰色或者模糊的,有些信息甚至是相互矛盾的,这给决策者进行决策带来了很大的困难。造成应急决策困难的主要原因是估计不准确或测量误差、或专家知识不完全,致使获取的数据具有不确定性。在处理不确定性决策问题上,Zadeh[1]提出模糊数学的方法,Chen[2]研究了模糊多属性决策方法,徐泽水和樊治平研究了不确定信息下模糊决策的排序问题[3,4],Moore等人对区间数进行了深入的探讨和研究[5~7],徐泽水和Sengupta研究了区间数的排序问题[8~10]。
灰色系统理论是描述不确定性问题的又一种方法,该方法用灰数来描述不确定信息。邓聚龙[11]首次提出灰色系统概念并用灰数表示不确定性问题。刘思峰[12,13]将灰色系统理论与模糊数学和概率统计方法进行了比较,分析其蕴含的信息。罗党[14]研究了观测值为区间灰数下的灰色关联度的算法,党耀国等[15]通过定义维区间数的距离公式,研究了基于区间数的灰靶模型。
传统的决策方法大都是对各方案的属性值加权求和得到各方案综合属性值,再根据其大小进行排序。事实上,在应对突发事件进行应急决策时,人们做决策除了用方案的属性值加权求和进行决策外,很多情况下,是利用个体的经验和所能收集到的相关事实与数据作为判断与推理的证据进行证据推理,进而找出最优方案的。在这里,我们称其为“证据推理决策”。目前,已有学者将证据理论融合到决策方法中,进行证据推理决策方法与模型的探讨[16~18]。Shafer等[16]针对单个证据不能全面反映事物运行规律的特点,研究了如何促进不同证据之间的有机融合,运用证据融合的结果表征复杂现象的本质。王育红等[17]将区间数与理论相结合得到区间数的决策方法。刘付显等[18]提出了基于不确定融合证据的决策方法。这些理论的提出和应用促进了证据理论、灰色系统理论和决策理论的进一步发展。
然而运用证据推理融合方法进行应急决策时,却存在二个方面的缺陷:
首先,在推理链较长时,合成公式的使用很不方便。因为随着推理过程增加,识别框架变得非常复杂,计算量大大增加;
其次,证据合成中会出现不稳定性,例如具有高冲突的证据合成会出现悖论,严重影响推理方法的应用。
针对传统决策方法以及证据理论与决策融合方法存在的上述问题,本文结合突发事件处置应急决策的特点,将MYCIN不确定因子方法引入到灰色决策理论中,提出一种基于MYCIN不确定因子的快速应急决策方法,主要创新之处有以下三点:
1)提供一种新的基于证据推理的快速有效的应急决策方法与模式,便于决策者方便地利用其已有的经验和应急处置动态决策过程中不断补充的新信息作为证据进行推理决策,从而保证大幅提高突发事件应急决策的准确率;
2)建立了证据推理合成公式,克服了证据推理决策模型计算工作量随推理链的增加而迅速大量增加和证据合成中出现的不稳定性问题的缺陷,大幅提高突发事件应急决策的效率;
3)将MYCIN不确定因子融入灰色决策问题中,建立了基于灰色推理的应急决策模型并设计了决策方法步骤,为人们利用灰色证据信息进行证据推理应急决策提供了方法依据。
1 决策模型构建与算法设计






理想属性偏离度作为两区间灰数之间的度量,可以将不确定性问题转化为确定性问题处理。
定义4[19]令长度为t(t≠0)的有限差异信息序列x=(x1,x2,…,xt)T,且至少存在xj≠0,j∈J,j={1,2,…,t}为序列的指标集,称映射
f:x→y
为有限序列x的信息结构算子,这里yj=(y1,y2,…,yt)T被称为信息结构映像序列。
由于决策矩阵A(⊗)=(aij(⊗))m×n的元素均以区间灰数形式给出,通过定义3所给出的理想属性偏离度公式将A转化为理想属性偏离度矩阵D=(dij)m×n,然后根据定义4得到信息结构映像序列矩阵Y=(yij)m×n。
定义5[20]设h是假设随机变量,e为证据随机变量,则CF(h/e)=MB(h/e)-MD(h/e)
为MYCIN不确定因子,其中
CF(h/e)表示当证据e肯定为真时,它对假设h为真的确定性程度,取值范围为[-1,1]。
当证据e不肯定为真时,用CF(e)表示证据e的可信度,取值范围是[0,1]。CF(e)的值越大表示证据e的可信程度越高;特别的,CF(e)=1表示证据e完全可信,CF(e)=0表示证据e完全不可信。
定义6 令CFT(h/e)=CF(h/e)·CF(e)为实质不确定因子。
实质不确定因子表征在出现证据e,证据e的可信程度为CF(e)的条件下,对假设h为真的确定性程度。

在利用MYCIN不确定因子方法进行决策的过程中,要想在较多的备选方案选择出比较理想的方案,需要对不同的证据信息进行融合,而在每个证据下,实质不确定因子的确定是进行信息融合的基础。结合信息结构映像序列和定义4,得到:
CFT(hi/ej)=CF(hi/ej)·CF(ej)=yij·(1-DOI(Ij))
(1)
其中,CFT(hi/ej)表示在指标Ij下方案Xi为最优方案的确定性程度,i=1,2,…,m,j=1,2,…,n。
定义8 设函数F:[0,∞)→[-1,1],满足
(1)F(0)=-1,F(∞)=1,F(X)是单调增的;
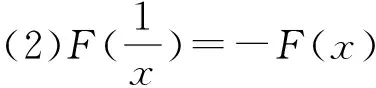
则称F为生成函数。
定义9 对于生成函数F(x),若存在二元函数f满足F(x·y)=f(F(x),F(y)),则称F为可合成的生成函数。



定理2 由F1得到的证据合成公式具有以下性质:
(1)CFT(h/e1,e2)=CFT(h/e1,e2),即交换律;
(2)CFT(h/(e1,e2),e3)=CFT(h/e1,(e2,e3)),即结合律。
证明 (1)交换律:
(2)结合律:
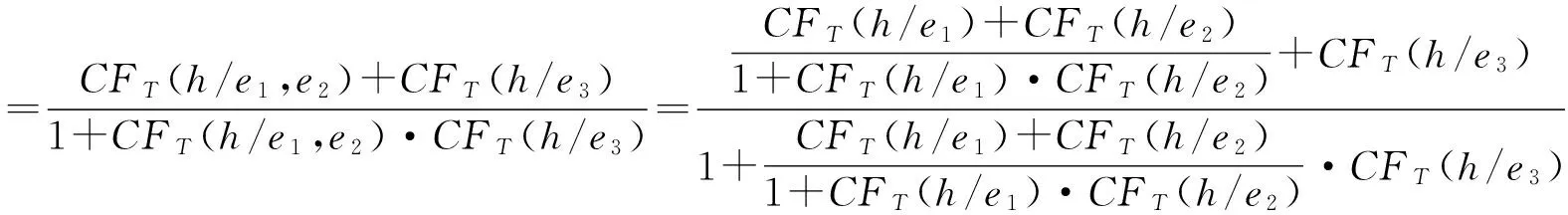

所以CFT(h/(e1,e2),e3)=CFT(h/e1,(e2,e3))。定理得证。


(2)
此推论提供了多条证据下实质不确定因子的融合方法。可以看到,MYCIN不确定因子在多个证据下进行融合是相当简便的,对于m个证据进行融合最多只需要m次运算。
综上所述,可以得到如下基于MYCIN不确定因子的区间灰数应急决策方法步骤:
步骤1 根据区间灰数矩阵选出理想属性区间灰数并计算理想属性偏离度矩阵D(dij)m×n;
步骤2 由理想属性偏离度矩阵和定义4得到信息结构映像序列矩阵Y=(yij)m×n;
步骤3 根据信息结构映像序列矩阵Y(yij)m×n和定义8得到指标Ij的不确信度DOI(Ij),j=1,2,…,n;
步骤4 根据信息结构映像序列矩阵和指标Ij的不确信度得到实质不确定因子矩阵CFT=(CFT(hi/ej))m×n;
步骤5 根据式(2)进行证据信息融合;
步骤6 根据实质不确定因子最大化原则选择最优方案。
2 实例分析
本节以伤员救助应急决策为例对所给方法进行案例分析。一般说来, 应急救灾的根本目标是减少突发事件中的人员伤亡和物质财产等损失,而在涉及人的突发事件中,减少人员伤亡又是绝对首要的目标。不同类型事件的特点可能会存在不同, 但是影响受灾人员挽救可能性的因素基本一致,大致可以分为以下5个方面:
(1)受灾人员的身体素质。 年龄、性别、身体健康状况等因素决定了受灾人员的身体综合素质,而身体素质的好坏同样是影响受灾人员生存能力的重要因素。
(2)受灾人员伤残状况。即突发事件发生时受灾人员的健康情况,主要包括受伤人员的伤亡病等情况。
(3)受灾人员的被困环境。它是指受灾人员在灾难发生后,评估及救援开始前所处的生存环境。
(4)受困时间。显然,受困时间越短,生存可能性就越高,救援的意义就越大。
(5)受灾人数。一般情况下,受灾总人数越多,进行应急救援所需的人力、物力等资源就越多,救援的难度就越高。
设某地发生地震,有四个受灾地区需要救援,分别是X1,X2,X3,X4。某救援部门考虑对其中一个灾情最严重的地区进行救援,需要通过专家对这四个备选受灾地区的情况进行打分进行应急决策,选出最为合理的施救地区。打分时主要考虑以上5个指标,分别是受灾人员的身体素质, 年龄、性别、身体健康状况等因素(I1)(满分150),受灾人员伤残情况(I2)(满分15),受灾人员的被困环境(I3)(满分15),受灾人数(人)(I4)以及受困时间 (小时)(I5)。在这五个指标中,I1,I2,I3可以看作效益型指标,I4和I5看作成本型指标。这四种方案的评价指标值如下所示:
步骤1 根据理想区间灰数的定义,得到指标的理想区间灰数分别为:
得到理想属性偏离度矩阵

步骤2 得到信息结构映像序列矩阵

步骤3 根据矩阵Y=(yij)m×n得到指标Ij的不确信度:
DOI(I1)=0.222,DOI(I2)=0.114,DOI(I3)=0.229,DOI(I4)=0.127,DOI(I5)=0.092
步骤4 根据信息结构映像序列矩阵和指标Ij的不确信度得到实质不确定因子矩阵:
步骤5 根据式(2)进行证据信息融合,得到:
CFT(h1/e1,e2,e3,e4,e5)=0.892,CFT(h2/e1,e2,e3,e4,e5)=0.828,
CFT(h3/e1,e2,e3,e4,e5)=0.847,CFT(h4/e1,e2,e3,e4,e5)=0.473。
步骤6 根据实质不确定因子最大化原则,受灾地区X1情况最好,受灾地区X4灾情最严重。故决策方案是该单位应该先去救助灾情最严重的地区X4。
为了更清晰的体现该方法的特点,以下与传统的线性加权方法进行对比分析。传统线性加权方法的思路是首选对各个属性进行规范化处理[13],然后计算出指标的权重,再进行区间灰数的线性加权,最后根据可能度进行择优排序。
首先对指标进行规范化处理,得到标准化决策矩阵

采用灰色关联方法得到权重w1=0.185,w2=0.21,w3=0.183,w4=0.207;w5=0.215;根据区间灰数的运算法则进行线性加权,得到方案Xi的综合评价值分别为
Z(X1)=[0.63,0.87],Z(X2)=[0.58,0.82],Z(X3)=[0.65,0.88],Z(X4)=[0.56,0.72]

对比分析表明:本文提出的方法在最终决策结果上与传统线性加权的方法相一致。但是本文所给决策方法的思想是根据证据推理获得方案的排序,更加符合人们应对突发事件进行应急决策的动态思考的特征;同时,在运算上采用了非线性的信息集合方式,在分辨效果上也好于传统的线性加权方法。
3 结论
对于突发性事件处置中的应急决策,由于决策者获得的信息往往是不完备、灰色或者模糊的,并且决策者所获得的信息随着灾情的演化而不断变化,这使得决策者做出科学的决策变得困难。本文提出了一种新的“证据推理决策”方法,即利用个体的经验和所能收集到的相关事实与数据作为判断与推理的证据进行证据推理和决策,找出最优方案;建立了基于证据推理的应急决策方法,给出了区间灰数决策方法步骤;通过案例分析可以看出该方法计算简单、使用方便并且推理效果好,能很好的适合突发事件应对中的快速应急决策问题。
[1] Zadah L A. Fuzzy sets[J]. Information and Control, 1965,8: 338-353.
[2] Chen S J, Hwang C L. Fuzzy multiple attribute decision making: methods and applications[M]. New York: Springer, 1992.
[3] 徐泽水.一种新的不确定性多属性决策方法[J].系统工程学报,2002,17(2): 177-181.
[4] Fan Z P, Ma J, Zhang Q. An approach to multiple attribute decision making based on fuzzy preference information alternatives[J]. Fuzzy Sets and Systems, 2002, 131: 101-106.
[5] Moore R E. Methods and application of Interval analysis[M]. London: Prentice Hall, 1979: 260-290.
[6] Tanaka H, Ukuda T, Asal K. On fuzzy mathematical programming[J]. Journal of Cybernetics, 1984,3: 37- 46.
[7] Ishibuchi H, Tanaka H. Multi-objective programming in optimization of the interval objective function[J]. European Journal of Operational Research, 1990, 48: 219-225.
[8] 徐泽水,达庆利.区间数排序的可能度法及其应用[J].系统工程学报,2003,18(1):67-70.
[9] Sengupta A, Pal T K. On comparing interval numbers[J]. European Journal of Operational Research, 2000, 127: 28- 43.
[10] Sengupta A, Pal T K, Chakraborty D. Interpretation of inequality constraints involving interval coefficients and a solution to interval linear programming[J]. Fuzzy Sets and Systems, 2001, 119: 129-138.
[11] Deng J L. The control problem of grey systems[J]. System & Control Letters, 1982, 1(5): 288-294.
[12] Liu S F, Lin Y. Grey information theory and practical applications[M]. London: Springer-Verlag, 2006.
[13] 刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].3版,北京:科学出版社,2004.
[14] 罗党.一类灰色区间聚类决策算法[J].郑州大学学报:理学版,2007,39(1):119-124.
[15] 党耀国,刘思峰,刘斌.基于区间数的多指标灰靶决策模型的研究[J].中国工程科学,2005,7(8):31-35.
[16] Shafer G..A Mathematical theory of evidence[M]. NH: Princeton University Press,1976.
[17] 王育红,党耀国.基于灰色关联系数和D-S证据理论的区间数投资决策方法[J].系统工程理论与实践,2009,29(11):128-134.
[18] 刘付显,邢清华.基于D-S融合证据的决策新方法[J].系统工程理论与实践,2009,29(7):125-131.
[19] 张岐山.灰朦胧集的差异信息理论[M].北京:石油工业出版社,2002.
[20] 张文修,梁怡,徐萍.基于包含度的不确定推理[M].清华大学出版社,2007.
[21] Mostaghimi M. Bayes estimation of a decision using information theory[J]. IEEE Transactions on Systems, Man, and Cybernetics(Part A: Systems and Humans), 1997, 27(4): 506-517.
Interval Grey Numbers Emergency Decision-making Methods Based on MYCIN Uncertainty Factor
JIANG Feng-guang1,3, LI Peng2, CHEN Li-wen1
(1.CollegeofEconomics&Management,HebeiUniversityofTechnology,Tianjin300401,China; 2.CollegeofEconomics&Management,JiangsuUniversityofScienceandTechnology,Zhenjiang212003,China; 3.CollegeofEconomics&Management,TianjinVocationalInstitute,Tianjin300410,China)
This paper focuses mainly on emergency decision-making problems when attribute values of corresponding alternatives are interval grey numbers. The MYCIN certainty factor is integrated into grey decision-making theory. By computing the certainty factor of all alternatives in different indices and fusion of them, the best alternative is obtained. Emergency decision-making method based on evidence reasoning is established and the procedure of interval grey numbers decision-making is presented. Finally,an example is given to illustrate the efficiency of the approach proposed in this paper.
interval grey numbers; MYCIN certainty factor; data fusion; emergency decision-making
2013- 05-16
河北省高等学校自然科学青年基金项目(2011111)
蒋风光(1971-)男,山东阳信人,博士生,研究方向:技术经济,金融风险。
N941.5
A
1007-3221(2015)04- 0030- 06

